Сивохин А.В. Мещеряков Б.К. Решение задач оптимального управления с использованием matlab и simulink
Подождите немного. Документ загружается.

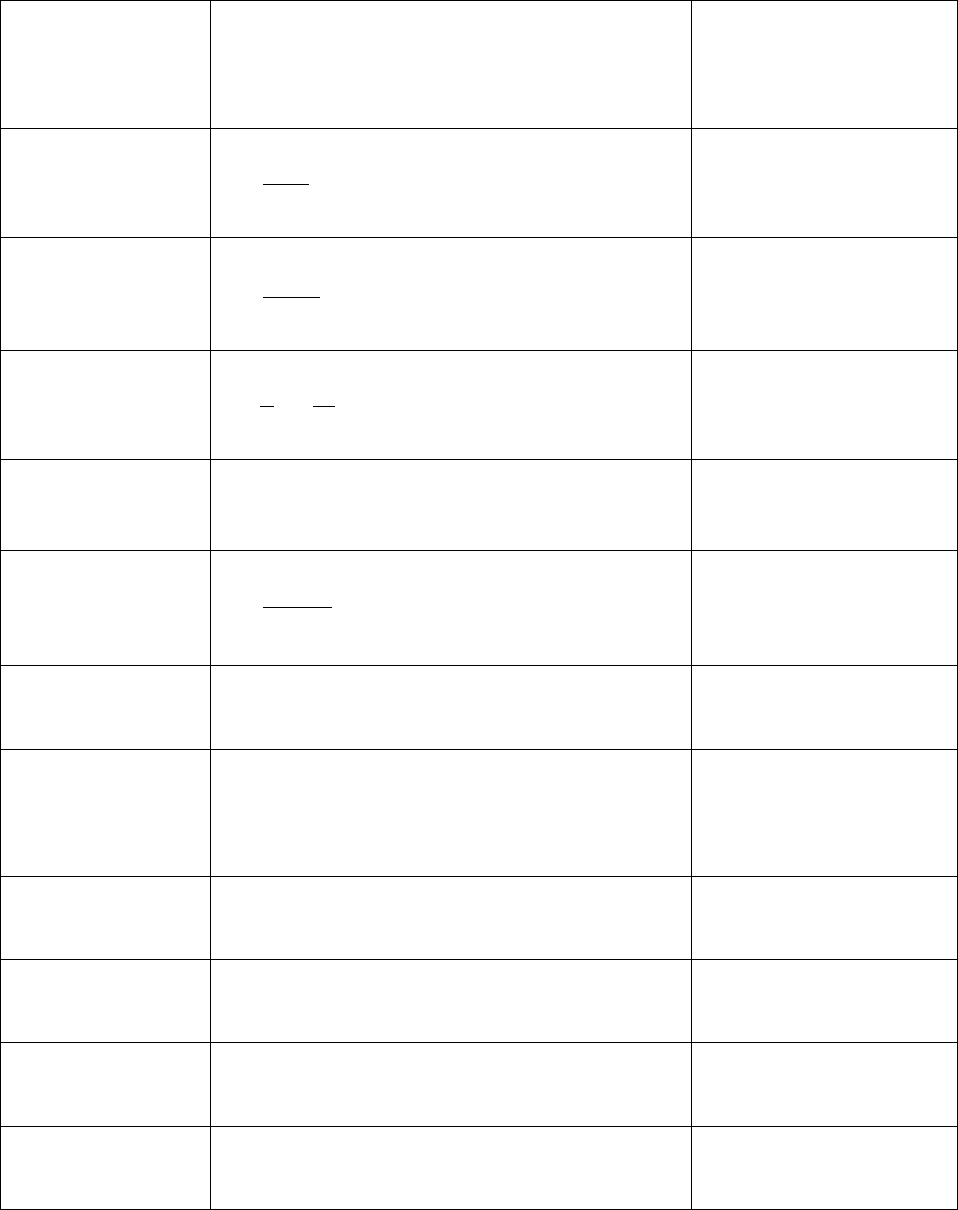
Таблица 3.1
Варианты описаний динамических систем
Номер
варианта
Варианты уравнений или их систем Начальные условия
1
1
1
'
+
−
=
t
x
x
x
(1) = 0
2
tx
x
x
2
1
'
+
=
x
(2) = 1
3
3
23
'
t
x
t
x =+
x
(1) = 3
4
2
2
22'
t
etxtx
−
=+
x
(0) = 1
5
22
2
'
xt
tx
x
+
=
x
(1) = 2
6
1'''
23
=+ xtxt
x
(1) = 1,
x
(e) = 0
7
3
'2'' txxx =+−
x
(0) = 24,
x
(1) =
7
8
t
exxx =+− 2'3''
x
(0) = 1,
x
(1) = 0
9
212211
23';2' xxxxxx
−
=
−=
1
x (0) = 1,
2
x (0) = 0
10
212211
2',24' xxxxxx
+
−
=
+=
1
x (0) = 2,
2
x (0) = 1
11
tt
exxxexxx 92',4025'
212211
−=+−=−+
1
x
(0) = 2,
2
x
(0) = 1

В качестве примера краевой задачи можно назвать задачу об изгибе
балки, жестко заделанной в точке
0
=
x и свободной в точке 1=x .
Следует заметить, что решение краевых задач значительно сложнее
решения задач Коши за исключением тех случаев, когда в распоряжении
исследователей имеется точное решение с произвольными константами,
которые остается выбрать для удовлетворения краевых условий. В
самом деле, при исследовании задачи Коши заданы все условия для
приближенного построения решения; так, например, для системы
);,,(
211
1
txxf
dt
dx
=
);,,(
212
2
txxf
dt
dx
=
(3.6)
мы знаем
2010
, xx и, следовательно,
0
1
dt
dx
и
0
2
dt
dx
. Поэтому у нас хватает
данных для построения интегральной кривой хотя бы путем стыкования
кусков касательных. Если же для той же системы заданы
1001
)( xtx
=
10
tt
<
,
2112
)( xtx
=
(3.7)
то данных для приближенного построения решения в точке
0
tt
=
не
хватает, ибо мы непосредственно не может использовать значения )(
12
tx .
Вопросы существования и единственности решения краевых задач
решаются много сложнее, чем аналогичные вопросы для задачи Коши
даже в случае линейного уравнения.
Если при составлении уравнений принимаются во внимание все
факторы, влияющие на динамическую систему, то уравнения (3.1)
получаются сложными, по большей части нелинейными и трудно
поддающиеся решению. Для качественного исследования таких
систем
уравнения отдельных элементов (звеньев) заменяют приближенными к
ним линейными дифференциальными уравнениями с постоянными
коэффициентами. Такое преобразование системы уравнений называется
ее линеаризацией. На вопрос, в какой мере и при каких условиях
допустима такая линеаризация уравнений, отвечают теоремы об
устойчивости линеаризованных систем [4].
Линеаризованную систему можно легко привести к одной функции
)(tx и записать в операторной форме:

)()()()( tupUtxpD
=
.
(3.8)
В этом уравнении
dt
d
p =
– оператор дифференцирования, а )( pD и
)( pU
- операторные полиномы с постоянными коэффициентами.
Как известно из теории дифференциальных уравнений, общее
решение
)(tx уравнения (3.8) находится как сумма двух решений )(tx
c
и
)(tx
b
:
)()()( txtxtx
bc
+
=
(3.9)
где
)(tx
c
– общее решение однородного уравнения
,0)()(
=
txpD
c
(3.10)
а
)(tx
b
– частное решение заданного уравнения
)()()()( tupUtxpD
b
=
(3.11)
Движение системы, определяемое составляющей
)(tx
c
, называется
свободным движением, а составляющей
)(tx
b
– вынужденным
движением.
Общее решение однородного уравнения
(3.1) )(tx
c
состоит из суммы
слагаемых, каждое из которых отвечает корню или группе корней
характеристического уравнения
.0)(
=
pD
(3.12)
Вид слагаемого зависит от типа корня или группы корней следующим
образом:
а) каждому значению вещественного корня
k
pp
=
отвечает слагаемое
вида
tp
k
k
eС
(3.13)
где
k
С – постоянная интегрирования;
б) каждой группе из s вещественных кратных корней отвечает
слагаемое вида
tp
s
s
k
etCtCC )...(
1
21
−
+++
(3.14)
где
s
CCCC ,...,,,
321
– постоянные интегрирования;
в) каждой паре комплексных сопряженных корней
kk
i
β
α
± отвечает
слагаемое вида
)sincos( tDtCe
kkkk
t
k
ββ
α
+
(3.15)
где
k
C и
k
D – постоянные интегрирования;
г) каждой группе из s комплексных сопряженных кратных корней
отвечает слагаемое вида
]sin)...()...[(
1
21
1
21
ttDtDDtctCtCCe
k
s
sk
s
s
t
k
ββ
α
−
−
+++++++
(3.16)
где
i
C и
i
D – постоянные интегрирования.
Число постоянных интегрирования во всех случаях должно быть
равно порядку дифференциального уравнения (3.8). Они определяются
из начальных условий движения системы регулирования, в качестве
которых принимают значения
c
x и всех её производных до (n-1)-го
порядка включительно в начальный момент времени t = 0 согласно
теореме Коши.
Свободное движение системы
)()()()( txtxtxtx
bcпер
−
=
=
(3.17)
определяет переходной процесс регулирования, который имеет большое
значение для работы системы.
В зависимости от значений корней характеристического уравнения
могут иметь место следующие виды переходного процесса.
1.Один из вещественных корней положительный. Соответствующее
этому корню слагаемое
tp
k
k
eС
с течением времени неограниченно
возрастает, в результате чего
∞
→
пер
x
при
∞
→t . Такой переходной
процесс называется неустойчивым.
2.Вещественная часть одной пары комплексных сопряженных корней
положительна. Соответствующее этим корням слагаемое
)sincos( tDtCe
kkkk
t
k
ββ
α
+ определяет периодические колебания с
неограниченно возрастающей амплитудой. Такой переходной процесс
также называется неустойчивым.
3.Все вещественные корни, а также вещественные части комплексных
сопряженных корней отрицательны. В этом случае все оставляющие, как
нетрудно убедится, с течением времени стремятся к нулю, и
∞
→
пер
x при
∞→t . Переходный процесс называется устойчивым, или затухающим.
При этом различают затухание апериодическое, когда оно происходит
без колебаний, и колебательное, когда затухающая составляющая
совершает периодические колебания с амплитудой, стремящейся к
нулю.
4.Один из вещественных корней равен нулю. В этом случае в составе
пер
x
появляется постоянное слагаемое.
5.Пара комплексных сопряженных корней имеет нулевую
вещественную часть. В этом случае
пер
x будет содержать слагаемое,
представляющее колебательное движение с постоянной амплитудой.
Такие колебания называются не затухающими.
6.Имеются кратные нулевые корни и кратные чисто мнимые корни. В
этом случае переходной процесс неустойчив, так как одно из слагаемых
пер
x будет неограниченно возрастать апериодически или в виде
колебаний с возрастающей амплитудой.
3.2 Разработка аналитических моделей
Рассмотрим пример динамической системы. Пусть
дифференциальное уравнение, которое описывает ее поведение, имеет
вид:
t
exxx
4
3'2'' =−−
, 1)0(
=
x 0)0(' =x .
(3.18)
Перепишем уравнение так:
t
exxx
4
3'2'' =−− .
(3.19)

Найдем отображения функции и ее производных по таблице или с
помощью функции laplace системы MATLAB:
)( pXx →
;
)0()(' xppXx
−
→ ;
);0(')0()(''
2
xpxpXpx −−→
4
1
4
−
→
p
e
t
;
(3.20)
1)('
−
→ ppXx ;
.)(''
2
ppXpx −→
Подставим в уравнение(3.19) и выполним преобразования:
4
1
)(3)1)((2)(
2
−
=−−−−
p
pXppXppXp
;
4
1
)(32)(2)(
2
−
=−+−−
p
pXppXppXp
;
(3.21)
1)4)((3)4(2)4)((2)4()4)((
2
=−−−+−−−−− ppXppppXppppXp ;
)4(2)4(1)32)(4)((
2
−−−+=−−− pppppppX ;
96)32)(4)((
22
+−=−−− ppppppX .
В результате получаем:
)1)(4(
)3(
)3)(1)(4(
)3(
)32)(4(
96
)(
2
2
2
+−
−
=
−+−
−
=
−−−
+−
=
pp
p
ppp
p
ppp
pp
pX
.
(3.22)
Разложим на простейшие дроби:
)1)(4(
)4()1(
14)1)(4(
)3(
+−
−
+
+
=
+
+
−
=
+−
−
pp
pBpA
p
B
p
A
pp
p
.
(3.23)
Пусть
1−=p , тогда
45
−
=
− B
;
5
4
=B
.
Пусть
4=p , тогда 15 =A ;
5
1
=A .
Находим отображение функции
)(tx :
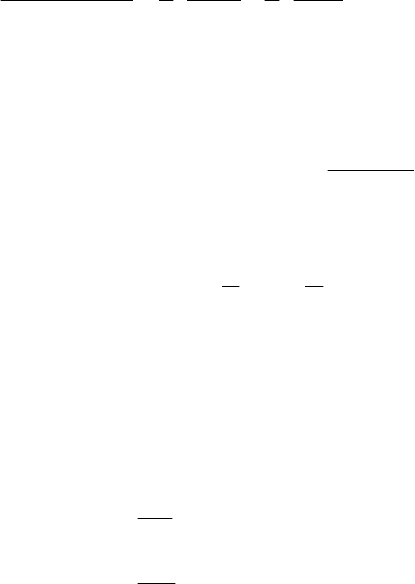
1
1
5
4
4
1
5
1
)1)(4(
)3(
)(
+
⋅+
−
⋅=
+−
−
=
pppp
p
pX
.
(3.24)
Перейдем к оригиналу. Так как
α
α
−
→
p
e
t
1
, то
tt
eetx
−
+=
5
4
5
1
)(
4
.
(3.25)
Рассмотрим еще один пример, когда динамика описывается
системой дифференциальных уравнений следующего вида:
⎪
⎪
⎩
⎪
⎪
⎨
⎧
+=
+=
21
2
21
1
2
2
xx
dt
dx
xx
dt
dx
,
(3.26)
1)0(
1
=
x
,
3)0(
2
=
x .
Перепишем систему так:
⎩
⎨
⎧
+=
+=
212
211
2'
2'
xxx
xxx
.
(3.27)
Перейдем к отображениям:
)(1
1
pXx → ;
)(2
2
pXx →
;
)0()(1'
11
xppXx
−
→ ;
(3.28)
)0()(2'
22
xppXx
−
→
;
1)(1'
1
−
→ ppXx ;
3)(2'
2
−
→ ppXx .
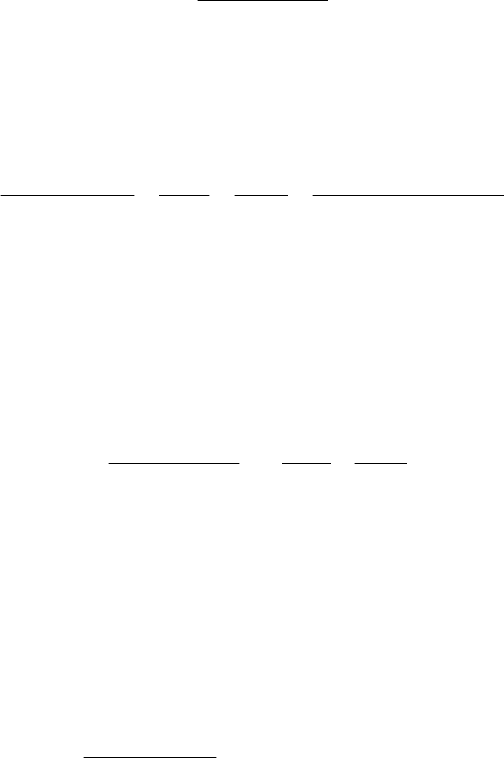
Подставляем в (3.27):
⎩
⎨
⎧
+=−
+=−
);(22)(13)(2
);(2)(121)(1
pXpXppX
pXpXppX
(3.29)
⎩
⎨
⎧
=−+−
=−−
;3)(2)2()(1
;1)(2)(1)2(
pXppX
pXpXp
.
(3.30)
Умножим первое уравнение на
)2(
−
p
и сложим уравнения:
;32)(1)1)2((
2
+−=−− ppXp
;1)(1)34(
2
+=+− ppXpp
(3.31)
)3)(1(
1
)(1
−−
+
=
pp
p
pX .
Разложим на простейшие дроби:
)3)(1(
)1()3(
31)3)(1(
1
−−
−+
−
=
−
+
−
=
−−
+
pp
pBpA
p
B
p
A
pp
p
.
(3.32)
Пусть
1=p
, тогда
22
=
−
A
,
1
−
=
A
.
Пусть
3=p , тогда 42
=
B
, 2
=
B
.
3
2
1
1
)3)(1(
1
)(1
−
+
−
−=
−−
+
=
pppp
p
pX .
(3.33)
Отображение для
)(
1
tx
найдено. Теперь можем найти оригинал по
таблицам[5]:
tt
eetx −=
3
1
2)(
.
Найдем
)(2 pX . Подставим )(1 pX в первое уравнение системы (3.30):
)(21
)3)(1(
)1)(2(
pX
pp
pp
=−
−−
+
−
.
(3.34)
Приведем к общему знаменателю:

)3)(1(
53
)(2
−−
−
=
pp
p
pX .
(3.35)
Разложим на простейшие дроби:
)3)(1(
)1()3(
31)3)(1(
53
−−
−
+
−
=
−
+
−
=
−−
−
pp
pBpA
p
B
p
A
pp
p
.
(3.36)
Пусть
1=p , тогда 12
−
=
−
A
; 1
=
A
.
Пусть
3=p
, тогда
42 =
B
;
2
=
B
и отображение запишется следующим
образом:
3
2
1
1
)3)(1(
53
)(2
−
+
−
=
−−
−
=
pppp
p
pX .
(3.37)
Тогда оригинал равен
tt
eetx
3
2
2)( +=
.
(3.38)
3.3 Программная реализация аналитических моделей
function [X,DX,D2X] = DSolveXDXD2X
%-- ФУНКЦИЯ ДЛЯ НАХОЖДЕНИЯ X(t)
%-- И ЕЕ ПРОИЗВОДНЫХ DX(t) и D2X(t):
%-- 1.Нахождение X(t):
syms x t
X = dsolve('D2x-2*Dx-3*x=exp(4*t)','x(0)=1','Dx(0)=0');
%-- 2.Нахождение DX(t):
DX = diff(X);
%-- 3.Нахождение D2X(t):
D2X = diff(DX);
%-- 4.Векторизация и подстановка X,DX,D2X и t:
X = vectorize(X)
X = subs(X,{t},{0:0.1:1});
DX = vectorize(DX);
DX = subs(DX,{t},{0:0.1:1});
D2X = vectorize(D2X);
D2X = subs(D2X,{t},{0:0.1:1})
t = 0:0.1:1;
%-- 5.Визуализация U(t):
U = exp(4.*t);
subplot(4,2,1)
plot(t,U,'r')
xlabel('t')
ylabel('U')
%-- 6.Визуализация X(t):
subplot(4,2,3)
plot(t,X,'r')
xlabel('t')
ylabel('X')
%-- 7.Визуализация DX(t):
subplot(4,2,2)
plot(t,DX,'r')
xlabel('t')
ylabel('DX')
%-- 8.Визуализация D2X(t):
subplot(4,2,4)
plot(t,D2X,'r')
xlabel('t')
ylabel('D2X')
%-- 9.Конец функции DSolveXDXD2X
function [X,DX,D2X] = EvalXDXD2X
%-- ФУНКЦИЯ ДЛЯ ВЫЧИСЕНИЯ ЗНАЧЕНИЙ U(t),X(t) =
%-- 1/5e(4t)+4/5e(-t) И ЕЕ ПРОИЗВОДНЫХ:
%-- 1.Задание вектора t:
t = 0:0.1:1;
%-- 2.Вычисление U(t):
U = exp(4.*t);
%-- 3.Вычисление X(t):
X = 1./5.*exp(4.*t)+4./5.*exp(-t);
%-- 4.Вычисление DX(t):
DX = 4./5.*exp(4.*t)-4./5.*exp(-t);
%-- 5.Вычисление D2X(t):
D2X = 16./5.*exp(4.*t)+4./5.*exp(-t);
%-- 6.Визуализация U(t):
subplot(4,2,1)
plot(t,U,'r')
xlabel('t')
ylabel('U')
%-- 7.Визуализация X(t):
subplot(4,2,3)
plot(t,X,'r')
