Ситник В.Ф. Системи підтримки прийняття рішень

Подождите немного. Документ загружается.

ми. Ключовою величиною в цій моделі є бета — міра

чутливості прибутку щодо інвестицій на ринку. Бета є

відношенням середнього квадратичного відхилення багато

диверсифікованого портфеля активів до середнього

квадратичного відхилення ринкового портфеля. Принцип бети

пов'язаний з принципом преміювання за ризик, тобто, з

додатковою винагородою, яка має пропонуватися інвесторам,

щоб спонукати їх брати на себе ризик, який асоціюється з

даною інвестицією. Ризики виражаються в термінах щорічних

коефіцієнтів окупності.

Мова фінансового моделювання IFPS дає змогу створювати

моделі для визначення необхідного коефіцієнта окупності

інвестиції та бети за іншими величинами. В ній передбачені

можливості розширення принципу бети до регульованих

інвестицій, тобто, інвестицій, в яких дробова частина капіталу

одержується за допомогою позики.

Аналіз фінансового стану. Моделі IFPS містять більшість

уживаних для аналізу фінансового стану відношень, зокрема,

три типи показників: показники лівериджу (leverage), тобто

впливу, ліквідності та ефективності.

Модель управління готівкою. Управління балансом готівки

на фірмі може моделюватися в термінах теорії запасів. Фірми

взагалі дотримуються правила, щоб мати мінімальну кількість

готівки напоготові з метою виконання повсякденних справ. Ця

кількість інколи визначається вимогами, нав'язаними фірмам

банками. Існує також обмеження щодо максимально бажаної

кількості готівки. Цей максимум відображає компроміс між

вкладенням грошей у ліквідні інвестиції, як наприклад у

федеральні скарбничі векселі, і вартістю втрачених процентів

через те, що готівка не вкладається в справу. Можна вважати,

що готівка подібна до будь-якого іншого ресурсу, який

компанія тримає в товарно-матеріальних запасах.

В IFPS/ Plus для обчислення раціональної кількості готівки

застосовується модель Міллера—Oppa (Miller—Orr). Модель

допускає, що ви знаєте мінімально потрібний касовий баланс,

дисперсію щоденних оплат готівкою, щоденну процентну

ставку і вартість транзакції для кожного продажу або купівлі

цінних паперів.

Формальні моделі фінансового прогнозування. В IFPS міс-

титься узагальнена фінансова модель прогнозування, яка дає

змогу створювати прогнози про доходи (прибутки і збитки);

про джерела надходження і використання грошових фондів;

балансових звітів на таку кількість років, яку ви бажаєте.

159

Додатки щодо статистики

Статистичні методи потрібні для розв'язування бага-

тьох проблем: у фінансах, торгівлі, обліку, економіці й інших

сферах. У системі IFPS/Plus через здатність подавати

інформацію в матричному вигляді і можливість проведення

аналізу типу «ЩО ..., ЯКЩО...?» легко можна здійснювати

різні статистичні обчислення і аналізи, зокрема, обчислювати

середню величину, дисперсію, середнє квадратичне

відхилення, медіану та інші параметри розсіювання, довірчі

інтервали, оцінювати розподіли ймовірностей, аналізувати

часові ряди, здійснювати прогнозування тощо.

Додатки стосовно виробництва і

оперативного управління

Засоби IFPS/Plus можна продуктивно застосовувати

до проблем у виробництві та оперативному управлінні (В/ОУ).

Сфери виробництва і управління виробництвом стали

виключно важливими в останні роки у всьому світі, оскільки

конкуренція робить удосконалення стосовно продуктивності

необхідними для виживання. Велика кількість методів

управління включає фінансовий аналіз і тому В/ОУ може бути

добре модельованим в IFPS/Plus, зокрема, щодо завдань

аналізу беззбитковості, створення агрегованих календарних

планів, управління товарно-виробничими запасами тощо.

4.3.7. Імітаційне моделювання

(аналіз ризику) у Visual IFPS/Plus

Загальний опис і концепція

У створюваних засобами IFPS/Plus моделях,

уважало-ся, що всі початкові дані і всі зв'язки точно відомі.

Такі моделі називають детермінованими. Хоч це часто (але не

завжди) буває так, але маючи статистичну інформацію,

наприклад результати бухгалтерського обліку, ставиться

завдання зробити оцінювання майбутнього за допомогою цих

моделей. Майбутнє є сумнівним і тому ризикованим з

бізнесового погляду. За створення ділових рішень ці ризики

мають бути оціненими. Інакше кажучи, виникає проблема

прийняття рішень за умов ризику, коли параметри і

160

змінні задачі є випадковими величинами (наприклад,

собівартість продукції, частку ринку, загальний збут у

майбутніх періодах не можна визначити точно). Якщо це так,

то чи буде ризикований захід прибутковим? У СППР Visual

IFPS/Plus є три шляхи дослідження аспектів ризикованості

(невпевненості).

Перший шлях полягає у використанні аналітичних

можливостей IFPS/Plus: WHAT IF (Що..., Якщо...?), GOAL

SEEKING (Пошук Мети) і VARIANCE (Коливання). Ці опції

дають змогу дослідити альтернативні ситуації за допомогою

модифікування моделі й визначити впливи змін. Хоч такий

підхід і придатний для дослідження впливів змін однієї чи

двох змінних або отримання специфічної відповіді, що

базується на припущеннях вищого керівництва, ці три

можливості не є найефективнішими для аналізу ризику.

Другий шлях — зробити оцінювання найкращого і

найгіршого випадків. За цього підходу оцінки створюються з

урахуванням сприятливіших і найнесприятливіших умов, які

кожна вхідна змінна могла б мати. Для найкращого випадку

встановлюють оптимістичні значення, а для найгіршого —

песимістичні. У реальному світі не всі змінні одночасно

набувають своїх найкращих значень, як і найгірших. Хоч

дослідження критичних ситуацій дуже корисне, але цей підхід

не виводить на сукупність ситуацій, які можуть реально

очікуватися.

Третій шлях — використовувати імітаційне моделювання

(машинну імітацію) або, як це названо в IFPS/Plus, симуляцію

Монте-Карло (Simulation Monte Carlo). Зауважимо, що в

україномовній літературі з дослідження операцій частіше

застосовується синонім терміна «симуляція» — імітація.

Користувачі даної СППР мають зрозуміти відмінність між

поняттями «моделювання» (Modeling) і «симуляція»

(Simulation). Моделювання і симуляція (або імітація)

відрізняються бо:

• моделювання — це аналітичне дослідження, яке включає

формування ситуації у вигляді математичних відношень;

• імітація — експериментальне дослідження, оскільки

воно включає виконання вибіркових машинних експериментів

на моделі ситуації.

Ключовими словами в цьому визначенні імітації є

«вибіркові експерименти». У вибірковому експерименті

створюється великий ряд випробувань. Через наявність

невпевненості наслідок кожного випробування може

відрізнятися від наслідків інших випробувань. За імітації

вибіркові експерименти виконуються на комп'ютерній моделі,

даючи змогу в такий спосіб зробити багато

161

випробувань з незначними матеріальними витратами (на відміну від

проведення натурних експериментів).

Розв'язуючи задачу, яка містить одну або більше випадкових

змінних, необхідно мати правило для вирішення того, яких значень

набуватиме кожна випадкова змінна. Найефективніший шлях для

цього — присвоїти значення відповідно до розподілу ймовірностей і

вважати їх значеннями, що нібито насправді мали місце. Оскільки

за імітації реалізується вибірковий експеримент, то цей процес

повторюється багато разів (наприклад, 1000 разів). Кожного разу,

коли звертаємося до випадкової змінної, то вибираємо значення з

розподілу ймовірностей і використовуємо його для визначення

наслідку, тобто вибираємо значення випадкової змінної так, щоб

частота входження окремих значень була пов'язана з розподілом

імовірностей.

Процедура імітації в короткому викладі складається з таких

кроків:

1. Побудуйте імітаційну модель, яка визначає невпевненість і

ризики.

2. Виконайте вибіркові експерименти на комп'ютері, повто-

рюючи розв'язання за моделлю велику кількість разів. Кожного разу

отримаєте один можливий сценарій.

3. Проведіть статистичні аналізи наслідків експериментів.

4. Використовуйте одержані статистичні результати для при-

йняття рішення.

Після дослідження результатів можна провести додаткові роз-

в'язування задачі за моделлю, щоб краще підсилити статистичну

точність результатів, або зупинитися на певному дотягненому ре-

зультаті, прийнявши потрібні рішення, грунтуючись на отриманих

результатах. Докладнішу інформацію щодо імітаційного мо-

делювання можна знайти в навчальному посібнику: Ситник В. Ф.,

Орленко Н. С. Імітаційне моделювання. — К.: КНЕУ, 1998. — 232 с.

Підходи до імітації в IFPS/Plus

IFPS/Plus забезпечує можливість виконання імітації за

методом Монте-Карло. При цьому потрібно описати розподіл

ймовірностей кожної випадкової величини. Коли викликається

команда MONTE CARLO, то система IFPS/Plus розв'язує задачу за

моделлю багато разів з різними комбінаціями значень величин, що

кожного разу вибираються з відповідних розподілів ймовірно-стей,

які перед цим були конкретизовані. Результати

162

цих експериментів статистично аналізуються в СППР і на

виході отримуємо статистичні результати. Ці результати

можна інтерпретувати як ризики, включені у рішення.

Наприклад, можна дізнатися, що є шанс на 10 %, що

внутрішній коефіцієнт окупності перевищить 25 % , або з

імовірністю 0,9 можна запевняти, що він перевищить 14 %.

Якщо в IFPS/Plus досліджували детерміновану модель і ді-

йшли висновку, що необхідно змінити основну структуру

моделі, щоб включити аналіз ризику, то потрібно лише задати

специфічні параметри з їх імовірностями, а не окремі точкові

значення. IFPS/Plus містить чотири розподіли ймовірностей, а

також можна імітувати будь-який нагромаджений розподіл.

До того ж IFPS/Plus здатна генерувати сценарії, що

грунтуються на присвоєнні високого, низького, середнього і

найімовірнішого значень випадкових змінних.

Вбудовані розподіли імовірностей

В IFPS/Plus вбудовані такі розподіли ймовірностей:

1.Однорідний (рівномірний) розподіл UNIRAND.

2.Трикутний розподіл TRIRAND.

3.T1090RAND — альтернативний вид трикутного

розподілу.

4. Нормальний розподіл NORRAND.

Крім того система дає змогу моделювати будь-який

розподіл за допомогою операторів GENRAND і CUMRAND.

Для кожного з цих розподілів імовірностей потрібно

конкретизувати його ім'я та два або більше їх параметрів.

Наприклад, UNIRAND (10,30) означає рівномірно розподілені

ймовірності на інтервалі значень змінної від 10 до 30. Щоб

генерувати в IFPS/Plus довільні значення цього розподілу,

потрібно написати, наприклад, COST-UNIRAND (10,30).

У разі моделювання з багатьма повтореннями кожного разу

IFPS/Plus вибирає довільне значення між 10 і 30. Узагалі,

розподіл UNIRAND конкретизується двома параметрами:

верхнім і нижнім значеннями змінної.

Отримання рівномірно розподіленої на відрізку [0,1]

величини RANDON NUMBER (яка в зазначеному вище

посібнику позначена символом £) відбувається за допомогою

твердження: RANDON NUMBER = UNIRAND (0,1).

Випадкова величина RANDON NUMBER може

використовуватися для генерування довільного розподілу

ймовірностей. Наприклад, імітація RANDON INTEGER

163

— випадкових рівномірно розподілених чисел 0, 1, ..., 9

виконується за допомогою виразу: RANDON

INTEGER=TRUNCATE(10* RANDON NUMBER), де TRUN-

CATE — вбудована в IFPS/Plus математична функція взяття

цілої частини числа.

У разі імітації задач з масового обслуговування часто

використовується експоненціальний розподіл. Генерування

випадкової, експоненціально розподіленої величини

EXPRANDON, математичне сподівання якої дорівнює М,

відбувається за допомогою такого виразу: EXPRANDON = -

M*NATLOG(RANDON NUMBER), де NATLOG — вбудована

в IFPS/Plus математична функція обчислення натурального

логарифма.

Трикутний розподіл імовірностей (TRIRAND і

T1090RAND) є особливо корисним у разі імітації ризику. Для

його застосування необхідно задати три параметри: нижню

межу; найімовірніше значення (максимальне значення

щільності розподілу в цій точці); верхню межу (висота

трикутника вибирається з умови, що його площа дорівнює

одиниці). Трикутний розподіл є зручною апроксимацією

розподілів, коли область можливих значень (наприклад,

верхні й нижні обмеження) відома і розподіл має єдиний пік.

Це також надає можливість виразити ідею, що ризик

симетрично не розподіляється навколо певного значення.

Певним значенням трикутного розподілу є мода, а не середнє

значення величини.

Альтернативний шлях конкретизації трикутного розподілу

— використовувати функцію T1090RAND. Якщо ви не знаєте

точно найменше і найбільше значення, які може набувати

певна змінна, то ви можете оцінити десяти- і

дев'яностопроцентні точки на розподілі.

Щоб генерувати нормально розподілену випадкову змінну,

необхідно конкретизувати її середнє значення і середнє

квадратичне відхилення. Наприклад, NORRAND(100,10)

створює нормальний розподіл змінної з середнім значенням

100 і середнім квадратичним відхиленням 10. У мові

фінансового моделювання IFPS/Plus в основу вбудованого

нормального розподілу N0R-RAND покладений стандартний

підхід, що ґрунтується на використанні центральної граничної

теореми [37].

Визначення власних розподілів імовірностей

Хоч багато бізнесових ситуацій можуть бути

описані з використанням вбудованих розподілів імовірностей,

проте можуть бути випадки, де потрібно імітувати деякий

інший розподіл. У такому разі можна визначати або функцію

щільності GENRAND або нагромаджений розподіл

(інтегральну функцію розподілу) CUMRAND.

164

Застосування імітаційної моделі

Реалізація імітаційної моделі передбачає

багатократне її застосування, використовуючи різні комбінації

довільно вибраних значень за допомогою розподілів

імовірностей. Мета полягає в отримані інформації не тільки

щодо середньої величини (наприклад, яка очікується)

наслідку, але також стосовно розподілу ймовірностей

можливих результатів (щоб знати ризики).

Щоб почати процес пошуку розв'язку задачі,

використовується команда Monte Carlo замість команди Solve.

Ця команда має вираз: Monte Carlo number, де «number»

означає кількість виконуваних ітерацій. Якщо ви пропускаєте

number, то IFPS/Plus виконає 100 ітерацій (за замовчування).

Як тільки система перейшла в режим імітаційного моделю-

вання, потрібно вибрати та ввести в систему:

• змінні, які ви хочете зробити аналізованими;

• формат, який ви бажаєте для виведення даних

(наприклад, гістограма, частотний розподіл);

• стовпці (тобто, періоди), для яких ви хочете отримати на-

друковані результати.

Якщо при введенні опцій моделі Монте-Карло в систему

допущена помилка, то система передбачає певні варіанти її

виправлення.

Інтерпретація

результатів імітаційного

моделювання

Результати застосування моделі Monte-Carlo друку-

ються у форматі, який відрізняється від звичайного виведення

даних IFPS/Plus. Команда Solve закінчується електронною таб-

лицею, яка надає окреме значення для кожного ряду і стовпця,

конкретизованих в опціях Solve. Опції моделі Monte-Carlo

закінчуються одним або більше розподілами ймовірностей для

кожної змінної і певними стовпцями. Вихід Monte-Carlo

організовується в такій послідовності: таблиця нормальної

апроксимації, частотна таблиця, описова статистика (середнє

значення, середнє квадратичне відхилення, асиметрія,

крутизна та ін.), гістограма.

Після роздруковування результатів за необхідності можна

здійснити додаткові ітерації імітаційної моделі,

використовуючи спеціальну команду POOL. Наприклад, за

командою POOL 100 IFPS/Plus виконає 100 додаткових

ітерацій і потім надрукує результат для об'єднаних даних

після всіх виконаних ітерацій.

165

Приклад імітаційної моделі

Нехай середня за розміром хімічна фірма бажає

інвестувати 10 млн дол. у програму удосконалення головного

підприємства, сподіваючись, що ця програма матиме

життєвий цикл, який дорівнює десяти рокам [69]. Керівництво

фірми визначило, що ключовими факторами при аналізуванні

прибутковості цього запропонованого капіталовкладення є:

обсяг ринку (Market size); pea-лізаційна ціна (Selling price);

частка ринку компанії (The company's market share); загальні

інвестиції (Total investment); обсяг страхування інвестицій

(Salvage value of the investment); змінні (експлуатаційні)

витрати (Operating costs); постійні витрати (Fixed costs).

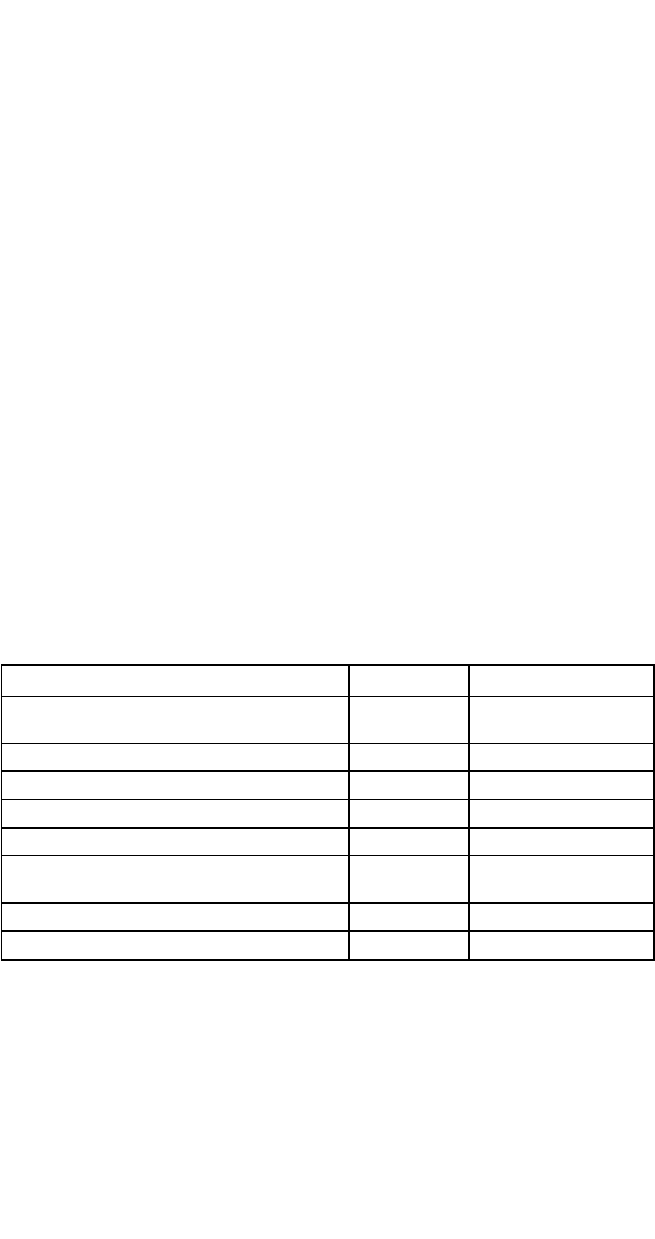
Усі ці показники пов'язані з невпевненістю, яка

моделюється розподілами ймовірностей, описаними у табл.

4.3. Дані таблиці свідчать про велику міру невпевненості, з

якою можна зустрітися. Формулюючи прогноз, компанія знає,

що має намір закрити об'єкт, якщо реа-лізаційна ціна буде

нижчою, ніж змінні витрати на одиницю продукції. У такому

разі необхідно сплатити постійні (фіксовані) витрати.

Таблиця 4.3

ФУНКЦІЇ РОЗПОДІЛУ ЙМОВІРНОСТЕЙ

ВИТРАТ І НАДХОДЖЕНЬ ХІМІЧНОЇ

ФІРМИ

Показник Розподіл Значення параметрів

Початковий обсяг ринку (Initial Market) трикутний 100 000, 250 000,

34 000

Ринкове зростання (Market Growth) трикутний 1, 1.03, 1.06

Реалізаційна ціна (Selling Price) трикутний 385,510,575

Частка ринку (Market Share) однорідний 12% до 17%

Інвестиція (Investment), млн дол. трикутний 7,9.5, 10.5

Змінні витрати на одиницю продукції

(Operating Cost per unit)

трикутний 370, 435, 545

Постійні витрати (Fixed Cost), $ тисячі трикутний 250, 300, 375

Обсяг страхування (Salvage Value) трикутний 3.5,4.5,5

На рис. 4.8 показана імітаційна модель IFPS/Plus для цієї

ситуації. Різні розподіли ймовірностей, наведені в табл. 4.3,

були вписані в модель. Запрограмовані також умови

припинення роботи. Умова зупинення виробництва

виражається за допомогою використання вбудованої функції

MAXIMUM для визначення доходу. Якщо реалізаційна ціна

нижча від експлуатаційних витрат, то дохід дорівнює 0; якщо

вища, то дохід визначається

166

множенням обсягу збуту на різницю між реалізаційною ціною

і змінними (експлуатаційними) витратами.

MODEL RISK VERSION OF 03/06/95 13:41

COLUMNS 1..10

MARKET = TRIRAND (100 000, 250 000, 340 000), PREVIOUS * TRIRAND

(1,1.03,1.06)

SELLING PRICE = TRIRAND(385,510,575)

MARKET SHARE = UNIRAND(.12,.17)

SALES VOLUME = MARKET * MARKET SHARE

INVESTMENT = TRIRAMD(7, 9.5,10.5) x 1000000,0

LIFE = 10

OPERATING COST = TRIRAND(370,435,545)

FIXED COST = TRIRAND(250, 300, 375) x 1000

REVENUE = MAXIMUM(0,(SELLING PRICE - OPERATING COST) х

SALES VOLUME)

NET INCOME = REVENUE - FIXED COST

SALVAGE VALUE = 0 FOR 9JRIRAND (3.5,4.5,5) x 1 000 000

RATE OF RETURN = IRR (NET INCOME + SALVAGE VALUE,

INVESTMENT)

Рис. 4.8. Імітаційна модель дослідження ризику

інвестування

Багато цінної інформації одержується тоді, коли за

допомогою команди MONTE CARLO 200 :

ENTER SOLVE OPTIONS

? monte carlo 200

ENTER MONTE CARLO OPTIONS

? hist net income

ENTER MONTE CARLO OPTIONS

? none система IFPS/Plus виконує 200 прогонів (ітерацій)

імітаційної моделі й видає результати у вигляді таблиці частот

(рис. 4.9), статистичних характеристик (рис. 4. 10), гістограми

розподілу чистого прибутку — NET INCOME (рис. 4.11) і

коефіцієнта окупності або норми прибутку — RATE OF

RETURN (рис. 4.12).

FREQUENCY TABLE

PROBABILITY OF VALUE BEING GREATER THAN INDICATED

90 80 70 60 50 40 30 20 10

NET INCOME 10 -315 -286 166 657 1213 1847 2698

3556 4951 *1000

RATE OF RETURN 10 -.120 -.110 -.57 .077 .075 .145 .226

.315 .429

Рис. 4.9. Результати імітаційного моделювання у вигляді

таблиці частот

167

SAMPLE STATISTICS

MEAN STD DEV SKEWNESS KURTOSIS 10PS CONF MEAN 90PS

NET INCOME

10 1772393 2056882 .9 2.9 1586225

1958560

RATE OF RETURN

10 .1144 .2128 .6 2.4. .0951 .1336

Рис. 4.10. Результати імітаційного

моделювання у вигляді статистичних

характеристик

10 OF NET INCOME

Аналізуючи результати імітаційного моделювання, можна

зазначити, що навіть 10-го року чистий дохід може сильно

коливатися (між збитками понад 300 тис. дол. і прибутком

понад 4 млн дол.). До того ж, коефіцієнт окупності змінюється

відповідно до цих показників інвестиції від -12,0 % до 42,9 % і

тільки з меншою ймовірністю ніж 0,4 він може перевищити 15

168