Сиротин С.С. Шахтные подъемные установки
Подождите немного. Документ загружается.

Продолжительность периода ускоренного движения на
параболическом участке рассматриваемой диаграммы нахо-
дят из уравнения (172). В конце периода ускоренного движе-
ния при t=t
1
``, очевидно, V=V
max
, т.е.
откуда
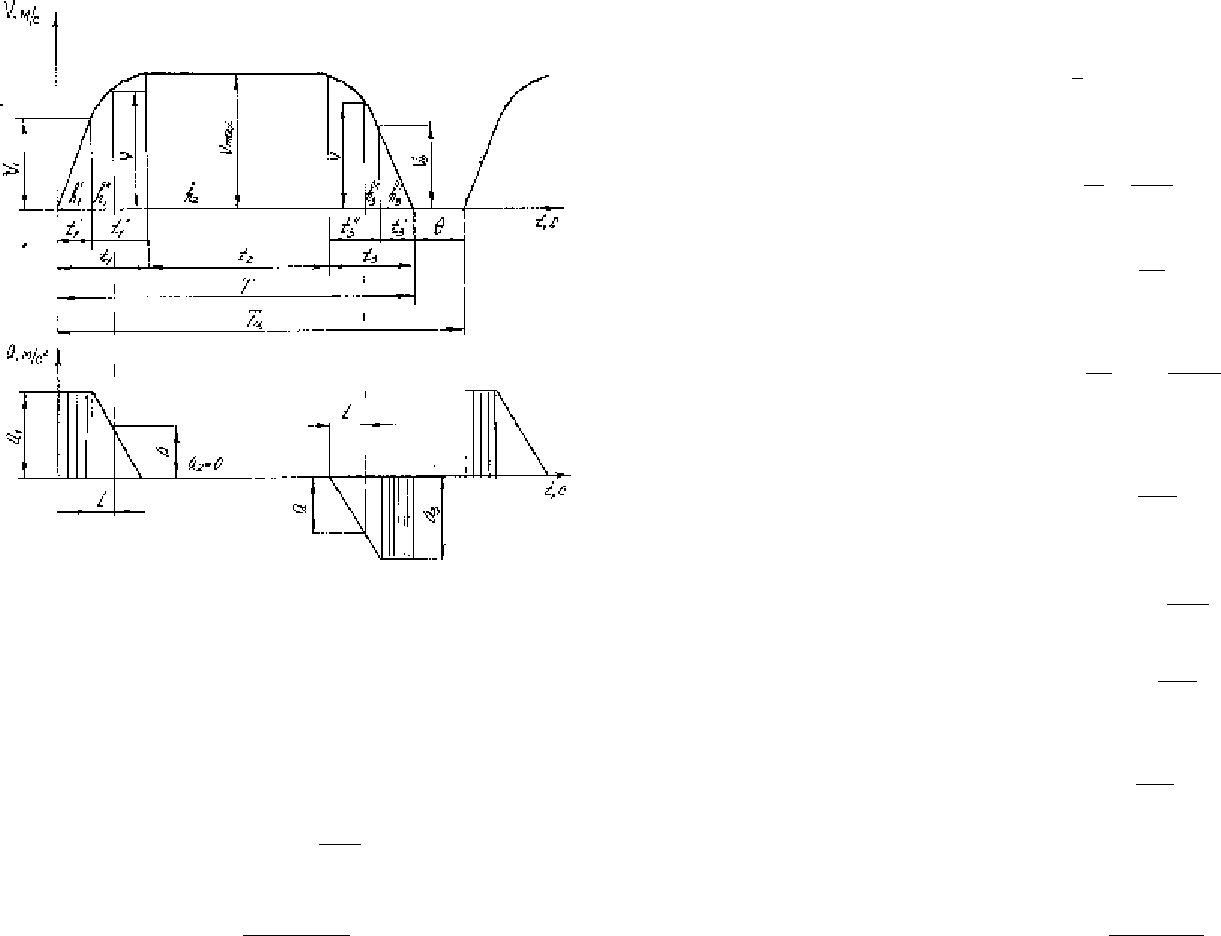
Трехпериодная диаграмма с плавным изменением скорости
в переходные периоды:
a, V и t- текущие значения ускорения, скорости и времени на
параболитическом участке рассматриваемой диаграммы
соответственно в период пуска и замедления.
Рис. 22
Путь h
1
``, пройденный за время t
1
``, определяют из вы-
ражения (174). При t=t
1
``, X=h
1
``
Текущее значение замедления в период времени t
3
`` оп-
ределяют из диаграммы (рис. 22)
откуда
Текущее значение скорости за период времени t
3
``
Постоянная интегрирования С
2
при t= 0 равна макси-
мальной скорости, т.е. С
2
=V
max
, следовательно,
Интегрируя (181), находим путь, проходимый подъем-
ными сосудами за время t
3
``,
или
В начале периода замедления при t=0, X=0, т.е. C
3
=0,
поэтому
Продолжительность периода замедленного движения на
параболическом участке рассматриваемой диаграммы нахо-
дят из уравнения (181). В конце периода замедленного движе-
ния при t=t
3
``, очевидно, V=V
3
t
V V
a
p
1
1
1
2
`` .
.max
=
−
(176)
a
a
t
t
3 3
0
=
−
``
(178)
V V at
at
Vp= = − +.max ``
``
,11
11
1
2
(175)
( )
h at Vt1 1 1 11
1
3
2
`` `` ``.= +
(177)
V adt
at
t
dt
at
t
C= = −
=
−
+
∫∫
3
3
3
3
2
2
2
``
``
.
(180)
a
at
t
=−
3
3``
.
(179)
V V
at
t
p= −.max
``
.
3 2
32
(181)
X Vdt V
at
t
dtp= = −
∫∫
.max
``
,
3
3
2
2
(182)
X V t
at
t
Cp= − +.max
``
.
3
3
3
3
6
(183)
X V t
at
t
p= −.max
``
.
3
3
3
6
(184)
t
V V
a
p
3
3
3
2`` .
.max
=
−
(185)
59
58
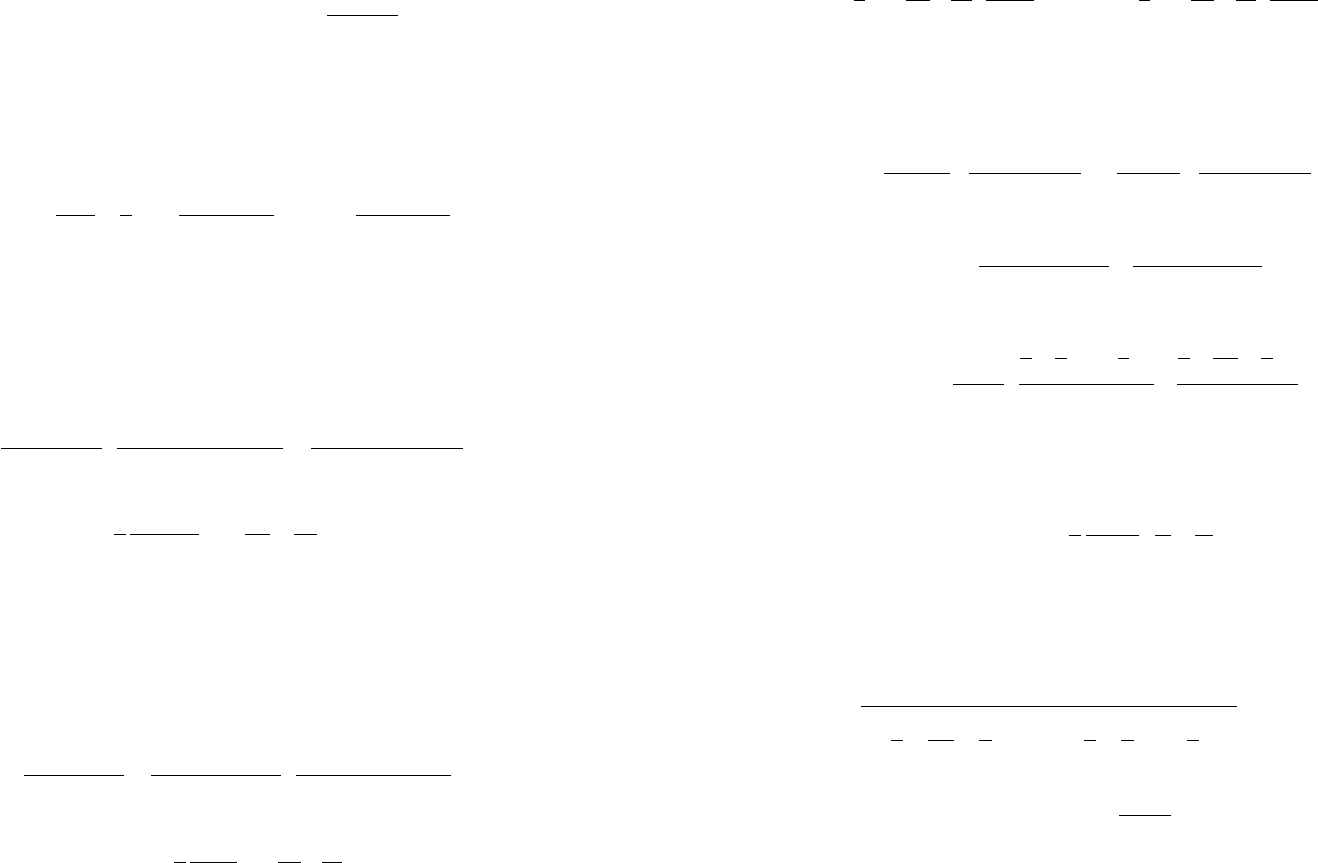
Путь h
3
``, пройденный за время t
3
``, определяют из выра-
жения (184).
При t=t
3
``, X=h
3
``
Путь, проходимый подъемными сосудами в период пус-
ка, при изменении скорости движения от нуля до V
max
Подставляя в (187) вместо h
1
` и h
1
`` их значения, получим
Очевидно, в зависимости от принятой программы изменения
кинематических параметров в период разгона и замедления подъем-
ной установки, скорости V
1
и V
3
могут изменяться от нуля до V
max
.
Подставляя в (188) вместо V
1
=µ
n
V
max
,
где µ
n
- коэффициент, учитывающий характер законо-
мерности изменения скорости движения подъемных сосудов в
период пуска, получим
Решение уравнения (189) имеет вид
Путь, проходимый подъемными сосудами в период за-
медления, при изменении скорости движения от V
max
до нуля.
Подставляя в (191) вместо h
3
` и h
3
`` их значения и учи-
тывая, что V
3
=µ
3
V
max
, где µ
3
- коэффициент, учитывающий ха-
рактер закономерности изменения скорости движения подъем-
ных сосудов в период замедления, получим
Решение уравнения (192) имеет вид
Путь, проходимый сосудами за время подъемного цик-
ла (рис. 22)
где t
2
- продолжительность периода равномерного дви-
жения
или
После упрощения (195) получим
Подставляя в (193) вместо t
2
его значение, имеем
Нетрудно заметить, что при µ=1, т, е. V
1
=V
3
=V
p.max
(197)
трансформируется в (132), а при µ=0 - приобретает вид
В первом случае ( V
1
=V
max
) диаграмма прямолиней-
ная, во втором, ( V
1
= 0) в период разгона и замедления подъем-
ных сосудов, скорость изменяется по параболической законо-
мерности.
Обозначив в (197) модуль ускорения
получим
Решая (199) относительно максимальной скорости, имеем
t T
V
a
V
a
V
a
V
a
p
n p p n p p
2
1 1
3
3
3
3
2 1 2 1
= − −
−
− +
−
µ µ µ µ.max .max .max .max( ) ( )
.
(195)
t T
V
a
V
a
p
p n p
2
1
3
3
2 2
= −
−
−
−
.max .max( ) ( )
.
µ
µ
(196)
a
aa
a a
M
n
n
=
+ −
+ + −
1 3
1 3 3
4
3 3
2
3
4
3
4
3
5
3
3
2
2
µ
µ µ µ
,
h V t
at
p3 3
3 3
2
6
`` ``
(``)
..max= −
(186)
h
h
h
1 1 1
=
+
`
``.
(187)
h
Vt
a
V V
a
V
V V
a
p p
1
11
1
1
1
1
1
12
1
3
2 2
2
= +
−
+
−`
.
.max .max
(188)
h
V
a
p
n
n
1
1
2
4
3
1
2 8
2
= − −
.max
.
µ µ
(190)
h h h3
3
3= +
`
.
(191)
h
V
a
p
3
3
3
34
3
1
8 2
2
2
= − −
.max
.
µ µ
(192а)
H
V
a
V t
V
a
n
n
p
p
p
= − −
+ + − −
4
3
1
2 8
4
3
1
8 2
2
2
3
2
2
1
2
3
3
µ µ µ µ
.max
.max
.max
,
(193)
(
)
(
)
t T t t T t t t tp p2 1 3 1 1 3 3= − − = − + − +` `` ` ``,
(194)
H V T
V
a a
p p
p
= − +
.max
.max
.
4
3 2
1 1
2
1 3
(198)
H V T
V
a a
p p
p
n
n
= −
+ −
+
+ −
.max
.max
.
2
2 3
2
2
4
3
4
3
5
3
4
3 3
2
3
1
3
3
µ µ
µ
µ
(197)
H V T
V
a
p p
p
M
= −.max
.max
.
2
2
(199)
h
V
a
V
a
V
a
p
n
p n
p
n n
1
2
1 1 1
2
2 2
2
2
4
3
1
2
1
= +
−
+
−
.max
.max
.max
( )
( )
.
µ
µ
µ µ
(189)
h
V
a
V
a
V
a
p
p p
3
3
2
3
3
3
3
3
2
2 2 2
2
2
1
2
3
1
= +
−
−
−
.max
.max .max
( ) ( )
.
µ
µ µ
(192)
61
60

Для обеспечения заданной по проекту производитель-
ности шахтной подъемной установки необходимо выполнения
условия V
p.max
≤V
max
.
Установив действительную максимальную скорость,
определяют остальные расчетные величины диаграммы, пред-
ставленной на рис. 22:
время и путь периода движения с ускорением a
1
время и путь периода движения при изменении скорос-
ти от V
1
до V
max
время и путь периода при изменении скорости от V
max
до V
3
время и путь периода движения с замедлением а
3
путь и время периода установившегося движения
время движения подъемных сосудов за время подъемного цикла
t
V
a
1
1
1
` ,=
(201)
h
Vt
1
11
2
`
`
;=
(202)
h at Vt1 1 1 11
1
3
2
`` (``) ``;= +
t
V V
a
3
3
3
2`` ,
max
=
−
(205)
h V t
at
3 3
3 3
2
6
`` ``
(``)
;max= −
(206)
h
Vt
3
33
2
`
`
;=
(208)
t
V
a
3
3
3
` ,=
(207)
h H h h h h2 1 1 3 3
=
−
−
−
−
` `` `` `,
(209)
t
h
V
2
2
=
max
;
(210)
продолжительность цикла и фактический коэффициент
резерва подъема определяют из выражений соответственно
(147) и (148).
Шестипериодная диаграмма, представленная на рис. 23,
применяется при скипах с данной разгрузкой, приводе посто-
янного тока, автоматизированной схеме управления подъемом.
Величину расчетной максимальной скорости движения
подъемных сосудов определяют из выражения
где T
0
и H
0
- соответственно условное время движения и
условный путь шестипериодной криволинейной диаграммы
скорости, приведенной к трехпериодной,
T t t t t t
=
+
+
+
+
1 1 2 3 3` `` `` `;
(211)
Шестипериодная диаграмма с плавным изменением скорости в
переходные периоды
Рис.23
( )
V Ta Ta Hap p pM M M.max .= − −
2
2
(200)
t
V V
a
1
1
1
2`` ,
max
=
−
(203)
(204)
V Ta Ta Hap M M M.max ( ) ,= − −0 0 0
2
2
(212)
63
62
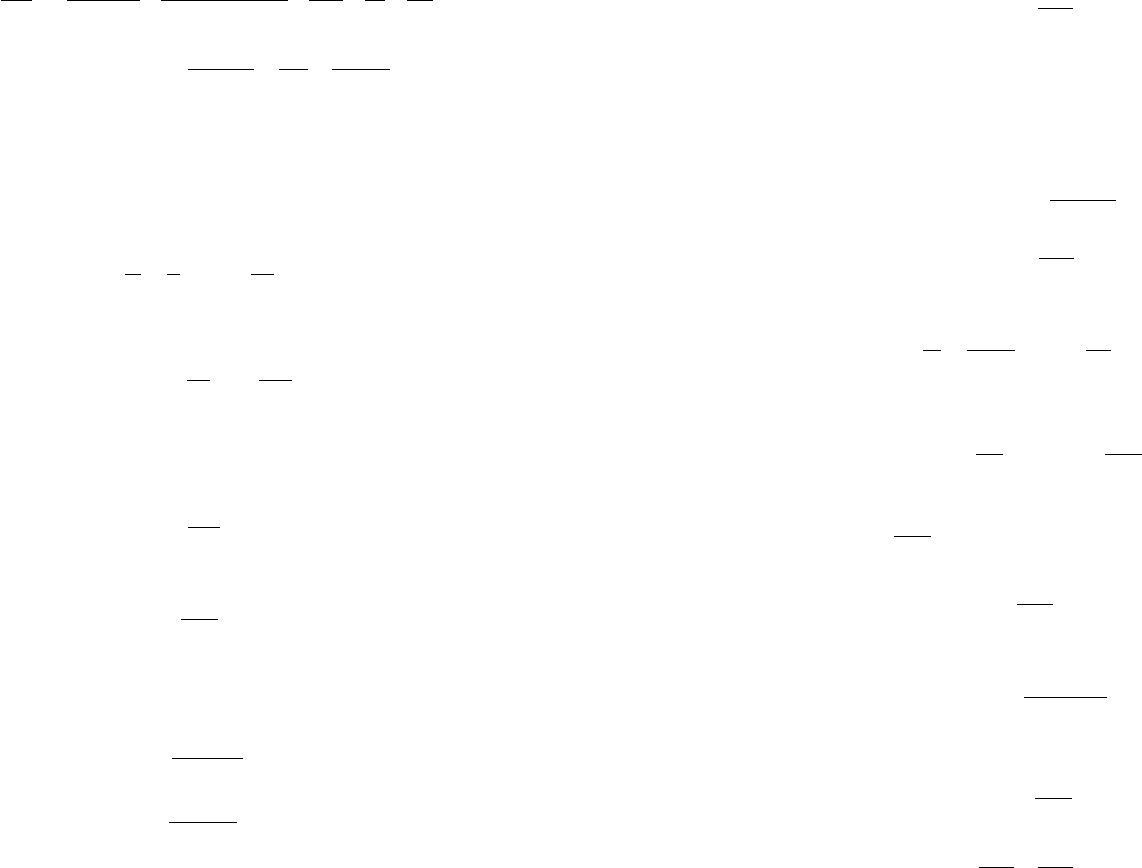
определяют из выражений соответственно (176) и (177).
Время стопорения подъемной машины
Рекомендуемые пределы изменения скорости и ускоре-
ния при стопорении подъемной установки составляют соот-
ветственно V
4
``=0,5 - 1,2 м/с и a
4
``= 0,3 - 0,5 м/с
2
.
Время и путь, проходимый груженым сосудом при дви-
жении его в разгрузочных кривых с постоянной скоростью
дотяжки V
4
``:
Текущее значение ускорения при изменении скорости от
V
4
` до V
4
``
Текущее значение скорости в этот период
при t=0, C=V
4
`,
т.е.
при t=t
4
`
Решая (225) относительно t
4
` , получим
Путь, проходимый сосудами за время изменения скоро-
сти от V
4
` до V
4
``,
или
или
Для удовлетворения проектной производительности
подъемной установки должно выполняться условие:
Текущее значение ускорения в период времени t
0
опре-
деляют из диаграммы (рис.23)
Текущее значение скорости в период движения скипа в
разгрузочных кривых
При t=0 C=0, при t=t
0
, C=V
0
где V
0
- скорость выхода
порожнего скипа из разгрузочных кривых, величину которой
в расчетах принимают равной 1,0-1,5м/с.
Уравнение (217) для условия t=t
0
имеет вид
откуда время движения порожнего сосуда в разгрузоч-
ных кривых
Путь, проходимый подъемными сосудами за этот про-
межуток времени, равен длине разгрузочных кривых h
p
.
Время и путь прямолинейного участка диаграммы скорости:
Время и путь периода изменения скорости от V
1
до V
max
T T t t t t t tp0 0 4 4 4
=
−
−
−
−
+
+
` `` ``` ` ```
(213)
V Vp.max max.
≤
V
at
0
10
2
= ,
t
V
a
0
0
1
2
= .
(218)
h
V V
t1
1 0
1
2
` `.=
+
(220)
t
V
a
4
4
4
```
``
``
.=
h h
V
a
p4
4
4
2
2
``
( ``)
``
,= −
(221)
V
at
t
atV= − +
3
4
3 4
2
2
`
`
t
V V
a
4
4 4
3
2`
` ``
.=
−
(226)
X Vdt
at
t
atV dt= = − +
∫∫
3
4
3 4
2
2`
`
(227)
T T
V
a
V V
a
h V t
V
V
a
V
a
V
a
p
p
0
0
1
4 4
3
4 4
4
4
4
0
1
4
3
2
2
05
= − −
−
−
−
− + +
` `` , `````
``
``
``
`
,
(214)
H H h Vt
at V
a
V
a
p0 4 4
3 4
1
4
3
2
3
2
2
2
0
2 2
= − − + + +``
(`) ( `)
.
(215)
a
a
t
t
a
at
t
1 0 1
0
= → = .
(216)
V adt
at
t
dt
at
t
C= = = +
∫∫
1
0
1
0
2
2
.
(217)
t
V V
a
1
1 0
1
` ,=
−
(219)
t
h
V
p
4
4
=
``
``
.
(222)
(223)
a
a
t
t t
a
at
t
a
3 4
4
3
4
3=
−
→ = −
`
` `
.
V adt
at
t
adt
at
t
at С= = −
= − +
∫∫
3
4
3
3
4
3
2
2` `
(224)
V V
at
at V= = − +4
3 4
3 4 4
2
``
`
` `.
(225)
X
at
t
at
Vt C= − + +
3
4
3
4
3 2
6
2
`
` .
(228)
V
V
V
V
V
V
65
64
При t=0, С=0, при t=t
4
`, X=h
4
`, т.е.
Время и путь периода изменения скорости от V
max
до V
3
определяют из выражений соответственно (185) и (186).
Путь h
2
и время t
2
Продолжительность движения подъемных сосудов за
время цикла
или
Продолжительность подъемного цикла и фактический
коэффициент резерва отпределяют из выражений соответ-
ственно (147) и (148).
Рассмотренная диаграмма скорости наиболее полно
выполняется при автоматизированном управлении подъем-
ной машиной и находит широкое применение на мощных
подъемных установках, оборудованных приводом постоян-
ного тока.
Это скиповые и грузолюдские подъемы,работающие в
режиме по выдаче груза. Система автоматического регулиро-
вания должна обеспечивать программное управление, обеспе-
чивающее выполнение заданной диаграммы скорости, неза-
виаимо от изменения нагрузки в заданных пределах.
У подъемных систем, оборудованных бицилиндрокони-
ческими барабанами, груженая и порожняя ветви за одни и те
же периоды подъемного цикла, за исключением сравнительно
небольшого промежутка времени, когда обе ветви находятся
на большом цилиндре (рис. 24), перемещаясь на разных ра-
диусах органа навивки, имеют разные линейные скорости и
ускорения.
Теоретические исследования закономерностей измене-
ния кинематических параметров подъемных систем, оборудо-
ванных бицилиндроконическими барабанами, следует начи-
нать, очевидно, с диаграмм угловой скорости ω=f(t) и углово-
го ускорения ε=f(t), т.к. изменение последних не связано с из-
менением радиуса навивки.
h Vt
at
4 44
3 4
2
3
` ``
(`)
.= −
(228)
T
t
t
t
t
t
t
=
+
+
+
+
+
0 1 2 3 4 4
```.
(232)
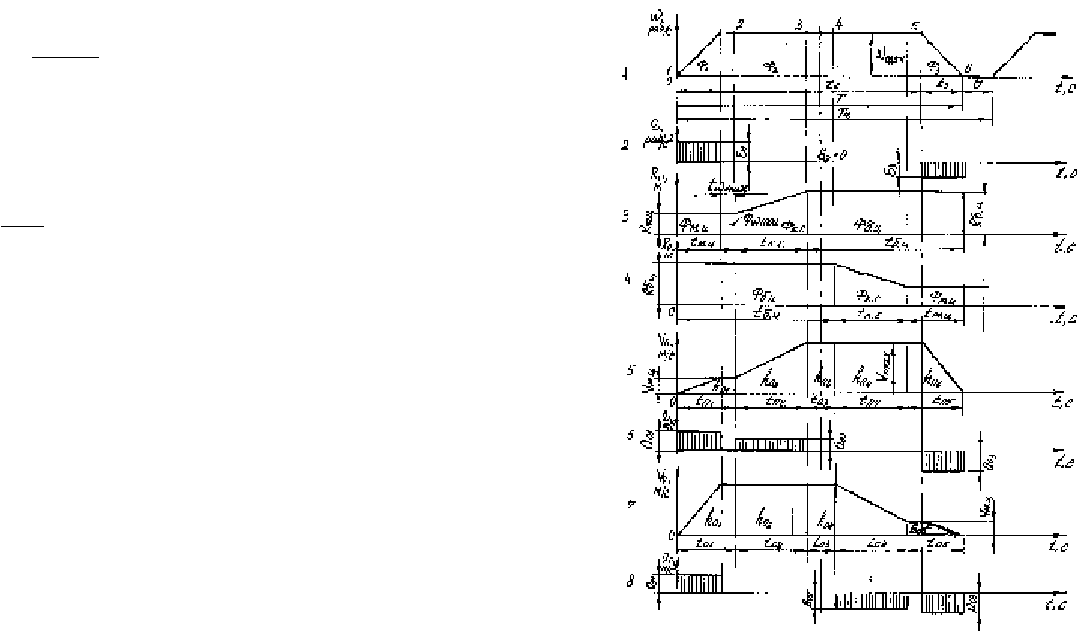
Диаграммы подъемной установки,
оборудованной бицилиндрическим барабаном:
1-угловой скорости; 2-углового ускорения; 3-4-изменения радиуса
органа навивки соотвественно поднимаемой и опускаемой ветвей
каната;5-7-линейные скорости сооствественно поднимаемой и
опускаемой ветви; 6-8-линейного ускорения (замедления)
поднимаемой и опускаемой ветви каната
Рис. 24
Площадь диаграммы угловой скорости (рис.24.1) в маш-
табе представляет собой полный угол поворота органа навив-
ки бицилиндричеокого барабана за время одного подъемного
цикла, т.е
Ф ппол. ,
=
2
π
(233)
h H h h h h h hp2 1 1 3 3 42
=
−
−
−
−
−
−
` `` `` ` `,
(229)
t
h
V
2
2
=
max
.
(230)
T
t
t
t
t
t
t
t
t
t
=
+
+
+
+
+
+
+
+
0 1 1 2 3 3 4 4 4
`
``
``
`
`
``
```
(231)
67
66

где n - сумма всех рабочих витков соответственно на ма-
лом цилиндре, коническом срезе и большом цилиндре.
Или, как видно из рис. 24.1 , полный угол поворота БЦК
барабана за время движения подъемных сосудов Т может быть
представлен
где Ф
1
, Ф
2
и Ф
3
- углы поворота БЦК барабана соответ-
ственно за время разгона t
1
, период равномерного движения с
максимальной угловой скоростью ω
max
-t
2
и
время замедления -
t
3
, град.
Выражение (234) может быть представлено в виде
Решая (235) относительно ω
p.max
, аналогично выводу
формулы (134), получают выражение для определения макси-
мальной расчетной угловой скорости
где модуль углового ускорения, рад/с
2
.
Значения ε
1
и ε
3
определяют в соответствии с требова-
ниями ПТЭ, регламентируемыми для линейных ускорений и
замедлений, т.е.
где ε
1
и ε
3
- угловые ускорение и замедление, рад/с
2
; R
М.Ц.
и R
Б.Ц.
соответственно радиусы малого и большого цилинд-
ров БЦК барабана, м.
Величину действительной линейной максимальной ско-
рости определяют как и для систем с постоянным радиусом
органа навивки (24), (105) и (106). При правильном выборе
величины линейной максимальной скорости должно выпол-
няться условие
Установив действительную максимальную угловую ско-
рость, определяют остальные расчетные элементы трехпери-
одной диаграммы скорости для подъемных систем о перемен-
ным радиусом органа навивки:
время и угол поворота в период ускоренного движения
время и угол поворота в период замедленного движения
угол поворота и время периода равномерного движения
Остальные расчетные величины-диаграммы: Т, Т
ц
и С
ф
определяют как и для систем с постоянным радиусом органа
навивки из выражений (146), (147) и (148).
Диаграммы линейной скорости поднимаемой и опуска-
емой ветвей подъемных канатов (рис. 24.5 и 24.7) строят, учи-
тывая,что текущее значение этой скорости изменяется по за-
кономерности
где ω
x
и R
x
- соответственно текущие значения угловой
скорости и радиуса органа навивки, рад/с и м.
Текущие значения линейных ускорений и замедлений за
время подъемного цикла на диаграммах 6 и 8 (рис. 24) опреде-
ляют из выражений:
в периоды ускоренного и замедленного вращения БЦК
барабана при изменении частоты его вращения соответствен-
но от нуля до ω
max
и от ω
max
до нуля
в периоды вращения органа навивки с максимальной
угловой скоростью, когда поднимающаяся ветвь каната, на-
виваясь на конический срез, движется с ускорением
ε
ε
ε
ε ε
M =
+
1 3
1 3
ε ε1
1
3
3
= =
a
R
a
RМЦ БЦ. . . .
, ,
(237)
t1
1
=
ω
ε
max
,
(239)
Ф
t
1
1
2
=
ω
max
;
(240)
Ф
t
3
3
2
=
ω
max
;
(242)
Ф Ф Ф Фпол2 1 3
=
−
−
. ,
(243)
t
Ф
2
2
=
ω max
.
(244)
a Rx x x
=
ε
;
(246)
t3
3
=
ω
ε
max
,
(241)
Ф Ф Ф Фпол. ,
=
+
+
1 2 3
(234)
Ф t t tпол p p p. .max .max .max .= + +
1
2
1
2
1 2 3ω ω ω
(235)
( )
ω ε ε εp полT T ФM M M.max . ,= − −
2
2
(236)
ωp
БЦ
V
R
.max
max
. .
.≤
(238)
V Rx x x
=
ω
,
(245)
( )
аП
kc
БЦ МЦ
t
R R2= −
ω
max
.
. . . . ,
(247)
69
68

а опускаемая покидает конический срез с замедлением
где t
k.c
- время нахождения ветви подъемного каната на
коническом срезе, с.
Диаграммы линейной скорости, представленные на ри-
сунке 24, содержат пять периодов (t
П1
-t
П5
и t
О1
-t
О5
) при угловой
диаграмме скорости, для которой характерны три известные
периода: t
1
, t
2
и t
3
.
Поэтому возникает необходимость в определении длитель-
ности периодов пятипериодных линейных диаграмм скорости.
Приняв диаграмму угловой скорости симметричной,
определяют :
полный угол поворота малого цилиндра
где n
М.Ц.
- число рабочих витков на малом цилиндре;
угол поворота малого цилиндра, соответствующий перио-
ду движения груженой ветви с максимальной угловой скоростью,
где Ф
1
- угол поворота БЦК барабана при изменении
скорости от нуля до ω
max
, рад;
время, соответствующее этому периоду
время заполнения груженой ветвью каната малого цилиндра
угол поворота конического среза, соответствующий пе-
риоду перехода груженой ветви каната с малого на большой
цилиндр
где n
k.c.
- число рабочих витков на коническом срезе;
время перехода груженой ветви каната с малого на боль-
шой цилиндр
время перехода порожней ветви каната с большого на
малый цилиндр t
k.c.
=t
O4
=t
П4
и время его заполнения ею
t
М.Ц.
=t
О5
=t
П5
определяют аналогично вышеизложенному;
t
Ф
ω
ω
ω
max
max
max
;=
(251)
t t t
Ф
kc П О
kc
. ;..
..
max
= = =2 2
ω
(254)
продолжительность периода, когда и груженая и порож-
няя ветви канатов перемещаются одновременно на радиусе
большого цилиндра с максимальной угловой скоростью
Пути, пройденные подъемными сосудами за соответству-
ющие отрезки времени подъемного цикла, определяют как
площади соответствующих трапеций или прямоугольников,
составляющих пятипериодные диаграммы линейной скорос-
ти на радиусе органа навивки подъемной машины , оборудо-
ванной бицилиндроконичеоким барабаном.
Например:
и т.д.
11. Динамика подъема
В соответствии с основным принципом механики, даю-
щим общий метод решения задач динамики и статики, осно-
ванном на известном принципе Д’Аламбера, материальную
движущуюся систему, к которой приложены все действующие
силы, включая и силы инерции, можно рассматривать как си-
стему, находящуюся в равновесии. Принцип Д’Аламбера
применительно к шахтному подъему: сумма моментов действу-
ющих сил относительно оси вращения уравновешивается сум-
мой моментов сил инерции относительно той же оси, т.е.
где М
дв
- движущий момент, развиваемый приводным
двигателем, Н . м М
ст.
- момент статических сопротивлений,
Н•м; М
дин.
-суммарный момент от действия сил инерции, Н•м.
Для подъемных систем с постоянным радиусом органа
навивки выражение (256) можно представить в виде
где F
дв
.,F
ст.
и F
дин
- усилия подъемной системы соответ-
ственно движущее, статическое и динамическое, взятые отно-
сительно оси вращения органа навивки, Н, R - радиус органа
навивки, м.
Учитывая, что динамический суммарный момент
t
t
T
t
t
П O П П3 3 1 2
2
2
=
=
−
−
.
(255)
h
t t
V h
t t
VП
П
O
O
М Ц1
1
1
1
2 2
=
+
=
+
ω ωmax max
max. .; ;
h
V V
t h t VП
МЦ
П O O2 2 2 2
2
=
+
= ⋅
. . max
max;
M М Мдв ст дин
−
−
=
0,
(256)
FR F R F Rдв ст дин
−
−
=
. . ,0
(257)
( )
аО
kc
МЦ БЦ
t
R R2= −
ω
max
.
. . . . ,
(248)
Ф nМ Ц М Ц. . . . ,
=
2
π
(249)
Ф Ф ФМ Цω max . . ,
=
−
1
(250)
Ф nkc kc. .,
=
2
π
(253)
(252)
t
t
t
t
t
МЦ П О. . max
;
=
=
=
+
1 1 1 ω
71
70
где Σm
i
- приведенная к радиусу органа навивки сум-
марная масса поступательно движущихся и вращающихся ча-
стей подъемной системы, кг; a - текущее значение величины
линейного ускорения (замедления) по диаграмме скорости,
м/с
2
.Выражение (257) можно представить в виде
где знак “плюс” соответствует периоду пуска,“минус” -
замедления.
Статические сопротивления на радиусе органа навив-
ки определяют как разность натяжений поднимаемой и опус-
каемой ветвей подъемного каната, т.е.
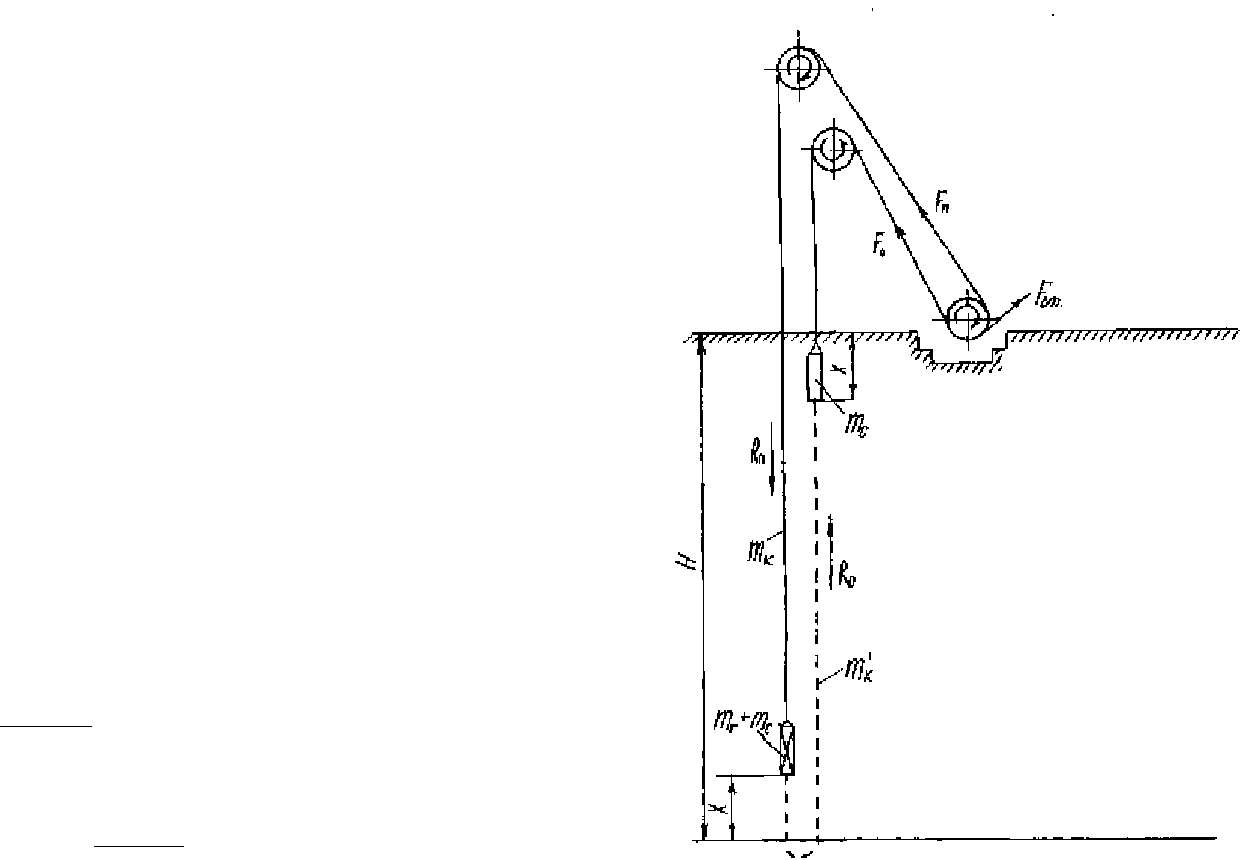
В соответствии с рис. 25 выражение (260) представля-
ют как
где Н - высота подъема, м; Х - текущее значение пути,
проходимого подъемным сосудом за время подъемного цик-
ла, м;R
под.
и R
оп
- вредные сопротивления движению от трения
направляющих о шахтные проводники, изгиба и трения
подъемных канатов на органах навивки и направляющих
шкивах, трения в подшипниках, а также сопротивления воз-
духа движению сосудов соответственно в подымаемой и опус-
каемой ветвях каната, Н.
После упрощения (261) представляют как
Второй сомножитель первого слагаемого в квадратных
скобках называют коэффициентом шахтных сопротивлений, т.е.
Подставляя (263) в (262), получают
F maдин i. ,
=
∑
(258)
F F maдв ст i= ±
∑
,
(259)
K
R R
gm
под оп
Г
=+
+
1
. .
.
(263)
Схема расположения подъемной машины относительно ствола
шахты (к выводу основного уравнения динамики подъема)
Рис. 25
F
F
F
ст под оп. .
.
=
−
(260)
(
)
[
]
( )
[ ]
F gm m mH X mH
R gm mX m H X R
ст Г c k k
под c k k оп
.
. .
`
` ,
= + + − + +
+ − + + − +
(261)
( )( )
F gm
R R
gm
m m H Xст
под оп
k kГ
Г
.
. .
` .= +
+
− − −
1 2
(262)
(
)
(
)
[
]
F gkm m m H Xст k kГ. ` .= − − −2
(264)
73
72

Коэффициент K учитывает сопротивление воздуха при
движении подъемных сосудов, трение в проводниках, в под-
шипниках направляющих шкивов и барабанов, жесткость ка-
натов. Для клетевых подъемов K =1,2, для скиповых K =1.15.
При подъеме в скипах, особенно при использовании оп-
рокидных сосудов, часть их массы передается на разгрузоч-
ные кривые, тем более, что разгрузка начинается раньше, чем
заканчивается подъемный цикл.
С учетом этих обстоятельств в выражение (264) следует
внести корректировку
где β
c
- коэффициент, учитывающий уменвшение массы
полезного груза при движении груженого скипа в разгрузоч-
ных кривых и просыпание части полезного ископаемого в бун-
кер ранее полной остановки подъемного сосуда .
По данным проф. В.И.Киселева β
c
составляет:
опрокидные скипы 0,6-1,0
опрокидные клети 0,6-0,75
скипы с отклоняющимся
кузовом 0,45-0,8
скипы с с секторным
затвором 0,3-0,75,
α
c
- коэффициент учитывающий нарушение уравнове-
шивания собственных масс подъемных сосудов. В выражении
(265) перед вторым слагаемым в квадратных скобках знак
“плюс” соответствует началу, а - “минус” концу подъемного
цикла.
По данным / 9 / α
c
составляет:
опрокидные клети 0,5
опрокидные скипы 0,35
скипы с отклоняющимся
кузовом 0,15
скипы с секторным
затвором,
обыкновенные клети 0.
Текущее значение коэффициентов α
c
и β
c
в периоды
движения подъемных сосудов в разгрузочных кривых, при их
изменении от нуля до максимального значения, принимают
по закону прямой линии:
где X
p
- путь, пройденный подъемным сосудом в раз-
грузочных кривых, за произвольный промежуток времени, м;
h
p
- длина разгрузочных кривых, м.
Основное динамическое уравнение для подъемных сис-
тем с постоянным радиусом органа навивки получают в ре-
зультате совместного решения уравнений (265) и (259)
В состав движущихся частей подъема, имеющего слож-
ную кинематическую схему, входят и поступательно движу-
щиеся элементы (сосуды, масса полезного груза, подъемные
канаты), перемещающиеся с линейным ускорением a= εR, где
ε угловое ускорение, рад/ с
2
; R - радиус органа навивки и эле-
менты ( орган навивки, передачи редуктора, ротор приводно-
го двигателя, копровые шкивы), участвующие во вращатель-
ном движении и имеющие линейные ускорения отличные от
линейного ускорения на радиусе органа навивки.
Вот почему реальные массы поступательно движущих-
ся и вращающихся частей подъемной системы в выражении
(268) заменяют одной суммарной приведенной к радиусу орга-
на навивки массой, величину которой определяют из выраже-
ния (124).
Для окончательного уточненного выбора приводного
двигателя подъема необходимо знать, как он загружен за вре-
мя цикла, т.е его нагрузочную диаграмму, которую строят,
используя выражение (268).
При эксплуатации шахтных подъемных установок воз-
можны следующие режимы работы: m
k
` =0 - подвесной канат
отсутствует, т.е. подъемная система статически неуравнове-
шенная, m
k
`=m
k
- подъемная система статически уравновешен-
ная, m
k
<m
k
` -подъемная система с тяжелым подвесным кана-
том.
Специфический индивидуальный отпечаток на харак-
тер изменения параметров нагрузочной диаграммы, кроме
того накладывают такие характеристики подъемной системы,
как: угол наклона ствола; вид и количество периодов диаг-
раммы скорости, которые зависят соответственно от типа элек-
тропривода и типа подъемного сосуда, конструктивные осо-
бенности органа навивки ( цилиндрические, бицилиндроко-
нические барабаны или ведущие шкивы трения), число подъем-
β βcx c
p
p
X
h
=
(266)
α αcx c
p
p
X
h
= −
1 ,
(267)
(
)
(
)
(
)
[
]
F k m m m m H Xст с Г с c k k. ` ,= − ± − − −β α 2
(265)
(
)
(
)
(
)
[
]
F gk m m m m H X mac c c k k iГ= − ± − − − ±
∑
β α ` .2
(268)
75
74

ных канатов, наличие подъемного сосуда как в подымаемой,
так и в отпускаемой ветвях каната (двухконцевые, однокон-
цевые, односкиповые или одноклетевые с противовесом
подъемные системы).
На рис. 26 представлены диаграммы подъемной уста-
новки, оборудованной неопрокидными клетями. Отметив на
диаграмме скорости характерные точки 1-6, определяют в них
величины движущих усилий,используя выражение (268).
Подъемная система статически неуравновешена, т.е.
m
k
`=0. В соответствии с (268) для рассматриваемой системы
основное уравнение динамики имеет вид
Движущие усилия в характерных точках диаграммы ско-
рости:
в начале подъемного цикла
в конце периода ускоренного движения
в начале периода равномерного движения
в конце периода равномерного движения
в начале замедленного движения
в конце подъемного цикла
Для статически уравновешенной подъемной системы, где
m
k
=m
k
`, основное динамическое уравнение имеет вид
В рассматриваемом случае движущие усилия в харак-
терных точках диаграммы скорости определяют, используя вы-
ражение (270): в начале и конце периода равномерно ускорен-
ного движения
[
]
F gkm mH maГ k i1 1= + +
∑
;
(
)
[
]
F km mH h maГ k i2 1 12= + − +
∑
;
(
)
[
]
F gkm mH hГ k3 12= + − ;
(
)
[
]
{
}
F gkm mH h hГ k4 1 22= + − + ;
(
)
[
]
{
}
F gkm mH hh maГ k i5 1 2 32= + − + −
∑
;
(
)
F gkm mH maГ k i6 3= − −
∑
.
F F gkm maГ i1 2 1= = +
∑
;
Диаграммы подъемной установки,
оборудованной обыкновенными клетями:
а-скорости; б-ускорения; в-движущих усилий; г-мощности на валу
подъемной машины, затрачиваемой исключительно на подъем
полезного груза
Рис. 26
(
)
[
]
F gkm mH X maст k iГ. .= + − ±
∑
2
(269)
F gkm maГ i
=
±
, (270)
77
76
