Шивринский В.Н. (под редак.) Проектирование приборов, систем и измерительно-вычислительных комплексов
Подождите немного. Документ загружается.


31
Рассмотрим задачу измерения температуры в диапазоне от 0 до 150
o
C, для
которой имеется семь видов чувствительных элементов: дилатометрический,
биметаллический, жидкостный, газовый, парожидкостный, терморезисторный,
термоэлектрический. Любой из перечисленных элементов может работать в за-
данном диапазоне температур, однако предпочтение следует отдать последним
двум, основанным на чисто электрических принципах. Остается выбрать один
из двух элементов и здесь преимущество на стороне терморезистора, поскольку
термоэлектрические чувствительные элементы в рассматриваемом диапазоне
температур развивают слишком малую термоэлектродвижущую силу.
Другой пример – измерение абсолютного давления в диапазоне от 800 до
6 мм рт. ст. Здесь также существует несколько видов чувствительных элемен-
тов: пьезорезисторный, тепловой, электронный, газоразрядный, радиоактивный,
упругий (мембрана, сильфон, трубчатая пружина). Пьезорезисторный элемент
работает в области очень высоких давлений, следующие три элемента – в об-
ласти очень низких давлений.
Остаются для выбора два чувствительных элемента, способные работать
в заданном диапазоне: радиоактивный элемент – электрический и упругий эле-
мент – механический. Радиоактивный элемент имеет слишком слабый сигнал –
выходной ток равен 10
-9
-10
-16
А и его трудно измерить с высокой точностью.
В данном случае наиболее приемлем механический (упругий) элемент, выход-
ным сигналом которого может служить одна из двух величин – упругая дефор-
мация или сила.
При решении некоторых задач можно встретиться со случаями, когда от-
сутствуют чувствительные элементы, позволяющие осуществить нужное пре-
образование, или когда применение существующих элементов приводит к
слишком грубым или громоздким решениям. В этих случаях можно прибегнуть
к методу косвенных измерений, при котором чувствительный элемент воспри-
нимает не измеряемую величину Х, а некоторую другую величину Х
1
, связан-
ную с Х известной функциональной зависимостью
Х
1
= f
1
(Х). (4.1)
Уравнение (4.1) является уравнением метода измерения. Чувствительный
элемент преобразует величину Х
1
в некоторый сигнал У
1
У
1
= f
2
(Х
1
). (4.2)
Уравнение (4.2) является характеристикой чувствительного элемента. По
уравнениям (4.1) и (4.2) нетрудно найти зависимость У
1
от Х
У
1
= f
2
[f
1
(X)] = f(X).
Примером прибора, основанного на методе косвенных измерений, служит
барометрический высотомер, в котором в качестве уравнения метода измерения
используется известная функциональная зависимость атмосферного давления P
от высоты полета H. В интервале высот от 0 до 11 км зависимость H от P выра-
жается формулой
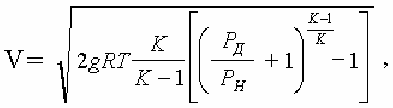
32
здесь H – высота полета, м; P
H
– абсолютное давление на высоте полета, н/м
2
;
P
0
– абсолютное давление у поверхности Земли; τ – температурный градиент
(τ = 0,0065 град/м); R – газовая постоянная (R = 29,27 м/град); T
0
– абсолютная
температура у поверхности Земли (T = 273 + t
o
C).
При градуировке прибора параметры P
0
, T
0
, τ и R считают постоянными.
Встречаются случаи, когда метод косвенных измерений дает зависимость
измеряемой величины Х не от одной, а от нескольких независимых переменных
Х
1
, ..., Х
k
, каждая из которых может быть измерена своим чувствительным эле-
ментом. Например, для указателя истинной воздушной скорости уравнение ме-
тода измерения имеет вид
здесь g – ускорение силы тяжести (g = 9,81 м/с
2
); T – абсолютная температура
на высоте полета; k – отношение теплоемкостей воздуха при постоянном дав-
лении и постоянном объеме (k = 1,4); P
д
– динамическое давление; V – истинная
воздушная скорость.
Измеряя T, P
д
и P
H
с помощью трех чувствительных элементов, можно оп-
ределить V, считая параметры g, R, k постоянными.
Существуют измерительные информационные системы, в которых изме-
ряемые величины являются функциями еще большего количества независимых
переменных, каждая из которых измеряется своим чувствительным элементом.
Например, бесплатформенная инерциальная навигационная система содер-
жит шесть чувствительных элементов (три акселерометра и три гироскопа).
Получая информацию от этих чувствительных элементов, цифровой вычисли-
тель решает известные уравнения и определяет широту и долготу местополо-
жения летательного аппарата, а также ряд других навигационных параметров.
Выбор метода измерения и формирование структурной схемы
Если прибор служит в качестве измерительного устройства с визуальным
отсчетом, то его выходным сигналом должно быть угловое (линейное) переме-
щение стрелочного указателя или показания цифрового отсчетного устройства.
В простейшем случае выходной сигнал чувствительного элемента служит вы-
ходным сигналом прибора. Примером является биметаллический термометр.
При изменении температуры биметаллическая спираль вместе со стрелкой за-
кручивается на достаточно большой угол, поддающийся непосредственному
отсчету по шкале прибора.
Однако в большинстве измерительных приборов приходится применять до-
полнительные преобразователи для превращения выходного сигнала чувстви-
тельного элемента в достаточно большое перемещение стрелочного указателя
или цифровой код управления электронным индикатором.
Если прибор выполняет функции датчика в системе автоматического
управления или контроля, то в простейшем случае сам чувствительный элемент
и является таким датчиком (термосопротивление, термопара).
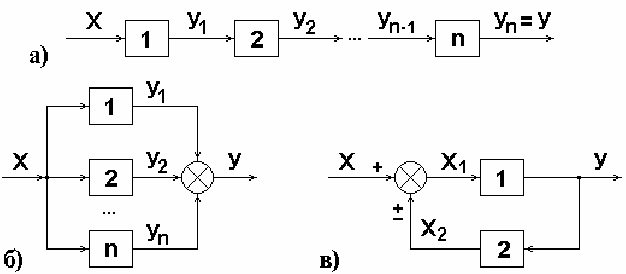
33
Сложные датчики, кроме чувствительного элемента, содержат и другие
преобразователи, изменяющие род физической величины (например, механиче-
ское перемещение в электрический сигнал) и масштаб выходного сигнала, или
функциональную зависимость между входным и выходным сигналами.
Наиболее распространены два метода преобразования выходного сигнала
чувствительного элемента У
1
в выходной сигнал датчика У нужной формы и
масштаба: метод последовательного преобразования и компенсационный ме-
тод. В методе последовательного преобразования сигнал У
1
преобразуется в
другой сигнал У
2
, затем сигнал У
2
преобразуется в У
3
и т. д.; в конечном счете,
получается выходной сигнал У. Вид и количество преобразований зависят от
типа чувствительного элемента и от требований к форме и масштабу выходного
сигнала У.
В компенсационном методе сигнал У
1
уравновешивается другим сигналом
У
0
, создаваемым с помощью так называемого обратного преобразователя. Ком-
пенсационный метод может сочетаться с методом последовательного преобра-
зования, например, сигнал У
1
преобразуется в У
2
, а затем сигнал У
2
уравнове-
шивается сигналом У
0
обратного преобразователя.
Различие между указанными методами можно проиллюстрировать с помо-
щью структурной схемы. Структурная схема прибора является отображением
его принципиальной схемы и дает представление о видах и порядке физических
преобразований, осуществляемых данным прибором в процессе измерения.
Каждый вид преобразования условно изображается на структурной схеме
отдельным звеном, являющимся элементарным преобразователем физических
величин. При использовании метода косвенных измерений преобразование, от-
вечающее данному методу, отображается на структурной схеме в виде специ-
ального звена.
Чтобы определить статическую характеристику прибора, необходимо опре-
делить статические характеристики всех его звеньев. Расчет характеристик
звеньев ведется на основе анализа физических принципов их работы.
Звенья могут соединяться между собой одним из трех типовых способов:
последовательно (рис. 4.1, а) параллельно (рис. 4.1, б) и встречно-параллельно
(рис. 4.1, в).
Рис. 4.1. Типовые соединения звеньев: а) последовательное;
б) параллельное; в) встречно-параллельное; 1, 2,...n – звенья
34
Для встречно-параллельного соединения (рис. 4.1, в) звено 2, расположен-
ное во встречной цепи, называют обратным преобразователем. Выходной сиг-
нал X
2
обратного преобразователя может суммироваться с входным сигналом Х
с тем же знаком (положительная обратная связь) или с обратным знаком (отри-
цательная обратная связь).
Схемы, в которых звенья соединены последовательно или параллельно, яв-
ляются разомкнутыми; схема со встречно-параллельным соединением является
замкнутой. Структурная схема прибора может содержать различные виды со-
единений звеньев и быть замкнутой не полностью, а на отдельных участках.
Рассмотрим особенности структурных схем, отображающих описанные
выше методы преобразования сигналов. Методу последовательного преобразо-
вания отвечает разомкнутая структурная схема (рис. 4.1, а), где звено 1 с вы-
ходным сигналом У
1
является чувствительным элементом, а остальные звенья
2, 3, ..., n – дополнительные преобразующие элементы.
Примером прибора с последовательным преобразованием сигналов служит
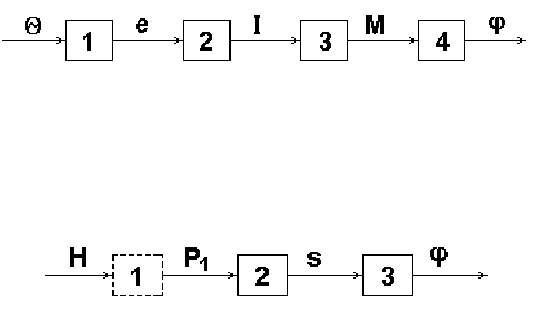
термоэлектрический термометр. Структурная схема прибора (рис. 4.2) содер-
жит четыре последовательно соединенных звена: 1 – термопара (преобразует
температуру Θ в термоЭДС е); 2 – электрическая цепь (преобразует термоЭДС
е в силу тока I); 3 – магнитоэлектрический измерительный механизм (преобра-
зует силу тока I во вращающий момент М); 4 – упругая подвижная система
(преобразует момент М в угловое перемещение ϕ, являющееся выходным сиг-
налом прибора).
Рис. 4.2. Структурная схема термоэлектрического термометра
Другим примером измерительного прибора, построенного по методу по-
следовательного преобразования сигналов, является барометрический высото-
мер (рис. 4.3).
Рис. 4.3. Структурная схема барометрического высотомера
В структурной схеме высотомера перед чувствительным элементом 2
включено условное звено 1, отображающее преобразование высоты H в давле-
ние P
1
в соответствии с уравнениями, лежащими в основе метода косвенного
измерения высоты. Чувствительным элементом 2 служит анероидная коробка,
преобразующая давление P
1
в линейное перемещение s, которое затем преобра-
зуется в угловое перемещение ϕ с помощью шатунно-кривошипной передачи
(звено 3), связанной с указателем. Угол ϕ служит выходным сигналом прибора.
Структурная схема прибора, построенного по компенсационному методу,
приведена на рис. 4.4, которая является замкнутой на участке между выходом
чувствительного элемента У
1
и выходом прибора У.

35
Замыкание схемы осуществляется на входе звена 2 с помощью отрицатель-
ной обратной связи (выходной сигнал У
0
обратного преобразователя подается
на вход звена 2 с обратным знаком).
Рис. 4.4. Структурная схема прибора, построенного
по компенсационному методу
На схеме рис. 4.4 звено 1 отображает чувствительный элемент, звено 2 –
нуль-орган, звено 3 – интегрирующий элемент, звено 4 – обратный преобразо-
ватель. Нуль-орган 2 вырабатывает сигнал У
2
, пропорциональный разности
(У
1
– У
0
) с соответствующим знаком, а интегрирующий элемент 3 осуществляет
интегрирование У
2
и наращивает выходной сигнал У, а вместе с ним (через об-
ратный преобразователь) и сигнал обратной связи У
0
до тех пор, пока разность
(У
1
– У
0
) не станет равной нулю; при этом система приходит в состояние рав-
новесия. Если известна статическая характеристика обратного преобразователя
У
0
= f
0
(У), то для положения равновесия (когда У
0
= У
1
) можно записать
У
1
= f
0
(У) или У = Ψ
0
(У
1
),
где Ψ
0
– функция, обратная f
0
.
Зная характеристику чувствительного элемента У
1
= f
1
(X), нетрудно найти
характеристику всего прибора:
У = Ψ
0
[f
1
(X)].
Примером прибора, построенного по компенсационному методу измерения,
является электроемкостный топливомер (рис. 4.5).
Рис. 4.5. Структурная схема электроемкостного топливомера
Чувствительным элементом служит погруженный в бак с топливом конден-
сатор (звено 1), емкость которого C
x
зависит от высоты h уровня топлива. Нуль-
органом (звено 2) служит мостовая электроизмерительная схема. Выходное на-
пряжение U
1
мостовой схемы усиливается усилителем переменного тока (зве-
но 3). Роль интегрирующего элемента (звено 4) выполняет электродвигатель, на
вход которого подается напряжение U
2
. Обратным преобразователем является
потенциометр (звено 5), движок которого связан через редуктор с электродви-
гателем. Емкость чувствительного элемента C
x
и сопротивление R
x
потенцио-
метра образуют два переменных плеча мостовой схемы (два других плеча R
0
и
C
0
– постоянные величины).
36
Данная схема имеет некоторое отличие от рассмотренной выше: нулевой
сигнал на выходе нуль-органа имеет место не при равенстве сигналов чувстви-
тельного элемента и обратного преобразователя, а при соблюдении условия
равновесия мостовой схемы. Выходным сигналом прибора служит угол ϕ пово-
рота выходной оси редуктора и связанной с ним стрелки указателя.
В результате сравнения метода последовательного преобразования сигна-
лов с компенсационным методом можно сделать вывод, что схема метода по-
следовательного преобразования проще. Однако с помощью компенсационного
метода может быть получена более высокая точность, так как в условие равно-
весия системы практически не входят параметры всех остальных преобразую-
щих элементов, кроме чувствительного элемента и обратного преобразователя.
Поэтому в тех случаях, когда не требуется очень высокая точность измере-
ния, используют метод последовательного преобразования и строят прибор по
разомкнутой структуре. В точных приборах применяют компенсационный ме-
тод и структурную схему делают замкнутой.
Практически приборы с погрешностями, превышающими 1% от диапазона
измерения, строят по методу последовательного преобразования сигналов; при-
боры с погрешностями менее 0,1% строят по компенсационному методу; в при-
борах с погрешностями от 0,1 до 1% используют как тот, так и другой методы.
Принципы конструирования приборов
При конструировании приборов широко используются нормализованные
детали (винты, гайки, шайбы и др.), радиоэлектронные элементы (резисторы,
конденсаторы, диоды, транзисторы, интегральные микросхемы и др.), узлы и
готовые изделия (шарикоподшипники, электродвигатели, зубчатые редукторы,
штепсельные разъемы и др.).
Выбор нормализованных изделий производится из действующих нормалей,
каталогов, стандартов. Применение нормализованных деталей и узлов сокра-
щает время разработки, удешевляет прибор и повышает его надежность, по-
скольку освоенные в крупносерийном производстве нормализованные детали и
узлы имеют более высокое качество, чем специальные, выпускаемые малыми
партиями.
Эффективным средством повышения качества приборов и их удешевления
является широкая унификация их конструкций. Унифицированные приборы,
благодаря их крупносерийному и массовому выпуску, лучше отработаны, в ре-
зультате чего они более надежны и дешевы, чем приборы узкого применения.
Унификация конструкций приборов осуществляется в следующем порядке.
В начале производится сбор исходных данных у возможных потребителей при-
боров с целью выяснения необходимых диапазонов измерения, характеристик,
точности, срока службы и условий эксплуатации. После этого разрабатывается
и согласовывается со всеми потребителями ТЗ на проектирование унифициро-
ванного прибора. В ТЗ определяется минимальное число типоразмеров или мо-
дификаций прибора, отличающихся диапазонами измерения и классами точно-
сти и обеспечивающих выполнение требований всех потребителей.
37
В процессе конструирования прибора нужно стремиться к тому, чтобы все
модификации имели по возможности единую конструкцию, а переход от одно-
го диапазона измерения к другому (или от одного класса точности к другому)
сопровождался минимальными изменениями, например, заменой какого-то од-
ного узла или нескольких деталей.
Эффект от унификации тем больше, чем на более высоком уровне она про-
водится. Унификация информационно-измерительной системы приводит к зна-
чительно большему выигрышу в качестве изделия и его стоимости, чем унифи-
кация отдельного прибора или датчика.
Чем выше уровень унификации, тем труднее выполнить технические тре-
бования. Например, к навигационным системам, предназначенным для приме-
нения на легких самолетах, предъявляются очень жесткие требования в части
габаритно-весовых характеристик, но в то же время требования к точности ме-
нее жесткие по сравнению с системами, предназначенными для тяжелых само-
летов. Если ставится задача создания унифицированной навигационной систе-
мы, которая может быть применима на всех самолетах (легких и тяжелых), то
такая система должна иметь минимальные габариты и массу, отвечающие тре-
бованиям для легких самолетов, и в то же время обладать наивысшей точно-
стью, удовлетворяющей требованиям для тяжелых самолетов.
Снижение габаритных размеров и массы унифицированных систем расши-
ряет область их применения. Большое значение для создания унифицированных
приборов имеет применение микроэлектроники с высокой степенью интегра-
ции. При этом уменьшаются размеры и масса прибора, повышается надеж-
ность, снижается стоимость. Наибольший выигрыш в объеме конструкции дают
большие интегральные схемы.
Глава 5. Расчет характеристик приборов и систем
Общие понятия
Приборы и системы могут работать в статическом и динамическом режи-
мах. В статическом режиме измеряемая величина постоянна и выходной сигнал
прибора приобретает установившееся значение. В динамическом режиме изме-
ряемая величина и выходной сигнал прибора изменяются с течением времени.
Соответственно расчет характеристик приборов и систем делится на расчет ста-
тических и динамических характеристик. Различают заданную и расчетную
статические характеристики. Заданная характеристика – это зависимость между
У и Х, требуемая по техническому заданию
У
зад
= f
зад
(X). (5.1)
Расчетная характеристика получается в результате расчета конкретной схе-
мы и конструкции прибора
У = f(X, q
1
, ..., q
n
), (5.2)
где q
1
, ..., q
n
– параметры схемы и конструкции, в число которых входят как
геометрические параметры (размеры деталей), так и физические параметры
(модуль упругости, электропроводность, магнитная проницаемость и т. п.).
38
Параметры q
1
, ..., q
n
в различных образцах однотипных приборов отличают-
ся от номинальных значений вследствие влияния технологических факторов в
процессе изготовления приборов, а также могут изменяться в процессе экс-
плуатации из-за изменения режимов питания и окружающих условий (темпера-
туры, атмосферного давления и др.). Поэтому в уравнении (5.2) величина У яв-
ляется функцией многих переменных, что учитывается при анализе погрешно-
стей. Если в уравнении (5.2) все параметры приравнять их номинальным рас-
четным значениям и считать постоянными (q
1
=q
10
, q
2
=q
20
, ..., q
n
=q
n0
), то это
уравнение будет выражать номинальную расчетную характеристику
У
ном
= f(X, q
10
, ..., q
n0
). (5.3)
Если при этом учесть, что q
10
, ..., q
n0
– постоянные, то номинальную расчет-
ную характеристику можно записать как функцию одного переменного
У
ном
= f(X). (5.4)
Методы расчета статических характеристик
Расчет статических характеристик приборов и систем ведется в следующем
порядке:
– составляется структурная схема прибора (системы);
– рассчитывают характеристики и чувствительность всех звеньев исходя из
принципов их работы, схемы и конструкции;
– производят расчет характеристики и чувствительности прибора (системы)
в целом, исходя из вида структурной схемы.
Характеристики звеньев определяются путем анализа физических законов,
лежащих в основе их работы. Методы расчета типовых элементов изложены
в специальной литературе (например, по курсам «Элементы приборных уст-
ройств», «Электроника», «Электротехника» и др.).
Иногда характеристики элементов не поддаются точному расчету, но могут
быть определены экспериментально. В подобных случаях для получения анали-
тической зависимости можно применить аппроксимирующую функцию. На-
пример, характеристику термоэлектрического элемента, преобразующего тем-
пературу Θ в электродвижущую силу
e
, определяют по экспериментально по-
лученным справочным данным, в которых даны в виде таблиц значения
e
при
различных значениях Θ.
Задаваясь аналитической зависимостью в виде полинома 2-й степени
(
e
=α
1
Θ+α
2
Θ
2
), можно так подобрать коэффициенты α
1
и α
2
, чтобы вычислен-
ные по этой формуле значения
e
приближались к табличным данным. Для бо-
лее точного приближения можно выбрать в качестве аппроксимирующей функ-
ции полином 3-й степени.
После того как получены уравнения всех звеньев, входящих в структурную
схему, определяется характеристика прибора в целом. С этой целью совместно
решаются уравнения звеньев и уравнения дополнительных связей между звень-
ями, отображающие операции суммирования или вычитания сигналов на струк-
турной схеме.

39
Для типовых соединений звеньев (рис. 4.1) можно вывести стандартные
формулы, выражающие статическую характеристику и чувствительность при-
бора через характеристики и чувствительность звеньев.
Последовательное соединение (рис. 4.1, а). Если характеристики звеньев
1, 2, ..., n выражены соответственно уравнениями
У
1
= f
1
(X);
У
2
= f
2
(У
1
);
. . . . . . . . . .
У
n-1
= f
n-1
(У
n-2
);
У = f
n
(У
n-1
),
(5.5)
то результирующая характеристика прибора определяется совместным решени-
ем системы уравнений (5.5):
У = f
n
{f
n-1
...f
2
[f
1
(X)]} (5.6)
Чувствительность прибора
S = ∂У/∂X.
Умножим и разделим правую часть данного равенства на ∂У
1,
∂У
2
,
...,
∂У
n-1
,
тогда чувствительность прибора определится как
S = (∂У
1
/∂X)(∂У
2
/∂У
1
)..(∂У/∂У
n-1
).
Имея в виду, что
∂У
1
/∂X = S
1
; ∂У
2
/∂У
1
= S
2
; ... ∂У/∂У
n-1
= S
n
,
получим окончательно
Характеристику прибора можно определить и графическим путем. Для
прибора с тремя последовательно соединенными звеньями в четвертях I, II, III
прямоугольной системы координат строят соответственно характеристики
звеньев 1, 2, 3, а затем с помощью построения определяют результирующую
характеристику прибора в IV четверти.
Если прибор содержит более трех звеньев, то построение ведется в не-
сколько этапов. В начале находят характеристику соединения из первых трех
звеньев, затем повторяют построение на другом графике, рассматривая первые
три звена как одно звено.
В качестве примера рассмотрим расчет статической характеристики маят-
никового акселерометра, схема которого приведена на рис. 5.1, где m, l – масса
и длина маятника; C
пр
– жесткость противодействующей пружины; U
o
, ϕ
o
– на-
пряжение питания и полный рабочий угол потенциометра;
a
– измеряемое ус-
корение; U
вых
, ϕ – выходное напряжение и угол поворота движка потенциомет-
ра; F – сила, действующая на массу; M
вр
– вращающий момент; M
пр
– противо-
действующий момент.
Акселерометр работает при малых отклонениях, тогда F ≈ ma.
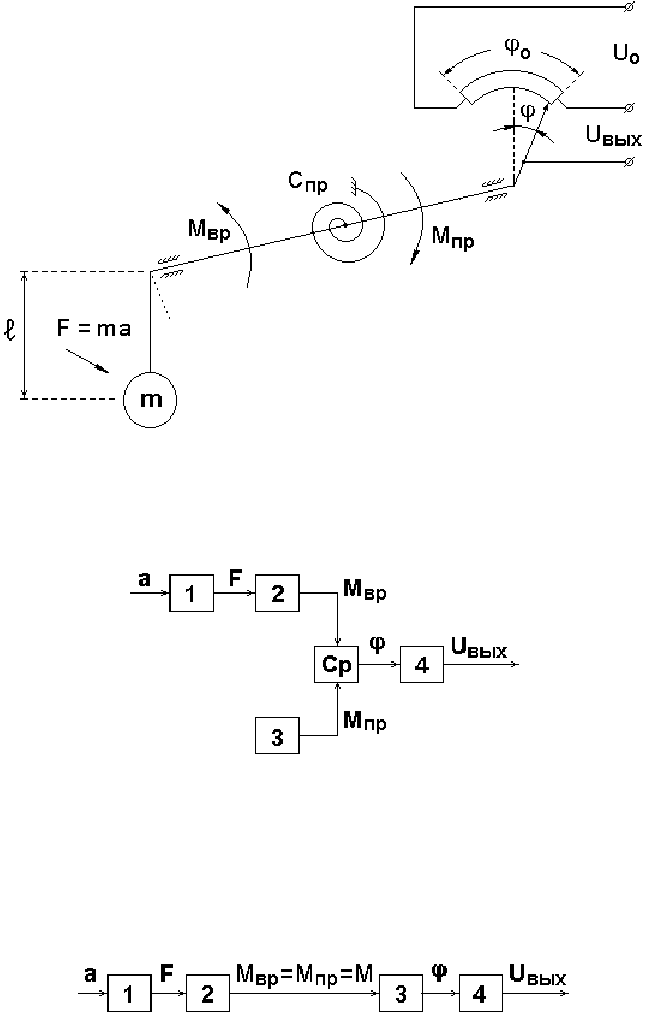
40
Рис. 5.1. Схема маятникового акселерометра
Структурная метрологическая схема маятникового акселерометра приведе-
на на рис. 5.2.
Рис. 5.2. Структурная метрологическая схема
маятникового акселерометра
Структурная (динамическая) схема маятникового акселерометра приведена
на рис. 5.3. Операция сравнения здесь как бы пропадает, хотя и показано, что
M
вр
= M
пр
.
Рис. 5.3. Структурная схема маятникового акселерометра
Характеристики звеньев 1, 2, 3, 4 выражены соответственно уравнениями
F = ma;
M
вр
= Fl;
M
пр
= C
пр
ϕ;
U
вых
= U
o
ϕ/ϕ
o
. (5.8)
Жесткость спиральной пружины определяется как
C
пр
= bh
3
E/12L, (5.9)
где L – развернутая длина, b – ширина, h – толщина, E – модуль упругости ма-
териала спиральной пружины.
