Ширапов Д.Ш. Основы вычислительной математики. Выпуск 6. Методы решения дифференциальных уравнений с частными производными
Подождите немного. Документ загружается.

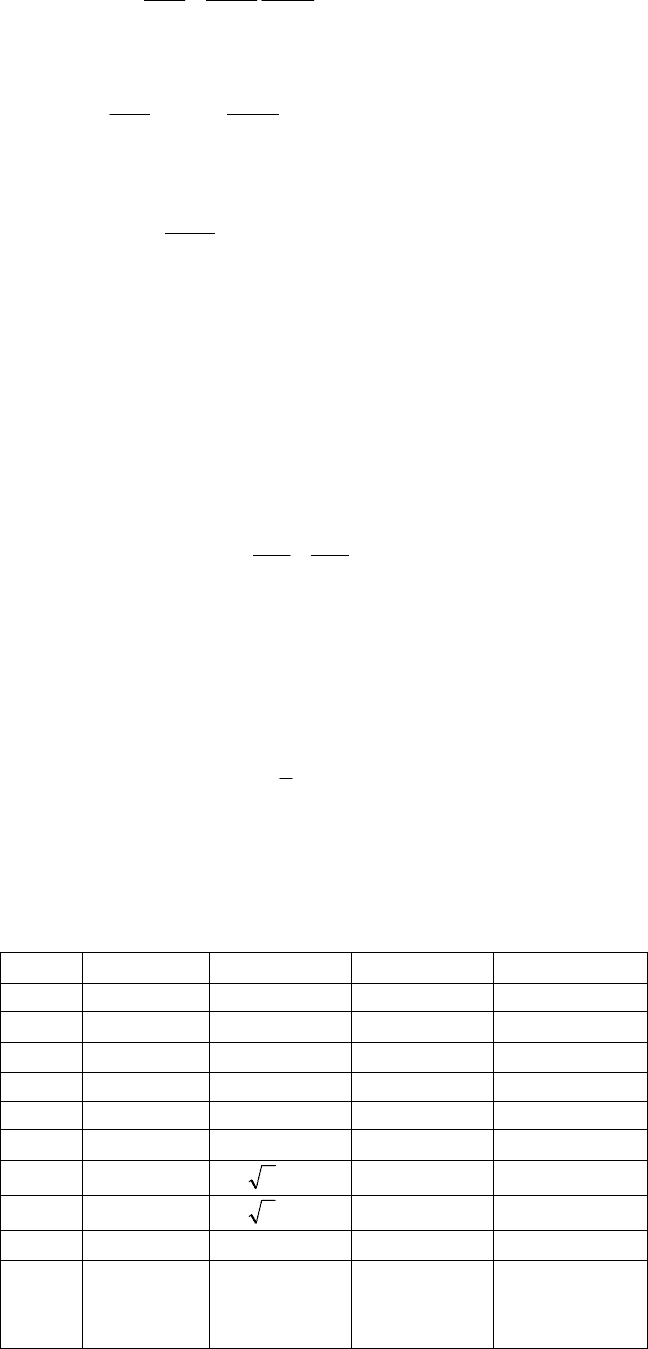
2
2
22
1
2
x
u
ka
t
u
kuu
ioio
ioi
∂
∂
+
∂
∂
+≈
. (9.8)
Из начальных условий (9.2), предполагая, что f(х)
∈
С
(2)
[0,l], получаем:
u
io
=f
i ,
i
io
F
t
u
=
∂
∂
,
"
2
2
i
io
f
x
u
=
∂
∂
. (9.9)
Подставляя эти значения в формулу (9.8), окончательно находим
"
22
1
2
iiii
f
ka
kFfu ++≈ . (9.10)
Очевидно, формулу (9.10) целесообразно применять в том случае, когда функция f(х) задана
аналитическим выражением.
Задание 1
Здесь даны задачи для освоения численных методов решения дифференциальных уравне-
ний эллиптического типа.
Задача 1.1. Найти приближенное решение уравнения
0
2
2
2
2
=
∂
∂
+
∂
∂
y
u
x
u
,
удовлетворяющее на окружности x
2
+y
2
=16 условию
u(x,y)
Г
=x
2
y
2
.
Точным решением является функция
])(256[
8
1
22222
yxyxu +−+= .
Задача 1.2. Найти приближенное решение уравнения Лапласа в квадрате с вершинами
А(0, 0), В(0, 1), С(1, 1), D(1, 0). Краевые условия приведены в таблице 1. Вычисления про-
водить с точностью 0,0001.
Таблица 1
№
u
AB
u
BC
u
CD
u
AD
1 30y 30(1-x
2
) 0 0
2 30y
30cos(πx/2) 30cos(πy/2)
0
3 50y(1-y
2
) 0 0
50sinπx
4 20y 20 20y
2
50x(1-x)
5 0 50x(1-x) 50y(1-y
2
) 50x(1-x)
6
30sinπy
20x 20y 30x(1-x)
7 30(1-y)
20
x
20y 30(1-x)
8
50sinπy
30
x
30y
2
50sinπx
9 40y
2
40 40
40sin((πx/2)
10 50y 50(1-x) 0
60x, 0≤x<1/2
60(1-x),
1/2≤x≤1

Задача 3.3. Найти приближенное решение уравнения Лапласа для единичного квадрата.
Краевые условия на левой стороне квадрата принять равными 2,5; 5,0; 7,5; 10,0; 7,5; 5,0; 2,5;
остальные краевые значения равны нулю. Вычислить с точностью 0,00001.
Задание 2
Задачи для освоения численных методов решения дифференциальных уравнений парабо-
лического типа.
Задача 2.1. Найти решение уравнения теплопроводности
2
2
x
u
t
u
∂
∂
=
∂
∂
при следующих начальных и краевых условиях
u(x,0)=4x(1-x) (0
≤
x
≤
1);
u(0,t)=0 , u(1,t)=0 (0
≤
t<
∞
) .
Таблица решения при h=1/10
j=0 j=1 j=2 j=3 j=4 j=5 j=6
i=0 0 0 0 0 0 0 0
i=1 0.360 0.347 0.336 0.326 0.317 0.309 0.302
i=2 0.040 0.627 0.613 0.600 0.588 0.576 0.564
i=3 0.840 0.827 0.813 0.800 0.787 0.774 0.761
i=4 0.960 0.947 0.933 0.920 0.907 0.894 0.881
i=5 1.000 0.987 0.973 0.960 0.947 0.934 0.921
j=0 j=1 j=2 j=3 j=4 j=5 j=6
i=6 0.960 0.947 0.933 0.920 0.907 0.894 0.881
i=7 0.840 0.827 0.813 0.800 0.787 0.774 0.761
i=8 0.640 0.627 0.613 0.600 0.588 0.576 0.564
i=9 0.360 0.347 0.336 0.326 0.317 0.309 0.302
i=10 0 0 0 0 0 0 0
Начальный столбец таблицы (j=0) заполняется на основании заданных начальных условий
u(x
i
,0)=4x
i
(1-x
i
)=0.4i(1-0.1i) (i=0, 1, 2, …,10) .
В первую (i=0) и последнюю (i=10) строки вписываются данные граничных условий
u(0, t
j
)=u(1, t
j
)=0 (j=0, 1, 2,… ).
Остальные столбцы j=0, 1, 2,… таблицы последовательно заполняются с помощью приме-
нения расчетной формулы (7.8). При этом можно учитывать симметрию искомой функции u.
Задача 2.2. Найти приближенное решение уравнения
2
2
x
u
t
u
∂
∂
=
∂
∂
,
удовлетворяющее условиям
u(x ,0)=sin
π
x (0
≤
x
≤
1) , u(0, t)=u(1,t)=0 (0
≤
t
≤
0.025).
Точным решением является функция u(x,t)=
xe
t
π
π
sin
2
−
.
Задача 2.3. Найти приближенное решение уравнения
tx
x
u
t
u
++
∂
∂
=
∂
∂
2
2
2
,
удовлетворяющее начальным и краевым условиям
u(x,0)=(1.1x
2
+1.5)sin
π
x , u(0,t)=0, u(1,t)=0 , 0
≤
t
≤
0.02.

Задача 2.4. Найти приближенное решение уравнения
xt
x
u
t
u
sin3
2
2
+
∂
∂
=
∂
∂
,
удовлетворяющее начальным и краевым условиям
u(x,0)=
x
e
5.0−
sin(
π
x/4) , u(0,t)=0, u(1,t)=
5.0−
e sin(
π
/4) , 0
≤
t
≤
0.02.
Задание 3
Задачи для освоения численных методов решения дифференциальных уравнений гипер-
болического типа.
Задача 3.1. Найти приближенное решение уравнения
2
2
2
2
x
u
t
u
∂
∂
=
∂
∂
,
удовлетворяющее граничным и начальным условиям
u(0,t)=u(
π
,t)=0 , (0
≤
t<
∞
);
u(x,0)=x(
π
-x) , u
t
(x,0)=0 (0
≤
x
≤π
) .
Таблица приближенных решений
t=0 t=h t=2h t=3h t=4h t=5h
x=0 0 0 0 0 0 0
x=h 0.518 0.487 0.426 0.366 0.305 0.244
x=2h 0.975 0.944 0.853 0.731 0.609 0.487
x=3h 1.371 1.340 1.249 1.097 0.914 0.731
x=4h 1.706 1.675 1.584 1.432 1.218 0.975
x=5h 1.980 1.950 1.858 1.706 1.493 1.218
x=6h 2.193 2.163 2.071 1.919 1.706 1.432
x=7h 2.346 2.315 2.224 2.071 1.858 1.584
x=8h 2.437 2.406 2.315 2.163 1.950 1.675
x=9h 2.467 2.437 2.346 2.193 1.980 1.706
Задача 3.2. Найти решение задачи
2
2
2
2
x
u
t
u
∂
∂
=
∂
∂
,
удовлетворяющее граничным и начальным условиям
u(x,0)=0.2x(1-x)sin
π
x , u
t
(x,0)=0 ,
u(0,t)=u(1,t)=0 .
Задача 3.3. Найти решение задачи
2
2
2
2
x
u
t
u
∂
∂
=
∂
∂
,
удовлетворяющее граничным и начальным условиям
u(x,0)=x(
π
-x) , u
t
(x,0)=0 ,
u(0,t)=u(
π
,t)=0 .
Библиография
1. Тихонов А.Н., Самарский А.А. Уравнения математической физики. -М.: Наука, 1964 - гл.
1, 4.
2.
Смирнов В.И. Курс высшей математики. -М.: Физматгиз, 1962. -т. 2. -гл. 7.
3.
Петровский И.Г. Лекции об уравнениях с частными производными. -М.: Физматгиз, 1961.
4.
Коллатц Л. Численные методы решения дифференциальных уравнений. -ИЛ, 1953.
5.
Милн В.Э. Численное решение дифференциальных уравнений. -ИЛ, 1955.
6.
Рябенький В.С., Филиппов А.Ф. Об устойчивости разностных уравнений. -М.: Гостехиз-
дат, 1956.
7.
Демидович Б.П., Марон И.А., Шувалова Э.З. Численные методы анализа. -М.: Наука,
1967.

Составитель: Ширапов Дашадондок Шагдарович
ОСНОВЫ ВЫЧИСЛИТЕЛЬНОЙ МАТЕМАТИКИ
Выпуск 6: Методы решения дифференциальных уравнений
с частными производными
Подписано в печать 16.04.2002 г. Формат 60×84 1/16.
Усл.п.л. 2,56, уч.-изд.л. 2,2. Тираж 100 экз. Заказ №64.
Издательство ВСГТУ. г.Улан-Удэ, ул. Ключевская, 40, а.
ВСГТУ, 2002 г.
