Ширапов Д.Ш. Основы вычислительной математики. Выпуск 6. Методы решения дифференциальных уравнений с частными производными
Подождите немного. Документ загружается.

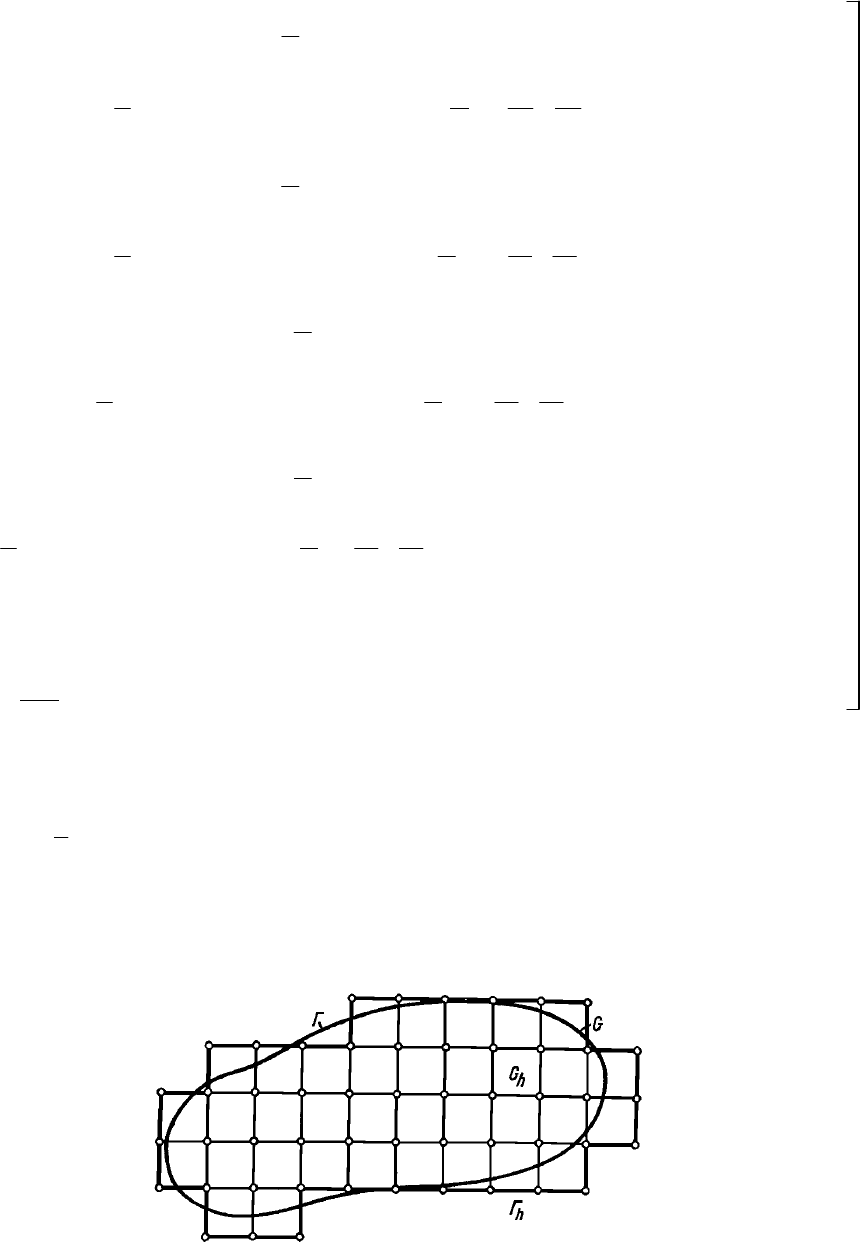
Вторая основная схема. Рассмотрим точки А(х, у), В(х-h, у+h), С(х+h, у+h), D(х+h, у-
h), Е(х-h, у-h), лежащие в центре и вершинах квадрата (рис. 10).
Как и в первой схеме, выразим значения функции и в точках В, С, D, Е через значения
этой функции и ее производных в точке А.
Полагая n=4 в формуле (4.3), получим:
u(x+h,y-h)= u(x,y)+h(u
x
– u
y
)+
!2
1
2
h (u
xx
-2u
xy
+ u
yy
)+
+
!3
1
3
h (u
xxx
-3u
xxy
+3u
xyy
- u
yyy
)+ +
),()(
!4
1
11
44
ηξ
u
yx
h
∂
∂
−
∂
∂
,
u(x-h,y-h)= u(x,y)+h(-u
x
– u
y
)+
!2
1
2
h (u
xx
+2u
xy
+ u
yy
)+
+
!3
1
3
h
(-u
xxx
-3u
xxy
-3u
xyy
- u
yyy
)+ + ),()(
!4
1
22
44
ηξ
u
yx
h
∂
∂
−
∂
∂
− , (4.8)
u(x-h,y+h)= u(x,y)+h(-u
x
+ u
y
)+
!2
1
2
h (u
xx
-2u
xy
+ u
yy
)+
+
!3
1
3
h (-u
xxx
+3u
xxy
-3u
xyy
+u
yyy
)+ + ),()(
!4
1
33
44
ηξ
u
yx
h
∂
∂
+
∂
∂
− ,
u(x+h,y+h)= u(x,y)+h(u
x
+ u
y
)+
!2
1
2
h
(u
xx
+2u
xy
+ u
yy
)+
+
!3
1
3
h (u
xxx
+3u
xxy
+3u
xyy
+u
yyy
)+ ),()(
!4
1
44
44
ηξ
u
yx
h
∂
∂
+
∂
∂
.
Складывая равенства (4.8), будем иметь
u(x+h,y-h)+u(x-h,y-h)+u(x-h,y+h)+ +u(x+h,y+h)=4u(x,y)+2
2
h
∆
u+О(h
4
),
откуда
∆
u=
2
2
1
h
[ u(x+h,y-h)+u(x-h,y-h)+u(x+h,y+h)+u(x-h,y+h)-4u(x,y)]+О(h
2
) .
Отбрасывая остаточный член О(h
2
), получаем, что уравнение Лапласа
∆
u=0 прибли-
женно можно заменить конечно-разностным уравнением
u(x,y)=
4
1
[ u(x+h,y-h)+u(x-h,y-h)+u(x+h,y+h)+u(x-h,y+h)].
5. Решение задачи Дирихле методом сеток
Идея метода сеток (или, метода конечных разностей) для численного решения краевых за-
дач для двумерных дифференциальных
уравнений заключается:
Рис. 11.
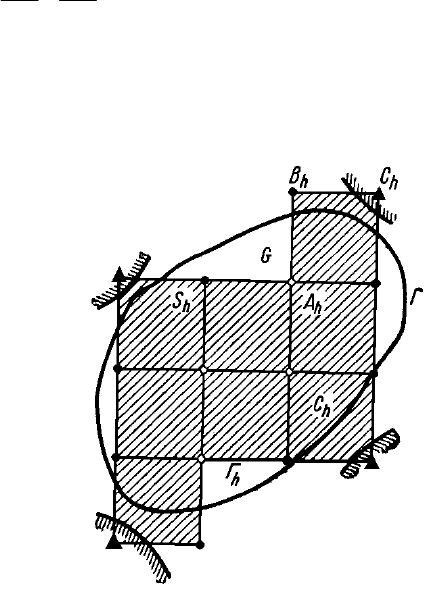
1) в плоской области G, в которой разыскивается решение, строится сеточная область G
h
,
состоящая из одинаковых ячеек (рис. 11) и приближающая данную область G;
2) заданное дифференциальное уравнение заменяется в узлах построенной сетки соответст-
вующим конечно-разностным уравнением;
3) на основании граничных условий устанавливаются значения искомого решения в гранич-
ных узлах области G
h
.
Решив полученную систему конечно-разностных уравнений, для чего решается система
линейных алгебраическую уравнений с большим числом неизвестных, мы найдем значения
искомой функции в узлах сетки, т. е. будем иметь численное решение нашей задачи.
Выбор сеточной области производится в зависимости от конкретной задачи, но во всех
случаях контур Г
h
сеточной области G
h
следует выбирать так, чтобы он как можно лучше
аппроксимировал контур Г заданной области G.
Сеточная область может состоять из квадратных, прямоугольных, треугольных и других
клеток. От выбора основного размера клетки h зависит величина остаточного члена R
h
при
замене дифференциального уравнения конечно-разностным. Следовательно, размер h тео-
ретически должен определяться требованием, чтобы этот оста-точный член был меньше по-
грешности, допустимой при решении. Однако такой путь не всегда целесообразен, так как
получаемый при этом размер h настолько мал и, следовательно, число клеток настолько ве-
лико, что решение оказывается практически невыполнимым.
Обычно задача решается сначала при большом значении h, т. е. при малом числе клеток,
и лишь после того, как задача грубо приближенно решена для этой крупной сетки, переходят
к более мелкой сетке или во всей рассматриваемой области, или в какой-нибудь ее части.
Покажем применение метода сеток для построения решения задачи Дирихле
2
2
2
2
y
u
x
u
∂
∂
+
∂
∂
=0 при (x,y)
∈
G и и(Р)=
ϕ
(Р) при P
∈
Г, (5.1)
где
ϕ
(Р)=
ϕ
(x,y) - заданная непрерывная функция, причем для простоты рассмотрим лишь
случай квадратной сетки. Будем предполагать, что область G ограничена простым замкну-
тым кусочно-гладким контуром Г.
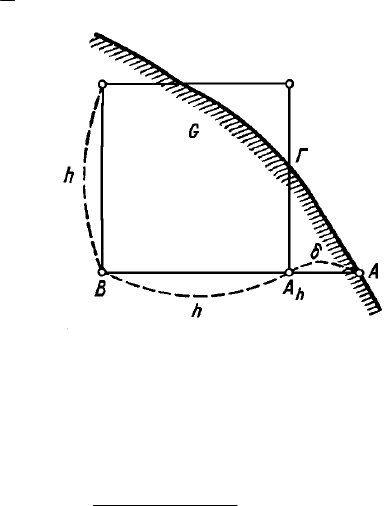
Рис. 12.

Выбрав шаг h, построим квадратную сетку
x
i
=x
o
+ih, y
j
=y
o
+jh (i, j=0, ±1, ±2, ...)
с таким расчетом, чтобы узлы (x
i
, y
j
) сетки S
h
или принадлежали области G, или отстояли
от ее границы Г на расстоянии меньшем, чем h.
Узлы сетки S
h
называются соседними, если они удалены друг от друга в направлении оси
Ох или оси Оу на расстояние, равное шагу сетки h. Узел A
h
сетки S
h
называется внутрен-
ним, если он принадлежит области G, а все четыре соседних с ним узла - множеству S
h
, в
противном случае он называется граничным (например, узлы В
h
и С
h
сетки S
h
) (на рис. 12
внутренние узлы обозначены светлыми кружками, а граничные -темными кружками и тем-
ными треугольниками).
Граничный узел сетки S
h
, называется узлом первого рода, если он имеет соседний внут-
ренний узел этой сетки (например, узел B
h
на рис. 12); в противном случае граничный узел
называется узлом второго рода (узел С
h
на рис. 12). Внутренние узлы и граничные узлы пер-
вого рода сетки S
h
называются расчетными точками. Граничные узлы второго рода не вхо-
дят в вычисление и могут быть изъяты из сетки S
h
(на рис. 12 граничные узлы второго рода
обозначены темными треугольниками).
Относительно сетки S
h
предположим, что множество ее расчетных точек «связное», т. е.
любые две расчетные точки можно соединить цепочкой узлов, каждые два смежных элемен-
та которой являются соседними узлами. Кроме того, будем считать многоугольную сеточ-
ную область G
h
выбранной так, чтобы ее геометрическая граница Г
h
, возможно ближе при-
мыкала к границе Г области G. Заметим, что узловые точки контура Г
h
могут лежать как
внутри, так и вне области G.
Значение искомой функции и=и(х,у) в точках (х
i
,у
j
) обозначим через u
ij
=u(х
i
,у
j
). Следуя
общей схеме, для каждой внутренней точки (х
i
,у
j
) сетки S
h
, заменяем дифференциальное
уравнение (5.1) конечно-разностным уравнением
u
ij
=
4
1
(u
i-1,j
+u
i+1,j
+u
i,j-1
+u
i,j+1
) , (5.2)
где (x
i±1
, у
j±1
) - расчетные точки.
В граничных узлах первого рода В
h
сетки S
h
полагаем
u(В
h
)=и(В)=
ϕ
(В), (5.3)
где В - ближайшая к В
h
точка границы Г.
Система (5.2) является неоднородной линейной системой, причем число неизвестных (т. е.
число внутренних узлов сетки) равно числу уравнений. Система (5.2) всегда совместна и
имеет единственное решение. Чтобы доказать это, достаточно убедиться в том, что соответ-
ствующая однородная система имеет лишь нулевое решение. Однородная система, очевидно,
формально может быть записана в виде системы (5.2), с той лишь разницей, что значение
функции
ϕ
(Р) на границе Г следует положить тождественно равным нулю:
ϕ
(Р)=0.
Однородная система (5.2) всегда совместна, так как эта система имеет тривиальное реше-
ние u
ij
≡
0.
Решив систему (5.2), получим приближенные значения искомой функции и=и(х,y) в уз-
лах сеточной области G
h
. Тем самым будет найдено приближенное численное решение за-
дачи Дирихле для области G
h
.
6. Метод Либмана
Если число узлов сетки S
h
велико, то непосредственное решение системы (5.2) становит-
ся затруднительным. Кроме того, для криволинейной области G значения функции и в гра-
ничных узлах сетки S
h
выбраны слишком грубо. Эти обстоятельства заставляют для реше-
ния указанной системы прибегать к итерационным методам с одновременным исправлением
граничных значений.
Согласно процессу усреднения Либмана, выбрав начальные приближения
)0(
ij
u , последова-
тельные приближения
)(k
ij
u
для внутренних узлов (x
i
,y
i
) сетки S
h
определяем по формуле
[]
)1(
1,
)1(
1,
)1(
,1
)1(
,1
)(
4
1
−
+
−
−
−
+
−
−
+++=
k
ji
k
ji
k
ji
k
ji
k
ij
uuuuu
(k=1,2, ...). (6.1)
Рис. 13.
Что касается граничных узлов А
h
сетки S
h
, то значения функции и(А
h
) в этих узлах после-
довательно исправляем по формулам линейной интерполяции:
u
(o)
(A
h
)=u(A)=
ϕ
(A) ,
u
(k)
(A
h
)=u(A)+
δ
δ
+
−
−
u
AuBu
k
)()(
)1(
, (k=1,2, …), (6.2)
где А - ближайшая к A
h
точка границы Г (u(А)==
ϕ
(A)), В - ближайший к A
h
внутренний
узел сетки S
h
(рис. 13) и
δ
- удаление узла A
h
, от точки А, причем
δ
>0, если A
h
- внутрен-
няя точка области G, и
δ
<0, если A
h
- внешняя точка области G. В частном случае, если
узел A
h
лежит на границе Г (A
h
≡
A,
δ
=0), то имеем точно
u
(k)
(A
h
)=u(A)=
ϕ
(A).
На практике после некоторого шага h можно считать u
(k)
(A
h
) неизменными (например,
если эти значения установятся с заданной точностью).
За начальные значения
)(o
ij
u теоретически можно взять любую систему чисел. Однако сле-
дует иметь в виду, что в силу принципа максимума для значений искомой функции и(х, у)
должны быть выполнены неравенства
m
≤
u
ij
≤
M ,
где границе Г: m=min
ϕ
(P) и M=max
ϕ
(P). Поэтому разумно полагать
m
≤
)(o
ij
u
≤
M .
В [1] и [3] доказаны, что для любого шага сетки h метод Либмана независимо от выбо-
ра начальных значений сходится, т. е. существует
ij
k
ij
k
uu =
∞→
)(
lim
, причем погрешность при-
ближенного решения имеет порядок O(h
2
).
Для оценки точности решения, полученного по методу сеток, существуют теоретические
оценки. Как правило, эти оценки весьма сложны и применение их затруднительно. Поэтому
на практике используют двойной пересчет решения с шагами h и 2h. Если соответствующие
результаты совпадают с заданной точностью, то считают, что искомое решение задачи най-
дено правильно. В противном случае применяют пересчет с шагом h/2 и сравнивают полу-
ченный результат с прежним результатом, соответствующим шаг h,
и т. д. Отдельно следует
проанализировать влияние ошибок округления. Схема вычислений должна быть устойчивой,
т. е. ошибки решения, связанные с округлением, не должны возрастать неограниченно.
7. Метод сеток для уравнения параболического типа
В качестве примера уравнения параболического типа рассмотрим уравнение теплопро-
водности для однородного стержня 0
≤
x
≤
l
2
2
2
x
u
a
t
u
∂
∂
=
∂
∂
,
(7.1)
где и=u(х,t) - температура и t - время. В дальнейшем для простоты будем полагать а=1 (к
такому случаю всегда можно прийти путем введения нового времени
τ
=a
2
t ).
Итак, рассмотрим уравнение
2
2
x
u
t
u
∂
∂
=
∂
∂
. (7.2)
Пусть в начальный момент времени t=0 задано распределение температуры u(x,0)=f(x) и
законы изменения температуры в зависимости от времени (тепловые режимы) на концах
стержня х=0 и x=l:
u(0,t)=
ϕ
(t) , u(l,t)=
ψ
(t) .
Требуется найти распределение температуры и=и(х,t) вдоль стержня в любой момент
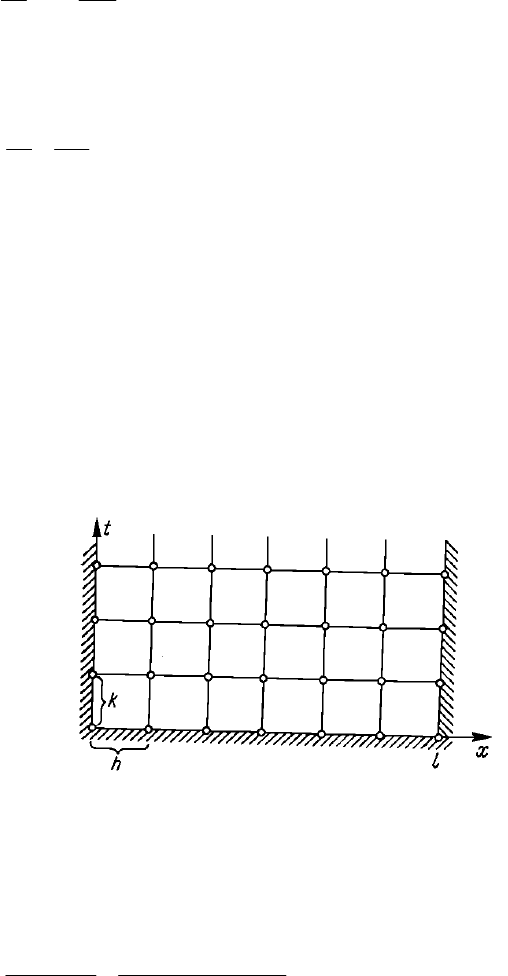
времени t. Решим эту смешанную задачу методом сеток [4, 5]. Для этого рассмотрим про-
странственно-временную систему координат (х ,t) (рис. 14). В полуполосе t
≥
0 , 0
≤
x
≤
l по-
строим прямоугольную сетку
x=ih (i=0, 1,…, n), t=jk (j=0, 1, 2,…),
где h=l/n (п - целое) - шаг вдоль оси Ох и k
2
=
σ
h
2
(
σ
-постоянная) - шаг вдоль оси Ot, вооб-
ще говоря, различны.
Рис. 14.
Величина
σ
будет выбрана ниже. Введя обозначения
x
i
=ih , t
j
=jk , u
ij
=u(x
i
, t
j
)
и заменяя уравнение (7.2) конечно-разностным уравнением, будем иметь
2
,1,1
2
1,
2
h
uuu
h
uu
jiijjiijji −++
+
−
=
−
σ
. (7.3)
Отсюда
u
i,j+1
=
σ
u
i-1,j
+(1-2
σ
)u
ij
+
σ
u
i+1,j
. (7.4)

Рис. 15.
Из рассмотрения формулы (7.4) ясно, что, зная значения функции и(х,t) в точках j-го слоя
t=jk , с помощью этой формулы можно вычислить значения и(х,t) в точках следующего
(j'+1)-го слоя t=(j+1)k (риc. 15). При вычислении пользуются четырьмя соседними узлами -
явная схема вида (рис. 15).
Таким образом, исходя из начального слоя t=0, значения и(х,t) для которого определяются
из начального условия
u(x
i
,0)=f(x
i
) , (i=0, 1,…, n),
и используя значения функции u(х,t) в крайних узлах (0, t
j
), (l, t
j
) (j=0, 1, 2,…), определяе-
мые граничными условиями
u(0,t
j
)=
ϕ
(t
j
) , u(l,t
j
)=
ψ
(t
j
) ,
по формуле (7.4) последовательно вычисляем:
u(x
i
,t
1
) , u(x
i
,t
2
) , u(x
i
,t
3
) ,… (i=0, 1,…, n),
т. е. находим значения искомой функции и(х,t) во всех узлах полуполосы.
Остается разумно выбрать величину
σ
. При этом будем исходить из требования, чтобы
ошибка при замене дифференциального уравнения (7.2) конечно-разностным уравнением
(7.3) была наименьшей.
Введем обозначения:
L[u]=
t
u
x
u
∂
∂
−
∂
∂
2
2
,
L
h
[u]=1/h
2
[(u
i+1,j
–2u
ij
+u
i-1,j
)-1/
σ
(u
i,j+1
–u
ij
)] ,
где L
h
[u] - конечно-разностный оператор, соответствующий дифференциальному операто-
ру L[и].
Разность
R
h
[u]= L
h
[u] - L[и] ,
называемая ошибкой аппроксимации, есть погрешность, которая получается при замене опе-
ратора L[и] оператором L
h
[u]. Вычислим эту погрешность в узлах (x
i
,t
j
) сетки для функции
и(х, у), являющейся решением уравнения (7.2). При этом L[и]=0 и
R
h
[u]= L
h
[u] . (7.5)
Учитывая, что
u
i+1, j
=u(x
i
+h,t
j
) , u
i-1, j
=u(x
i
-h,t
j
), u
i, j+1
=u(x
i
, t
j
+
σ
h
2
) ,
и разлагая L
h
[u] по формуле Тейлора в окрестности точки (x
i
, t
j
)
ограничиваясь членами
порядка h
6
, находим
L
h
[u]= +
∂
∂
+
∂
∂
+
∂
∂
+
∂
∂
+
4
4
4
3
3
3
2
2
2
2
!4!3!2
[(
1
x
u
h
x
u
h
x
u
h
x
u
hu
h
ijijijij
ij
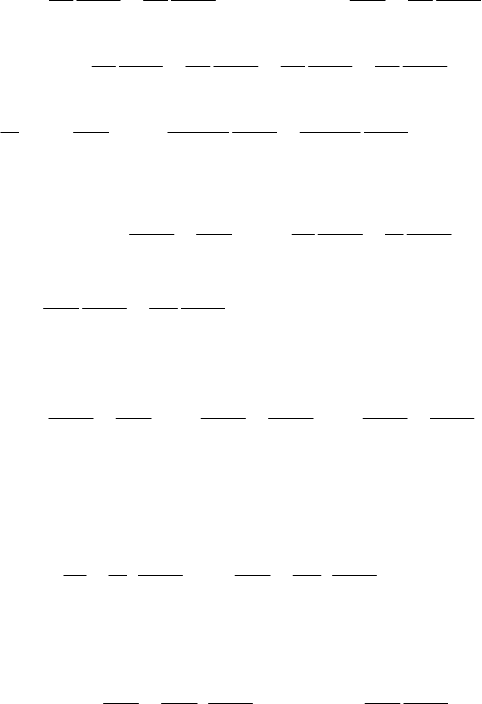
−
∂
∂
+
∂
∂
−+−
∂
∂
+
∂
∂
+
2
2
2
6
6
6
5
5
5
!2
2
!6!5
x
u
h
x
u
huu
x
u
h
x
u
h
ijij
ijij
ijij
−
∂
∂
+
∂
∂
−
∂
∂
+
∂
∂
− )
!6!5!4!3
6
6
6
5
5
5
4
4
4
3
3
3
x
u
h
x
u
h
x
u
h
x
u
h
ijijijij
)()]
!3
)(
!2
)(
(
1
6
3
3
32
2
2
22
2
hOu
t
u
h
t
u
h
h
t
u
u
ij
ijijij
ij
+−
∂
∂
+
∂
∂
+
∂
∂
+−
σσ
σ
σ
.
Отсюда после приведения подобных членов имеем
L
h
[u]= +
∂
∂
−
∂
∂
+
∂
∂
−
∂
∂
)
212
1
()(
2
2
4
4
2
2
2
t
u
x
u
h
t
u
x
u
ijijijij
σ
)()
6360
1
(
6
3
3
2
6
6
4
hO
t
u
x
u
h
ijij
+
∂
∂
−
∂
∂
+
σ
. (7.6)
Так как u(x,t) есть решение уравнения (7.2), то
t
u
x
u
ijij
∂
∂
=
∂
∂
2
2
,
2
2
4
4
t
u
x
u
ijij
∂
∂
=
∂
∂
,
3
3
6
6
t
u
x
u
ijij
∂
∂
=
∂
∂
.
Заменяя в (7.6) частные производные по t равными им частными производными по х ,
получим
L
h
[u]= )()
6360
1
()
212
1
(
6
6
6
2
4
4
4
2
hO
x
u
h
x
u
h
ijij
+
∂
∂
−+
∂
∂
−
σσ
. (7.7)
Выберем число
σ
так, чтобы первая скобка формулы (7.7) обратилась в нуль, т. е. положим
σ
/2=1/12 и, следовательно,
σ
=1/6. При этом значении
σ
будем иметь
L
h
[u]= )(
540
)()
216
1
360
1
(
6
6
6
4
6
6
6
4
hO
x
u
h
hO
x
u
h
ijij
+
∂
∂
−=+
∂
∂
− .
В силу (7.5) выполнено равенство R
h
[u]= L
h
[u] . Поэтому при таком выборе
σ
для погреш-
ности R
h
[u] получаем оценку R
h
[u]=О(h
4
), тогда как при другом выборе числа
σ
имеем
R
h
[u]=О(h
2
). В этом смысле значение
σ
=1/6 является для расчетной схемы 1 наилучшим.
Соответствующая расчетная формула (7.4) при таком выборе
σ
окончательно принимает
вид:
u
i, j+1
=1/6(u
i-1, j
+4u
ij
+u
i+1, j
) . (7.8)
Отметим, что оценка ошибки аппроксимации R
h
[u] в общем случае для граничных узлов (x
i
,
t
j
) не годится.
8. Метод прогонки для уравнения теплопроводности
Отметим, что для устойчивости конечно-разностной схемы для уравнения теплопровод-
ности шаги h=
∆
x
i
и k=
∆
t
j
должны быть неодинаковы, причем выбор шага h для простран-
ственной координаты х накладывает определенные ограничения на величину шага k для
временной координаты t. Важность этого обстоятельства была отмечена Курантом, Фрид-
рихсом и Леви. Так как при устойчивой схеме шаг k имеет порядок O(h
2
), причем отноше-
ние
σ
=k/h
2
ограничено сверху, то при малом h продвижение решения и(х ,t) по t весьма
незначительно и объем работы чрезвычайно велик. Например, приняв /г=0,1 и полагая
k=
σ
h
2
=1/600, получим, что для описания процесса распространения тепла за единичный
промежуток времени 0
≤
t
≤
1 требуется таблица, содержащая 600 строк!
Рассмотрим другую устойчивую вычислительную схему, для которой отношение k/h
2
не
является ограниченным сверху и поэтому шаг k=
∆
t
j
, временной координаты может быть
выбран сравнительно крупным.
Рассмотрим по-прежнему в области G{0
≤
х
≤
l , 0
≤
t<
∞
} приведенное уравнение теплопро-
водности
2
2
x
u
t
u
∂
∂
=
∂
∂
(8.1)
с граничными и начальными условиями
и(0, t)=
ϕ
(0) , и(l, t)=
ψ
(t), и (х, 0)=f(х). (8.2)
Построим в области G прямоугольную сетку
x
i
=ih (i=0, 1,…, n), t
j
=jk (j=0, 1, 2,…),
где h=l/п (п - целое) и k - некоторая положительная величина. Пусть и
ij
=u(x
i
,t
j
).
Используя приближенную симметричную формулу для второй производной по x и при-
меняя формулу численного дифференцирования по t «назад», для (j+1)-го слоя сетки вме-
сто дифференциального уравнения (8.1) будем иметь следующее конечно-разностное уравне-
ние:
k
uu
h
uuu
ijjijijiji
−
=
+−
+++++− 1,
2
1,11,1,1
2
, ,...)2,1,0;1,1( =−= jni ,
или
u
i-1, j+1
–(2+s)u
i,j+1
+u
i+1,j+1
=-su
ij
(8.3)
где s=h
2
/k.
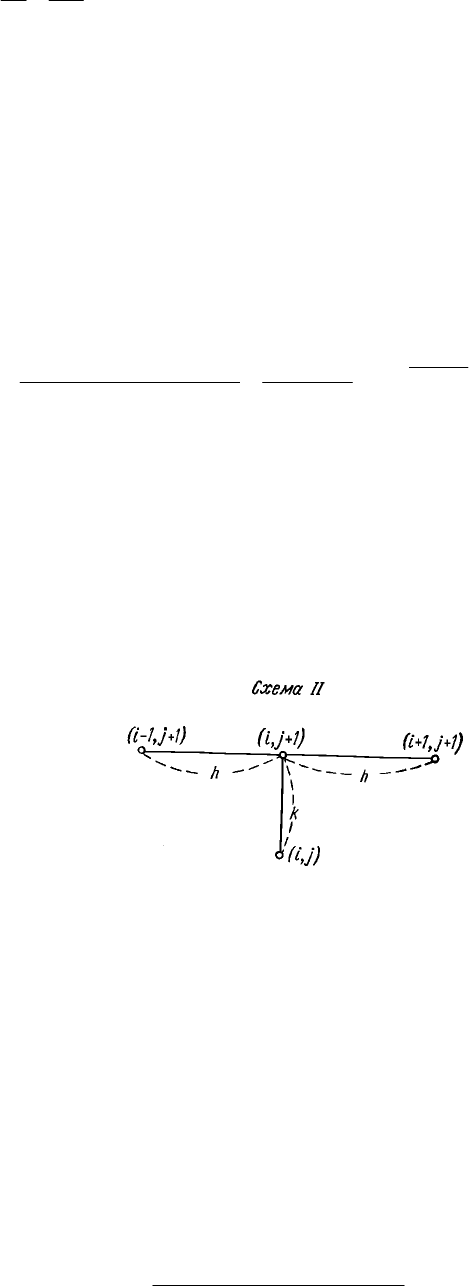
Таким образом, здесь использована схема 2 (неявная схема) (рис. 16).
Из граничных условий (8.2) получаем
u
o ,j+1
=
ϕ
(t
j+1
) , u
n ,j+1
=
ψ
(t
j+1
). (8.4)
Рис. 16.
Систему (8.3)-(8.4) будем решать методом прогонки. Пусть
)(
1,11,1,1, +++++
+
=
jijijiji
ubau (8.5)
и, следовательно,
)(
1,1,11,11,1 ++−+−+−
+
=
jijijiji
ubau (8.6)
Подставляя выражение (8.6) в формулу (8.3), будем иметь
ijjijijijiji
suuusuba
−
=
+
+
−
+
+++++−+− 1,11,1,1,11,1
)2()( ,
отсюда
1,1
1,11,11,1
1,
2
+−
+++−+−
+
−+
+
+
=
ji
jiijjiji
ji
as
usuba
u
.

Сравнивая это выражение с формулой (8.5), получим
1,1
1,
2
1
+−
+
−+
=
ji
ji
as
a
,
ijjijiji
subab
+
=
+−+−+ 1,11,11,
(8.7)
( i=2, 3,…, n ).
При i=1 из формул (8.3) и (8.5) имеем
jjjj
suuusu
11,21,11,0
)2(
−
=
+
+
−
+++
и
)(
1,21,11,11,1 ++++
+
=
jjjj
ubau . (8.8)
Отсюда, используя граничные условия, получаем
s
usut
u
jjj
j
+
+
+
=
++
+
2
)(
1,211
1,1
ϕ
. (8.9)
Так как формулы (8.8) и (8.9) должны быть тождественны, то, сравнивая их, выводим:
s
a
j
+
=
+
2
1
1,1
,
jjj
sutb
111,1
)(
+
=
++
ϕ
. (8.10)
Пользуясь формулами (7) и (10), производя «прогонку» в прямом направлении {прямой
ход), определяем две последовательности чисел:
1,11,21,1
,...,,
+−++ jnjj
aaa и
1,11,21,1
,...,,
+−++ jnjj
bbb .
Отсюда, применяя формулы (8.4) и (8.5), с помощью «обратного хода» находим значения
искомой функции:
)(
11, ++
=
jjn
tu
ψ
,
1,11,11,1,1
)(
+−+−++−
+=
jnjnjnjn
abuu ,
1,21,21,11,2
)(
+−+−+−+−
+=
jnjnjnjn
abuu ,
………………………….
1,11,11,21,1
)(
++++
+=
jjjj
abuu .
Таким образом, указан способ перехода от j-го слоя к (j+1)-му слою. Следовательно, от-
правляясь от известного начального (нулевого) слоя, можно шаг за шагом построить искомое
решение u(х,t) во всех точках сетки (х
i
,t
j
).
9. Метод сеток для уравнении гиперболического типа
Рассмотрим простейшее уравнение гиперболического типа, а именно уравнении свобод-
ных колебаний однородной ограниченной струны:
2
2
2
2
2
x
u
a
t
u
∂
∂
=
∂
∂
, (9.1)
и будем искать решение уравнения (9.1) при заданных начальных и краевых условиях
и(х, 0)=f(х), и
t
(х,0)=F(х) (0
≤
х
≤
l) (9.2)
и
u(0,t)=
ϕ
(t) , u(l,t)=
ψ
(t) (0
≤
t<
∞
) . (9.3)

Рис. 17.
Решим эту смешанную задачу методом сеток [5-7]. Как и в случае параболического урав-
нения, покроем полуполосу (0
≤
х
≤
l), (0
≤
t<
∞
) прямоугольной сеткой x
i
=ih (i=0, 1,…, n), t
j
=jk
(j=0, 1, 2,…), где
∆
x
i
=x
i+1
-x
i
=h=l/n (n – целое) и
∆
t
j
=t
j+1
-t
j
=k . На сетке x
i
, t
j
приближенно
заменим дифференциальное уравнение (9.1) соответствующим конечно-разностным уравне-
нием.
Пользуясь симметричными формулами для производных, будем иметь
2
,1,1
2
2
1,1,
22
h
uuu
a
k
uuu
jiijjijiijji −+−+
+
−
=
+
−
, (9.4)
При k=h/а уравнение (9.4) упрощается и принимает вид
u
i,j+1
+u
i,j-1
=u
i+1,j
+u
i-1,j
,
откуда
u
i,j+1
=u
i+1,j
+u
i-1,j
-u
i,j-1
. (9.5)
Из уравнения (9.5) видно, что для получения значений и(х,t) в (j+1)-м слое используются
значения и(х,t) в двух предыдущих слоях: j-м и (j-1)-м (рис. 17). Для начала вычисления по
формуле (9.5) также необходимо знать значения и(х,t) на двух слоях, в то время как началь-
ные условия (9.2) задают нам значения и(х,t) лишь на нулевом слое j=0. Однако, используя
начальные условия, можно определить значения и(х,t) на фиктивном слое с номером j=-1.
Для этого заменим производную во втором начальном уcловии конечно-разностным отно-
шением. Тогда будем иметь
i
ioi
F
k
uu
=
−
−
−1,
,
где F
i
=F(X
i
). Отсюда
u
i,-1
=u
io
–kF
i
. (9.6)
Теперь, зная значения и(х,t) на слое j=-1, определяемые с помощью формулы (9.6), можно
начать вычисления. Краевые условия (9.3) используются для получения значений u
oj
и u
nj
.
Вместо определения значений и(х,t) на слое j=-1 можно вычислить значения и(х,t) на
слое j=1. Это достигается, например, с помощью формулы Тейлора
2
2
2
1
2
t
u
k
t
u
kuu
ioio
ioi
∂
∂
+
∂
∂
+≈
. (9.7)
Учитывая, что согласно уравнению (9.1) имеем
2
2
2
2
2
x
u
a
t
u
ioio
∂
∂
=
∂
∂
,
перепишем формулу (9.7) в другом виде, а именно:
