Шевченко Т.Г., Мороз О.І., Тревого І.С. Геодезичні прилади
Подождите немного. Документ загружается.


40 Відомості з геометричної
оптики...
Порівнюючи (1.47) та (1.48), маємо
/ _ па
І па
(1.49)
Згідно з (1.40) і (1.41)
а
= —, а'
—- відповідно. Врешті
й;
одержимо
а а»
(1.50)
/ *
а о
Якщо у (1.49) замінити відношення — на — , отримаємо
а со
а
о)
(1.51)
або
пій)
=
пі'а/
(1.52)
Залежність (1.52) є інваріантною. Вона СВІДЧИТЬ, ЩО у
параксіальній області добуток показника заломлення п, розміру
предмета І та кута со променя з оптичною віссю у просторі
предметів дорівнює добуткові відповідних величин у просторі
зображень. Формулу (1.52) називають законом або інваріантом
Лангранжа-Гельмгольца (можна зустріти інваріант Гюйгенса-
Гельмгольца).
Інваріант є справедливим для двох та й для будь-якої
кількості поверхонь (рис. 1.24).
Рис. 1.24. Інваріант Лангража-Гельмгольца для декількох поверхонь
Згідно з (1.52) для двох поверхонь л,/,^ = п\1[о\;
= гі
г
і'
2
со
2
. Оскільки п
2
= п[, /
2
=
/]'
і
С0
2
~
Со[,
то

41 Відомості з геометричної
оптики...
пп
2
1
2
(02
= п
2
Ґ
2
а\, отже =
п[1[сс{
=
п
2
1
2
со
2
=
п
2
1'
2
(і)
2
,
або
П\1\Сі\ = п
2
1
2
а>
2
. Якщо ввести третю поверхню, то аналогічно
щі^ = ЩІ^Щ і т.ін., тобто інваріантність поширюється на будь-
яку кількість поверхонь. Треба відзначити, що зображення /,'
відрізка /
(
попередньої заломлювальної поверхні є предметом
для наступної заломлювальної поверхні. Наприклад, зображення
1[
відрізка , побудоване поверхнею 1, є предметом 1
2
для
поверхні 2 і т.п. Всі позначення п, І, со є подвійними
(п[ = п
2
;
1[
- Ґ
2
;
Щ
=
С0
2
).
Загальний інваріант Лангранжа-
Гельмгольца, що складається з т заломлювальних поверхонь,
має вигляд
= п
2
1
2
о^ =... =
п
т
І
т
(О
т
-
п'
т
І'
т
со'
т
.
(1.53)
1.3.6. Еквівалентна система з тонких лінз.
Телеоб'єктив
Найпростішою центрованою системою є лінза. Загалом у
лінзах є передня та задня головні площини і точки. Проте коли
товщина лінзи мала порівняно з її радіусами кривини, таку лінзу
називають тонкою. Головні площини в тонкій лінзі фактично збі-
гаються і перетворюються в її середню площину, яку й називають
головною. У геодезичних приладах використовують не поодинокі
лінзи, а їхні системи, що складаються з двох і більше лінз.
Рис. 1.25. Еквівалентна система з тонких лінз

42 Відомості з геометричної
оптики...
Частковим є випадок, коли система складається із збирної
Ц та розсіювальної Ь^ лінз (рис. 1.25). Таку систему лінз нази-
вають телеоб'єктивом, хоча зазвичай у телеоб'єктивах замість
поодинокої збирної лінзи використовують набір лінз, принаймні,
не менше ніж дві. Заміна набору лінз поодинокою збирною
лінзою правомірна і прийнята для спрощення.
Промінь світла 5, що поширюється з простору предметів
паралельно до оптичної осі системи 0\0
2
(тут О, - центр
збирної лінзи, 0
2
- центр розсіювальної лінзи), зустрічає збирну
лінзу і заломлюється її головною площиною у точці А.
Заломлений промінь мав би перетнути оптичну вісь у задньому
фокусі Р[ лінзи Ь]. Але, не досягнувши оптичної осі, він
потрапляє на лінзу заломлюється її головною площиною у
точці В і перетинає оптичну вісь у точці Р
е
. Лінза віддалена
від лінзи Ь[ на віддаль е < /', де /,' - задня фокусна віддаль
лінзи Ьу. Точка Р
е
розміщена на віддалі х від головної площини
лінзи Ь2. Внаслідок сумісної дії лінз Ц і Ц заломлений промінь
у просторі зображень поширюється у напрямку ВР^. Якщо
продовжити відрізок Р'
е
В, то його продовження перетне у про-
сторі предметів промінь 5 у точці С. Площину, що проходить
через точку С перпендикулярно до оптичної осі, можна уявити як
головну площину уявної збирної лінзи Ь
е
, яка заломила промінь
5 у точці С і спрямувала його у точку Р
е
, тобто свій задній
фокус. За своєю дією лінза Ь
е
еквівалентна дії системи лінз Ц і
Ь2 і її називають еквівалентною. Фокусна віддаль /
е
' лінзи Ь
е
дорівнює фокусній віддалі системи лінз Ц і . Щоб визначити
//, необхідно розглянути подібні трикутники ВО
г
Р'
х
і АО
х
Р[, а
д ^ Г / ' Г'
також СОР' і В0
2
Р' відповідно. = ——, а = —, але
В0
2
/{-е В0
2
х
АО^= СО, тому можна записати

43 Відомості з геометричної
оптики...
= (1.54)
/і ~е *
або
/;=-£-*. (і.55)
/і-е
Щоб визначити х, уявімо, що точка , яка звичайно роз-
ташована на оптичній осі, є джерелом випромінювання. Промінь
р'
е
В у зворотному ході променів після заломлення його лінзою
Ь
г
отримає напрямок В А, віддаляючись від оптичної осі, і дійсне
зображення точки Р
е
побудоване не буде. Проте його уявне
зображення розташується на перетині продовження променя АВ з
оптичною віссю, тобто у точці Р
х
. Згідно з формулою відрізків
(1.31), враховуючи зворотний напрямок променів
[а = -х; а = -(/{-е)] , отримаємо
1 1 1
!\~
е
Ї2
(1.56)
де /2 - фокусна віддаль лінзи Ц
3(1.56)
Х =
(1.57)
А+ІЇ-е
Підставивши значеннях з (1.57) у (1.55), маємо
Ґ = ——. (1.58)
^ Є
г' . г'
4
'
Ї\+Ї2~
е
Припущення у викладеному мають зміст, коли (/]'-<?) < |./2І
•
В описаній оптичній системі головна задня площина уявної
лінзи Ь
е
винесена вперед у простір предметів за межі системи,
тому еквівалентна задня фокусна віддаль /
е
' більша за віддаль е

44 Відомості з геометричної
оптики...
між передньою заломлювальною поверхнею і площиною зобра-
ження, тобто більша від довжини самої оптичної системи. В
оптичних системах геодезичних приладів, зокрема у зорових
трубах з внутрішнім фокусуванням, це дає змогу створювати
короткі труби з великою фокусною віддалю. Щоправда, замість
збирної лінзи Ц застосовуються складні об'єктиви, а за
розсіювальну лінзу Ьі слугують фокусувальні компоненти, що
найчастіше являють собою дві склеєні лінзи.
Коли ціль, на яку візують зорову трубу, розташована у
просторі предметів у нескінченності, зображення її фокусується у
задній фокусній площині телеоб'єктива, яка проходить через
точку Р^
•
Проте коли ціль не розташована у нескінченності, а
візувати доводиться на точки, що розміщені на різних віддалях
від зорової труби, зокрема в декількох десятках метрів і ближче,
телеоб'єктив будує зображення не у задній фокусній площині, а
поблизу неї (такі спостереження зазвичай виконують під час
інженерно-геодезичних вимірювань). Для того, щоб зображення
завжди формувалось у незмінному положенні задньої фокусної
площини телеоб'єктива, фокусувальний компонент роблять
рухомим. Внаслідок переміщення лінзи (рис. 1.25) віддаль е
між лінзами і змінюється, а лінза перемішуючись,
змінює у незначних межах задню фокусну віддаль і спрямовує
заломлений промінь у те саме положення точки Р'
е
.
Отже, у
зорових трубах із внутрішнім фокусуванням створюється
можливість постійно формувати зображення в одній і тій самій
площині незалежно від віддалі до візирної цілі.
1.4. Недоліки (аберації) оптичних систем
Одержані основні залежності та описані властивості оптич-
них систем є цілком справедливі для параксіальних пучків та
ідеальних оптичних систем. Крім того, було прийнято, що світло
є монохроматичним, а показник заломлення середовища не
залежить від довжин хвилі світла.

45 Відомості з геометричної
оптики...
У реальних оптичних системах, що створюються у геоде-
зичних приладах, все значно складніше. Надто вузький парак-
сіальний пучок променів не завжди забезпечує достатню освіт-
леність зображень, білий промінь світла може зазнати дисперсії.
У геодезичних приладах застосовують оптичні системи, що
мають доволі значні відносні отвори. Це може призвести до
порушення гомоцентричності пучків у просторі зображень, а самі
зображення можуть мати порушення подібності і недостатню
чіткість, тобто проявляються недоліки або аберації оптичних
систем. Знання фізичної сутності аберацій дає змогу розробити
заходи для послаблення їхнього впливу у візуальних оптичних
системах, для яких найнебезпечнішими є осьові аберації, що
спотворюють зображення точок на оптичній осі. Такими є
сферична і хроматична аберації.
1.4.1. Сферична аберація
Промені, що йдуть від точки А (рис. 1.26) або паралельно до
оптичної осі потрапляють широким пучком на сферичну
заломлювальну поверхню, наприклад, лінзи. Промені пучка, що
віддаленіші від оптичної осі, мають властивість заломлюватися
сильніше ніж промені, що мають невеликий кут з віссю.
Внаслідок цього всі заломлені лінзою промені не зберуться в
одній точці. Властивість лінз порушувати стигматичність
зображення називають сферичною аберацією. На рис. 1.26
замість однієї точки А^, у просторі зображень утворилась
множина таких точок: від А^ до Д-. Якщо у точці Ац встановити
перпендикулярно до оптичної осі екран, на ньому вийде
зображення нечіткої плями радіуса р
с
. Щодо паралельного
пучка променів, то параксіальні промені зберуться у задньому
фокусі р', а крайні - у точці Р- , яка розташована ближче до
лінзи. Величину Д/
с
' = /•'- /' називають поздовжньою сферич-
ною аберацією, а р
с
- поперечною.

46
Відомості з геометричної
оптики...
А
-З
Рис. 1.26. Сферична аберація лінзи
Для лінзи у першому наближенні поздовжню та поперечну
сферичну аберацію можна обчислити згідно із залежностями
відповідно.
У залежностях (1.59) і (1.60): г - радіус вхідного отвору,
/' - фокусна віддаль, К - коефіцієнт, що залежить від показ-
ника заломлення скла та радіусів кривини сферичних поверхонь.
Відповідно до залежностей (1.59) і (1.60) поздовжня та попе-
речна сферична аберація зростають із збільшенням вхідного от-
вору, зменшенням /' або радіусів кривини поверхонь лінз.
Вплив сферичної аберації зменшують, застосовуючи діаф-
рагми, наприклад, зменшення вхідного отвору вдвічі зменшує
сферичну поперечну аберацію у вісім разів. Крім діафрагмування,
застосовують комбінації із збирних та розсіювальних лінз різних
радіусів кривини та з різних сортів та марок скла.
1.4.2. Хроматична аберація
Сукупність променів, що поширюються в однорідному се-
редовищі, справляє на око враження білого світла. Після пере-
ходу з одного прозорого оптичного середовища до іншого, яке
(1-59)
(1.60)
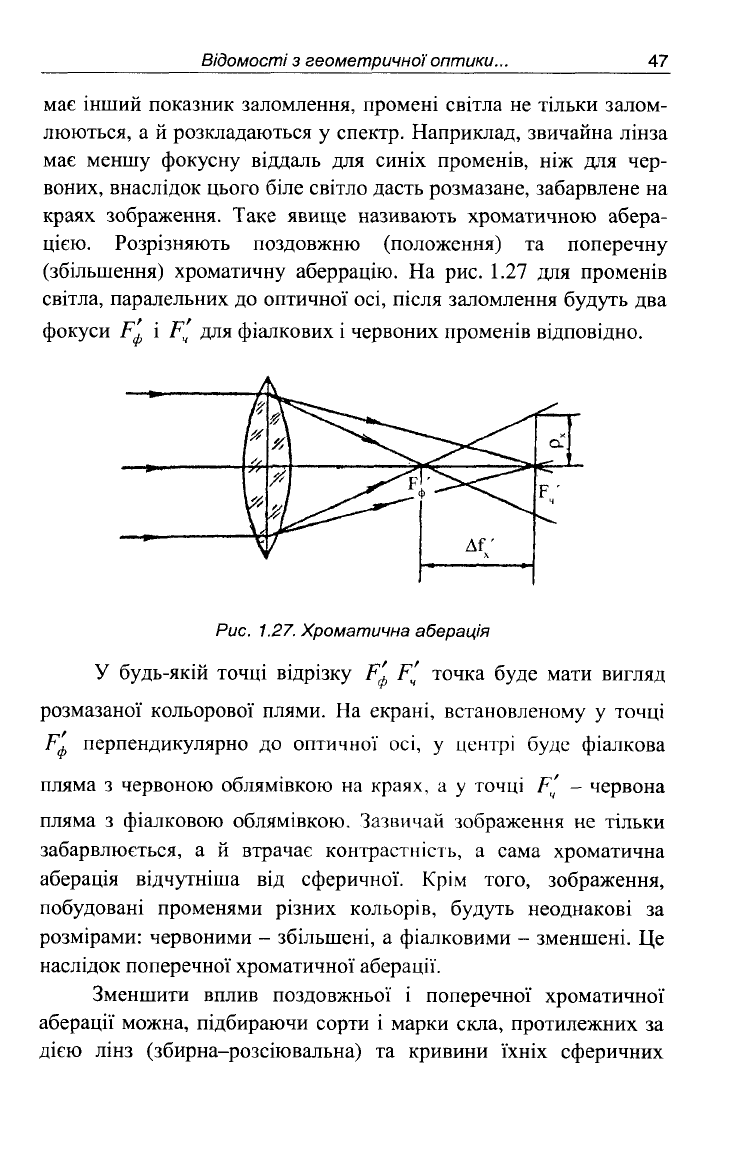
47 Відомості з геометричної
оптики...
має інший показник заломлення, промені світла не тільки залом-
люються, а й розкладаються у спектр. Наприклад, звичайна лінза
має меншу фокусну віддаль для синіх променів, ніж для чер-
воних, внаслідок цього біле світло дасть розмазане, забарвлене на
краях зображення. Таке явище називають хроматичною абера-
цією. Розрізняють поздовжню (положення) та поперечну
(збільшення) хроматичну аберрацію. На рис. 1.27 для променів
світла, паралельних до оптичної осі, після заломлення будуть два
фокуси Г' і Р'
ч
для фіалкових і червоних променів відповідно.
г А
А
оГ.
ґ
'\
%
>
ДГ'
X
р;
Рис. 1.27. Хроматична аберація
У будь-якій точці відрізку Р'
ф
Р'
ч
точка буде мати вигляд
розмазаної кольорової плями. На екрані, встановленому у точці
Рф перпендикулярно до оптичної осі, у центрі буде фіалкова
пляма з червоною облямівкою на краях, а у точці Р'
{
- червона
пляма з фіалковою облямівкою. Зазвичай зображення не тільки
забарвлюється, а й втрачає контрастність, а сама хроматична
аберація відчутніша від сферичної. Крім того, зображення,
побудовані променями різних кольорів, будуть неоднакові за
розмірами: червоними - збільшені, а фіалковими - зменшені. Це
наслідок поперечної хроматичної аберації.
Зменшити вплив поздовжньої і поперечної хроматичної
аберації можна, підбираючи сорти і марки скла, протилежних за
дією лінз (збирна-розсіювальна) та кривини їхніх сферичних

48
Відомості з геометричної
оптики...
поверхонь. Принцип дії лінз, підібраних за наведеними вище
умовами, показано на рис. 1.28. (передня лінза 1 з крона, а задня
лінза 2 з флінта).
І*
V/
Рис. 1.28. Система лінз,
що послаблює хроматичну аберацію
Промінь, пройшовши систему, вийде з неї білим. Системи
лінз, що усувають аберацію для двох кольорів спектра, називають
ахроматичними, а ті, що усувають вторинний спектр, апохро-
матичними. Далі йдуть надапохроматичні системи, які дуже
дорогі та трудомісткі. Зорові труби сучасних геодезичних при-
ладів зазвичай апохроматичні.
1.4.3. Кома, астигматизм, дисторсія
Якщо промені спрямовуються в оптичну систему широким
пучком під кутом до оптичної осі з точки, що не лежить на осі,
симетрія заломлення відносно центрального променя може бути
порушена. На екрані буде зображення точки у вигляді плями
нерегулярної форми, подібної до коми. Кому виправляють
підбором діафрагм та лінз різної кривини із різних сортів та
марок скла. Оптичні системи, що усувають сферичну аберацію,
включаючи кому, називають апланатичними.
Вузькі пучки променів, що поширюються від точок, які не
розташовані на оптичній осі, після заломлення зазвичай відобра-
жаються астигматично, оскільки промені проходять заломлю-
вальну сферичну поверхню оптичної системи за різних умов. У
меридіональній площині промені заломлюються сильніше ніж у
перпендикулярній до неї сигітальній площині. Внаслідок цього
точки з меридіональної площини у сигітальній площині будуть

49 Відомості з геометричної
оптики...
зображатися лініями або витягнутими еліпсами. Точки сигіталь-
ної площини аналогічно відображаються у меридіональній
площині. Астигматизм виправляють, підбираючи радіуси криви-
ни заломлювальних поверхонь, їхні фокусні віддалі та товщини
лінз. Оптичні системи, в яких астигматизм усунений, називають
анастигматами.
Порушення геометричної подібності зображення та пред-
мета у спряжених площинах, перпендикулярних до оптичної осі,
називають дисторсією. Причиною дисторсії є змінне поперечне
збільшення /5 у полі зору оптичної системи. Внаслідок цього
зображення квадрата буде за формою як подушка (рис. 1.29, б)
або бочкоподібним (рис. 1.24, в). Зменшення дисторсії досягають
встановленням діафрагм, підбором лінз різної товщини та
радіусів.
Рис.
1.29.
Дисторсія: а - зображення, не спотворене дисторсією;
б - додатна дисторсія; в - від'ємна дисторсія
