Shen S., Tuszynski J.A. Theory and Mathematical Methods for Bioformatics

Подождите немного. Документ загружается.

384 13 Morphological Features of Protein Spatial Structure

Based on the diagram in Fig. 13.9, if point d is not in O(δ), and sphere

O(δ, d) does not contain any points in A

, then the small sphere O[r(δ)]

can enter from the triangle δ and arrive at point d without encountering

any points in A

.Soγ

(d) ≥ r(δ) holds. On the other hand, γ

(d) cannot

be greater than r(δ), therefore, γ

(d)=r(δ) holds. Thus ends the proof

of the theorem.

2. For a ﬁxed convex hull V

(3)

, and for each boundary triangle with δ ∈ V

(3)

we can get set B(δ) by (13.13). These sets might intersect, so:

(a) Let B =

δ∈ V

(3)

B(δ), so for each d ∈ B there always exists

agroup

= {δ

,δ

, ··· ,δ

}⊂V

(3)

,k≥ 1

such that for any δ ∈ V

, d ∈ S(δ) holds, and for any δ ∈ V

(3)

− V

point d is not in B(δ).

(b) Based on point d and V

in condition (a), we get γ

(d)=γ

(d),

i =1, 2, ··· ,k,thus

γ(d)=max{γ

(d), where i =1, 2, ··· ,k} (13.14)

is the γ-function of point d.

in (13.14), such

that d ∈ B(δ

), and γ(d)=γ

(d) holds. We call δ

the approaching

triangle of point d.

13.4.2 Recursive Calculation of γ-Function

In above section, we have calculated the γ-function of all points in set B by

the 0-level convex hull V

(3)

. To calculate the γ-function of other points, we

introduce the following recursive steps:

1. We consider each triangle δ on a 0-level convex hull V

(3)

as a directed

triangle. For each d ∈ B, we denote its approaching triangle by δ

δ(a

), and denote a tetrahedron with four vertices a

,d by

Σ(a

,d). Sphere O(a

,d) does not contain any points in A −

,d}; this implies that Σ(a

,d) does not contain any points

in A −{a

,d}. Thus we can retract the directed polyhedron V

(3)

according to (d, δ

), d ∈ B, to get a new directed polyhedron V

(3)

2. For each boundary triangle δ ∈ V

(3)

in the directed polyhedron V

(3)

,we

can deﬁne set B



(δ) as in (13.13) and the γ-function of each point in this

set about this triangle.

3. Similar to (13.14), we can calculate the γ-function of each point in set



(δ). We repeat this to get the γ-function of each point in set A.

13.4 Recursive Algorithm of γ-Function 385

Table 13.5. Distribution of set A

in O(δ

)interior

12 12 12 12 12 12 12 12

1 17.6747 2 28.0649 3 ∞ 4 134.445 5 56.1087 6 ∞ 7 ∞ 8 31.2947

9 34.3887 10 17.6422 11 33.5496 12 14.4538 13 31.5049 14 11.8489 15 19.0867 16 10.1349

17 35.2943 18 7.74091 19 310.286 20 6.89257 21 97.6989 22 5.92052 23 146.656 24 9.07193

25 ∞ 26 ∞ 27 183.222 28 5.22915 29 19.4598 30 15.7119 31 5.16211 32 8.29965

33 10.577 34 10.6558 35 8.04309 36 46.9502 37 171.338 38 8.77772 39 8.0484 40 8.59963

41 14.8524 42 9.84345 43 31.3584 44 31.5786 45 32.2711 46 14.1265 47 17.7637 48 15.7874

49 23.9796 50 13.0015 51 ∞ 52 ∞ 53 ∞ 54 110.071 55 62.6285 56 12.2717

57 22.635 58 10.1757 59 41.7513 60 10.0418 61 51.5585 62 10.8136 63 21.8588 64 8.88514

65 16.496 66 6.8638 67 16.8678 68 12.9889 69 10.7766 70 ∞ 71 ∞ 72 ∞

73 ∞ 74 19.4956 75 18.6084 76 52.7615 77 13.7498 78 11.1552 79 11.9087 80 17.6727

81 34.1265 82 9.52151 83 9.66642 84 53.1736 85 18.096 86 94.8295 87 34.2828 88 56.8256

89 11.8952 90 20.7947 91 51.1955 92 29.9013 93 ∞ 94 6.47052 95 11.0615 96 50.5705

97 8.99533 98 63.0856 99 55.9255 100 9.11707 101 9.40965 102 10.549 103 4.98585 104 6.83729

105 4.84028 106 6.04947 107 12.3899 108 5.7534 109 4.99202 110 13.2468 111 10.0297 112 5.08576

113 10.0886 114 12.4667 115 5.66732 116 8.98487 117 9.30359 118 8.80155 119 5.55789 120 8.77183

121 8.51864 122 6.3084 123 6.8501 124 10.5035 125 9.8508 126 7.40003 127 5.22846 128 4.89868

129 4.62161 130 4.99202 131 8.07632 132 8.55018 133 6.12883 134 14.5463 135 60.1815 136 4.61216

137 50.3308 138 7.42384 139 19.628 140 11.3168 141 10.4905 142 15.084 143 9.01234 144 73.9075

145 318.287 146 36.0357 147 ∞ 148 ∞ 149 79.3614 150 15.9595 151 20.142 152 9.92854

153 17.0891 154 7.74252 155 39.2583 156 5.70074 157 63.0932 158 4.83674 159 325.22 160 ∞

161 26.3831 162 ∞ 163 111.59 164 ∞ 165 15.038 166 7.25092 167 11.3238 168 9.01574

169 4.93283 170 4.83674 171 14.2906 172 ∞ 173 150.963 174 288.489 175 14.52 176 47.1928

177 7.85079 178 67.5936 179 7.95977 180 29.3243 181 14.1467 182 ∞ 183 ∞ 184 13.2111

185 32959.8 186 7.87724 187 ∞ 188 6.93986 189 286.936 190 8.31956 191 86.0665 192 13.1293

193 63.7394 194 12.0244 195 115.449 196 4.79312 197 15.0236 198 ∞ 199 64.5202 200 4.24766

386 13 Morphological Features of Protein Spatial Structure

Table 13.5. (continued)

12 12 12 12 12 12 12 12

201 16.5668 202 ∞ 203 14.6863 204 608.19 205 5.88999 206 5.19302 207 ∞ 208 ∞

209 ∞ 210 483.284 211 4.75501 212 30.9646 213 5.81223 214 23.4438 215 10.2305 216 53.6861

217 6.62237 218 ∞ 219 8.30546 220 ∞ 221 14.3289 222 20.4224 223 ∞ 224 11.8745

225 ∞ 226 9.0402 227 457.683 228 7.35689 229 224.537 230 6.13938 231 158.361 232 20.5498

233 84.368 234 7.81338 235 84.225 236 4.62738 237 4.99202 238 5.94237 239 10.2674 240 10.0224

241 11.6428 242 5.90806 243 13.668 244 ∞ 245 ∞ 246 392.226 247 18.3927 248 10.7555

249 4.93617 250 4.24766 251 5.06028 252 10.7187 253 30.9887 254 5.42648 255 334.932 256 4.99202

257 132.451 258 4.98836 259 192.262 260 5.21359 261 ∞ 262 7.54876 263 ∞ 264 9.99908

265 ∞ 266 ∞ 267 ∞ 268 7.93322 269 82.7797 270 8.40605 271 59.3073 272 5.66904

273 ∞ 274 9.69061 275 275.624 276 5.50547 277 28.7123 278 5.26492 279 15.7718 280 5.06028

281 79.8257 282 ∞ 283 5.26597 284 26.0141 285 ∞ 286 97.967 287 ∞ 288 ∞

289 10.1641 290 14.561 291 8.14075 292 7.47297 293 10.5766 294 9.1374 295 414.723 296 5.13234

297 ∞ 298 11.6084 299 28.409 300 7.83004 301 42.8329 302 8.8507 303 ∞ 304 ∞

305 28.2231 306 46.4136 307 34.7497 308 8.635 309 50.7039 310 8.48863 311 68.7925 312 4.7766

313 35.915 314 5.55789 315 ∞ 316 8.40479 317 ∞ 318 8.84927 319 ∞ 320 ∞

321 ∞ 322 8.1585 323 16.3929 324 5.51516 325 10.0118 326 8.88307 327 7.81688 328 6.54123

329 22.51 330 14.588 331 6.05049 332 24.096 333 6.09214 334 125.563 335 7.42444 336 1845.54

337 8.43237 338 281.116 339 10.5048 340 28.9558

In the header 1 represents the serial number of the atom, and 2 represents the value of γ-function of the atom

13.5 Proof of Relative Theorems 387

13.4.3 Example

We still use the protein E. coli OmpF porin as an example. On the basis of

Tables 12.6, 13.1, and 13.2, we calculate the γ-function of the C

atoms in

each amino acid, and ﬁnally ﬁnd the values of the γ-function of all C

atoms

in this protein, which are shown in Table 13.5.

13.5 Proof of Relative Theorems and Reasoning

of Computational Formulas

13.5.1 Proofs of Several Theorems

ProofofTheorem43

If a ∈ A is a zero-depth point in A, then there exists a plane Π through

point a such that all points in A lie on the same side of Π.Drawatangent

sphere of plane Π through point a. If this tangent sphere lies on the other

side of plane Π, and is outside of Ω(A) for any radius γ>0, point a is always

the γ-accessible radius point of A for any γ>0.

Conversely, if point a is always the γ-accessible radius point of A for any

γ>0, then a must be the zero-depth point in A. We prove this using contra-

diction; if a is not the zero-depth point in A, then there always exist points of

A on both sides of plane Π which is through point a. The following properties

would then hold:

1. Let E be a rectangular coordinate system where origin a, k is the unit

vector, its polar angle is (ψ,θ). Here (ψ,θ) changes by region:

Ψ × Θ = {(ψ,θ): 0 ≤ ψ ≤ 2π, 0 ≤ θ ≤ π} . (13.15)

Denote a neighborhood of (ψ,θ

)by

k(ψ, θ)={k



=(ψ



,θ



): (ψ



−ψ)

+(θ



−θ)

<(k),(k) > 0} . (13.16)

2. Let N

be a normal plane which is through point a,withk as its vector. N

separates set A into sets, which we denote by A

(k),A

(k), respectively.

Both sets are nonempty sets. Without loss of generality, we always adopt

1 ≤||A

(k)|| ≤ ||A

(k)||.

From geometric properties, we realize that there must exist a suﬃciently

small (k) >θ>0, for any k



∈ k(ψ, θ), the two sets divided by its normal

plane N



are denoted by A

(k),A

(k). There also exists a suﬃciently

large γ(k) > 0 such that the normal plane N

is a tangent plane and a

is a tangent point. If the spheroid with radius γ(k)isonthetwosidesof

the normal plane N

,theycontainsetA

(k)andA

(k), respectively.

388 13 Morphological Features of Protein Spatial Structure

3. Ψ ×Θ is covered by all the small regions k(ψ, θ)ifk is changing in Ψ ×Θ.

Since Ψ × Θ is a compact region in Euclidean space, it follows from the

theorem of limited coverage in topological space that there must exist

ﬁnite spheres as follows:

=(ψ

,θ

) , k

=(ψ

,θ

) , ··· , k

=(ψ

,θ

) , (13.17)

such that corresponding neighborhoods

k(ψ

,θ

), k(ψ

,θ

), ··· , k(ψ

,θ

) (13.18)

cover the region Ψ ×Θ.

4. By property 2, for each k

, i =1, 2, ···,m, there exists a suﬃciently large

γ(k

) > 0 such that the sphere with radius γ(k

) is tangent to the normal

plane N

at point a, and this sphere contains the set A

). Let

=max{γ(k

),γ(k

), ··· ,γ(k

)} (13.19)

5. For an arbitrary sphere through point a with radius γ>γ

,wedenoteit

by O(a, γ). Let Π be its tangent plane through point a and let k be its

normal vector. Then, there is a i ∈{1, 2, ··· ,m} such that Π ∈ k(ψ

,θ

)

and sphere O(a, γ)containssetA

)orsetA

). Therefore, point a

could not be the γ-accessible radius point. Hence, the theorem holds.

Proof of Theorem 44

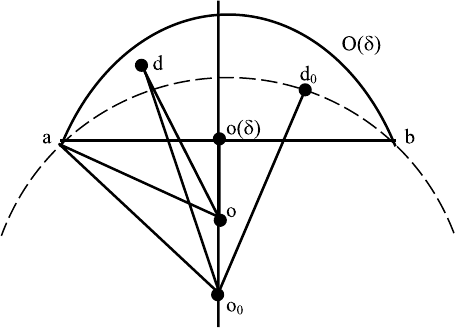
For the ﬁrst proposition in Theorem 44, we consult Fig. 13.10 and prove

it. In this ﬁgure, the bold straight line represents triangle δ, the bold circle

represents the sphere O(o(δ),r(δ)) generated by triangle δ. d, d

are the points

in O(o(δ),r(δ)), on the same side of the triangle δ,ando, o

represent the

Fig. 13.10. Proof of Theorem 44, proposition 1

13.5 Proof of Relative Theorems 389

centers of O(δ, d), O(δ, d

), respectively. To prove that d

= d



,wemust

prove:

1. If |o

o(δ)|≥|oo(δ)|,then|d

|≥|do| holds.

2. Conversely, if |d

|≥|do|,then|o

o(δ)|≥|oo(δ)| holds.

Without loss of generality, we may assume that points d and d

lie in two

semispheres of O(o(δ),r(δ)). Following from the deﬁnition of o, o

, we realize

|oa| = |ob| = |od| , |o

a| = |o

b| = |o

| .

We compare the two triangles δ(a, o(δ),o

)andδ(a, o(δ),o). Both of them are

right triangles, having the common edge ao(δ). The edge of sphere o(δ)o and

the edge of o(δ)o

are collinear, thus, |o

o(δ)|≥|oo(δ)| holds if and only if

|ad

| = |d

|≥|ao| = |do| .

Therefore, |o

o(δ)|≥|oo(δ)| is equivalent to |o

|≥|od|; namely, the deﬁni-

tions of d

and d



are equivalent, and d

= d



holds. The ﬁrst proposition in

Theorem 44 has been proven.

We consult Fig. 13.10 to prove the second proposition in Theorem 44.

We compare the two triangles δ(a, o, o

)andδ(d, o, o

). Since oo

is their

common edge, and |od| = |oa| holds, it follows that these two triangles have

two equivalent edges. On the other hand, following from the deﬁnition of

o(δ),o,o

and the inequality



doo



aoo

,wehavethat|do

| > |ao

| (in

a triangle, a larger angle corresponds to a larger edge). Thus, point d must

be outside of the sphere O(a, b, cd

). Proposition 1 in Theorem 44 is now

proven.

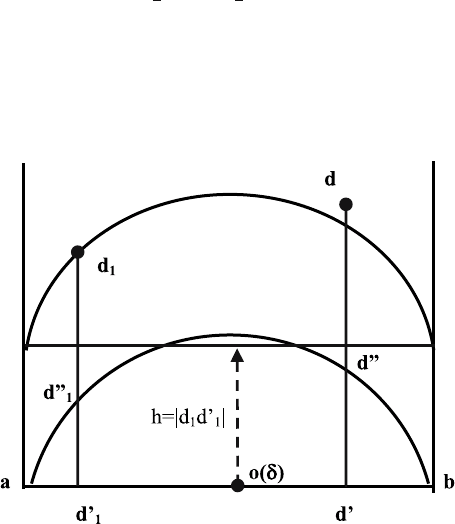
To prove proposition 2 in Theorem 44 as shown in Fig. 13.11, we can

project each point in Q(δ, A

)toπ(δ)ifA

(δ)isconvexandQ(δ, A

)is

Fig. 13.11. Illustration of the proof of Theor. 44 (2)

390 13 Morphological Features of Protein Spatial Structure

a nonempty set. Furthermore, if d

is the point such that |d



| is the min-

imum of |dd



|, d ∈ Q(δ, A

), we only need to move the small sphere O(δ)

vertically upwards. If the moving distance is |d



|, then the small sphere

encounters point d

but does not encounter any points in Q(δ, A

); thus, it

does not encounter any points in A

. Therefore, γ(d

)=r(δ) holds, and the

theorem has been proven.

13.5.2 Reasoning of Several Formulas

Circumcircle of Three Arbitrary Particles in Space

If a, b, c are three points in space, we now resolve their circumcenter and

circumradius. We denote their coordinates by

=(x

) , r

=(x

) , r

=(x

) .

The circumcenter of three points a, b, c is the intersection point of plane

,Π

,whereΠ

is the perpendicular plane intersecting midpoint of line

segment AB, Π

is the perpendicular plane intersecting midpoint of line seg-

ment AC,andΠ

is the plane determined by a, b, c. Hence, circumcenter o

must be on the perpendicular plane intersecting the midpoint of line seg-

ment ab, ac. The four points a, b, c, o are on same circle, so the coordinate

r =(x, y, z)ofpointo satisﬁes equations

⎧

⎪

⎨

⎪

⎩

(x − λ

)(x

− x

)+(y − λ

)(y

− y

)+(z − λ

)(z

− z

)=0,

(x − λ

)(x

− x

)+(y − λ

)(y

− y

)+(z − λ

)(z

− z

)=0,

x − x

y − y

z − z

− x

− y

− z

− x

− y

− z

=0,

(13.20)

where

+ x

,λ

+ y

,λ

+ z

,λ

+ x

+ y

,λ

+ z

To simplify,

⎧

⎪

⎨

⎪

⎩

= x(x

− x

)+y(y

− y

)+z(z

− z

) ,

= x(x

− x

)+y(y

− y

)+z(z

− z

) ,

= x(y

− z

)+y(x

− x

)+z(x

− x

) ,

(13.21)

in which

⎧

⎪

⎨

⎪

⎩



+ y

+ z

− x

− y

− z



/2 ,



+ y

+ z

− x

− y

− z



/2 ,

= x

− z

)+y

− x

)+z

− x

) .

13.5 Proof of Relative Theorems 391

Thus, the coordinate ρ

of center o

a,b,c

can be computed as follows:

)=(Δ

/Δ

,Δ

/Δ

,Δ

/Δ

) , (13.22)

in which

− x

− y

− z

− x

− y

− z

− x

− y

− z

− y

− z

− x

,Δ

− x

− z

− x

− z

− x

− y

− x

− y

− z

− x

The radius of the circle is then

a,b,c

= |oa| =

(x − x

)

+(y − y

)

+(z − z

)

. (13.23)

Let O

a,b,c

and o

a,b,c

be the circle with center o

a,b,c

,radiusρ

a,b,c

, and it lies

in the plane Π(a, b, c).

Circumscribed Sphere of Four Arbitrary Particles in Space

Four points determine a sphere. If a, b, c, d are four noncoplanar points, then

these four points determine a sphere, denoted by O(a, b, c, d). If the rectangular

coordinates of the four points a, b, c, d are (x

), where τ =1, 2, 3, 4, then

the center of the sphere determined by the four points must be an intersection

point of the perpendicular plane intersecting the midpoint of line segments

ab, ac, ad, therefore, its coordinate satisﬁes the equations

⎧

⎪

⎨

⎪

⎩

− x

)(x − λ

)+(y

− y

)(y − λ

)+(z

− z

)(z − λ

)=0,

− x

)(x − λ

)+(y

− y

)(y − λ

)+(z

− z

)(z − λ

)=0,

− x

)(x − λ

)+(y

− y

)(y − λ

)+(z

− z

)(z − λ

)=0,

(13.24)

where λ

, ··· ,λ

is given by (13.20),

+ x

,λ

+ y

,λ

+ z

If we denote the coordinates of the four points a, b, c, d by

o(a, b, c, d)=(x

) ,

then the radius of the sphere is the solution of (13.24):

r(a, b, c, d)=|ao| = |bo| = |co| = |do|



− x

)

+(y

− y

)

+(z

− z

)



1/2

392 13 Morphological Features of Protein Spatial Structure

Simplifying (13.24), we know it is equivalent to the equations

⎧

⎪

⎨

⎪

⎩

x + y

y + z

z = θ

x + y

y + z

z = θ

x + y

y + z

z = θ

in which x

4+τ

= x

1+τ

− x

, y

4+τ

= y

1+τ

− y

, z

4+τ

= z

1+τ

− z

,where

τ =1, 2, 3and

⎧

⎪

⎨

⎪

⎩



+ y

+ z

− x

− y

− z





+ y

+ z

− x

− y

− z





+ y

+ z

− x

− y

− z



The coordinates (x, y, z) of the radius of the sphere are x = Δ

/Δ

,y=

/Δ

, z = Δ

/Δ

,inwhich

,Δ

Projection of a Point on a Plane Determined

by Three Other Points

We resolve the coordinate of d



, which is the projection of point d on the plane

determined by three points a, b, c. We then denote the coordinates of d



r =(x, y, z). The following properties hold true:

1. Let r

= r

− r

, r

= r

− r

; then the normal vector n = r

× r

)ofplaneΠ(a, b, c)is



, −



=(y

− z

− x

) .

(13.25)

2. Points a, b, c, d



are coplanar, satisfying

r − r

, r

 =(x − x

+(y − y

+(z − z

=0, (13.26)

where r, r



 is the inner product of vector r and vector r



3. Let r

=(x

) be the coordinate of d,thenr − r

is parallel to the

normal vector r

.Thus,r −r

= λr

holds, where λ is an undetermined

13.5 Proof of Relative Theorems 393

coeﬃcient. We obtain the equations

⎧

⎪

⎨

⎪

⎩

x − x

= λx

= λ(y

− z

) ,

y − y

= λy

= λ(x

− x

) ,

z − z

= λz

= λ(x

− x

) .

(13.27)

From (13.25) and (13.27), we ﬁnd λ = θ

/θ

,whereθ

= r

− r

, r

,

= r

= r

, r

. So we obtain formula (13.27) to compute the coordinates

r =(x, y, z) of the projection d



Intersection Point Between the Line Through Two Points

and the Plane Through Three Points

We solve for the coordinates of the intersection point d



between the line

L = dd



(determined by two points d, d



) and the plane Π(a, b, c)(determined

by three points a, b, c). Denote the coordinates of d, d





by r =(x, y, z),



=(x



), r



=(x



), respectively, where r



is an undetermined

coeﬃcient. We have the following properties:

1. If the four points a, b, c, d



are coplanar, then we obtain (13.26), where

the undetermined variable (x, y, z) is replaced by (x



2. If three of the points d, d





are collinear, then we get r



−r = λ(r



−r),

and (x



− x, y



− y,z



− z)=λ(x



− x, y



− y,z



− z)holds.

3. By properties 1 and 2, we get

r



− r

, r

 = r



− r + r − r

, r

r



− r, r

 + r − r

, r

 =0.

Therefore, λ =

r

−r,r



r



−r,r



.Sincer, r



are known vectors, we have that r



can be determined.

Projection of a Point on a Line Determined by Two Arbitrary

Points in Space

To resolve the coordinates of the point c



, which is the projection of point c

onto the line (a, b) determined by two points a, b, we denote the coordinates

of c



by r =(x, y, z). We ﬁnd the following properties:

1. Let r

= r

− r

be the coordinate of vector

−→

ab; then, point r =(x, y, z)

satisﬁes the equations

⎧

⎪

⎨

⎪

⎩

x − x

= λx

= λ(x

− x

) ,

y − y

= λy

= λ(y

− y

) ,

z − z

= λz

= λ(z

− z

) ,

(13.28)

and

(x − x

+(y − y

+(z − z

=0. (13.29)