Shen S., Tuszynski J.A. Theory and Mathematical Methods for Bioformatics

Подождите немного. Документ загружается.

374 13 Morphological Features of Protein Spatial Structure

Deﬁnition 46. 1. Plane π is called a directed plane, if this plane divides the

space into two sides: the inside and the outside. We denote the directed

plane by π.

2. Triangle δ is called a directed triangle, if the plane π(δ) determined by

this triangle is a directed plane. We denote a directed triangle by δ.The

direction of a directed triangle δ is deﬁned by the normal line through

point o(δ), where its orientation is from outside to inside.

Directed Polyhedron

In Sect. 13.1, we have introduced the bounded, closed, connective and non-

degenerate properties of a spatial polyhedron Ω, and its representation using

a hypergraph G = {A

(3)

},whereA

contains all the vertices of the spatial

polyhedron Ω,andV

(3)

contains all the boundary triangles. We now discuss

the direction of the boundary triangle δ ∈ V

(3)

as follows.

Theorem 42. Let Ω be a spatial polyhedron, δ be one of its boundary trian-

gles, and o(δ) its circumcenter. Let  = (δ) be a line through point o = o(δ)

and perpendicular to triangle δ; then point o divides line  into two rays: 

and 

, and we have the following propositions:

1. There exists a point a on ray 

or 

such that the tetrahedron Δ(δ, a) ⊂ Ω.

2. Without loss of generality, we suppose that point a in proposition (1) is

on 

; then for any points b = o on 

, tetrahedron Δ(δ, b) must not be

in Ω.

Proposition 1 can be proved by the nondegenerate condition of the polyhe-

dron Ω, and proposition 2 can be proved by the condition that δ is a boundary

triangle. We do not detail these proofs here.

Deﬁnition 47. The spatial polyhedron Ω is a directed polyhedron, if each

boundary triangle of V

(3)

is a directed triangle, and its direction is deﬁned

as follows: The inside is the side such that the tetrahedron Δ(δ, a) ⊂ Ω

in Theorem 42, and the outside is then the other side. Here, we denote by

G = {A, V

(3)

} the directed hypergraph, where each δ ∈ V

(3)

is a directed

triangle.

If a directed polyhedron is a convex polyhedron, then we call it a convex

directed polyhedron.

Envelope and Retraction of a Directed Polyhedron

Deﬁnition 48. A directed polyhedron G



= {A



, U

(3)

} istheenvelopeofan-

other directed polyhedron G = {A, V

(3)

}, if it satisﬁes the following:

1. Both U

(3)

are sets of boundary triangles, where the triangles in them

are either completely coincident or have no common interior points of

plane. We denote the set of coincident triangles by V

(3)

13.3 Analysis of γ-Accessible Radius in Spatial Particle System 375

2. If δ ∈ V

(3)

−V

(3)

, a, b, c are three vertices of triangle δ, then there always

exists a point d ∈ A



, such that the triangle δ

= δ(a, b, d), δ

= δ(a, c, d),

= δ(b, c, d) ∈ U

(3)

. Δ = Δ(δ, d)=Δ(a, b, c, d) forms a spatial tetrahe-

dron such that triangles δ

,δ

are in U

(3)

,butnotinV

(3)

3. The directions of the triangles in U

(3)

and V

(3)

are deﬁned as follows:

(a) If δ ∈ V

(3)

, then the directions of the triangles in both {U

(3)

} and

(3)

are consistent.

(b) The direction of the four surfaces δ, δ

,δ

of tetrahedron Δ =

Δ(a, b, c, d) in condition 2 are deﬁned as follows:

i. For triangle δ, the side in which the tetrahedron Δ lies is the

inside, and the other side is the outside.

ii. For triangles δ

,δ

, the side in which tetrahedron Δ lies is the

outside, the other side is the inside.

The deﬁnitions for polyhedron G



and G are given as follows.

Deﬁnition 49. 1. If the directed polyhedron G



is the envelope of another

directed polyhedron G, then the directed polyhedron G is the retraction

of G



2. Polyhedron Δ(δ, d) is called the retracting polyhedron between directed

polyhedron G and its envelope G



.Then,δ is called the retracting tri-

angle in Δ(δ, d),andd is called the retracting point.

3. If the directed polyhedron G is the retraction of G



, then we denote the

entire retracting tetrahedrons by

Δ(G, G



)={Δ

= Δ(δ

),i=1, 2, ··· ,k} . (13.6)

It called as the retracting set of G



about G.

Deﬁnition 50. If A is a spatial particle system, G is a directed polyhedron,

and all the vertices of G are in A, then the directed polyhedron G is called the

directed polyhedron of set A.IfG, G



,andG



all are directed polyhedrons of

set A, then we have the following deﬁnitions:

1. If G



is the envelope of G, and for any retracting tetrahedron Δ(δ, d)

between G



and G, it does not contain any points in A,thenG



is called

a simple envelope of G about set A,andG is called a simple retraction

of G



about set A.

2. If G is a directed polyhedron, we denote all of its simple retractions by

, called the retracting range of G on set A.

The directed polyhedron and its envelope are shown in Fig. 13.6. Fig-

ure 13.6a shows a schematic diagram of the directed polyhedron, where the

arrow is the direction of the directed triangle. Figure 13.6b shows the relation

ﬁgure of the directed polyhedron, where graph G = {A, V } is

A = { 1, 2, ···, 15} ,V= {(1, 2), (2, 3), ··· , (14, 15), (15, 1)} .

376 13 Morphological Features of Protein Spatial Structure

Fig. 13.6a,b. A directed polyhedron and its envelope

Graph G



= {A



} is

⎧

⎪

⎨

⎪

⎩



= {1, 2, 3, 4, 6, 7, 8, 9, 11, 13, 15} ,



= {(1, 2), (2, 3), (3, 4), (4, 6), (6, 7), (7, 8), (8, 9), (9, 11),

(11, 13), (13, 15), (15, 1)} .

The direction of each tetrahedron in the envelope is shown in Fig. 13.6.

Structural Analysis of a Directed Polyhedron

Theorem 43. A directed polyhedron has the following basic properties:

1. A directed polyhedron is a convex directed polyhedron if and only if its

envelope is itself.

2. An envelope of a directed polyhedron may not be convex, but after envel-

opments, it must become a convex directed polyhedron.

Theorem 44. Let the directed tetrahedron G



, G



be the retraction of G;

their corresponding polyhedrons are Ω, Ω



,Ω



, and we denote their retracting

sets by



Δ(G



, G)={Δ



= Δ(δ



),i=1, 2, ··· ,k



} ,

Δ(G



, G)={Δ



= Δ(δ



),i=1, 2, ··· ,k



} .

(13.7)

We then identify the following properties:

1. If there are no common points between set {Δ



,i=1, 2, ···,k



} and set

{Δ



,i=1, 2, ··· ,k



}, the polyhedron is the retraction of Ω



∩ Ω



,and

it is also the retraction of Ω, then its retracting set is

Δ(G



∩G



, G)={Δ



,i=1, 2, ··· ,k



}∪{Δ



,j=1, 2, ··· ,k



} . (13.8)

2. If there are no common points between set {δ



,i=1, 2, ··· ,k



} and set

{δ



,i=1, 2, ··· ,k



}, then the polyhedron Ω



∩Ω



is the second retraction

of Ω, the ﬁrst retraction is from Ω to Ω



, and the second retraction is from



to Ω



∩ Ω



13.3 Analysis of γ-Accessible Radius in Spatial Particle System 377

We do not prove this in detail here. In general, if both Ω



and Ω



are retrac-

tions of Ω,thenΩ



∩ Ω



is still a directed polyhedron, but may not be the

retraction of Ω.

As we have mentioned above, the biological deﬁnition of the surface of

a protein is predicted on the basis of whether or not the amino acids of a pro-

tein are solvent accessible (especially by water). We now extend this deﬁnition

using mathematical language by using the γ-accessible radius to describe it.

13.3.2 Deﬁnition and Basic Properties of γ-Accessible Radius

Deﬁnition of γ-Accessible Radius

If A is a spatial particle system, Ω(A) is its convex closure and a is a point

in space, then O(a, γ) denotes a small sphere with center a and radius γ,and

O(γ) denotes a rolling sphere with radius γ.

Deﬁnition 51. For a ﬁxed spatial particle system A and any point a in Ω(A),

we say that point a is γ-accessible, if there is a broken line L which satisﬁes:

1. Point a is an endpoint of the broken line L, and the other endpoint b is

outside of the region Ω(A).

2. Denote by d a moving point on broken line L; for any d ∈ L. There are

no points of set A in the small sphere O(d, γ).

Then, we call the broken line L the γ-accessible path of the point a about A.

Deﬁnition 52. For a ﬁxed spatial particle system A and any point

a in Ω(A),

apointa has the γ-maximal accessible radius, if for all γ



<γ,pointa

is always γ



-accessible about A, and for any γ



>γ,pointa is always γ



inaccessible.

Therefore, the concept of a γ-maximal accessible radius is the maximal radius

of a small sphere which can touch other molecules in the protein. By Deﬁni-

tion 47, for a ﬁxed spatial particle system A,theγ-maximal accessible radius

of any point a in Ω(A) is uniquely determined. We denote it by γ

(a), and

call it the γ-accessible radius or the γ-function of point a (about A).

Computational Terms of γ-Accessible Radius

For a ﬁxed spatial particle system A, in order to compute the γ-function of

each point in A, we introduce the following terms, which are used frequently

in the following text:

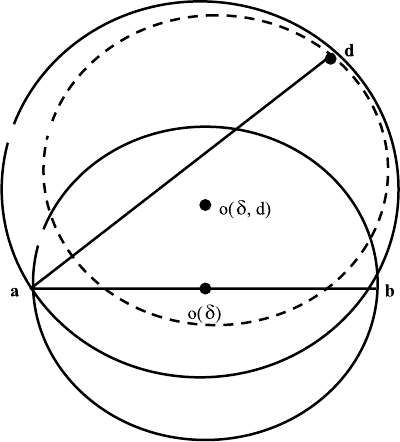
1. For a ﬁxed triangle δ or triangle δ(a, b, c), we denote the cirumcenter and

the circumradius of this triangle by o(δ),r(δ), respectively. We denoted

the circumcircle of this triangle by o(δ), and denote the plane determined

by this triangle by π(δ).

378 13 Morphological Features of Protein Spatial Structure

2. A small sphere O(r) moves freely in region Σ. This means there are no

points of set A in region Σ, and the small sphere O(r) can move in region Σ

without encountering any points of set A.

3. A small sphere O(r) can access triangle δ, this means γ[o(δ)] ≥ r,where

γ[o(δ)] is the γ-function of circumcenter o(δ) of triangle δ.Wecallγ[o(δ)]

the accessible radius of triangle δ.

4. A small sphere O(r) can traverse triangle δ, this means the small sphere

O(r) can access triangle δ,andr(δ) ≥ r,wherer(δ) is the circumra-

dius of triangle δ.Wecallmin{r(δ),γ[o(δ)]} the traversable radius of

triangle δ

5. A small sphere O(r) can access point a through triangle δ, meaning the

small sphere O(r) ﬁrst accesses triangle δ, then continues moving and

ﬁnally reaches the point a. In this moving process, we can choose an

appropriate path without encountering any points of set A. Clearly, in

later moving processes after the small sphere O(r) reaches the trian-

gle δ, it is possible that only a part of the small sphere traverses tri-

angle δ and encounters the point a, while it is also possible that the whole

small sphere has entirely traversed triangle δ and then encountered the

point a.

For computation of the γ-function of each point in the spatial particle sys-

tem A, we should choose an appropriate path for the small rolling sphere O(r)

in particle system A, such that the small sphere does not encounter any points

of set A. Then, the small sphere may traverse the triangle formed by several

points in the particle system and ﬁnally access the point a.

Basic Properties of the Calculation of γ-Accessible Radius

We formulate some basic properties of the γ-accessible radius as follows:

By the deﬁnition of the γ-accessible radius, we ﬁnd a series of basic prop-

erties, such as if we denote γ

=min{|ab|: a = b ∈ A}, then for any d ∈ A,

γ(d) ≥ γ

/2alwaysholds.

Theorem 45. a ∈ A is a zero-depth point of A if and only if for any γ>0,

point a is always γ-accessible about set A. So for any point a on a convex hull

Ω(A), γ(a)=∞ always holds.

The proof of this theorem is shown in Sect. 13.5.1.

13.3.3 Basic Principles and Methods of γ-Accessible Radius

Symbols and Terms in the Calculation of γ-Accessible Radius

As shown above, to calculate the γ-function for each point in set A,wemust

choose an appropriate path, such that a rolling sphere traverses the triangle

formed by several points in the particle system A, and ﬁnally arrives at the

13.3 Analysis of γ-Accessible Radius in Spatial Particle System 379

point a. Therefore, we need to discuss the case of an arbitrary spatial particle

system A

traversing a ﬁxed triangle δ = δ(a, b, c) and arriving at A

.Its

strict deﬁnition is presented as follows:

Deﬁnition 53. For an arbitrary ﬁxed spatial particle system A

and a ﬁxed

triangle δ = δ(a, b, c), we say that r is the accessible radius of set A

about δ,if

there exists a small rolling sphere O(r), such that in the process of traversing

triangle δ (namely, not encountering three points a, b, c) and ﬁnally arriving

at set A

(namely arriving at a point d in set A

), the small sphere does not

encounter any points in A

The maximal accessible radius of set A

about δ is called the assessible radius

of set A

about δ,inwhich,wedenotebyγ

To calculate γ

), we introduce the following symbols:

1. For a ﬁxed triangle δ = δ(a, b, c), we denote a sphere with center o(δ)and

radius r(δ)byO(δ).

2. For a ﬁxed triangle δ = δ(a, b, c)andapointd,wedenotebyO(δ, d)=

O(a, b, c, d) the circumscribed sphere determined by four points a, b, c, d,

and the corresponding center and radius are denoted by o(δ, d), r(δ, d),

respectively.

3. For a ﬁxed set A

and a triangle δ, we can construct a series of spheres:

O(δ, d) ,d∈ A

. (13.9)

Here, r(δ, d) ≥ r(δ) always holds, and the equal sign is true if and only if

point d is on the face of sphere O(δ).

4. For a ﬁxed set A

and a triangle δ,letsetA

(δ)=A

∩O(δ). If A

(δ)isnot

an empty set, then let d

be the point in set A

(δ) such that |o(δ)o(δ, d)|,

d ∈ A

(δ) is the maximum, and d



be the point such that radius of sphere

r(δ, d), d ∈ A

(δ) is the maximum. Next, we will prove d

= d



5. Let Q(δ) be a cylinder, then the underside of this cylinder o(δ)isthe

circumcircle of triangle δ and its long axis is perpendicular to plane π(δ).

Let L

be a straight line through point o(δ) and perpendicular to plane

π(δ); then q(δ) is the cylindrical face of the cylinder.

6. If Q(δ, A

)=Q(δ) ∩ A

is not an empty set, then for each d ∈ Q(δ, A

its projection on plane π(δ) is denoted by d



.Letd



be the intersection

point between line segment dd



and sphere O(δ), then calculate |dd



| (the

length of line segment dd



), and let d

be the point such that |d



| is the

minimum of |dd



|, d ∈ Q(δ, A

7. If Q(δ, A

)=Q(δ) ∩ A

is an empty set, then let d

∈ A

be the point

in A

such that the distance between d

and straight line L

is the

minimum.

Relationships among d

and the small sphere O(r), set A

are shown

in Fig. 13.7.

380 13 Morphological Features of Protein Spatial Structure

Fig. 13.7a–c. Relationship among d

and small sphere O(r), set A

Thus, the deﬁnitions of d



are given as follows:

⎧

⎪

⎨

⎪

⎩

|o(δ)o(δ, d

)| =max{|o(δ)o(δ, d)|: d ∈ A

(δ)} ,

|o(δ)d



| =max{r(δ, d): d ∈ A

(δ)} ,

|o(δ)d

| =min{|dd



|: d ∈ Q(δ, A

),d



is intersection point

of line segment dd



and sphere O(δ)} ,

|o(δ)d

| =min{|dd



|: d ∈ A



is projection of d out to line L

} ,

(13.10)

where d



is the projection of point d on plane π(δ).

Thus, we can distinguish the three cases to calculate the γ-function of

points in set A

, namely, where A

(δ) is not an empty set; where A

(δ)isan

empty set, but Q(δ, A

) is not an empty set; and where Q(δ, A

)isanempty

set.

Basic Theorem to Calculate γ-Accessible Radius

For a ﬁxed particle system A

and triangle δ,letr(δ) be the circumradius

of δ,andletγ(δ)betheγ-accessible function. The basic theorem is given as

follows.

Theorem 46. 1. If A

(δ) is not an empty set, then for d

and d



deﬁned

in (13.10), d

= d



is always true, and the γ-function of point d

)=min{r(δ),r(δ, d

)}, where the deﬁnitions of r(δ), r(δ, d

) were

given in Sect. 13.3.2.

2. If A

(δ) is an empty set and Q(δ, A

) is not an empty set, then γ

r(δ).

The proof of this theorem is given in Sect. 13.5.1.

From Fig. 13.8, we let the small sphere move upwards along the vertical

direction if Q(δ, A

) is an empty set, and then move along the horizontal

direction. In the process of moving upwards along the vertical direction, the

13.3 Analysis of γ-Accessible Radius in Spatial Particle System 381

Fig. 13.8a,b. If Q(δ, A

) is an empty set, this is an illustration of a changing ﬁgure

of the small rolling sphere

small sphere will not encounter any points in set A; thus, we can only consider

the case that the small sphere moves along the horizontal direction.

Let O



= O(o



,r(δ)) be a small sphere whose center moves upwards from

point o(δ) along the vertical direction. If the moving distance |oo



| is larger

than r(δ), this small sphere can move along the horizontal direction without

encountering any points of δ = δ(a, b, c). Let d



be the projection of point d

on plane π(δ), if h = |d



|≥r(δ), the small sphere O(r),r=min{r(δ),γ(δ)}

can move upwards along the vertical direction with distance h,andthenmove

along the horizontal direction with distance |d



|−r without encountering

any points in A. Therefore, γ(d

)=r(δ).

Similarly, for the small sphere O



= O(o



,r(δ)) which moves upwards along

the vertical direction, if |oo



| is small, then the small rolling sphere O



may

encounter three vertices a, b, c of triangle δ in the process of moving along the

horizontal direction, as shown in Fig. 13.7b, so further calculation is needed.

We build a rectangular coordinate system E,usingo(δ) as the origin. We use

line L

as the z-axis of E, with its direction pointing to the side in which

point d

lies; and we use

−→

as the Y-axis of E,whered is the projection

of d

on line L

. Then, the x-axis of E is the normal vector of the YZ-plane

which is through point o, and its direction can be determined by the right-

hand screw rule. We denote the coordinates of the four points d

,a,b,c by

=(x

),τ=0, 1, 2, 3. Here, x

= z

=0,lety

− r = ,

= h.

In a rectangular coordinate system E, if the rolling small sphere O(r)

moves upwards along z-axis a distance z, and then moves along the direc-

tion of d

adistancey, then if there exists a pair (y,z) such that the small

sphere can arrive at point d

without encountering points a, b, c, γ(d

)=r

holds.

382 13 Morphological Features of Protein Spatial Structure

To determine whether (y, z) exists or not, we denote by d



the intersection

point between line segment dd

and the cylindrical face q(δ), and denote by d



the projection of d



on plane π(δ). Thus, d



must be on the circumference of

o(δ). Without loss of generality, we suppose the radian of d



and a is closed,

and then we need only determine whether there exists a pair (y,z) such that

the small sphere arrives at point d

without encountering point a.Then(y, z)

must satisfy the following condition:

y = , z = h, x

+(y − y

)

+(z − z

)

≥ r

. (13.11)

Solving this system of equations, we have that γ(d

)=r holds if

h ≥ [r

− x

− ( −y

)

]

1/2

. (13.12)

If there does not exist a corresponding value (h, ) such that equations (13.11)

holdforaﬁxedpointd

,wereducethevalueofr to r

such that the equal

sign of (13.12) holds. Here, k,,x

are constants, hence r

exists.

In conclusion, we state the following theorem.

Theorem 47. If Q(δ, A

) is an empty set:

1. If h ≥ r,orh satisﬁes inequality (13.12), then γ(d

)=r holds.

2. If h<r,andh satisﬁes inequality (13.12), then γ(d

) ≥ r

holds, where

is the solution when (13.11) is an equality.

In proposition 2 of Theorem 47, the estimate of the lower bound of γ(d

)may

not be optimal.

Deﬁnition 54. Following from Theorems 44 and 45, we get the points d

, d

∈ A

which are the ﬁrst-meeting points of set A

after traversing triangle δ

under three cases: A

(δ) is not empty; A

(δ) is empty but Q(δ, A

) is not

empty; and Q(δ, A

) is empty. We denote by γ

)=γ

), τ =0, 1, 2 the

accessible radius of d

about triangle δ.

13.4 Recursive Algorithm of γ-Function

In the previous section, we have obtained the γ-function of each point a on

the boundary surface of Ω(A). From calculations based on Theorem 44, we

found the γ-function of some of the points of set A

. Therefore, we continue

discussing the γ function of the other points of set A

, by introducing a re-

cursive algorithm.

13.4.1 Calculation of the γ-Function Generated

by 0-Level Convex Hull

In order to calculate the γ-function of the points of set A, we ﬁrst realize that

γ(a)=∞ holds for any points in A

, by Theorem 45. We now calculate the

γ-function of the other points.

13.4 Recursive Algorithm of γ-Function 383

Fig. 13.9. Recursive calculation

We have presented the notation of V

(3)

for the representation of a 0-level

directed convex hull, where each δ ∈ V

(3)

is a directed boundary triangle of

convex closure Ω(A). We now perform the following calculations:

1. For a ﬁxed directed triangle δ = δ(a, b, c) ∈ V

(3)

,letA

= A −{a, b, c}.

For any d ∈ A

,letO(δ, d) be a sphere and let

B(δ)={d ∈ A

,O(δ, d) inside of spheroid containing no points of A

} .

(13.13)

Set B(δ) must be a nonempty set, but may not be unique; there may

be three cases for d, i.e., d ∈ A

,ord ∈ O(δ), or d is not in the

sphere O(δ).

Theorem 48. For the γ-function of the points in set B(δ), we ﬁnd the

following properties.

a) If d ∈ A

,thenγ

(d)=∞.

b) If d ∈ O(δ),thenγ

(d)=r(δ, d),wherer(δ, d) is deﬁned in Sect. 13.3.2.

We ﬁnd its properties via Theorem 46.

c) If point d is not in sphere O(δ),thenγ

(d)=r(δ),wherer(δ) is

deﬁned in Sect. 13.3.2.

Proof. We can easily prove properties 1 and 2 by Theorems 45 and 46.

The proof of property 3 is shown in Fig. 13.9.