Шелобаев С.И. Математические методы и модели

Подождите немного. Документ загружается.

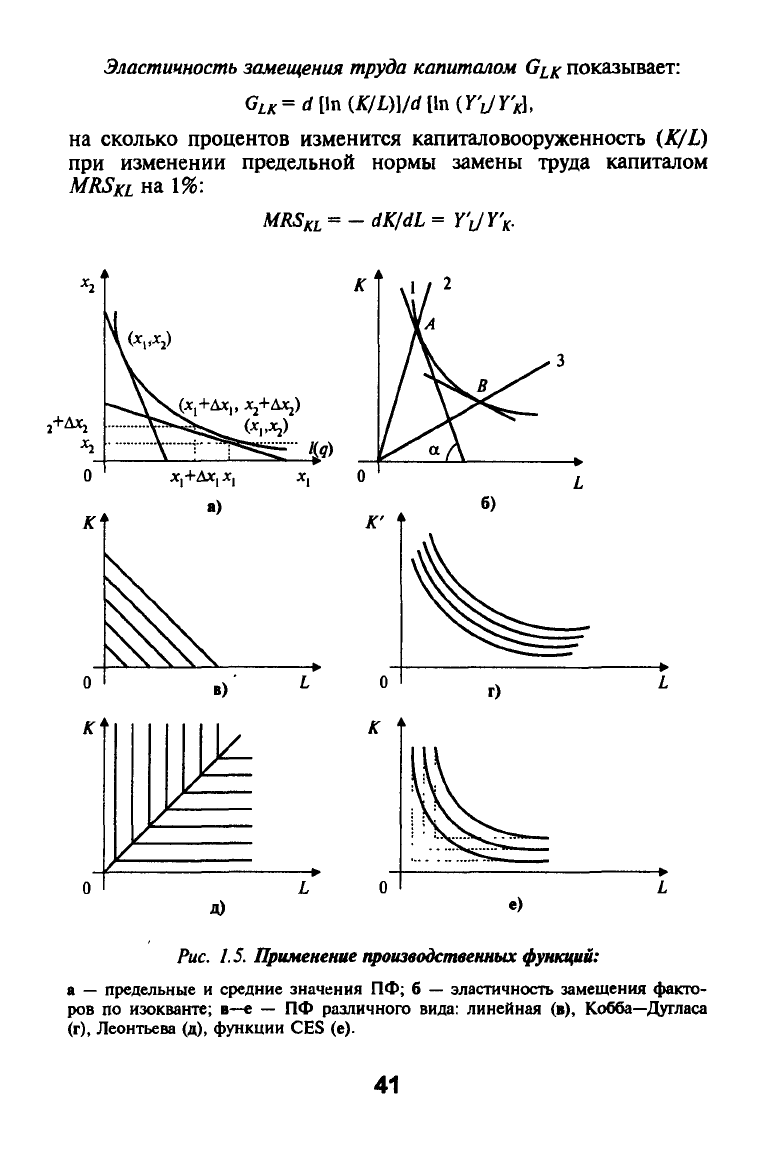
Эластичность замещения труда капиталом

GIK

показывает:

GLK=d[\n{K/L)]/dl\n{YyY'f:\,

на

сколько процентов изменится капиталовооруженность (K/L)

при

изменении предельной нормы замены труда капиталом

MRSxL

на 1%:

MRSici

= -

dK/dL =

Y'I/Y'K.

Рис. 1.5.

Применение

г^изводственных

функций:

—

предельные и средние значения ПФ; б

—

эластичность замещения факто-

ров по изокванте; в—е — ПФ различного вида: линейная (в), Кобба—Х^тласа

(г),

Леонтьева (д), функции CES (е).

Если изобразить одну из изоквант (линий уровня с Y= const)

ПФ на плоскости KL (см. рис. 1.5, б), обозначив ее цифрой 1, то

предельная норма замены в точке А —это тангенс угла наклона

этой изокванты, т. е. tga. При перемещении из точки А в точку

В по изокванте наклон касательной меняется, меняется и соот-

ношение (A/I). Это соотношение постоянно вдоль каждой пря-

мой, проходящей через начало координат (например, прямых

2 и J). Величина 1/G показывает относительное изменение тан-

генса угла наклона линии уровня в расчете на единицу измене-

ния отношения

(K/L).

Чем сильнее меняется наклон линии

уровня при переходе, скажем, из точки А в точку В (с прямой

2 на прямую S), тем больше «кривизна» линии уровня (на

рис.

1.5,

в—е

приведен

ряд

линий уровня ПФ

вица:

в —линейной Y= аК+

ЬЬ+

+ с (линейной), г —ПФКД, д

—ПФ

с бесконечной эластичностью

замещения Y = min(a^, Ы) (функция Леонтьева), е

—

производственной функции типа CES).

Линейная ПФ имеет нулевую «кривизну» и соответственно

бесконечную эластичность замещения у. ПФКД имеет эластич-

ность замещения, равную единице. Функция Леонтьева имеет

нулевую эластичность замещения: ресурсы в ней должны ис-

пользоваться в заданной пропорции и не могут замещать друг

друга. В реальной экономике степень взаимозаменяемости ре-

сурсов может быть различной, соответственно различной (а не

только нулевой, бесконечной или единичной) может быть и эла-

стичность замещения.

Рассмотрим особенности оценки производственной функции

с постоянной (но произвольной) эластичностью замещения

—

функции CES, описываемой следующей зависимостью:

Y=A

(иК-Р

+ (I - и) Ь-ру/Р,

где /> S

-1;

> О

—степень однородности; А> 0;0

и< 1.

Эластичность замещения для такой функции равна:

Еп=1/(1+р).

Если р = —

то получаем функцию с линейными изоквантами

(в частности, линейную), при р ->

в пределе получаем производ-

ственную функцию Кобба—Дугласа с G = 1, а при р ->оо

—

про-

изводственную функцию Леонтьева. Например, развитие эконо-

мики СССР описывалось следующими оценками линейно-

однородной функции CES, полученными под руковод-

ством А.Г. Гранберга за 1960—1985 гг.:

а) без учета технического прогресса

Y= 1,002(0,6412Л^'»' + O.SSSSL-os')"'/"'^';

Л2 = 0,9984; Z)»r= 1,58;

б) с учетом технического прогресса

Y= 0,966(0,4074АГЗ.оз + 0,59261-з.оз)-1/з,оз . е0.0252/.

0,9982;

DfV= 1,76.

С точки зрения статистик R^ и DJV обе зависимости получи-

лись значимыми при разных оценках показателя эластичности

замещения G (G = 1/(1 + р). В целом оценка эластичности за-

мещения зависела от конкретной специфики и составляла около

0,4, что говорит о невысокой степени взаимозаменяемости труда

и капитала (в функции Кобба—Дугласа предполагается, что эла-

стичность замещения у априори составляет единицу). Ошибоч-

ность исходной гипотезы о степени взаимозаменяемости факто-

ров может служить причиной недостаточной статистической

значимости оценок производственной функции Кобба—Дугласа.

Более подробно разновидности данного класса моделей рас-

смотрены в [1,2,78] и др.

Далее исследуем экономико-математические методы, отно-

сящиеся к оптимальным методам принятия решений на основе

моделей математического программирования.

Глава

Математические модели оптимизации

ресурсов

принятия решений

Для рещения самых разнообразных задач оптимизации необхо-

димо иметь соответствующую математическую модель.

боль-

шинстве ситуаций самые различные

по

содержанию задачи ока-

зываются частными случаями одной задачи оптимизации.

2.1.

Общий случай математической постановки задачи

оптимизации

Если

не

рассматривать детально составление математической

модели

на

конкретных примерах,

как это

делается

большинст-

ве посвященных этой проблеме работ, например

[16, 54, 82,

125—130],

Перейти

общему случаю,

то

задача оптимизации

общем случае, включающая

три

компоненты (целевую функцию

ограничения

gf и

граничные условия), имеет следующую

ма-

тематическую постановку:

f(Xi,X2, ...,х„)

max(min);

g,{x^,X2,....x„){^,

= ,^}d,•

g,(x„X2,...,x„){i,

= ,^}d,;

(2.1)

f„(x,.JC2,...,x„)i(^=,^}^«;

fly

iXj

<.bj;i

\,m;j

\,n,

где

fly

bj —нижнее

и верхнее предельно допустимые значения

Xj.

Задачу

(2.1)

можно представить

в еще

более общей компакт-

ной форме записи:

- f(Xj) -^

max(min);

gi{Xj){i.

= ,^)d,; \ (2.2)

iXj й

bj-,

i = l,m;j = 1,л

Граничные условия

показывают предельно допустимые значе-

ния искомых переменных, и в общем случае они могут бьггь

двусторонними типа aj < xj

bj. Вместе с тем на практике дос-

таточно часто возникают следующие частные случаи:

1) в технических, экономических и других видах расчетов иско-

мые величины обычно являются положительными или равными

нулю.

этом случае в задаче (2.2) принимается

оу

О,

Лу

= « и на-

кладывается только требование неотрицательности Xj>0;

2) в ряде случаев значение величины xj может задаваться. Ес-

ли принять, что должно выполняться требование

= х?, где х/

—

заданное значение, то граничные условия в задаче (2.2) мож-

но записать следующим образом:

Ограничения

обычно выражают определенные зависимости

между переменными величинами, которые по своей сути могут

быть теоретическими (формульными) и статистическими. Тео-

ретические

зависимости обычно справедливы при любых усло-

виях и для их получения не требуется никаких дополнительных

измерений. Однако на практике достаточно часто между пара-

метрами модели нет известной функциональной зависимости.

Так, например, если мы желаем оптимизировать использование

общественного транспорта города в течение суток, то нам необ-

ходимо знать, как пассажиропоток распределен во времени. Ес-

тественно, что такой готовой зависимости нет, и для ее получе-

ния потребуется осуществить сбор и обработку статистических

данных, чтобы получить определенную аналитическую зависи-

мость, которая и будет тем офаничением, которое следует

включить в задачу оптимизации.

Значения переменных, удовлетворяющие заданным фанич-

ным условиям и офаничениям, называют

допустимым

решением

задачи. Иногда случается, что в задачу включаются противоре-

чивые по смыслу требования, выполнить которые невозможно.

Такая ситуация приводит к

несовместным

задачам, которые в

планировании называют

несбалансированными планами

(когда нет

и не может быть допустимых решений). Обычно же, если задача

составлена правильно, то в общем случае она имеет набор до-

пустимых решений. Чтобы из данного набора допустимых ре-

шений лицо, принимающее решение (ЛПР), могло выбрать одно

наилучшее, необходимо договориться, как и по какому признаку

его найти.

дальнейшем не будет речи о правильных решениях,

потому что мы просто не знаем, что это такое. Мы будем

говорить только об оптимальных решениях (от лат. optimus —

наилучший). Заметим, что наилучшего решения во всех смыслах

быть не может, оно может быть наилучшим (оптимальным)

только в одном, строго установленном смысле. ЛПР должно аб-

солютно точно представлять, в чем заключается оптимальность

принимаемого решения, т. е. по какому критерию (от ф.

kriterion — мерило, оценка, средство для суждения) принимае-

мое решение должно быть оптимально.

Критерий часто называют целевой функцией, функцией це-

ли,

а в математических работах

—

функционалом. Критерий в

общем случае может оценивать качественные свойства объекта,

причем как желательные пдя субъекта (обычно с максимальным

уровнем или значением, например, прибыль, производитель-

ность, надежность), так и нежелательные для него (или мини-

мальные — непроизводительные затраты, расход материала,

простои оборудования и др.). Если при принятии решения тре-

буется максимизировать какое-то свойство (к примеру, прибыль,

производительность или надежность), то в результате решения

задачи критерий будет иметь наибольшее значение из всех до-

пустимых решений. Если же требуется минимизировать крите-

рий (стоимость, расход материала, время простоев оборудова-

ния),

то в результате решения критерий будет иметь наимень-

шее значение из всех допустимых.

Множество различных по смыслу задач оптимизации, окру-

жающих нас, например, из табл. 2.1, нельзя эффективно решить

без привлечения ЭВМ, без знаний экономико-математических

моделей, практических навыков составления математических

моделей решения задач и применения их в среде существующего

профаммного обеспечения.

Таблица

2.1.

Классификация задан оптияшзаищ /фщессов

и приняптя решений

Область

применения

Производство

Образование

Культура

Бизнес

Экономика

Финансы

Управление

Различные задачи

распределения ре-

сурсов (матери-

альных, финансо-

вых, информацион-

ных, трудовых)

Проектирование

Оптимизация

параметров объек-

та проектирования

Оптимизация

структуры объекта

проектирования

Разработка

техно-

логических

процес-

сов

Оптимизация

маршрута изготов-

ления изделия

Отимизация па-

раметре» технологи-

ческих процессов

Продолжение

табл.

2.1

Искусство

Бытовая сфера

Принятие реше-

ний

2 3

Оптимизация

функционирова-

ния

Выбор режима

работы, обеспече-

ния качества и

эффективности

Основные задачи управления деятельностью человека можно

отнести к классу задач распределения и оптимизации ресурсов.

Любой объект в процессе управления, проектирования или экс-

плуатации характеризуется своим устройством и действием,

причем устройство определяется его структурой и параметрами,

а действие — процессом функционирования. Например, техно-

логический процесс можно определить как последовательность

работ, которые обусловливают превращение сырья в готовую

продукцию; такую последовательность работ называют

маршру-

том;

каждую операцию, входящую в марщрут, можно охаракте-

ризовать определенными режимами обработки, управления,

контроля, функционирования. Заметим, что и процессы функ-

ционирования объекта проектирования, и технологические про-

цессы характеризуются изменением некоторых параметров во

времени, которые подразделяются на непрерывные и дискрет-

ные (непрерывные процессы протекают в металлургии, энерге-

тике,

химии и др., а дискретные — в машиностроении, эконо-

мике, образовании и т. п.).

В любых математических моделях можно вьщелить следую-

щие элементы (рис. 2.1): исходные данные, зависимости, описы-

вающие целевую функцию, и офаничения.

Исходные данные

Детерминированные

Случайные

Искомые переменные

Непрерывные

Дискретные

Зависимости

Линейные

Нелинейные

Рис. 2.1. Разновидности элементов математической модели

Зависимости между переменными, как целевые функции, так

и ограничения, могут быть линейными и нелинейными. Напом-

ним, что

линейными

называют такие зависимости, в которые пе-

ременные входят в первой степени и нет их произведения; если

переменные входят не в первой степени или есть произведение

переменных, то зависимости являются

нелинейными.

Сочетание

разнообразных элементов модели приводит к различным клас-

сам задач оптимизации, требуюшим разных методов решения и

разных программных средств (табл. 2.2).

Для экономических систем наиболее характерны задачи оп-

тимизации и распределения ресурсов, решаемые методом ли-

нейного профаммирования, для которого разработаны надеж-

ные алгоритмы, реализованные в поставляемом с ЭВМ про-

фаммном обеспечении; более сложные задачи (целочисленные,

нелинейные) оптимизации можно свести к задачам линейного

профаммирования. Большинство задач оптимизации, присущих

техническим системам, как правило, относится к задачам нели-

нейного профаммирования. В целом методы математического

профаммирования являются частью науки, традиционно назы-

ваемой

исследованием

операций.

Таблица

2.2.

Раауюстраиенные задачи математического

программирования

Исходные данные

Детерминированные

или постоянные

Случайные

Переменные

Непрерывные

Целочисленные

Непрерывные,

целочисленные

Непрерывные

Завиашости

Линейные

Нелинейные

Линейные

Задачи оптимизации

Линейного программирова-

ния (ЛП)

Целочисленного профам-

мирования (ЦЧП)

Нелинейного программиро-

вания (НЛП)

Стохастического програм-

мирования (СТП)

Рассмотрим общие постановки задач и способы решения

наиболее распространенных задач оптимизации.

2.2.

Методы оптимизации и распределения ресурсов

на основе задачи линейного программирования

Подобные методы широко применимы в производстве,

транспорте, организации процессов, в об^'чении, руководстве

персоналом и др. К числу наиболее известных задач, решаемых

этим методом, относятся задача о назначениях, транспортная

задача и др. [78, 82, 128—130].

Задача о назначениях и распределении работ является част-

ным случаем транспортной задачи, в которой приняты следую-

щие допущения: число поставщиков т равно числу потребите-

лей л; запасы каждого поставщика о, = 1; заявки каждого потре-

бителя bj= 1; каждый поставщик может поставлять фузы только

одному потребителю; каждый потребитель может получать фузы

только от одного поставщика.

Если не учитывать направление оптимизации целевой функ-

ции (шах или min), что не влияет на аналитические зависимо-

сти,

то модель транспортной задачи при принятых выше допу-

щениях получает вид модели задачи о назначениях. Если сумма

всех запасов А у поставщика равняется сумме всех заявок

В потребителей, то такую транспортную задачу называют

сбалан-

сированной;

если А

В,

то

задача является

несбалансированной,

ее математическая модель может иметь вид:

т л

Е 'ZcyХу->т\п

Y,xij<ai;

\,т;

(VI

Y.xi/tbj;

1,л;

хо >

Знак неравенства в офаничениях для запасов а, означает,

что объем фуза, вывозимый от любого /-го поставщика по за-

явкам всех потребителей, не может превышать имеющегося у

него запаса, при этом часть запаса фуза может остаться невы-

везенной. Аналогично знак неравенства в Офаничениях для

заявок bj означает, что фуз, получаемый ./-м поставщиком,

должен быть не меньше заявки, но превышение заявки при

этом допускается.

Модель сбалансированной задачи является частным случаем

модели несбалансированной задачи. Несбалансированная модель

транспортной задачи является достаточно универсальной моде-

лью,

описывающей множество задач распределения однородных

ресурсов

—

работ, назначений, материальных и трудовых ресур-

сов,

транспортировки фузов, распределения инвестиций, фи-

нансовых средств и др., которые можно успешно решить, если

знать ответы на вопросы:

• В каком смысле распределение средств должно быть наи-

лучшим?

• Какой вклад дает каждый объект (субъект) в целевую

функцию?

Любая правильно составленная задача планирования имеет

бесчисленное множество допустимых решений. Какое же из них

выбрать? Мы уже знаем, чтобы ответить на этот вопрос, необхо-

димо прежде всего сформулировать задачу оптимизации, при

решении которой возможна лишь одна из двух взаимоисклю-

чаемых постановок: либо при заданных ресурсах максимизиро-

вать получаемый результат, либо при заданном результате ми-

нимизировать используемые ресурсы.

Если через Q обозначить ресурсы, через R —результат их при-

менения, то при заданных зависимостях результата и потребных

ресурсов от количества выпускаемой продукции R

=f(,xj);

Q =fixj)

две постановки задачи распределения ресурсов можно записать

следующим образом:

для первой постановки

== Л

->тах; Q <

Q,;

(2.3а)

для второй постановки

F2=Q^mm; R>R,. (2.36)

Значит, поставить ее можно в одном из двух следующих ва-

риантов: либо максимизирювать выпуск продукции с заданного

оборудования, либо минимизировать количество оборудования,

используемого при вьшуске заданного объема продукции.

В общем случае математическая модель задачи распределе-

ния ресурсов с числом переменных я и офаничений т имеет

следующий вид:

'^cjXj-* max (min);

2_,

Oj/

•

xj ^ bi;

djiXj.uDj; i

l,m; j

\,n,

(2.4)

где

— коэффициенты в целевой функции; а^ — норма расхода /-го

ресурса для выпуска единицы у-й продукции; 6, —имеющийся ресурс; dj

— минимальное и максимальное допустимые значения

Xj.