Sha W., Malinov S. Titanium Alloys: Modelling of Microstructure, Properties and Applications

Подождите немного. Документ загружается.

Titanium alloys: modelling of microstructure258

The novel approach of combining CA with theoretical principles of DRX

links meso- and micro- structural features with continuum flow properties of

metallic materials and with processing conditions. The influences of hot

deformation parameters, e.g. strain, strain rate and deformation temperature,

on the characteristics of DRX, e.g. the microstructural evolution and the

flow stress–strain behaviour, are analysed in this chapter.

10.2 Microstructural evolution of Ti-6Al-4V during

thermomechanical processing

10.2.1 Flow stress–strain curves

The flow stress is almost constant under all conditions, as shown in typical

curves of the hot-pressed specimens in Fig. 10.1. The stress–strain

characteristics may be attributed to the microstructural changes due to phase

True stress

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7

True strain

(a)

0.5

1.0

0.1

0.05

True stress

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7

True strain

(b)

0.5

1.0

0.1

0.05

10.1

Stress–strain curves for different hot working temperatures and

strain rates. (a) 1000 °C; and (b) 1050 °C. The vertical axis scale is

obscured due to proprietary data.



Cellular automata method for microstructural evolution 259

transformation, adiabatic heating and evolution of dynamic recovery or dynamic

recrystallisation during hot processing. Further evidence for these is provided

in later sections.

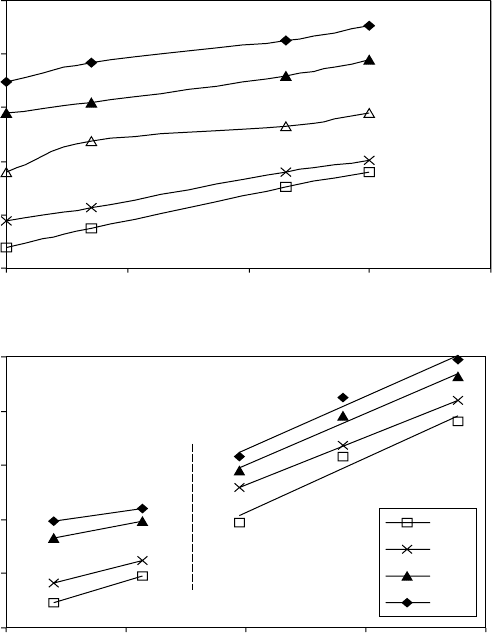
The experimental stress–strain curves show that the flow stress increases

with strain rate at a given temperature and decreases with increasing temperature

at a given strain rate (Fig. 10.2). Significant flow softening occurs for hot-

pressing at the lower temperatures. There are two possible mechanisms

responsible for the flow softening: (i) adiabatic heating during hot-pressing;

and (ii) α to β phase transformation during hot-pressing.

ln (σ, MPa)

5.5

5.0

4.5

4.0

3.5

3.0

–3 –2 –1 0 1

log (

–1

)

(a)

850 °C

900 °C

950 °C

1000 °C

1050 °C

ln (σ, MPa)

2.3

2.1

1.9

1.7

1.5

1.3

β regime

α + β regime

Strain rate

0.05

0.1

0.5

7.4 7.8 8.2 8.6 9.0

(1/

) × 10

–1

)

(b)

10.2

Variation of flow stress of Ti-6Al-4V with (a) strain rate at

different processing temperatures and (b) temperature at different

strain rates.



Titanium alloys: modelling of microstructure260

10.2.2 Phase transformation

Phase transformation during thermomechanical processing is an important

feature for α + β titanium alloys. The microstructure of the non-deformed

samples shows that all the prior-α lamellar phase has transformed into equiaxed

grains prior to hot working. After quenching from the β-processing

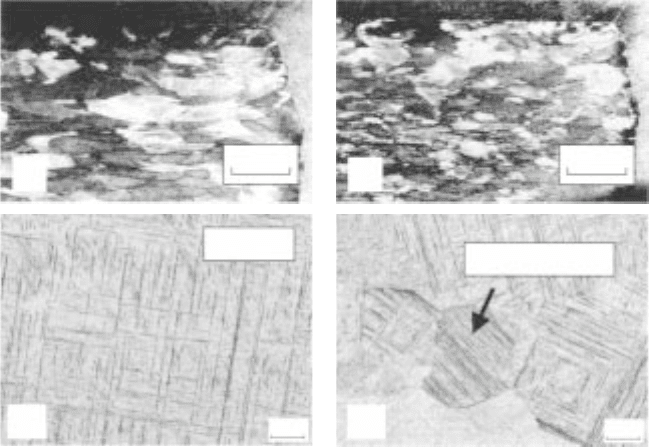
temperatures, the β-grains transformed into martensite. The features are shown

in Fig. 10.3 where two samples were processed at

= 0.1 s

–1

The experimental results show that the behaviour of deformation and

transformation of the prior-α lamellar phase is very complex at the processing

temperatures. Phase transformation of the prior α lamellar phase may be

distinguished by three stages: non-transformed, partially-transformed and

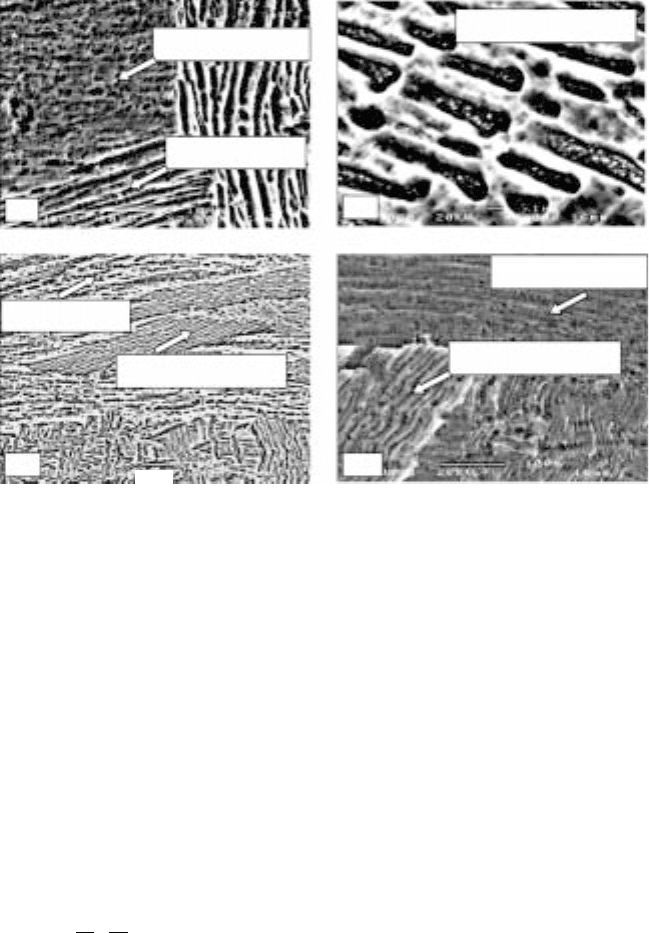
completely transformed, respectively. The final microstructural morphology

of the samples deformed in the α + β phase field is characterised by at least

five different types (Fig. 10.4). These are: (i) non-distorted prior-α platelets

with an interplatelet β phase (prior-α microstructure before hot deformation);

(ii) distorted prior-α platelets with an interplatelet β phase; (iii) spheroidised

prior-α lamella zone; (iv) diffused prior-α phase zone; and (v) transformed-

β phase zone, respectively. The morphology depends on the local

thermomechanical history corresponding to different stages of transformation

(Ding et al., 2002).

(a)

(b)

3 mm 3 mm

50 µm

Martensite

Recrystallised grain

10.3

Micrographs of two hot-pressed samples for the strain rate of

0.1 s

–1

. The conditions are: (a, c) 1000 °C; and (b, d) 1050 °C.



Cellular automata method for microstructural evolution 261

10.2.3 Dynamic recrystallisation

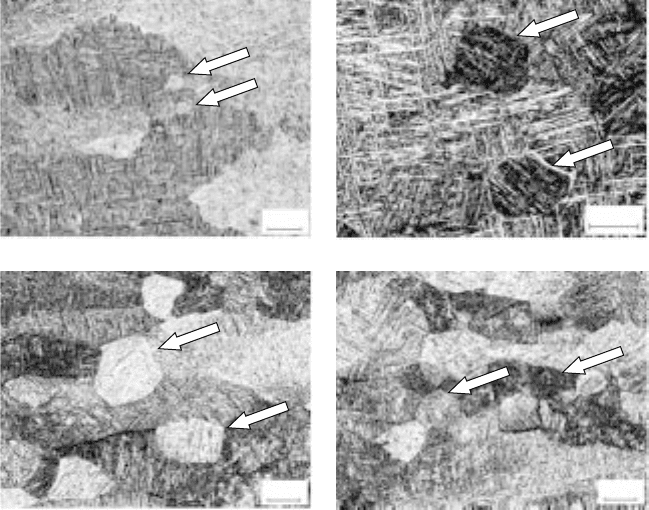
Microstructural observations confirm that dynamic recrystallisation occurs

during hot working of the Ti-6Al-4V alloy in the β phase field at the

temperatures of 1000 and 1050 °C. Figure 10.5 presents representative

micrographs that exhibit various levels of dynamic recrystallisation. The

extent is relatively small at 1000 °C. The percentage increases with temperature.

When the processing is at 1050 °C, relatively high levels of dynamic or

metadynamic recrystallisation are evident for strain rates of 0.5 and 1 s

–1

According to literature, the mean size of dynamically recrystallised (DRXed)

grains increases monotonically with decreasing stress. It remains constant

during hot deformation, and can be calculated according to the following

equation:









[10.1]

where σ is the flow stress, µ is the shear modulus, b is Burger’s vector, D is

the mean stable size of the DRXed grains, the exponent n is 2/3, and K is a

constant in the range of 1–10. Taking K = 10 and b = 0.286 nm, the calculated

mean sizes of the stable dynamic recrystallised grains are around 53 and

(a)

(b)

Diffused prior-α (iv)

Non-distorted (i)

Transformed-β (v)

Distorted prior-α (ii)

Diffused prior-α (iv)

Spheroidised prior-α (iii)

10.4

Five different morphologies of α phase after hot working in the

α + β field (850 °C, 0.5 s

–1

) after post-deformation quenching.

10µm



Titanium alloys: modelling of microstructure262

42 µm, respectively, at the temperature of 1050 °C and the strain rates of 0.5

and 1 s

–1

. The measured mean sizes of the DRXed grains in Fig. 10.5c and

d are 336 and 320 µm, respectively, which are much greater than the calculated

values. The reason for the discrepancy may be attributed to meta-dynamic

recrystallisation or rapid grain growth occurring immediately after the hot

deformation at the relatively high processing temperature.

10.3 The simulation model

The CA method is an algorithm describing the discrete spatial and/or time

evolution in a physical system by applying a deterministic or probabilistic

transformation rule. The space of interest is divided into finite cells, and the

state of every cell is determined by the states of its neighbouring sites according

to a given transformation rule. Here, the CA method is used to simulate the

equiaxed growth of the DRXed grains, and the theoretical model of DRX is

used to calculate its characteristics, e.g. the critical nucleation condition and

100 µm

(a)

30 µm

(b)

200 µm

(d)

200 µm

(c)

10.5

Micrographs showing dynamic recrystallisation. The conditions

are: (a) 1000 °C and 0.05 s

–1

; (b) dark field photo of (a) at higher

magnification; (c) 1050 °C and 0.5 s

–1

; and (d) 1050 °C and 1 s

–1

Arrows point to recrystallised prior-β grains.



Cellular automata method for microstructural evolution 263

the nucleation rate, the dislocation density variation in the primary grains,

and the growth kinetics of the DRXed grains (R-grains), which are all closely

associated with the practical hot working parameters.

A continuous nucleation model is used to simulate the DRX. It is assumed

that a constant nucleation rate exists during the entire thermomechanical

processing if DRX occurs. The nucleation rate for DRX is assumed to be a

function of both the temperature and the strain rate:

˙˙

( –

, ) = exp

act

εε









[10.2]

where C is constant,

is the strain rate, T is the deformation temperature,

act

is the activation energy, R is the gas constant, and the exponent m is

constant. The constant C can be obtained according to experimental results.

The driving force for the nucleation of DRX and the growth of the nuclei

originates from the strain energy induced by dislocations during thermo-

mechanical processing. Variation of the dislocation density during hot working

is dependent on two competing processes: work hardening and dynamic

recovery (softening). There is a phenomenological approach (KM model) to

predict the variation of dislocation density with strain for Stage III hardening

of metals. The model is based on the assumption that the kinetics of plastic

flow are determined by a single structural parameter, the dislocation density

ρ. The dislocation density variation can be expressed as:

= –

ρkk

[10.3]

where ε is true strain, k

is a constant, and k

is the softening parameter

which is a function of temperature and strain rate, k

= k

(

, T). The strain-

dependent dislocation component of the flow stress, due to the dislocation–

dislocation interaction, can be expressed as:

σαε µ

= ( , )

[10.4]

where α(

, T) is a dislocation interaction term that approaches 0.5 as

T → 0.

For a deforming matrix, the variation of its dislocation density can be

calculated using Eq. [10.3] from the beginning of deformation. When its

value exceeds the critical dislocation density for the nucleation of DRX,

DRXed nuclei appear on the grain boundaries. For the newly formed grain,

the initial dislocation density is set to be zero inside the DRXed grain, but

increases when the grain grows with continuous deformation. When the

dislocation density of the DRXed grain reaches the density of the matrix, the

driving force for its growth becomes zero, and the grain ceases to grow.

The driving force for growth of the DRXed grains comes from the stored



Titanium alloys: modelling of microstructure264

strain energy difference between the DRXed grains and the matrix. The

growth velocity V is proportional to the driving force F, where V = MF and

M is the grain boundary mobility. If the DRXed grain is assumed to be

spherical, the driving force F can be expressed as:

Fr r = 4 ( – ) – 8

πτρ ρ πγ

[10.5]

where ρ

and ρ

are dislocation densities of the matrix and the DRXed grain,

respectively, r

is the radius of the DRXed grain, τ is the dislocation line

energy, γ is the grain boundary energy, which can be calculated from the

Read-Shockley equation:

γγ =

1 – ln⋅









[10.6]

where

is the grain boundary misorientation, γ

and

are the boundary

energy and misorientation when the grain boundary becomes a high angle

boundary (taken as 15°), respectively.

10.4 Simulated microstructural evolution during

dynamic recrystallisation

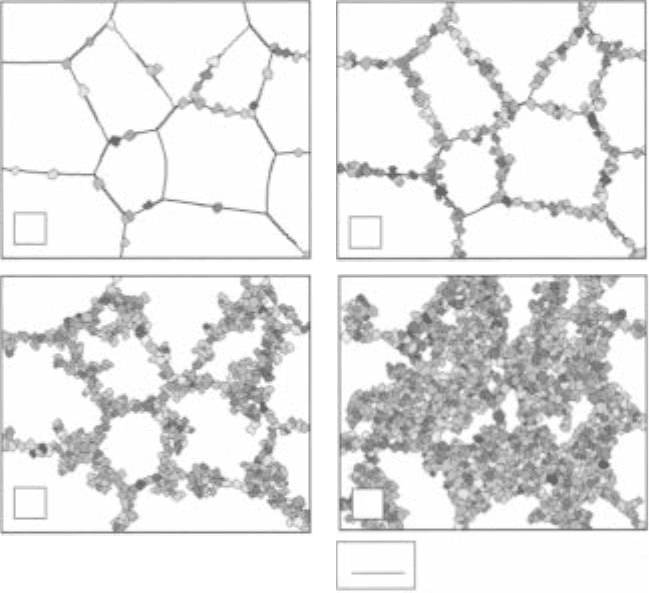
Figure 10.6 shows the simulated microstructure for the alloy hot-pressed

under specific deformation conditions (

= 1 s

–1

, T = 1050 °C). In order to

simulate the experimental observations, the initial mean diameter of the

prior grains in the calculation is controlled to be around 1.06 mm, close to

the actual prior grain size of 1.1 mm. The simulated percentage of DRX at

a strain of 0.7 is 3.2%, which agrees well with the actual percentage of DRX,

3.1%, under the experimental conditions. From Fig. 10.6d, a large strain of

45 is needed for the percentage of DRX to reach 65.6%.

In the following, we investigate the influences of temperature and strain

rate on DRX, using simulation carried out under various deformation conditions.

The DRXed grain size decreases with increasing strain rate (Fig. 10.7). The

mean size of the DRXed grains is 62 µm at the strain rate of 0.3 s

–1

, but

decreases to 30 µm at the strain rate of 3 s

–1

. The percentage of DRX

decreases from 34.5% to 15.2% when the strain rate varies from 0.3 to

3 s

–1

. The percentage of DRX increases with increasing deformation

temperature, and the mean size of the DRXed grains increases from 37 µm

at 1000 °C to 49 µm at 1100 °C (Fig. 10.8).

The experimental and simulated microstructures of the Ti-6Al-4V after

hot-pressing in the β phase field are compared in Fig. 10.9, (Ding and Guo,

2002).



Cellular automata method for microstructural evolution 265

10.5 Simulated flow stress–strain behaviour

The calculated stress evolution curves are very close to the experimental

results (Fig. 10.10). The flow stress fluctuates at low strain rates in the small

strain range. When the strain rate is higher than 0.1 s

–1

, the stress reaches the

steady-state regime very rapidly at a small strain (< 0.01).

The phenomenon of flow stress oscillation is frequently observed during

DRX. The flow stress depends not only on the rate of dislocation accumulation

in the R-grains, which is influenced by the thermomechanical processing

parameters (strain rate and temperature), but also on the grain size.

The dislocation density fluctuates at small strain rates and small strains

(Fig. 10.11). When the strain rate reaches 0.5 s

–1

, the dislocation density

rapidly achieves a stable value. The dislocation density exhibits pronounced

(c)

(d)

300 µm

(a)

(b)

10.6

Simulated microstructure of the Ti-6Al-4V alloy during

thermomechanical processing in the β phase field at 1050 °C and a

strain rate of 1 s

–1

. The strains are: (a) 0.7 (mean size of the DRXed

grains 42.8 µm); (b) 5 (43.6 µm); (c) 15 (43.2 µm); and (d) 45 (43.5

µm).



Titanium alloys: modelling of microstructure266

fluctuations at relatively high temperatures, and reaches stable values rapidly

when the temperature is only 1000 °C.

10.6 Summary of the simulation method and its

capabilities

Dynamic recrystallisation and/or rapid grain growth occurs after hot

deformation. Both the percentage of DRX and the mean size of the DRXed

(a)

(b)

300 µm

(a)

300 µm

(b)

10.7

Simulated microstructure of the Ti-6Al-4V alloy during

thermomechanical processing in the β phase field at 1050 °C and a

true strain of 10. The strain rates are: (a) 0.3 s

–1

; and (b) 3 s

–1

. True

strain is ln(original length/final length)

10.8

Simulated microstructure of the Ti-6Al-4V alloy during

thermomechanical processing in the β phase field at different

temperatures for a given strain rate of 1 s

–1

and a true strain of 6.

The deformation temperatures are: (a) 1000 °C; and (b) 1100 °C.



Cellular automata method for microstructural evolution 267

grains increase with increasing temperature and decreasing strain rate. The

mean dislocation density fluctuates at lower strain rates, and gradually stabilises

with increasing strain rate. Conversely, it fluctuates more severely at a higher

temperature and reaches a stable state with reduced fluctuation at a lower

temperature.

The cellular automaton approach described in this chapter provides an

essential link for future multiscale modelling to bridge mesoscopic dislocation

activities to microscopic grain boundary dynamics, allowing accurate

(b)

3 mm

(a)

10.9

Microstructure of the Ti-6Al-4V alloy after hot pressing at

1050 °C with a strain rate of 0.5 s

–1

and strain of 0.7: (a)

experimental; and (b) simulated.

Flow stress

0 0.01 0.02 0.03 0.04 0.05 0.06

Strain

T: 1000 °C

3.0

1.0

0.5

0.1

0.05

10.10

Calculated variation of flow stress with strain at a deformation

temperature of 1000 °C and different strain rates (0.05–3 s

–1

). The

vertical axis scale is obscured due to proprietary data.

