Schutz B. A first course in general relativity
Подождите немного. Документ загружается.

343 12.2 Cosmological kinematics: observing the expanding universe
t
The trace of this tensor is also a scalar, and must also therefore be constant. So instead
of computing the Ricci scalar curvature, we simply require that the trace G of the three-
dimensional Einstein tensor be a constant. (In fact, this trace is just −1/2 of the Ricci
scalar.) The trace is
G = G
ij
g
ij
=−
1
r
2
e
2
(1 − e
−2
)e
−2
− 2r e
−2
r
−2
=−
1
r
2
+
1
r
2
e
−2
(1 − 2r
)
=−
1
r
2
[1 − (r e
−2
)
]. (12.9)
Demanding homogeneity means setting G to some constant κ:
κ =−
1
r
2
[r(1 −e
−2
)]
. (12.10)
This is easily integrated to give
g
rr
= e
2
=
1
1 +
1
3
κr
2
− A/r
, (12.11)
where A is a constant of integration. As in the case of spherical stars, we must demand local
flatness at r = 0 (compare with § 10.5): g
rr
(r = 0) = 1. This implies A = 0. Defining the
more conventional curvature constant k =−κ/3gives
g
rr
=
1
1 − kr
2
dl
2
=
dr
2
1 − kr
2
+ r
2
d
2
. (12.12)
We have not yet proved that this space is isotropic about every point; all we have shown
is that Eq. (12.12) is the unique space which satisfies the necessary condition that this
curvature scalar be homogeneous. Thus, if a space that is isotropic and homogeneous exists
at all, it must have the metric, Eq. (12.12), for at least some k.
In fact, the converse is true: the metric of Eq. (12.12) is homogeneous and isotropic
for any value of k. We will demonstrate this explicitly for positive, negative, and zero k
separately in the next paragraph. General proofs not depending on the sign of k can be
found in, for example, Weinberg (1972) or Schutz (1980b). Assuming this result for the
time being, therefore, we conclude that the full cosmological spacetime has the metric
ds
2
=−dt
2
+ R
2
(t)
$
dr
2
1 − kr
2
+ r
2
d
2
!
. (12.13)
This is called the Robertson–Walker metric. Notice that we can, without loss of generality,
scale the coordinate r in such a way as to make k take one of the three values +1, 0, −1. To

344 Cosmology
t
see this, consider for definiteness k =−3. Then re-define ˜r =
√
3r and
˜
R = 1/
√
3R, and
the line element becomes
ds
2
=−dt
2
+
˜
R
2
(t)
$
d˜r
2
1 −˜r
2
+˜r
2
d
2
!
. (12.14)
What we cannot do with this rescaling is change the sign of k. Therefore there are only
three spatial hypersurfaces we need consider: k = (−1, 0, 1).
Three types of universe
Here we prove that all three kinds of hypersurfaces represent homogenous and isotropic
metrics that have different large-scale geometries. Consider first k = 0. Then, at any
moment t
0
, the line element of the hypersurface (setting dt = 0) is
dl
2
= R
2
(t
0
)
dr
2
+ r
2
d
2
= d(r
)
2
+ (r
)
2
d, (12.15)
with r
= R(t
0
)r. (Remember that R(t
0
) is constant on the hypersurface.) This is clearly
the metric of flat Euclidean space. This is the flat Robertson–Walker universe. That it is
homogeneous and isotropic is obvious.
Consider, next, k =+1. Let us define a new coordinate χ(r) such that
dχ
2
=
dr
2
1 − r
2
(12.16)
and χ = 0 where r = 0. This integrates to
r = sin χ , (12.17)
so that the line element for the space t = t
0
is
dl
2
= R
2
(t
0
)[dχ
2
+ sin
2
χ (dθ
2
+ sin
2
θ dφ
2
)]. (12.18)
We showed in Exer. 33, § 6.9, that this is the metric of a three-sphere of radius R(t
0
), i.e. of
the set of points in four-dimensional Euclidean space that are all at a distance R(t
0
)from
the origin. This model is called the closed,orspherical Robertson–Walker metric and the
balloon analogy of cosmological expansion (Fig. 12.1) is particularly appropriate for it. It is
clearly homogeneous and isotropic: no matter where we stand on the three-sphere, it looks
the same in all directions. Remember that the fourth spatial dimension – the radial direction
to the center of the three-sphere – has no physical meaning to us: all our measurements are
confined to our three-space so we can have no physical knowledge about the properties or
even the existence of that dimension. At this point we should perhaps think of it as simply
a tool for making it easy to visualize the three-sphere, not as an extra real dimension,
although see the final paragraph of this chapter for a potentially different point of view
on this.
The final possibility is k =−1. An analogous coordinate transformation (Exer. 8, § 12.6)
gives the line element
dl
2
= R
2
(t
0
)(dχ
2
+ sinh
2
χ d
2
). (12.19)

345 12.2 Cosmological kinematics: observing the expanding universe
t
This is called the hyperbolic,oropen, Robertson–Walker model. Notice one peculiar
property. As the proper radial coordinate χ increases away from the origin, the circum-
ferences of spheres increase as sinh χ. Since sinh χ>χ for all χ>0, it follows that
these circumferences increase more rapidly with proper radius than in flat space. For this
reason this hypersurface is not realizable as a three-dimensional hypersurface in a four-
or higher-dimensional Euclidean space. That is, there is no picture which we can easily
draw such as that for the three-sphere. The space is call ‘open’ because, unlike for k =+1,
circumferences of spheres increase monotonically with χ : there is no natural end to the
space.
In fact, as we show in Exer. 8, § 12.6, this geometry is the geometry of a hypersurface
embedded in Minkowski spacetime. Specifically, it is a hypersurface of events that all have
the same timelike interval from the origin. Since this hypersurface has the same interval
from the origin in any Lorentz frame (intervals are Lorentz invariant), this hypersurface is
indeed homogeneous and isotropic.
Cosmological redshift as a distance measure
When studying small regions of the universe around the Sun, astronomers measure proper
distances to stars and other objects and express them in parsecs, as we have seen, or in the
multiples kpc and Mpc. But if the object is at a cosmological distance in a universe that
is expanding, then what we mean by distance is a little ambiguous, due to the long time it
takes light to travel from the object to us. Its separation from our location when it emitted
the light that we receive today may have been much less than its separation at present,
i.e. on the present hypersurface of constant time. Indeed, the object may not even exist
any more: all we know about it is that it existed at the event on our past light-cone when
it emitted the light we receive today. But between then and now it might have exploded,
collapsed, or otherwise changed dramatically. So the notion of the separation between us
and the object now is not as important as it might be for local measurements.
Instead, astronomers commonly use a different measurement of separation: the redshift
z of the spectrum of the light emitted by the object, let us say a galaxy. In an expanding
universe that follows Hubble’s Law, Eq. (12.1), the further away the galaxy is, the faster it is
receding from us, so the redshift is a nice monotonic measure of separation: larger redshifts
imply larger distances. Of course, as we noted in the discussion following Eq. (12.1), the
galaxy’s redshift contains an element due to its random local velocity; over cosmological
distances this is a small uncertainty, but for the nearby parts of the universe astronomers
use conventional distance measures, mainly Mpc, instead of redshift.
To compute the redshift in our cosmological models, let us assume that the galaxy has a
fixed coordinate position on some hypersurface at the cosmological time t at which it emits
the light we eventually receive at time t
0
. Recall our discussion of conserved quantities in
§ 7.4: if the metric is independent of a coordinate, then the associated covariant component
of momentum is constant along a geodesic. In the cosmological case, the homogeneity
of the hypersurfaces ensures that the covariant components of the spatial momentum of
the photon emitted by our galaxy are constant along its trajectory. Suppose that we place

346 Cosmology
t
ourselves at the origin of the cosmological coordinate system (since the cosmology is
homogeneous, we can put the origin anywhere we like), so that light travels along a radial
line θ = const., φ = const. to us. In each of the cosmologies the line-element restricted to
the trajectory has the form
0 =−dt
2
+ R
2
(t)dχ
2
. (12.20)
(To get this for the flat hypersurfaces, simply rename the coordinate r in the first part of
Eq. (12.15)toχ .) It follows that the relevant conserved quantity for the photon is p
χ
.
Now, the cosmological time coordinate t is proper time, so the energy as measured by a
local observer at rest in the cosmology anywhere along the trajectory is −p
0
. We argue in
Exer. 9, § 12.6, that conservation of p
χ
implies that p
0
is inversely proportional to R(t). It
follows that the wavelength as measured locally (in proper distance units) is proportional
to R(t), and hence that the redshift z of a photon emitted at time t and observed by us at
time t
0
is given by
l + z = R(t
0
)/R(t). (12.21)
It is important to keep in mind that this is just the cosmological part of any overall red-
shift: if the source or observer is moving relative to the cosmological rest frame, then there
will be a further factor of 1 + z
motion
multiplied into the right-hand-side of Eq. (12.24).
We now show that the Hubble parameter H(t) is the instantaneous relative rate of
expansion of the universe at time t:
H(t) =
˙
R(t)
R(t)
. (12.22)
Our galaxy at a fixed coordinate location χ is carried away from us by the cosmologi-
cal expansion. At the present time t
0
its proper distance d from us (in the constant-time
hypersurface) is the same for each of the cosmologies when expressed in terms of χ:
d
0
= R(t
0
)χ. (12.23)
It follows by differentiating this that the current rate of change of proper distance between
the observer at the origin and the galaxy at fixed χ is
v = (
˙
R/R)
0
d
0
= H
0
d
0
, (12.24)
where H
0
is the present value of the Hubble parameter. By comparison with Eq. (12.1), we
see that this is just the present value of the Hubble parameter
˙
R/R. We show in Exer. 10,
§ 12.6 that this velocity is just v = z, which is what is required to give the redshift z,

347 12.2 Cosmological kinematics: observing the expanding universe
t
provided the galaxy is not far away. In our cosmological neighborhood, therefore, the cos-
mological redshift is a true Doppler shift. Moreover, the redshift is proportional to proper
distance in our neighborhood, with the Hubble constant as the constant of proportionality.
We shall now investigate how various measures of distance depend on redshift when we
leave our cosmological neighborhood.
The scale factor of the Universe R(t) is related to the Hubble parameter by Eq. (12.22).
Integrating this for R gives
R(t) = R
0
exp
$
'
t
t
0
H(t
)dt
!
. (12.25)
The Taylor expansion of this is
R(t) = R
0
[1 + H
0
(t −t
0
) +
1
2
(H
2
0
+
˙
H
0
)(t −t
0
)
2
+···], (12.26)
where subscripted zeros denote quantities evaluated at t
0
. The time-derivative of the
Hubble parameter contains information about the acceleration or deceleration of the expan-
sion. Cosmologists sometimes replace
˙
H
0
with the dimensionless deceleration parameter,
defined as
q
0
=−R
0
¨
R
0
/
˙
R
2
0
=−
-
1 +
˙
H
0
/H
2
0
.
. (12.27)
The minus sign in the definition and the name ‘deceleration parameter’ reflect the assump-
tion, when this parameter was first introduced, that gravity would be slowing down the
cosmological expansion, so that q
0
would be positive. However, astronomers now believe
that the universe is accelerating, so the idea of a ‘deceleration parameter’ has gone out of
fashion. Nevertheless, any formula containing
˙
H
0
can be converted to one in terms of q
0
and vice-versa.
What does Hubble’s law, Eq. (12.1), look like to this accuracy? The recessional velocity
v is deduced from the redshift of spectral lines, so it is more convenient to work directly
with the redshift. Combining Eq. (12.25) with Eq. (12.21) we get
1 + z(t) = exp
$
−
'
t
t
0
H(t
)dt
!
. (12.28)
The Taylor expansion of this is
z(t) = H
0
(t
0
− t) +
1
2
(H
2
0
−
˙
H
0
)(t
0
− t)
2
+···. (12.29)
This is not directly useful yet, since we have no independent information about the time
t at which a galaxy emitted its light. Perhaps Eq. (12.29) is more useful when inverted to
give an expansion for the look-back proper time to an event with redshift z:
t
0
− t(z) = H
−1
0
z −
1
2
(1 −
˙
H
0
/H
2
0
)z
2
+···
. (12.30)
From the simple expansion
H(t) = H
0
+
˙
H
0
(t −t
0
) +···,

348 Cosmology
t
we can substitute in the first term of the previous equation and get an expansion for H as a
function of z:
H(z) = H
0
1 −
˙
H
0
H
2
0
z +···
. (12.31)
Note that Eq. (12.28) can also be inverted to give the exact and very simple relation
H(t) =−
˙z
1 + z
. (12.32)
Although cosmology is self-consistent only within a relativistic framework, it is never-
theless useful to ask how the expansion of the universe looks in Newtonian language. We
imagine a spherical region uniformly filled with galaxies, starting at some time with radi-
ally outward velocities that are proportional to the distance from the center of the sphere.
If we are not near the edge – and of course the edge may be much too far away for us
to see today – then we can show that the expansion is homogeneous and isotropic about
every point. The galaxies just fly away from one another, and the Hubble constant is the
scale for the initial velocity: it is the radial velocity per unit distance away from the origin.
The problem with this Newtonian model is not that it cannot describe the local state of the
universe, it is that, with gravitational forces that propagate instantaneously, the dynamics
of any bit of the universe depends on the structure of this cloud of galaxies arbitrarily far
away. Only in a relativistic theory of gravity can we make sense of the dynamical evolution
of the universe. This is a subject we will study below.
When light is redshifted, it loses energy. Where does this energy go? The fully relativistic
answer is that it just goes away: since the metric depends on time, there is no conservation
law for energy along a geodesic. Interestingly, in the Newtonian picture of the universe just
described, the redshift is just caused by the different velocities of the diverging galaxies
relative to one another. As the photon moves outward in the expanding cloud, it finds itself
passing galaxies that are moving faster and faster relative to the center. It is not surprising
that they measure the energy of the photon to be smaller and smaller as it moves outwards.
Cosmography: measures of distance in the universe
Cosmography refers to the description of the expansion of the universe and its history.
In cosmography we do not yet apply the Einstein equations to explain the motion of the
universe, instead we simply measure its expansion history. The language of cosmography
is the language of distance measures and the evolution of the Hubble parameter.
By analogy with Eq. (12.1), we would like to replace t in Eq. (12.29) with distance. But
what measure of distance is suitable over vast cosmological separations? Not coordinate
distance, which would be unmeasurable. What about proper distance? The proper distance
between the events of emission and reception of the light is zero, since light travels on
null lines. The proper distance between the emitting galaxy and us at the present time is

349 12.2 Cosmological kinematics: observing the expanding universe
t
also unmeasurable: in principle, the galaxy may not even exist now, perhaps because of a
collision with another galaxy. To get out of this difficulty, let us ask how distance crept into
Eq. (12.1) in the first place.
Distances to nearby galaxies are almost always inferred from luminosity measurements.
Consider an object whose distance d is known, which is at rest, and which is near enough
to us that we can assume that space is Euclidean. Then a measurement of its flux F leads
to an inference of its absolute luminosity:
L = 4πd
2
F (12.33)
Alternatively, if L is known, then a measurement of F leads to the distance d. The role of d
in Eq. (12.1) is, then, as a replacement for the observable (L/F)
1/2
.
Astronomers have used brightness measurements to build up a carefully calibrated cos-
mological distance ladder to measure the scale of the universe. For each step on this ladder
they identify what is called a standard candle, which is a class of objects whose abso-
lute luminosity L is known (say from a theory of their nature or from reliably calibrated
distances to nearby examples of this object). As their ability to see to greater and greater
distances has developed, astronomers have found new standard candles that they could cali-
brate from previous ones but that were bright enough to be seen to greater distances than
the previous ones. The distance ladder starts at the nearest stars, the distances to which can
be measured by parallax (independently of luminosity), and continues all the way to very
distant high-redshift galaxies.
In the spirit of such measurements, cosmologists define the luminosity distance d
L
to
any object, no matter how distant, by inverting Eq. (12.33):
d
L
=
L
4πF
1/2
. (12.34)
The luminosity distance is often the observable that can be directly measured by
astronomers: if the intrinsic luminosity L is known or can be inferred, then a measure-
ment of its brightness F determines the luminosity distance. The luminosity distance is
the proper distance the object would have in a Euclidean universe if it were at rest with
respect to us, if it had an intrinsic luminosity L, and if we received an energy flux F from
it. However, in an expanding cosmology this will not generally be the proper distance to
the object.
We shall now find the relation between luminosity distance and the cosmological scales
we have just introduced. Consider an object emitting with luminosity L at a time t
e
. What
flux do we receive from it at the later time t
0
? Suppose for simplicity that the object gives
off only photons of frequency ν
e
at time t
e
. (This frequency will drop out in the end, so our
result will be perfectly general.) In a small interval of time δt
e
the object emits
N = Lδt
e
/hν
e
(12.35)
photons in a spherically symmetric manner. To find the flux we receive, we must calculate
the area of the sphere that these photons occupy at the time we observe them.

350 Cosmology
t
We place the object at the origin of the coordinate system, and suppose that we sit
at coordinate position r in this system, as given in Eq. (12.13). Then when the photons
reach our coordinate distance from the emitting object, the proper area of the sphere they
occupy is given by integrating over the sphere the solid-angle part of the line-element in
Eq. (12.13), which is R
2
0
r
2
d
2
. The integration is just on the spherical angles and produces
the area:
A = 4πR
2
0
r
2
. (12.36)
Now, the photons have been redshifted by the amount (1 + z) = R
0
/R(t
e
) to frequency ν
0
:
hν
0
= hν
e
/(1 + z). (12.37)
Moreover, they arrive spread out over a time δt
0
, which is also stretched by the redshift:
δt
0
= δt
e
(1 + z). (12.38)
The energy flux at the observation time t
0
is thus Nhν
0
/(Aδt
0
), from which it follows that
F = L/A(1 + z)
2
. (12.39)
From Eq. (12.34), we then find
d
L
= R
0
r(1 +z). (12.40)
To use this, we need to know the comoving source coordinate location r as a function
of the redshift z of the photon the source emitted. This comes from solving the equation
of motion of the photon. In this case, all we have to do is use Eq. (12.13) with ds
2
= 0(a
photon world line) and d
2
= 0 (photon traveling on a radial line from its emitter to the
observer at the center of the coordinates). This leads to the differential equation
dr
1 − kr
2
1/2
=−
dt
R(t)
=
dz
R
0
H(z)
, (12.41)
where the last step follows from differentiating Eq. (12.21). This equation involves the
curvature parameter k,butforsmallr and z the curvature will come into the solution only at
second order. If we ignore this at present and work only to first order beyond the Euclidean
relations, it is not hard to show that
d
L
= R
0
r(1 +z) =
z
H
0
%
1 +
1 +
1
2
˙
H
0
H
2
0
z
&
+···. (12.42)
If we can measure the luminosity distances and redshifts of a number of objects, then
we can in principle measure
˙
H
0
. Measurements of this kind led to the discovery of the
accelerating expansion of the universe (below).
Another convenient measure of distance is the angular diameter distance. This is based
on another way of measuring distances in a Euclidean space: the angular size θ of an object
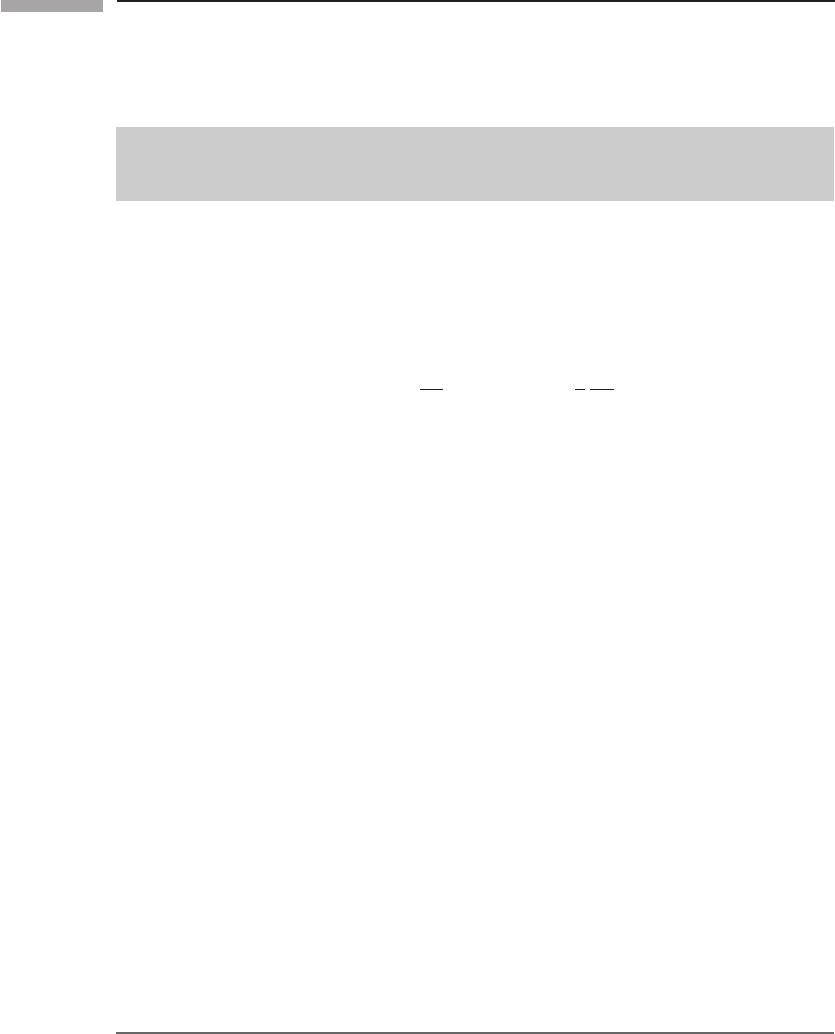
351 12.2 Cosmological kinematics: observing the expanding universe
t
at a distance d can be inferred if we know the proper diameter D of the object transverse to
the line of sight, θ = D/d. This leads to the definition of the angular diameter distance d
A
to an object anywhere in the universe:
d
A
= D/θ . (12.43)
The dependence of d
A
on redshift z is explored in Exer. 12, § 12.6. The result is
d
A
= R
e
r = (1 + z)
−2
d
L
, (12.44)
where R
e
is the scale factor of the universe when the photon was emitted. The analogous
expression to Eq. (12.42)is
d
A
= R
0
r/(1 +z) =
z
H
0
%
1 +
−1 +
1
2
˙
H
0
H
2
0
z
&
+···. (12.45)
There are situations where we have in fact an estimate of the comoving diameter D of
an emitter. In particular, the temperature irregularities in maps of the cosmic microwave
background radiation (see below) have a length scale that is determined by the physics of
the early universe.
Although we have provided small-z expansions for many interesting measures, it is
important to bear in mind that astronomers today can observe objects out to very high
redshifts. Some galaxies and quasars are known at redshifts greater than z = 6. The cos-
mological microwave background, which we will discuss below, originated at redshift
z ∼ 1000, and is our best tool for understanding the Big Bang. Even so, the universe
was already some 300 000 years old at that redshift. Sometime in the future, gravitational
wave detectors may detect random radiation from the Big Bang itself, originating when the
universe was only a fraction of a second old.
The derivation of Eq. (12.42) illustrates a point which we have encountered before: in
the attempt to translate the nonrelativistic formula v = Hd into relativistic language, we
were forced to re-think the meaning of all the terms in the equations and to go back to the
quantities we can directly measure. If the study of GR teaches us only one thing, it should
be that physics rests ultimately on measurements: concepts like distance, time, velocity,
energy, and mass are derived from measurements, but they are often not the quantities
directly measured, and our assumptions about their global properties must be guided by a
careful understanding of how they are related to measurements.
The universe is accelerating!
The most remarkable cosmographic result since Hubble’s original work was the discovery
that the expansion of the universe is not slowing down, but rather speeding up. This was
done by essentially making a plot of the luminosity distance against redshift, but where
luminosities are given in magnitudes. This is called the magnitude–redshift diagram, and
we derive its low-z expansion in Exer. 13, § 12.6. Two teams of astronomers, called the

352 Cosmology
t
High-Z Supernova Search Team (Riess et al., 1998) and the Supernova Cosmology Project
(Perlmutter et al., 1999), respectively, used supernova explosions of Type Ia as standard
candles out to redshifts of order 1. Although there was considerable scatter among the data
points, both teams found that the best fit to the data was a universe that was speeding up and
not slowing down. The data from the High-Z Team are shown in Fig. 12.3. See Filippenko
(2008) for a full discussion.
The top diagram shows the flux (magnitude) measurement for each of the supernovae
in the sample, along with error bars. The trend seems to curve upwards, meaning that at
high redshifts the supernovae are dimmer than expected. This would happen if the universe
were speeding up, because the supernovae would simply be further away than expected.
Three possible fits are shown, and the best one has a large positive cosmological constant,
which we shall see below is the simplest way, within Einstein’s equations, that we can
accommodate acceleration. The lower diagram shows the same data but plotting only the
residuals from the fit to a flat universe. This shows more clearly how the data favor the
curve for the accelerating universe.
These studies were the first strong evidence for acceleration, but by now there are several
lines of investigation that lead to the same conclusion. Astronomers initially resisted the
conclusion, because it undermines a basic assumption we have always made about gravity,
that it is universally attractive. If the energy density of the universe exerts attractive gravity,
34
36
38
40
42
44
Ω
M
=
0.24, Ω
Λ
=
0.76
Ω
M
=
0.20, Ω
Λ
=
0.00
Ω
M
=
1.00, Ω
Λ
=
0.00
m-M (mag)
MLCS
0.01 0.10 1.00
z
–0.5
0.0
0.5
Δ(m-M) (mag)
t
Figure 12.3
The trend of luminosity versus redshift for Type Ia supernovae is fit best with an accelerating
universe. The lower part of this curve determines H
0
, the upper part demonstrates acceleration.
(High-Z Supernova Search Team: Riess, et al, 1998.)
