Schutz B. A first course in general relativity

Подождите немного. Документ загружается.

303 11.2 Nature of the surface r = 2M

Much needs to be said about this. First, two light cones are drawn for illustration. Any

◦

line is a radial null line. Second, only u and υ are plotted: θ and φ are suppressed;

therefore each point is really a two sphere of events. Third, lines of constant r are hyper-

bolae, as is clear from Eq. (11.68). For r > 2M, these hyperbolae run roughly vertically,

being asymptotic to the 45

◦

line from the origin u = υ = 0. For r < 2M, the hyperbolae

run roughly horizontally, with the same asymptotes. This means that for r < 2M, a timelike

line (conﬁned within the light cone) cannot remain at constant r. This is the result we had

before. The hyperbola r = 0 is the end of the spacetime, since a true singularity is there.

Note that although r = 0 is a ‘point’ in ordinary space, it is a whole hyperbola here. How-

ever, not too much can be made of this, since it is a singularity of the geometry: we should

not glibly speak of it as a part of spacetime with a well-deﬁned dimensionality.

Our fourth remark is that lines of constant t, being orthogonal to lines of constant r,

are straight lines in this diagram, radiating outwards from the origin u = υ = 0. (They are

orthogonal to the hyperbolae r = const. in the spacetime sense of orthogonality; recall

our diagrams in § 1.7 of invariant hyperbolae in SR, which had the same property of

being orthogonal to lines radiating out from the origin.) In the limit as t →∞, these lines

approach the 45

◦

line from the origin. Since all the lines t = const. pass through the ori-

gin, the origin would be expanded into a whole line in a (t, r) coordinate diagram like

Fig. 11.10, which is what we guessed after discussing that diagram. A world line cross-

ing this t =∞line in Fig. 11.11 enters the region in which r is a time coordinate, and so

cannot get out again. The true horizon, then, is this line r = 2M, t =+∞.

Fifth, since for a distant observer t really does measure proper time, and an object that

falls to the horizon crosses all the lines t = const. up to t =∞, a distant observer would

conclude that it takes an inﬁnite time for the infalling object to reach the horizon. We have

already drawn this conclusion before, but here we see it displayed clearly in the diagram.

There is nothing ‘wrong’ in this statement: the distant observer does wait an inﬁnite time

to get the information that the object has crossed the horizon. But the object reaches the

horizon in a ﬁnite time on its own clock. If the infalling object sends out radio pulses each

time its clock ticks, then it will emit only a ﬁnite number before reaching the horizon, so

the distant observer can receive only a ﬁnite number of pulses. Since these are stretched

out over a very large amount of the distant observer’s time, the observer concludes that

time on the infalling clock is slowing down and eventually stopping. If the infalling ‘clock’

is a photon, the observer will conclude that the photon experiences an inﬁnite gravitational

redshift. This will also happen if the infalling ‘object’ is a gravitational wave of short

wavelength compared to the horizon size.

Sixth, this horizon is itself a null line. This must be the case, since the horizon is the

boundary between null rays that cannot get out and those that can. It is therefore the path

of the ‘marginal’ null ray. Seventh, the 45

◦

lines from the origin divide spacetime up into

four regions, labeled I, II, III, IV. Region I is clearly the ‘exterior’, r > 2M, and region II

is the interior of the horizon. But what about III and IV? To discuss them is beyond the

scope of this publication (see Misner et al. 1973, Box 33.2G and Ch. 34; and Hawking and

Ellis 1973), but one remark must be made. Consider the dashed line in Fig. (11.11), which

could be the path of an infalling particle. If this black hole were formed by the collapse of

a star, then we know that outside the star the geometry is the Schwarzschild geometry, but

304 Schwarzschild geometry and black holes

inside it may be quite different. The dashed line may be taken to be the path of the surface

of the collapsing star, in which case the region of the diagram to the right of it is outside

the star and so correctly describes the spacetime geometry, but everything to the left would

be inside the star (smaller r) and hence has possibly no relation to the true geometry of

the spacetime. This includes all of regions III and IV, so they are to be ignored by the

astrophysicist (though they can be interesting to the mathematician!). Note that parts of

I and II are also to be ignored, but there is still a singularity and horizon outside the star.

The eighth and last remark we will make is that the coordinates u and υ are not par-

ticularly good for describing the geometry far from the star, where g

and g

υυ

fall off

exponentially in r. The coordinates t and r are best there; indeed, they were constructed in

order to be well behaved there. But if we is interested in the horizon, then we use u and v.

11.3 G e n era l b la c k hol e s

Formation of black holes in general

The phenomenon of the formation of a horizon has to do with the collapse of matter to

such small dimensions that the gravitational ﬁeld traps everything within a certain region,

which is called the interior of the horizon. We have explored the structure of the black

hole in one particular case – the static, spherically symmetric situation – but the formation

of a horizon is a much more general phenomenon. When we discuss astrophysical black

holes in § 11.4 we will address the question of how Nature might arrange to get so much

mass into such a small region. But it should be clear that, in the real world, black holes are

not formed from perfectly spherical collapse. Black holes form in complicated dynamical

circumstances, and after they form they continue to participate in dynamics: as members

of binary systems, as centers of gas accretion, as sources of gravitational radiation. In this

section we learn how to deﬁne black holes and what we know about them in general.

The central, even astonishing property of the Schwarzschild horizon is that anything

that crosses it can not get back outside it. The deﬁnition of a general horizon (called an

event horizon) focuses on this property. An event horizon is the boundary in spacetime

between events that can communicate with distant observers and events that cannot. This

deﬁnition assumes that distant observers exist, that the spacetime is asymptotically ﬂat,

as deﬁned in § 8.4. And it permits the communication to take an arbitrarily long time: an

event is considered to be outside the horizon provided it can emit a photon in even just one

special direction that eventually makes it out to a distant observer. The most important part

of the deﬁnition to think about is that the horizon is a boundary in spacetime, not just in

the space deﬁned by one moment of time. It is a three-dimensional surface that separates

the events of spacetime into two regions: trapped events inside the horizon and untrapped

events outside.

Since no form of communication can go faster than light, the test of whether events can

communicate with distant observers is whether they can send light rays, that is whether

there are null rays that can get arbitrarily far away. As the boundary between null rays that

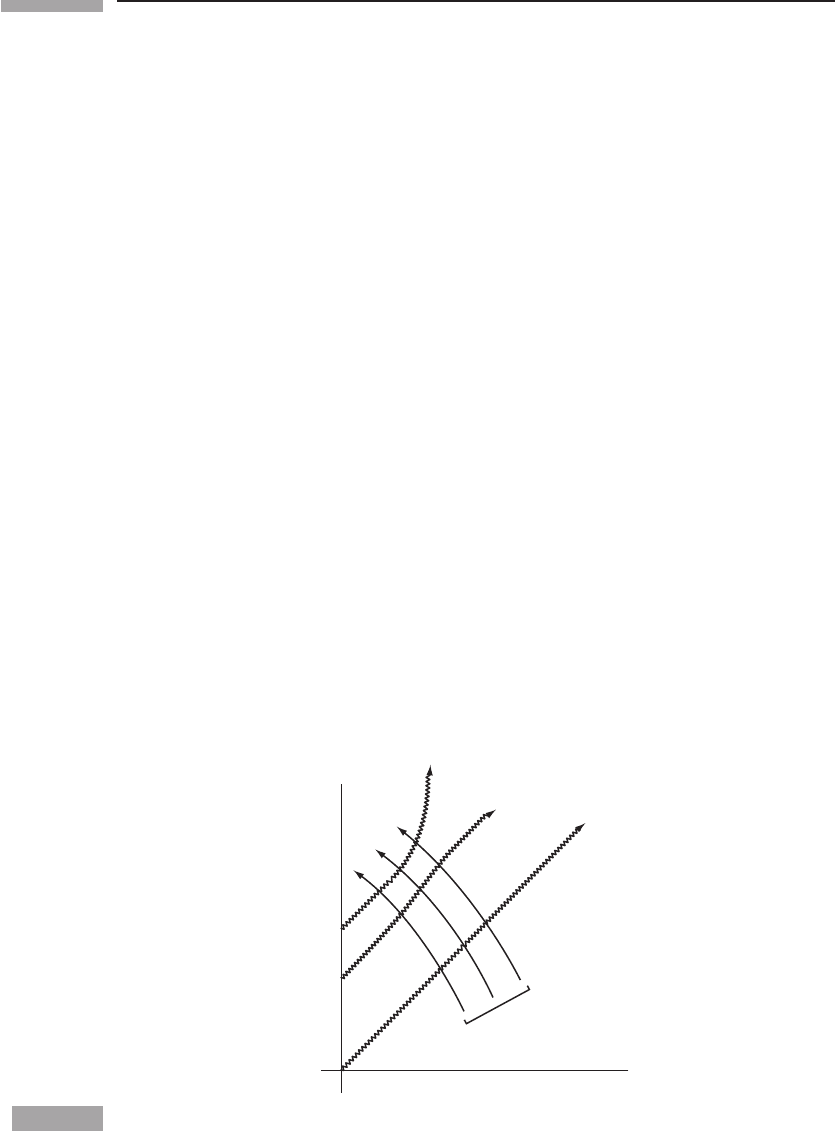
305 11.3 General black holes

can escape and null rays that are trapped, the horizon itself is composed of null world lines.

These are the marginally trapped null rays, the ones that neither move away to inﬁnity nor

fall inwards. By deﬁnition these marginal null rays stay on the horizon forever, because if

a ray were to leave it toward the exterior or interior, then it would not mark the horizon.

It is not hard to see that this deﬁnition ﬁts the Schwarzschild horizon, which is static and

unchanging, but when we consider dynamical situations there are some surprises.

The formation of a horizon from a situation where there is initially no black hole illus-

trates well the dynamical nature of the horizon. Consider the collapse of a spherical star to

form a black hole. In the end there is a static Schwarzschild horizon, but before that there

is an intermediate period of time in which the horizon is growing from zero radius to its

full size. This is easy to see by considering Fig. 11.12, which illustrates (very schemati-

cally) the collapsing situation. (The time coordinate is a kind of Schwarzschild time, but it

isn’t to be taken too literally.) As matter falls in, the trajectories of photons that start from

the center of the collapsing star (wavy lines) are more and more affected. Photon (a) gets

out with little trouble, photon (b) has some delay, and photon (c) is the ‘marginal’ one,

which just gets trapped and remains on the Schwarzschild horizon. Anything later than (c)

is permanently trapped, anything earlier gets out. So photon (c) does in fact represent the

horizon at all times, by deﬁnition, since it is the boundary between trapped and untrapped.

Thus, we see the horizon grow from zero radius to 2M by watching photon (c)’s progress

outwards. For this spherically symmetric situation, if we knew the details of the collapse,

we could easily determine the position of the horizon. But if there were no symmetry –

particularly if the collapse produced a large amount of gravitational radiation – then the

calculation would be far more difﬁcult, although the principle would be the same.

As a more subtle example of a dynamical horizon, consider what happens to the

Schwarzschild horizon of the ‘ﬁnal’ black hole in Fig. 11.12 if at a much later time some

more gas falls in (not illustrated in the ﬁgure). For simplicity, we again assume the infalling

World lines of

collapsing matter

(c)

(b)

(a)

Figure 11.12

Schematic spacetime diagram of spherical collapse. Light ray (a) hardly feels anything, (b)is

delayed, and (c) is marginally trapped. The horizon is deﬁned as the ray (c), so it grows

continuously from zero radius as the collapse proceeds.

306 Schwarzschild geometry and black holes

gas is perfectly spherical. Let the mass of the hole before the gas falls in be called M

.The

surface r = 2M

is static and appears to be the event horizon: photons inside it fall towards

the singularity at the center, and photons inﬁnitesimally outside it gradually move further

and further away from it. But then the new gas falls across this surface and increases the

mass of the hole to M

. Clearly, the new ﬁnal state will be a Schwarzschild solution of

mass M

, where the larger surface r = 2M

looks like an event horizon. It consists of null

rays neither falling in nor diverging outwards. Now, what is the history of these rays? What

happens if we trace backwards in time along a ray that just stays at r = 2M

?Wewould

ﬁnd that, before the new gas arrived, it was one of those null world lines just outside the

surface r = 2M

, one of the rays that were very gradually diverging from it. The extra mass

has added more gravitational attraction (more curvature) that stopped the ray from moving

away and now holds it exactly at r = 2M

. Moreover, the null rays that formed the static

surface r = 2M

before the gas fell in are now inside r = 2M

and are therefore falling

toward the singularity, again pulled in by the gravitational attraction of the extra mass. The

boundary in spacetime between what is trapped and what is not consists therefore of the

null rays that in the end sit at r = 2M

, including their continuation backwards in time.

The null rays on r = 2M

were not actually part of the true horizon of spacetime even at

the earlier time: they are just trapped null rays that took a long time to ﬁnd out that they

were trapped! Before the gas fell in, what looked like a static event horizon (r = 2M

)

was not an event horizon at all, even though it was temporarily a static collection of null

rays. Instead, the true boundary between trapped and untrapped was even at that early time

gradually expanding outwards, traced by the null world lines that eventually became the

surface r = 2M

This example illustrates the fact that the horizon is not a location in space but a boundary

in spacetime. It is not possible to determine the location of the horizon by looking at a

system at one particular time; instead we must look at its entire evolution in time, ﬁnd out

which null rays eventually really do escape and which ones are trapped, and then trace out

the boundary between them. The horizon is a property of the spacetime as a whole, not of

space at any one moment of time. In our example, if many years later some further gas falls

into the hole, then we would ﬁnd that even those null rays at r = 2M

would actually be

trapped and would not have been part of the true event horizon after all. The only way to

ﬁnd the true horizon is to know the entire future evolution of the spacetime and then trace

out the boundary between trapped and untrapped regions.

This deﬁnition of the event horizon is mathematically consistent and logical, but it is

difﬁcult to work with in practical situations. If we know only a limited amount about a

spacetime, it can in principle be impossible to locate the horizon. For example, computer

simulations of solutions of Einstein’s equations containing black holes cannot run forever,

so they don’t have all the information needed even to locate the horizons of their black

holes. So physicists also work with another kind of surface that can be deﬁned at any

one moment of time. It uses the other property of the Schwarzschild horizon, that it is

a static collection of null rays. Physicists deﬁne a locally trapped surface tobeatwo-

dimensional surface at any particular time whose outwardly directed null rays are neither

expanding nor contracting at that particular moment. Locally trapped surfaces are always

inside true horizons in dynamical situations, just as r = 2M

turned out to be inside the

307 11.3 General black holes

true horizon, but very often they are so close to the true horizon that they offer an excellent

approximation to it.

General properties of black holes

While the detailed structure of an event horizon is not easy to compute, some important

general properties of horizons are understood, and they underpin the conﬁdence with which

astronomers now employ black holes in models of complex astrophysical phenomena. Here

are some important theorems and conjectures.

(1) It is believed that any horizon will eventually become stationary, provided that it is

not constantly disturbed by outside effects like accretion. So an isolated black hole

should become stationary. (The calculations in item (3) below support this idea.) The

stationary horizons, by contrast with nonstationary ones, are completely known. The

principal result is that a stationary vacuum black hole is characterized by just two

numbers: its total mass M and total angular momentum J. These parameters are deﬁned

not by any integrals over the ‘interior’ of the horizon, but by the gravitational ﬁeld far

from the hole. We have deﬁned the mass M of any metric in this fashion in § 8.4, and

in Exer. 19, § 8.6, we have seen how J can be similarly deﬁned. The unique stationary

vacuum black hole is the Kerr solution, Eq. (11.71), which we study in detail below. If

the angular momentum is zero, the Kerr solution becomes the Schwarzschild metric.

This uniqueness theorem results from work done by Hawking (1972), Carter (1973),

and Robinson (1975). See Chru

sciel (1996) and Heusler (1998) for reviews.

(2) If the black hole is not in vacuum, its structure may be more general. It may carry an

electric charge Q and, in principle, a magnetic monopole moment F, although mag-

netic monopoles are not found in Nature. Both of these charges can be measured by

Gauss’ law integrals over surfaces surrounding the hole and far from it. It is also felt

that collapse is unlikely to lead to a signiﬁcant residual charge Q, so astrophysicists

normally take only M and J to be nonzero. But other kinds of ﬁelds, such as those

encountered in particle physics theories, can add other complications: self-gravitating

interacting scalar ﬁelds, Yang-Mills ﬁelds, and so on. See Heusler (1998) for a review.

Again, these complications are not usually thought to be relevant in astrophysics. What

may be relevant, however, is the distortion of the horizon produced by the tidal effect

of matter surrounding the black hole. If a massive stationary disk of gas surrounds the

hole, then the metric will not be exactly Kerr (e.g. Will 1974, 1975; Ansorg 2005).

(3) If gravitational collapse is nearly spherical, then all nonspherical parts of the mass

distribution – quadrupole moment, octupole moment – except possibly for angular

momentum, are radiated away in gravitational waves, and a stationary black hole of

the Kerr type is left behind. If there is no angular momentum, a Schwarzschild hole

is left behind (Price 1972a, b). The Kerr black hole appears to be stable against all

perturbations, but the proof is not quite complete (Whiting 1989, Beyer 2001).

(4) An important general result concerning nonstationary horizons is the area theorem of

Hawking (Hawking and Ellis 1973): in any dynamical process involving black holes,

the total area of all the horizons cannot decrease in time. We saw this in a qualitative

308 Schwarzschild geometry and black holes

way in our earlier discussion of how to deﬁne a horizon when matter is falling into

a black hole: the area is actually increasing during the period before the infalling gas

reaches the hole. We shall see below how to quantify this theorem by calculating the

area of the Kerr horizon. The area theorem implies that, while two black holes can

collide and coalesce, a single black hole can never bifurcate spontaneously into two

smaller ones. (A restricted proof of this is in Exer. 26, § 11.7 using the Kerr area

formula below; a full proof is outlined in Misner et al. 1973, Exer. 34.4, and requires

techniques beyond the scope of this book.) The theorem assumes that the local energy

density of matter in spacetime (ρ) is positive. The analogy between an ever-increasing

area and the ever-increasing entropy of thermodynamics has led to the development

of black-hole thermodynamics, and the understanding that black holes ﬁt into thermal

physics in a very natural way. The entropy associated with the area of the horizon is

given in Eq. (11.114). The key to this association is the demonstration by Hawking that

quantum mechanics can lead to spontaneous radiation from a black hole. The radiation

has a thermal spectrum, which leads to a temperature and hence an entropy for the

horizon. This violation of the area theorem by quantum effects happens because in

quantum mechanics, energies are not always required to be positive. We study this

Hawking radiation in § 11.5 below.

(5) Inside the Schwarzschild and Kerr horizons there are curvature singularities where the

curvature, and hence the tidal gravitational force, becomes inﬁnite. General theorems,

mostly due to Hawking and Penrose, imply that any horizon will contain a singular-

ity within it of some kind (Hawking and Ellis 1973). But it is not known whether

such singularities will always have inﬁnite curvature; all that is known is that infalling

geodesics are incomplete and cannot be continued for an inﬁnite amount of proper

time or afﬁne distance. The existence of these singularities is generally regarded as

a serious shortcoming of general relativity, that its predictions have limited validity

in time inside horizons. Many physicists expect this shortcoming to be remedied by

a quantum theory of gravity. The uncertainty principle of quantum mechanics, so the

expectation goes, will make the singularity a little ‘fuzzy’, the tidal forces will not

quite reach inﬁnite strength, and the waveform will continue further into the future. In

the absence of an acceptable theory of quantum gravity, this remains only a hope, but

there are some computations in restricted quantum models that are suggestive that this

might in fact happen (Bojowald 2005, Ashtekar and Bojowald 2006).

(6) The generic existence of singularities inside horizons, hidden from the view of distant

observers, prompts the question of whether there can be so-called naked singularities,

that is singularities outside horizons. These would be far more problematic for gen-

eral relativity, for it would mean that situations could arise in which general relativity

could make no predictions beyond a certain time even for normal regions of space-

time. Having singularities in unobservable regions inside horizons is bad enough, but

if singularities arose outside horizons, general relativity would be even more ﬂawed. In

response to this concern, Penrose (1979) formulated the cosmic censorship conjecture,

according to which no naked singularities can arise out of nonsingular initial condi-

tions in asymptotically ﬂat spacetimes. Penrose had no proof of this, and offered it as a

challenge to relativity theorists. Even today there is considerable debate over whether,

309 11.3 General black holes

and in exactly what formulation, the conjecture is true (Berger 2002, Cru

sciel 1991,

Rendall 2005). One naked singularity seems inescapable in general relativity: the Big

Bang of standard cosmology is naked to our view. If the universe re-collapses, there

will similarly be a Big Crunch in the future of all our world lines. These issues are

discussed in the next chapter.

Item (1) above is truly remarkable: a massive black hole, possibly formed from 10

individual atoms and molecules – whose history as a gas may have included complex gas

motions, shock waves, magnetic ﬁelds, nucleosynthesis, and all kinds of other complica-

tions – is described fully and exactly by just two numbers, its mass and spin. The horizon

and the entire spacetime geometry outside it depend on just these two numbers. All the

complication of the formation process is effaced, forgotten, reduced to two simple num-

bers. No other macroscopic body is so simple to describe. We might characterize a star by

its mass, luminosity, and color, but these are just a start, just categories that contain an inﬁ-

nite potential variety within them. Stars can have magnetic ﬁelds, spots, winds, differential

rotation, and many other large-scale features, to say nothing of the different motions of

individual atoms and ions. While this variety may not be relevant in most circumstances,

it is there. For a black hole, it is simply not there. There is nothing but mass and spin, no

individual structure or variety revealed by microscopic examination of the horizon (see the

reaction of Chandrasekhar to this fact, quoted in § 11.4 below). In fact, the horizon is not

even a real surface, it is just a boundary in empty space between trapped and untrapped

regions. The fact that no information can escape from inside the hole means that no infor-

mation about what fell in is visible from the outside. The only quantities that remain are

those that are conserved by the fundamental laws of physics: mass and angular momentum.

Kerr black hole

The Kerr black hole is axially symmetric but not spherically symmetric (that is rotationally

symmetric about one axis only, which is the angular-momentum axis), and is characterized

by two parameters, M and J. Since J has dimension m

, we conventionally deﬁne

a := J/M, (11.70)

which then has the same dimensions as M. The line element is

=−

 − a

sin

− 2a

2Mr sin

dt dφ

+ a

)

− a

 sin

sin

θ dφ



+ ρ

dθ

, (11.71)

where

 := r

− 2Mr + a

:= r

+ a

cos

θ. (11.72)

The coordinates are called Boyer–Lindquist coordinates; φ is the angle around the axis of

symmetry, t is the time coordinate in which everything is stationary, and r and θ are similar

310 Schwarzschild geometry and black holes

to the spherically symmetric r and θ but are not so readily associated to any geometrical

deﬁnition. In particular, since there are no metric two-spheres, the coordinate r cannot be

deﬁned as an ‘area’ coordinate as we did before. The following points are important:

(1) Surfaces t = const., r = const. do not have the metric of the two-sphere, Eq. (10.2).

(2) The metric for a = 0 is identically the Schwarzschild metric.

(3) There is an off-diagonal term in the metric, in contrast to Schwarzschild:

tφ

=−a

2Mr sin

, (11.73)

which is

the coefﬁcient of dt dφ in Eq. (11.71) because the line element contains two

terms,

tφ

dt dφ +g

φt

dφ dt = 2g

tφ

dφ dt,

by the symmetry of the metric. Any axially symmetric, stationary metric has preferred

coordinates t and φ, namely those which have the property g

αβ,t

= 0 = g

αβ,φ

.Butthe

coordinates r and θ are more-or-less arbitrary, except that they may be chosen to be

(i) orthogonal to t and φ (g

= g

rφ

= g

θt

= g

θφ

= 0) and (ii) orthogonal to each other

θr

= 0). In general, we cannot choose t and φ orthogonal to each other (g

tφ

= 0).

Thus Eq. (11.71) has the minimum number of nonzero g

αβ

(see Carter 1969).

Dragging of inertial frames

The presence of g

tφ

= 0 in the metric introduces qualitatively new effects on particle tra-

jectories. Because g

αβ

is independent of φ, a particle’s trajectory still conserves p

.But

now we have

= g

φα

= g

φφ

+ g

φt

, (11.74)

and similarly for the time components:

= g

tα

= g

+ g

tφ

. (11.75)

Consider a zero angular-momentum particle, p

= 0. Then, using the deﬁnitions (for

nonzero rest mass)

= m dt/dτ , p

= m dφ/dτ , (11.76)

we ﬁnd that the particle’s trajectory has

dφ

φt

:= ω(r, θ ). (11.77)

This equation deﬁnes what we mean by ω, the angular velocity of a zero angular-

momentum particle. We shall ﬁnd ω explicitly for the Kerr metric when we obtain the

contravariant components g

φt

and g

below. But it is clear that this effect will be present

in any metric for which g

tφ

= 0, which in turn happens whenever the source is rotating

(e.g. a rotating star as in Exer. 19, § 8.6). So we have the remarkable result that a particle

311 11.3 General black holes

dropped ‘straight in’ (p

= 0) from inﬁnity is ‘dragged’ just by the inﬂuence of gravity so

that it acquires an angular velocity in the same sense as that of the source of the metric

(we’ll see below that, for the Kerr metric, ω hasthesamesignasa). This effect weakens

with distance (roughly as 1/r

;seeEq.(11.90) below for the Kerr metric), and it makes the

angular momentum of the source measurable in principle, although in most situations the

effect is small, as we have seen in Exer. 19, § 8.6. This effect is often called the dragging

of inertial frames.

This effect has a close analogy with magnetism. Newtonian gravity is, of course, very

similar to electrostatics, with the sign change that ensures that ‘charges’ of the same sign

attract one another. In electromagnetism, a spinning charge creates additional effects which

we call magnetism. Here we have the gravitational analog, the gravitational effects due to

a spinning mass. For that reason these effects are called gravitomagnetism. The analogy

between gravitomagnetism and standard magnetism is perhaps easier to see in the Lense–

Thirring effect: a gyroscope placed in orbit around a rotating star will precess by a small

amount that is proportional to the angular momentum of the star, just as a spinning electron

precesses if it orbits through a magnetic ﬁeld.

Small as it is, the Lense–Thirring effect created by the spin of the Earth has been mea-

sured. Detailed studies of the orbits of two geodesy satellites have so far been able to

verify that the effect is as predicted by general relativity, with an accuracy at the 20% level

(Ciufolini et al., 2006). An order of magnitude improvement could be made with an addi-

tional satellite in a specially chosen orbit. In addition, a satellite experiment called Gravity

Probe B (GP-B), which has measured the precession of on-board gyroscopes, is currently

(2008) analyzing its data and is expected to report soon, hopefully with errors below the

10% level. GP-B is one of the most sensitive and high-precision experiments ever per-

formed in orbit. Gravitomagnetic effects are regularly taken into account in modeling the

details of the emission of X-rays near black holes (e.g. Brenneman and Reynolds 2006),

and they may also soon be seen in the double pulsar system PSR J0737-3039 referred to

earlier in this chapter.

Ergoregion

Consider photons emitted in the equatorial plane (θ = π/2) at some given r. In particular,

consider those initially going in the ±φ-direction, that is tangent to a circle of constant r.

Then they generally have only dt and dφ nonzero on the path at ﬁrst and since ds

= 0, we

have

0 = g

+ 2g

tφ

dt dφ +g

φφ

dφ

⇒

dφ

=−

τφ

φφ



tφ

φφ



−

φφ

1/2

. (11.78)

Now, a remarkable thing happens if g

= 0: the two solutions are

dφ

= 0 and

dφ

=−

tφ

φφ

. (11.79)

312 Schwarzschild geometry and black holes

We will see below that for the Kerr metric the second solution gives dφ/dt the same sign

as the parameter a, and so represents the photon sent off in the same direction as the

hole’s rotating. The other solution means that the other photon – the one sent ‘backwards’–

initially doesn’t move at all. The dragging of orbits has become so strong that this photon

cannot move in the direction opposite the rotation. Clearly, any particle, which must move

slower than a photon, will therefore have to rotate with the hole, even if it has an angular

momentum arbitrarily large in the opposite sense to the hole’s!

We shall see that the surface where g

= 0 lies outside the horizon; it is called the

ergosphere. It is sometimes also called the ‘static limit’, since inside it no particle can

remain at ﬁxed r, θ , φ.FromEq.(11.71) we conclude that it occurs at

:= r

ergosphere

= M +

√

− a

cos

θ). (11.80)

Inside this radius, since g

> 0, all particles and photons must rotate with the hole.

Again, this effect can occur in other situations. Models for certain rotating stars are

known where there are toroidal regions of space in which g

> 0 (Butterworth and Ipser

1976). These will have these super-strong frame-dragging effects. They are called ergore-

gions, and their boundaries are ergotoroids. They can exist in solutions which have no

horizon at all. But the stars are extremely compact (relativistic) and very rapidly rotating.

It seems unlikely that real neutron stars would have ergoregions.

The Kerr horizon

In the Schwarzschild solution, the horizon was the place where g

= 0 and g

=∞.In

the Kerr solution, the ergosphere occurs at g

= 0 and the horizon is at g

=∞, i.e. where

 = 0:

:= r

horizon

= M +

√

− a

). (11.81)

It is clear that the Kerr ergosphere lies outside the horizon except at the poles, where it is

tangent to it. The full proof that this is the horizon is beyond our scope here: we need to

verify that no null lines can escape from inside r

. We shall simply take it as given (see

the next section below for a partial justiﬁcation). Since the area of the horizon is important

(Hawking’s area theorem), we shall calculate it.

The horizon is a surface of constant r and t,byEq.(11.81) and the fact that the metric

is stationary. Any surface of constant r and t has an intrinsic metric whose line element

comes from Eq. (11.71) with dt = dr = 0:

+ a

)

− a



sin

θ dφ

+ ρ

dθ

. (11.82)

The proper area of this surface is given by integrating the square root of the determinant of

this metric over all θ and φ:

A(r) =

2π

dφ

dθ

√

[(r

+ a

)

− a

]sinθ. (11.83)