Schutz B. A first course in general relativity

Подождите немного. Документ загружается.

283 11.1 Trajectories in the Schwarzschild spacetime

Conserved quantities

We begin our study of relativistic black holes by examining the trajectories of particles.

This will allow us eventually to see whether light rays are trapped or can escape.

We have seen (Eq. (7.29) and associated discussion) that when a spacetime has a certain

symmetry, then there is an associated conserved momentum component for trajectories.

Because our space has so many symmetries – time independence and spherical symmetry –

the values of the conserved quantities turn out to determine the trajectory completely. We

shall treat ‘particles’ with mass and ‘photons’ without mass in parallel.

Time independence of the metric means that the energy −p

is constant on the trajectory.

For massive particles with rest mass m = 0, we deﬁne the energy per unit mass (speciﬁc

energy)

E, while for photons we use a similar notation just for the energy E:

particle :

E :=−p

/m; photon : E =−p

. (11.5)

Independence of the metric of the angle φ about the axis implies that the angular momen-

tum p

is constant. We again deﬁne the speciﬁc angular momentum

L for massive particles

and the ordinary angular momentum L for photons:

particle

L := p

/m; photon L = p

. (11.6)

Because of spherical symmetry, motion is always conﬁned to a single plane, and we can

choose that plane to be the equatorial plane. Then θ is constant (θ = π/2) for the orbit, so

dθ/dλ = 0, where λ is any parameter on the orbit. But p

is proportional to this, so it also

vanishes. The other components of momentum are:

particle : p

= g

= m



1 −



−1

= m dr/dτ ,

= g

φφ

= m

L; (11.7)

photon : p



1 −



−1

= dr/dλ,

= dφ/dλ = L/r

. (11.8)

The equation for a photon’s p

should be regarded as deﬁning the afﬁne parameter λ.The

equation p ·p =−m

implies

particle :

− m



1 −



−1

+ m



1 −



−1



dτ



=−m

; (11.9)

284 Schwarzschild geometry and black holes

photon :

− E



1 −



−1



1 −



−1



dλ



= 0.

(11.10)

These can be solved to give the basic equations for orbits,

particle :



dτ



−



1 −





1 +



; (11.11)

photon :



dλ



= E

−



1 −



. (11.12)

Typesoforbits

Both equations have the same general form, and we deﬁne the effective potentials

particle :

(r) =



1 −





1 +



; (11.13)

photon : V

(r) =



1 −



. (11.14)

Their typical forms are plotted in Figs. 11.1 and 11.2, in which various points have been

labeled and possible trajectories drawn (dotted lines).

Both Eq. (11.11) and Eq. (11.12) imply that, since the left side is positive or zero, the

energy of a trajectory must not be less than the potential V. (Here and until Eq. (11.17)

we will take E and V to refer to

E and

V as well, since the remarks for the two cases are

∼

(r)

∼

Figure 11.1

Typical effective potential for a massive particle of ﬁxed speciﬁc angular momentum in the

Schwarzschild metric.

285 11.1 Trajectories in the Schwarzschild spacetime

(r)

Figure 11.2

The same as Fig. 11.1 for a massless particle.

identical.) So for an orbit of given E, the radial range is restricted to those radii for which

V is smaller than E. For instance, consider the trajectory which has the value of E indicated

by point G (in either diagram). If it comes in from r =∞, then it cannot reach smaller r

than where the dotted line hits the V

curve, at point G. Point G is called a turning point.

At G, since E

= V

we must have (dr/dλ)

= 0, from Eq. (11.12). Similar conclusions

apply to Eq. (11.11). To see what happens here we differentiate Eqs. (11.11) and (11.12).

For particles, differentiating the equation



dτ



−

(r)

with respect to τ gives



dτ



dτ



=−

(r)

dτ

particles :

dτ

=−

(r). (11.15)

Similarly, the photon equation gives

photons :

dλ

=−

(r). (11.16)

These are the analogs in relativity of the equation

ma =−∇φ,

where φ is the potential for some force. If we now look again at point G, we see that the

radial acceleration of the trajectory is outwards, so that the particle (or photon) comes in

to the minimum radius, but is accelerated outward as it turns around, and so it returns to

r =∞. This is a ‘hyperbolic’ orbit – the analog of the orbits which are true hyperbolae in

Newtonian gravity.

286 Schwarzschild geometry and black holes

It is clear from Eq. (11.15)or(Eq.(11.16) that a circular orbit (r = const.) is possible

only at a minimum or maximum of V

. These occur at points A and B in the diagrams (there

is no point B for photons). A maximum is, however, unstable, since any small change in

r results in an acceleration away from the maximum, by Eqs. (11.15) and (11.16). So for

particles, there is one stable (B) and one unstable circular orbit (A) for this value of

L.For

photons, there is only one unstable orbit for this L. We can be quantitative by evaluating

0 =



1 −





1 +

&

and

0 =

$

1 −



These give, respectively

particles : r =

1 ±



1 −

12M



1/2

; (11.17)

photons : r = 3M. (11.18)

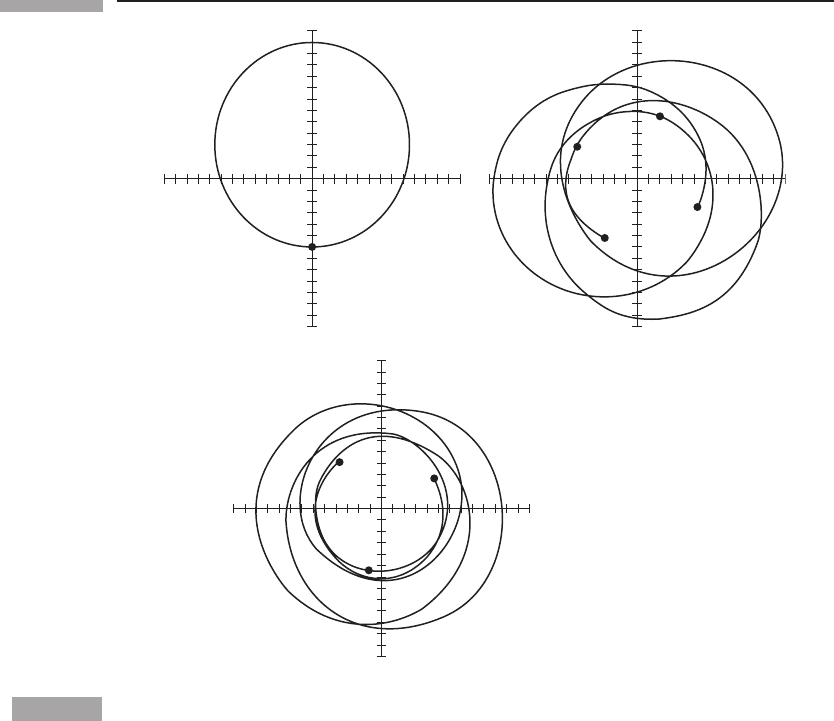
For particles, there are two radii, as we expect, but only if

> 12M

. The two radii are

identical for

= 12M

and don’t exist at all for

< 12M

. This indicates a qualitative

change in the shape of the curve for

(r) for small

L. The two cases,

= 12M

and

< 12M

, are illustrated in Fig. 11.3. Since there is a minimum

for a circular particle

orbit, there is also a minimum r, obtained by taking

= 12M

in Eq. (11.17)

particle : r

MIN

= 6M. (11.19)

For photons, the unstable circular orbit is always at the same radius, r = 3M, regard-

less of L.

The last kind of orbit we need consider is the one whose energy is given by the line

which passes through the point F in Figs. 11.1 and 11.2. Since this nowhere intersects the

potential curve, this orbit plunges right through r = 2M and never returns. From Exer. 1,

(a)

Point of

inflection

(r)

12M

(b)

(r)

12M

Figure 11.3

As Fig. 11.1 for the indicated values of speciﬁc angular momentum.

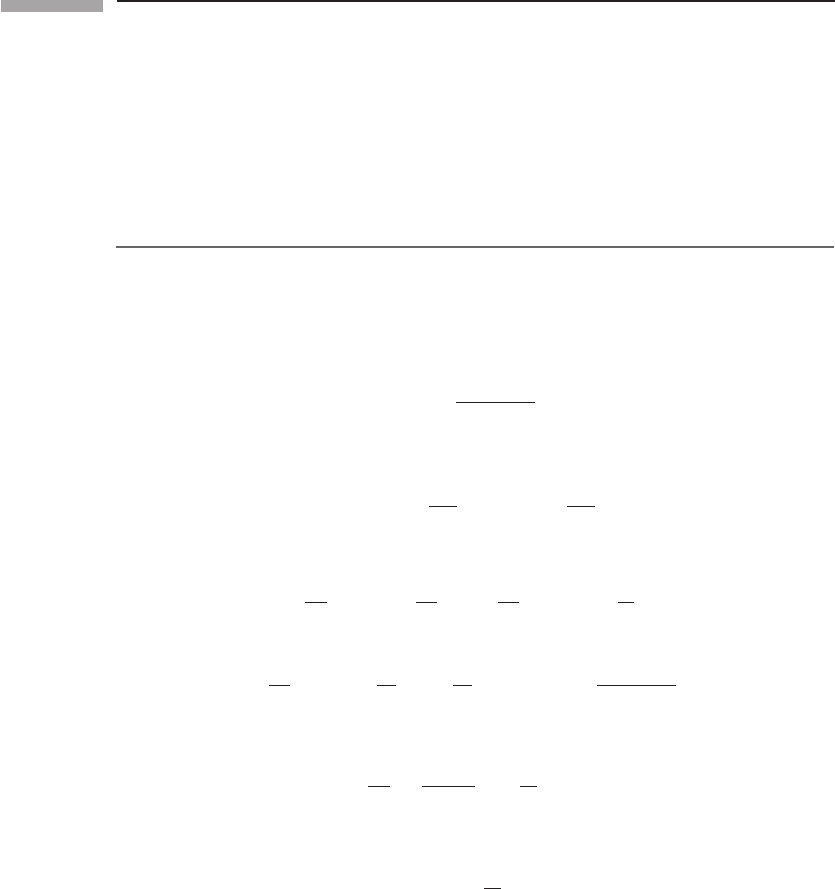
287 11.1 Trajectories in the Schwarzschild spacetime

§ 11.7, we see that for such an orbit the impact parameter (b) is small: it is aimed more

directly at the hole than are orbits of smaller

E and ﬁxed

Of course, if the geometry under consideration is a star, its radius R will exceed 2M, and

the potential diagrams, Figs. 11.1–11.3, will be valid only outside R. If a particle reaches

R, it will hit the star. Depending on R/M, then, only certain kinds of orbits will be possible.

Perihelion shift

A particle (or planet) in a (stable) circular orbit around a star will make one complete

orbit and come back to the same point (i.e. same value of φ) in a ﬁxed amount of coordi-

nate times, which is called its period P. This period can be determined as follows. From

Eq. (11.17) it follows that a stable circular orbit at radius r has angular momentum

1 − 3M/r

, (11.20)

and since

for a circular orbit, it also has energy



1 −





1 −



. (11.21)

Now, we have

dφ

dτ

:= U

= g

φφ

= g

φφ

L =

L (11.22)

and

dτ

:= U

= g

(−

E) =

1 − 2M/r

. (11.23)

We obtain the angular velocity by dividing these:

dφ

dt/dτ

dφ/dτ





1/2

. (11.24)

The period, which is the time taken for φ to change by 2π,is

P = 2π





1/2

. (11.25)

This is the coordinate time, of course, not the particle’s proper time. (But see Exer. 7,

§ 11.7: coordinate time is proper time far away.) It happens, coincidentally, that this is

identical to the Newtonian expression.

Now, a slightly noncircular orbit will oscillate in and out about a central radius r.In

Newtonian gravity the orbit is a perfect ellipse, which means, among other things, that

it is closed: after a ﬁxed amount of time it returns to the same point (same r and φ). In

GR, this does not happen and a typical orbit is shown in Fig. 11.4. However, when the

effects of relativity are small and the orbit is nearly circular, the relativistic orbit must be

almost closed: it must look like an ellipse which slowly rotates about the center. One way

to describe this is to look at the perihelion of the orbit, the point of closest approach to

288 Schwarzschild geometry and black holes

(a)

(c)

(b)

Figure 11.4

(a) A Newtonian orbit is a closed ellipse. Grid marked in units of M. (b) An orbit in the

Schwarzschild metric with pericentric and apcentric distances similar to those in (a). Pericenters

(heavy dots) advance by about 97

◦

per orbit. (c) A moderately more compact orbit than in (b) has

a considerably larger pericenter shift, about 130

◦

the star. (‘Peri’ means closest and ‘helion’ refers to the Sun; for orbits about any old star

the name ‘periastron’ is more appropriate. For orbits around Earth – ‘geo’ – we speak of

the ‘perigee’. These opposite of ‘peri’ is ‘ap’: the furthest distance. Thus, an orbit also

has an aphelion, apastron, or apogee, depending on what it is orbiting around. The general

terms, not speciﬁc to any particular object, are perapsis and apapsis.) The perihelion will

rotate around the star in some manner, and observers can hope to measure this. It has been

measured for Mercury to be 43



/century, and we must try to calculate it. Note that all other

planets are further from the Sun and therefore under the inﬂuence of signiﬁcantly smaller

relativistic corrections to Newtonian gravity. The measurement of Mercury’s precession

is a herculean task, ﬁrst accomplished in the 1800s. Due to various other effects, such as

the perturbations of Mercury’s orbit due to the other planets, the observed precession is

about 5600



/century. The 43



is only the part not explainable by Newtonian gravity, and

Einstein’s demonstration that his theory predicts exactly that amount was the ﬁrst evidence

in favor of the theory.

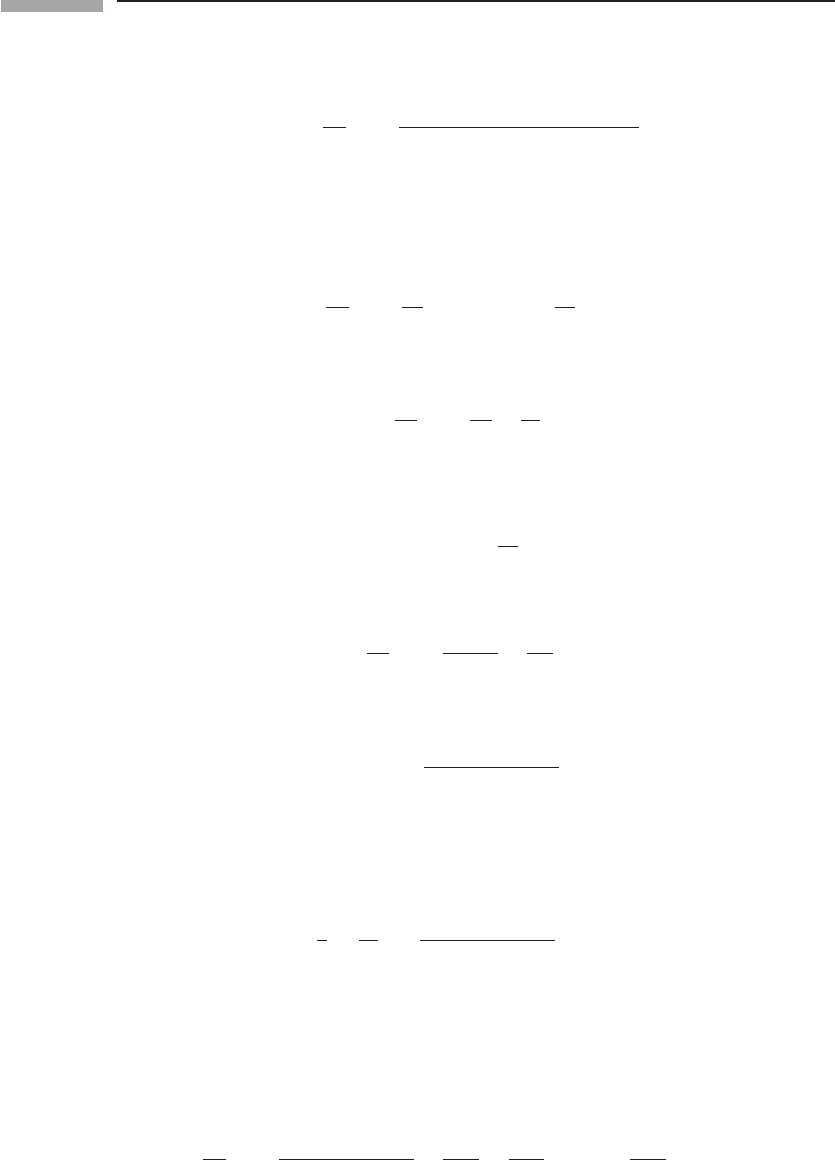
289 11.1 Trajectories in the Schwarzschild spacetime

To calculate the precession, let us begin by getting an equation for the particle’s orbit.

We have dr/dτ from Eq. (11.11). We get dφ/dτ from Eq. (11.22) and divide to get



dφ



−

(

1 − 2M/r

)



1 +



. (11.26)

It is convenient to deﬁne

u := 1/r (11.27)

and obtain



dφ



− (1 − 2Mu)



+ u



. (11.28)

The Newtonian orbit is found by neglecting u

terms (see Exer. 11, § 11.7)

Newtonian :



dφ



−

(1 − 2Mu) −u

. (11.29)

A circular orbit in Newtonian theory has u = M/

(take the square root equal to 1 in

Eq. (11.17)), so we deﬁne

y = u −

, (11.30)

so that y represents the deviation from circularity. We then get



dφ



− 1

− y

. (11.31)

It is easy to see that this is satisﬁed by

Newtonian : y =

+ M

− 1

1/2

cos(φ + B), (11.32)

where B is arbitrary. This is clearly periodic: as φ advances by 2π, y returns to its value

and, therefore, so does r. The constant B just determines the initial orientation of the orbit.

It is interesting, but unimportant for our purposes, that by solving for r we get

Newtonian :

+ M

− 1

1/2

cos(φ + B), (11.33)

which is the equation of an ellipse.

We now consider the relativistic case and make the same deﬁnition of y, but instead of

throwing away the u

term in Eq. (11.28) we assume that the orbit is nearly circular, so

that y is small, and we neglect only the terms in y

. Then we get

Nearly circular:



dφ



+ M

− 1

y −



1 −



. (11.34)

290 Schwarzschild geometry and black holes

This can be made analogous to Eq. (11.31) by completing the square on the right-hand

side. The result is the solution

y = y

+ A cos(kφ +B), (11.35)

where B is arbitrary and the other constants are

k =



1 −



1/2

= 3M

A =

+ M

− 1

− y

1/2

. (11.36)

The appearance of the constant y

just means that the orbit oscillates not about y = 0

(u =

M/L

) but about y = y

:Eq.(11.30) doesn’t use the correct radius for a circular orbit

in GR. The amplitude A is also somewhat different, but what is most interesting here is

the fact that k is not 1. The orbit returns to the same r when kφ goes through 2π ,from

Eq. (11.35). Therefore the change in φ from one perihelion to the next is

φ =

2π

= 2π



1 −



−1/2

, (11.37)

which, for nearly Newtonian orbits, is

φ  2π



1 +



. (11.38)

The perihelion advance, then, from one orbit to the next, is

φ = 6π M

radians per orbit. (11.39)

We can use Eq. (11.20) to obtain

L in terms of r, since the corrections for noncircu-

larity will make changes in Eq. (11.39) of the same order as terms we have already

neglected. Moreover, if we consider orbits about a nonrelativistic star, we can approximate

Eq. (11.20)by

1 − 3M/r

≈ Mr,

so that we get

φ ≈ 6π

. (11.40)

For Mercury’s orbit, r = 5.55 × 10

km and M = 1 M

= 1.47 km, so that

(φ)

Mercury

= 4.99 × 10

−7

radians per orbit. (11.41)

Each orbit take 0.24 yr, so the shift is

(φ)

Mercury

= .43



/yr = 43



/century. (11.42)

291 11.1 Trajectories in the Schwarzschild spacetime

Binary pulsars

Another system in which the pericenter shift is observable is the Hulse-Taylor binary pulsar

system PSR B1913+16 that we introduced in § 9.3. While this is not a “test particle”

orbiting a spherical star, but is rather two roughly equal-mass stars orbiting their common

center of mass, the pericenter shift (in this case, the periastron shift) still happens in the

same way. The two neutron stars of the Hulse-Taylor system have mean separation 1.2 ×

m, so using Eq. (11.40) with M = 1.4 M

= 2.07 km gives a crude estimate of φ =

3.3 × 10

−5

radians per orbit = 2

◦

.1 per year. This is much easier to measure than Mercury’s

shift! In fact, a more careful calculation, taking into account the high eccentricity of the

orbit and the fact that the two stars are of comparable mass, predict 4

◦

.2 per year.

For our purposes here we have calculated the periastron shift from the known masses

of the star. But in fact the observed shift of 4.2261

◦

± 0.0007 per year is one of the data

which enable us to calculate the masses of the neutron stars in the PSR B1913+16 sys-

tem. The other datum is another relativistic effect: a redshift of the signal which results

from two effects. One is the special-relativistic ‘transverse-Doppler’ term: the 0(v)

term

in Eq. (2.39). The other is the changing gravitational redshift as the pulsar’s eccentric orbit

brings it in and out of its companion’s gravitational potential. These two effects are obser-

vationally indistinguishable from one another, but their combined resultant redshift gives

one more number which depends on the masses of the stars. Using it and the periastron shift

and the Newtonian mass function for the orbit allows us to determine the stars’ masses and

the orbit’s inclination (see Stairs 2003).

While PSR B1913+16 was the ﬁrst binary pulsar to be discovered, astronomers now

know of many more (Lorimer 2008, Stairs 2003). The most dramatic system is the so-called

double pulsar system PSR J0737-3039, the ﬁrst binary discovered in which both members

are seen as radio pulsars (Kramer et al. 2006). In this system the pericenter shift is around

◦

per year! Because both pulsars can be tracked, this system promises to become the

best testing ground so far for the deviations of general relativity from simple Newtonian

behavior. We discuss some of these now.

Post-Newtonian gravity

The pericenter shift is an example of corrections that general relativity makes to Newto-

nian orbital dynamics. In going from Eq. (11.37)toEq.(11.38), we made an approximation

that the orbit was ‘nearly Newtonian’, and we did a Taylor expansion in the small quantity

, which by Eq. (11.20)is(M/r)(1 −3M/r). This is indeed small if the particle’s

orbit is far from the black hole, r  M. So orbits far from the hole are very nearly like

Newtonian orbits, with small corrections like the pericenter shift. These are orbits where,

in Newtonian language, the gravitational potential M/r is small, as is the particle’s orbital

velocity, which for a circular orbit is related to the potential by v

= M/r. Far from even

an extremely relativistic source, gravity is close to being Newtonian. We say that the peri-

center shift is a post-Newtonian effect, a correction to Newtonian motion in the limit of

weak ﬁelds and slow motion.

292 Schwarzschild geometry and black holes

We showed in § (8.4) that Newton’s ﬁeld equations emerge from the full equations of

general relativity in this same limit, where the ﬁeld (we called it h in that calculation) is

weak and the velocities small. It is possible to follow that approximation to higher order, to

keep the ﬁrst post-Newtonian corrections to the Einstein ﬁeld equations in this same limit.

If we did this, we would be able to show the result we have asserted, that the pericenter

shift is a general feature of orbital motion. We showed in that section that the metric of

spacetime that describes a Newtonian system with gravitational potential φ is,toﬁrstorder

in φ, given by the metric

=−(1 +2φ)dt

+ (1 − 2φ)(dx

+ dy

+ dz

). (11.43)

For comparison, let us take the limit for weak ﬁelds of the Schwarzschild metric given in

Eq. (11.1:

≈−



1 −





1 +



+ r

d

, (11.44)

where we have expanded g

and kept only the lowest order term in M/r. These two metrics

look similar – their g

terms are identical – but they appear not to be identical, because if

we transform the spatial line element of Eq. (11.43) to polar coordinates in the usual way,

we would expect to see in Eq. (11.44) the spatial line element

d



1 +



+ r

d

. (11.45)

(Readers who want to be reminded about the transformation from Cartesian to spherical

coordinates in ﬂat space should see Eq. (6.19) and Exer. 28, § 6.9.) Is this difference from

the spatial part of Eq. (11.44) an indication that the Schwarzschild metric does not obey

the Newtonian limit? The answer is no – we are dealing with a coordinate effect.

Coordinates in which the line element has the form of Eq. (11.45) are called isotropic

coordinates because there is no distinction in the metric among the directions x, y, and z.

Isotropic coordinates are related to Schwarzschild coordinates by a change in the deﬁnition

of the radial coordinate. If we call the isotropic coordinates (t, ¯r, θ , φ), where (t, θ, φ)are

the same as in Schwarzschild, then we make the simple transformation for large r given by

¯r = r − M. (11.46)

Then to lowest order in M/r or M/¯r, the expression 1 +2M/r in Eq. (11.44) equals 1 −

2M/¯r. But the factor in front of d

is r

, which becomes (again to ﬁrst order) ¯r

(1 +

2M/r). It follows that this simple transformation changes the spatial part of the line element

of Eq. (11.44)toEq.(11.45) in terms of the radial coordinate ¯r. This demonstrates that the

far ﬁeld of the Schwarzschild solution does indeed conform to the form in Eq. (8.50).

There are of course many other post-Newtonian effects in general relativity besides the

pericenter shift. In the next paragraph we will explore the deﬂection of light. Later in

this chapter we will meet the dragging of inertial frames due to the rotation of the source

of gravity (also called gravitomagnetism). It is possible to expand the Einstein equations

beyond the ﬁrst post-Newtonian equations and ﬁnd second and higher post-Newtonian

effects. Physicists have put considerable work into doing such expansions, because they