Schutz B. A first course in general relativity

Подождите немного. Документ загружается.

253 9.7 Exercises

31 Calculate the quadrupole tensor I

and its traceless counterpart I

–

(Eq. (9.87)) for the

following mass distributions.

(a) A spherical star where density is ρ(r, t). Take the origin of the coordinates in

Eq. (9.82) to be the center of the star.

(b) The star in (a), but with the origin of the coordinates at an arbitrary point.

x, y, and z axes respectively. Take the origin to be at the center of the ellipsoid.

(d) The ellipsoid in (c), but rotating about the z axis with angular velocity ω.

(e) Four masses m located respectively at the points (a,0,0),(0,a,0), (−a,0,0),

(0, −a,0).

(f) The masses as in (e), but all moving counter-clockwise about the z axis on a circle

of radius a with angular velocity ω.

(g) Two masses m connected by a massless spring, each oscillating on the x axis with

angular frequency ω and amplitude A about mean equilibrium positions a distance

apart, keeping their center of mass ﬁxed.

(h) Unequal masses m and M connected by a spring of spring constant k and equilib-

rium length l

, oscillating (with their center of mass ﬁxed) at the natural frequency

of the system, with amplitude 2A (this is the total stretching of the spring). Their

separation is along the x axis.

32 This exercise develops the TT gauge for spherical waves.

(a) In order to transform Eq. (9.83) to the TT gauge, use a gauge transformation gen-

erated by a vector ξ

= B

i(r−t)

/r, where B

is a slowly varying function of

. Find the general transformation law to order 1/r.

(b) Demand that the new

αβ

satisfy three conditions to order 1/r:

0μ

= 0,

and

μj

= 0, where n

:= x

/r is the unit vector in the radial direction. Show that

it is possible to ﬁnd functions B

, which accomplish such a transformation and

which satisfy  ξ

= 0 to order 1/r.

(d) By expanding R in Eq. (9.103) but discarding r

−1

terms, show that the higher-order

parts of

0μ

that are not eliminated by Eq. (9.104) are gauge terms to order v

, i.e.

up to second time derivatives in the expansion of

and ﬁrst time derivatives in

in Eq. (9.103).

33 (a) Let n

be a unit vector in three-dimensional Euclidean space. Show that P

= δ

−

is the projection tensor orthogonal to n

, i.e. show that for any vector V

,(i)

is orthogonal to n

, and (ii) P

= P

(b) Show that the TT gauge

of Eqs. (9.84)–(9.86) is related to the original

Eq. (9.83)by

= P

−

), (9.163)

where n

points in the z direction.

34 Show that I

–

is trace free, i.e. I

–

= 0.

35 For the systems described in Exer. 31, calculate the transverse-traceless quadrupole

radiation ﬁeld, Eqs. (9.85)–(9.86)or(9.163), along the x, y, and z axes. In Eqs. (9.85)–

(9.86) be sure to change the indices appropriately when doing the calculation on the x

and y axes, as in the discussion leading to Eq. (9.91).

254 Gravitational radiation

36 Use Eq. (9.163) or a rotation of the axes in Eqs. (9.85)–(9.86) to calculate the amplitude

and orientation of the polarization ellipse of the radiation from the simple oscillator,

Eq. (9.88), traveling at an angle θ to the x axis.

37 The ω and 2ω terms in Eq. (9.93) are qualitatively different, in that the 2ω term depends

only on the amplitude of oscillator A, while the ω term depends on both A and the

separation of the masses l

. Why should l

be involved – the masses don’t move over

that distance? The answer is that stresses are transmitted over that distance by the

spring, and stresses cause the radiation. To see this, do an analogous calculation for

a similar system, in which stresses are not passed over large distances. Consider a

system consisting of two pairs of masses. Each pair has one particle of mass m and

another of mass M  m. The masses within each pair are connected by a short spring

whose natural frequency is ω. The pairs’ centers of mass are at rest relative to one

another. The springs oscillate with equal amplitude in such a way that each mass m

oscillates sinusoidally with amplitude A, and the centers of oscillation of the masses

are separated by l

 A. The masses oscillate out of phase. Use the calculation of

Exer. 31(h) to show that the radiation ﬁeld of the system is Eq. (9.93) without the ω

term. The difference between this system and that in Eq. (9.93) may be thought to be

the origin of the stresses to maintain the motion of the masses m.

38 Do the same as Exer. 36 for the binary system, Eqs. (9.98)–(9.99), but instead of ﬁnding

the orientation of the linear polarization, ﬁnd the orientation of the ellipse of elliptical

polarization.

39 Let two spherical stars of mass m and M be in elliptical orbit about one another in

the x −y plane. Let the orbit be characterized by its total energy E and its angular

momentum L.

(a) Use Newtonian gravity to calculate the equation of the orbits of both masses about

their center of mass. Express the orbital period P, minimum separation a, and

eccentricity e as functions of E and L.

(b) Calculate I

–

for this system.

your result reduces to Eqs. (9.98)–(9.99) when m = M and the orbits are circular.

40 Show from Eq. (9.101) that spherically symmetric motions produce no gravitational

radiation.

41 Derive Eq. (9.115)fromEq.(9.114) in the manner suggested in the text.

42 (a) Derive Eq. (9.116).

(b) Derive Eqs. (9.117) and (9.118) by superposing Eqs. (9.107) and (9.116) and

assuming R is small.

43 Show that if we deﬁne an averaged stress–energy tensor for the waves

αβ

=

μν,α

TTμν

,β

 /32π (9.164)

(where denotes an average over both one period of oscillation in time and one

wavelength of distance in all spatial directions), then the ﬂux F of Eq. (9.122)isthe

component T

for that wave. A more detailed argument shows that Eq. (9.164) can in

fact be regarded as the stress–energy tensor of any wave packet, provided the averages

255 9.7 Exercises

are deﬁned suitably. This is called the Isaacson stress–energy tensor. See Misner et al.

(1973) for details.

44 (a) Derive Eq. (9.125)fromEq.(9.123).

(b) Justify Eq. (9.127)fromEq.(9.125).

45 (a) Consider the integral in Eq. (9.128). We shall do it by the following method.

(i) Argue on grounds of symmetry that



sin θ dθ dφ must be proportional

to δ

. (ii) Evaluate the constant of proportionality by explicitly doing the case

j = k = z.

(b) Follow the same method for Eq. (9.129). In (i) argue that the integral can depend

only on δ

, and show that the given tensor is the only one constructed purely from

that has the symmetry of being unchanged when the values of any two of its

indices are exchanged.

46 Derive Eqs. (9.130) and (9.131), remembering Eq. (9.124) and the fact that I

–

symmetric.

47 (a) Recall that the angular momentum of a particle is p

. It follows that the angular

momentum ﬂux of a continuous system across a surface x

= const. is T

iφ

. Use this

and Exer. 43 to show that the total z component of angular momentum radiated by

a source of gravitational waves (which is the integral over a sphere of large radius

of T

rφ

in Eq. (9.164)) is

=−

(

...

−

...

). (9.165)

(b) Show that if

μν

depends on t and φ only as cos(t − mφ), then the ratio of the

total energy radiated to the total angular momentum radiated is /m.

48 Calculate Eq. (9.135).

49 For the arbitrary binary system of Exer. 39:

(a) Show that the average energy loss rate over one orbit is

dE/dt=−

(m + M)

(1 − e

)

7/2



1 +



(9.166)

and from the result of Exer. 47(a)

dL/dt=−

(m + M)

5/2

7/2

(1 − e

)

7/2



1 +



, (9.167)

where μ = mM/(m +M) is the reduced mass.

(b) Show that

da/dt=−

μ(m + M)

(1 − e

)

7/2



1 +



, (9.168)

de/dt=−

304

μ(m + M)

(1 − e

)

5/2



1 +

121

304



, (9.169)

dP/dt=−

192π

μ(m + M)

3/2

5/2

(1 − e

)

7/2



1 +



. (9.170)

(Do parts (b) and (c) even if you can’t do (a).) These were originally derived by Peters

(1964).

Spherical solutions for stars

10.1 C oo rd i na te s f or spherically symmetric

spacetimes

For our ﬁrst study of strong gravitational ﬁelds in GR, we will consider spherically sym-

metric systems. They are reasonably simple, yet physically very important, since very

many astrophysical objects appear to be nearly spherical. We begin by choosing the

coordinate system to reﬂect the assumed symmetry.

Flat space in spherical coordinates

By deﬁning the usual coordinates (r, θ , φ), the line element of Minkowski space can be

written

=−dt

+ dr

+ r

(dθ

+ sin

θ dφ

). (10.1)

Each surface of constant r and t is a sphere or, more precisely, a two-sphere–atwo-

dimensional spherical surface. Distances along curves conﬁned to such a sphere are given

by the above equation with dt = dr = 0:

= r

(dθ

+ sin

θ dφ

):= r

d

, (10.2)

which deﬁnes the symbol d

for the element of solid angle. We note that such a sphere

has circumference 2π r and area 4π r

, i.e. 2π times the square root of the coefﬁcient of

d

and 4π times the coefﬁcient of d

respectively. Conversely, any two-surface where

the line element is Eq. (10.2) with r

independent of θ and φ has the intrinsic geometry of

a two-sphere.

Two-spheres in a curved spacetime

The statement that a spacetime is spherically symmetric can now be made more precise: it

implies that every point of spacetime is on a two-surface which is a two-sphere, i.e. whose

line element is

= f (r



, t)(dθ

+ sin

θ dφ

), (10.3)

where f (r



, t) is an unknown function of the two other coordinates of our manifold r



and

t. The area of each sphere is 4π f (r



, t). We deﬁne the radial coordinate r of our spherical

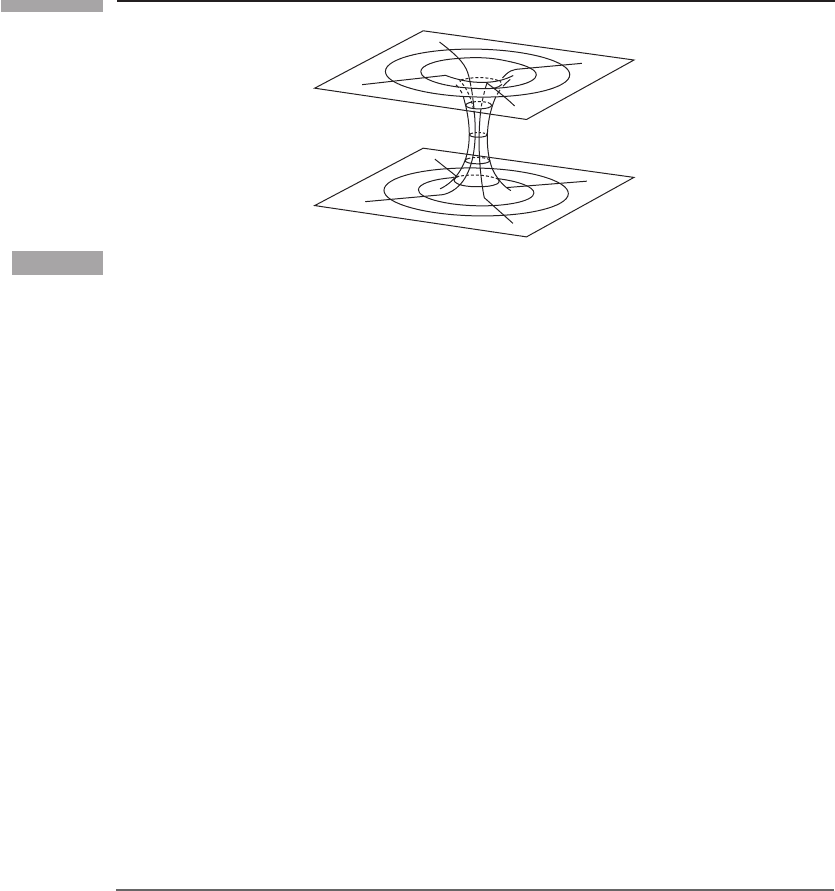
257 10.1 Coordinates for spherically symmetric spacetimes

Figure 10.1

Two plane sheets connected by a circular throat: there is circular (axial) symmetry, but the center

of any circle is not in the two-space.

geometry such that f (r



, t):= r

. This represents a coordinate transformation from (r



, t)

to (r, t). Then any surface r = const., t = const. is a two-sphere of area 4πr

and circum-

ference 2π r. This coordinate r is called the ‘curvature coordinate’ or ‘area coordinate’

because it deﬁnes the radius of curvature and area of the spheres. There is noapriorirela-

tion between r and the proper distance from the center of the sphere to its surface. This r

is deﬁned only by the properties of the spheres themselves. Since their ‘centers’ (at r = 0

in ﬂat space) are not points on the spheres themselves, the statement that a spacetime is

spherically symmetric does not require even that there be a point at the center. A simple

counter-example of a two-space in which there are circles but no point at the center of

them is in Fig. 10.1. The space consists of two sheets, which are joined by a ‘throat’. The

whole thing is symmetric about an axis along the middle of the throat, but the points on this

axis – which are the ‘centers’ of the circles – are not part of the two-dimensional surface

illustrated. Yet if φ is an angle about the axis, the line element on each circle is just r

dφ

where r is a constant labeling each circle. This r is the same sort of coordinate that we use

in our spherically symmetric spacetime.

Meshing the two-spheres into a three-space for t = const

Consider the spheres at r and r +d r. Each has a coordinate system (θ, φ),butuptonow

we have not required any relation between them. That is, we could conceive of having the

pole for the sphere at r in one orientation, while that for r + d r was in another. The sensible

thing is to say that a line of θ = const., φ = const. is orthogonal to the two-spheres. Such

a line has, by deﬁnition, a tangent e

. Since the vectors e

and e

lie in the spheres, we

require e

·e

=e

·e

= 0. This means g

rθ

= g

rφ

= 0 (recall Eqs. (3.3) and (3.21)). This

is a deﬁnition of the coordinates, allowed by spherical symmetry. We thus have restricted

themetrictotheform

= g

+ 2g

dr dt + 2g

0θ

dθ dt + 2g

0φ

dφ dt +g

+ r

d

. (10.4)

258 Spherical solutions for stars

Spherically symmetric spacetime

Since not only the spaces t = const. are spherically symmetric, but also the whole space-

time, we must have that a line r = const., θ = const., φ = const. is also orthogonal to the

two-spheres. Otherwise there would be a preferred direction in space. This means that e

orthogonal to e

and e

,org

tθ

= g

tφ

= 0. So now we have

= g

+ 2g

dr dt + g

+ r

d

. (10.5)

This is the general metric of a spherically symmetric spacetime, where g

, g

, and g

are functions of r and t. We have used our coordinate freedom to reduce it to the simplest

possible form.

10.2 Static spherically symmetric spacetimes

The metric

Clearly, the simplest physical situation we can describe is a quiescent star or black hole – a

static system. We deﬁne a static spacetime to be one in which we can ﬁnd a time coordinate

t with two properties: (i) all metric components are independent of t, and (ii) the geometry

is unchanged by time reversal, t →−t. The second condition means that a ﬁlm made of

the situation looks the same when run backwards. This is not logically implied by (i), as

the example of a rotating star makes clear: time reversal changes the sense of rotation, but

the metric components will be constant in time. (A spacetime with property (i) but not

necessarily (ii) is said to be stationary.)

Condition (ii) has the following implication. The coordinate transformation (t, r, θ , φ) →

(−t, r, θ, φ) has 

=−1, 

= δ

, and we ﬁnd

= (

)

= g

0¯r

= 



¯r

=−g

¯r¯r

= (

¯r

)

= g

⎫

⎬

⎭

(10.6)

Since the geometry must be unchanged (i.e. since g

¯α

= g

αβ

), we must have g

≡ 0. Thus,

the metric of a static, spherically symmetric spacetime is

=−e

2

+ e

2

+ r

d

, (10.7)

where we have introduced (r) and (r) in place of the two unknowns g

(r) and g

(r).

This replacement is acceptable provided g

< 0 and g

> 0 everywhere. We shall see

below that these conditions do hold inside stars, but they break down for black holes.

When we study black holes in the next chapter we shall have to look carefully again at our

coordinate system.

259 10.2 Static spherically symmetric spacetimes

If we are interested in stars, which are bounded systems, we are entitled to demand that,

far from the star, spacetime is essentially ﬂat. This means that we can impose the following

boundary conditions (or asymptotic regularity conditions) on Einstein’s equations:

lim

r→∞

(r) = lim

r→∞

(r) = 0. (10.8)

With this condition we say that spacetime is asymptotically ﬂat.

Physical interpretation of metric terms

Since we have constructed our coordinates to reﬂect the physical symmetries of the space-

time, the metric components have useful physical signiﬁcance. The proper radial distance

from any radius r

to another radius r



dr, (10.9)

since the curve is one on which dt = dθ = dφ = 0. More important is the signiﬁcance

of g

. Since the metric is independent of t, we know from Ch. 7 that any particle fol-

lowing a geodesic has constant momentum component p

, which we can deﬁne to be the

constant −E:

:=−E. (10.10)

But a local inertial observer at rest (momentarily) at any radius r of the spacetime mea-

sures a different energy. Her four-velocity must have U

= d x

/d τ = 0 (since she is

momentarily at rest), and the condition



U ·



U = 1 implies U

= e

−

. The energy she

measures is

∗

=−



U ·p = e

−

E. (10.11)

We therefore have found that a particle whose geodesic is characterized by the constant

E has energy e

−

E relative to a locally inertial observer at rest in the spacetime. Since

−

= 1 far away, we see that E is the energy a distant observer would measure if the

particle gets far away. We call it the energy at inﬁnity. Since e

−

> 1 everywhere else (this

will be clear later), we see that the particle has larger energy relative to inertial observers

that it passes elsewhere. This extra energy is just the kinetic energy it gains by falling in a

gravitational ﬁeld. The energy is studied in more detail in Exer. 3, § 10.9.

This is particularly signiﬁcant for photons. Consider a photon emitted at radius r

and

received very far away. If its frequency in the local inertial frame is ν

(which would be

determined by the process emitting it, e.g. a spectral line), then its local energy is hν

(h being Planck’s constant) and its conserved constant E is hν

exp [(r

)]. When it

reaches the distant observer it is measured to have energy E, and hence frequency E/h ≡

rec

= ν

exp [(r

)]. The redshift of the photon, deﬁned by

z =

rec

− λ

rec

− 1, (10.12)

260 Spherical solutions for stars

is therefore

z = e

−(r

)

− 1. (10.13)

This important equation attaches physical signiﬁcance to e



. (Compare this calculation

with the one in Ch. 2.)

The Einstein tensor

We can show that for the metric given by Eq. (10.7), the Einstein tensor has components

2

[r(1 −e

−2

)], (10.14)

=−

2

(1 − e

−2

) +





, (10.15)

θθ

= r

−2

[



+ (



)

+ 



/r −







− 



/r], (10.16)

φφ

= sin

θG

θθ

, (10.17)

where 



:= d/dr, etc. All other components vanish.

10.3 S t at ic p e rf ec t fl u id E i ns te i n e q ua t io n s

Stress–energy tensor

We are interested in static stars, in which the ﬂuid has no motion. The only nonzero

component of



U is therefore U

. What is more, the normalization condition



U ·



U =−1 (10.18)

implies, as we have seen before,

= e

−

, U

=−e



. (10.19)

Then T has components given by Eq. (4.38):

= ρ e

2

, (10.20)

= p e

2

, (10.21)

θθ

= r

p, (10.22)

φφ

= sin

θ T

θθ

. (10.23)

All other components vanish.

261 10.3 Static perfect fluid Einstein equations

Equation of state

The stress–energy tensor involves both p and ρ, but these may be related by an equation of

state. For a simple ﬂuid in local thermodynamic equilibrium, there always exists a relation

of the form

p = p(ρ, S), (10.24)

which gives the pressure p in terms of the energy density ρ and speciﬁc entropy S.Weoften

deal with situations in which the entropy can be considered to be a constant (in particular,

negligibly small), so that we have a relation

p = p(ρ). (10.25)

These relations will of course have different functional forms for different ﬂuids. We will

suppose that some such relation always exists.

Equations of motion

The conservation laws are (Eq. (7.6))

αβ

;β

= 0. (10.26)

These are four equations, one for each value of the free index α. Because of the symmetries,

only one of these does not vanish identically: the one for which α = r.Itimplies

(ρ +p)

d

=−

. (10.27)

This is the equation that tells us what pressure gradient is needed to keep the ﬂuid static in

the gravitational ﬁeld, the effect of which depends on d/dr.

Einstein equations

The (0, 0) component of Einstein’s equations can be found from Eqs. (10.14) and (10.20).

It is convenient at this point to replace (r) with a different unknown function m(r)

deﬁned as

m(r):=

r(1 −e

−2

), (10.28)

262 Spherical solutions for stars

= e

2



1 −

2m(r)



−1

. (10.29)

Then the (0,0) equation implies

dm(r)

= 4π r

ρ. (10.30)

This has the same form as the Newtonian equation, which calls m(r) the mass inside the

sphere of radius r. Therefore, in relativity we call m(r) the mass function, but it cannot be

interpreted as the mass energy inside r since total energy is not localizable in GR. We shall

explore the Newtonian analogy in § 10.5 below.

The (r, r) equation, from Eqs. (10.15) and (10.21), can be cast in the form

d

m(r) +4π r

r[r − 2m(r)]

. (10.31)

If we have an equation of state of the form Eq. (10.25), then Eqs. (10.25), (10.27), (10.30),

and (10.31) are four equations for the four unknowns , m, ρ, p. If the more general equa-

tion of state, Eq. (10.24), is needed, then S is a completely arbitrary function. There is no

additional information contributed by the (θ, θ ) and (φ, φ) Einstein equation, because (i) it

is clear from Eqs. (10.16), (10.17), (10.22), and (10.23) that the two equations are essen-

tially the same, and (ii) the Bianchi identities ensure that this equation is a consequence of

Eqs. (10.26), (10.30), and (10.31).

10.4 T h e ex te rio r g eo m et r y

Schwarzschild metric

In the region outside the star, we have ρ = p = 0, and we get the two equations

= 0, (10.32)

d

r(r − 2m)

. (10.33)