Schutz B. A first course in general relativity

Подождите немного. Документ загружается.

233 9.3 The generation of gravitational waves

So the wave amplitude is always less than, or of the order of, the Newtonian potential φ

Why then can we detect h but not φ

itself; why can we hope to ﬁnd waves from a super-

nova in a distant galaxy without being able to detect its presence gravitationally before the

explosion? The answer lies in the forces involved. The Newtonian tidal gravitational force

on a detector of size l

at a distance r is about φ

, while the wave force is hl

(see

Eq. (9.45)). The wave force is thus a factor φ

(ωr)

∼ (φ

r/R)

larger than the Newtonian

force. For a relativistic system (φ

∼ 0.1) of size 1 AU (∼ 10

m), observed by a detector

a distance 10

m away, this factor is 10

. This estimate, incidentally, gives the largest

distance r at which we may still approximate the gravitational ﬁeld of a dynamical system

as Newtonian (i.e. neglecting wave effects): r = R/φ

, where R is the size of the system.

TheestimateinEq.(9.100) is really an optimistic upper limit, because it assumed that

all the mass motions contributed to D

. In realistic situations this could be a serious over-

estimate because of the following fundamental fact: spherically symmetric motions do not

radiate. The rigorous proof of this is discussed in Ch. 10, but in Exer. 40, § 9.7 we derive it

from linearized theory, Eq. (9.101) below. It also seems to follow from Eq. (9.82a): if T

is spherically symmetric, then I

is proportional to δ

and I

–

vanishes. But this argu-

ment has to be treated with care, since Eq. (9.82a) is part of an approximation designed

to give only the dominant radiation. We would have to show that spherically symmetric

motions would not contribute to terms of higher order in the approximation if they were

present. This is in fact true, and it is interesting to ask what eliminates them. The answer

is Eq. (9.77): conservation of energy eliminates ‘monopole’ radiation in linearized theory,

just as conservation of charge eliminates monopole radiation in electromagnetism.

The danger of using Eq. (9.82a) too glibly is illustrated in Exer. 31e, § 9.7: four equal

masses at the corners of a rotating square give no time-dependent I

and hence no radiation

in this approximation. But they would emit radiation at a higher order of approximation.

Exact solution of the wave equation

Readers who have studied the wave equation, Eq. (9.64), will know that its outgoing-wave

solution for arbitrary T

μν

is given by the retarded integral

μν

(t, x

) = 4

μν

(t −R, y

)

y, (9.101)

R =|x

− y

where the integral is over the past light cone of the event (t, x

) at which

μν

is evaluated.

We let the origin be inside the source and we suppose that the ﬁeld point x

is far away,

| := r |y

| := y, (9.102)

and that time derivatives of T

μν

are small. Then, inside the integral, Eq. (9.101), the

dominant contribution comes from replacing R

−1

by r

−1

μν

(t, x

) ≈

μν

(t −R, y

y. (9.103)

234 Gravitational radiation

This is the generalization of Eq. (9.74). Now, by virtue of the conservation laws Eq. (9.77)

μν

,ν

= 0,

we have

0μ

y = const., (9.104)

i.e. the total energy and momentum are conserved. It follows that the 1/r part of

0μ

is time

independent to lowest order, so it will not contribute to any wave ﬁeld. This generalizes

Eq. (9.80). Again, see Exer. 32, § 9.7. Then, using Eq. (9.81), we get the generalization of

Eq. (9.83):

(t, x

) =−

jk,00

(t −r). (9.105)

As before, we can adopt the TT gauge to get

–

xx,00

(t −r) −I

–

yy,00

(t −r)],

–

xx,00

(t −r). (9.106)

9.4 The energy carried away by gravitational waves

Preview

We have seen that gravitational waves can put energy into things they pass through. This

is how bar detectors work. It stands to reason, then, that they also carry energy away from

their sources. This is a very important aspect of gravitational wave theory because, as we

shall see, there are some circumstances in which the effects of this loss of energy on a

source can be observed, even when the gravitational waves themselves cannot be detected.

There are a number of different methods of deriving the formula for this energy loss (see

Misner et al. 1973) and the problem has attracted a considerable amount of effort and has

been attacked from many different points of view; see Damour (1987), Schutz (1980a),

Futamase (1983), or Blanchet (2006). Our approach here will remain within the simple

case of linear theory and will make the maximum use of what we already know about the

waves.

In our discussion of the harmonic oscillator as a detector of waves in § 9.2, we implicitly

assumed that the detector was a kind of ‘test body’, where the inﬂuence on the gravitational

wave ﬁeld is negligible. But this is, strictly speaking, inconsistent. If the detector acquires

energy from the waves, then surely the waves must be weaker after passing through the

detector. That is, ‘downstream’ of the detector they should have slightly lower amplitude

than ‘upstream’. It is easy to see how this comes about once we realize that in § 9.2 we

ignored the fact that the oscillator, once set in motion by the waves, will radiate waves

itself. We solved this in § 9.3 and found, in Eq. (9.88), that waves of two frequencies will

be emitted. Consider the emitted waves with frequency , the same as the incident wave.

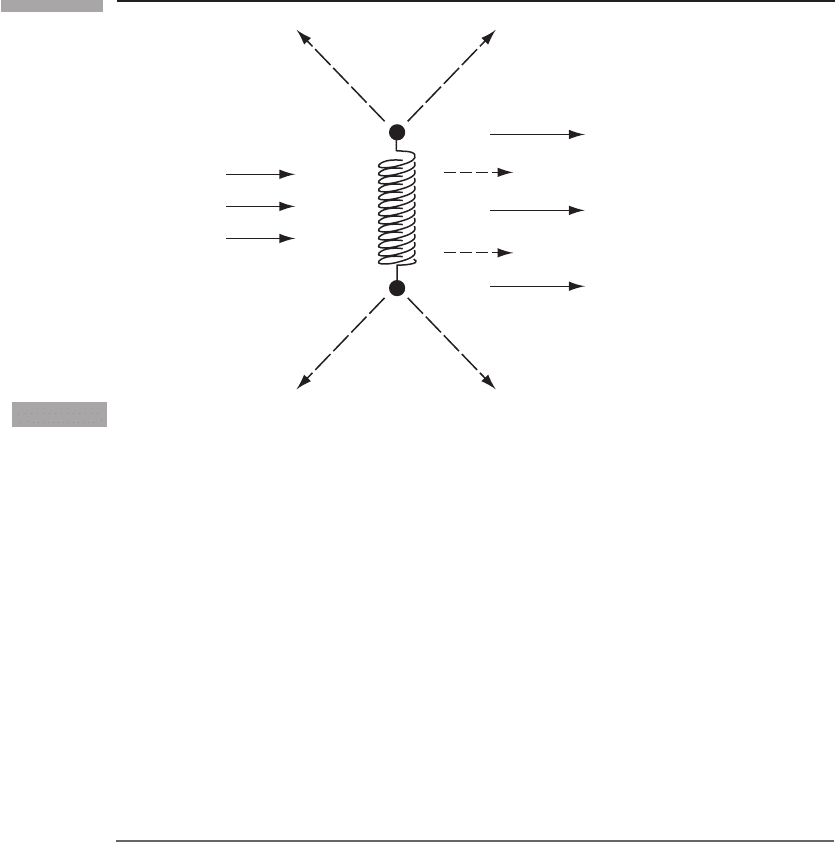
235 9.4 The energy carried away by gravitational waves

Radiated wave

Incident

Destructive interference

Downstream

Wave

Upstream

Figure 9.5

When the detector of Fig. 9.2 is excited by a wave, it re-radiates some waves itself.

The part that is emitted exactly downstream has the same frequency as the incident wave,

so the total downstream wave ﬁeld has an amplitude that is the sum of the two. We will

see below that the two interfere destructively, producing a net decrease in the downstream

amplitude (see Fig. 9.5). (In other directions, there is no net interference: the waves simply

pass through each other.) By assuming that this amplitude change signals a change in the

energy actually carried by the waves, and by equating this energy change to the energy

extracted from the waves by the detector, we will arrive at a simple expression for the

energy carried by the waves as a function of their amplitude. We will then be able to

calculate the energy lost by bodies that radiate arbitrarily, since we know from § 9.3 what

waves they produce.

The energy flux of a gravitational wave

What we are after is the energy ﬂux, the energy carried by a wave across a surface per unit

area per unit time. It is more convenient, therefore, to consider not just one oscillator but

an array of them ﬁlling the plane z = 0. We suppose they are very close together, so we

may regard them as a nearly continuous distribution of oscillators, σ oscillators per unit

area (Fig. 9.6). If the incident wave is, in the TT gauge,

= A cos (z −t),

=−

(9.107)

all other components vanishing, then in § 9.2 we have seen that each oscillator responds

with a steady oscillation (after transients have died out) of the form

ξ = R cos(t + φ), (9.108)

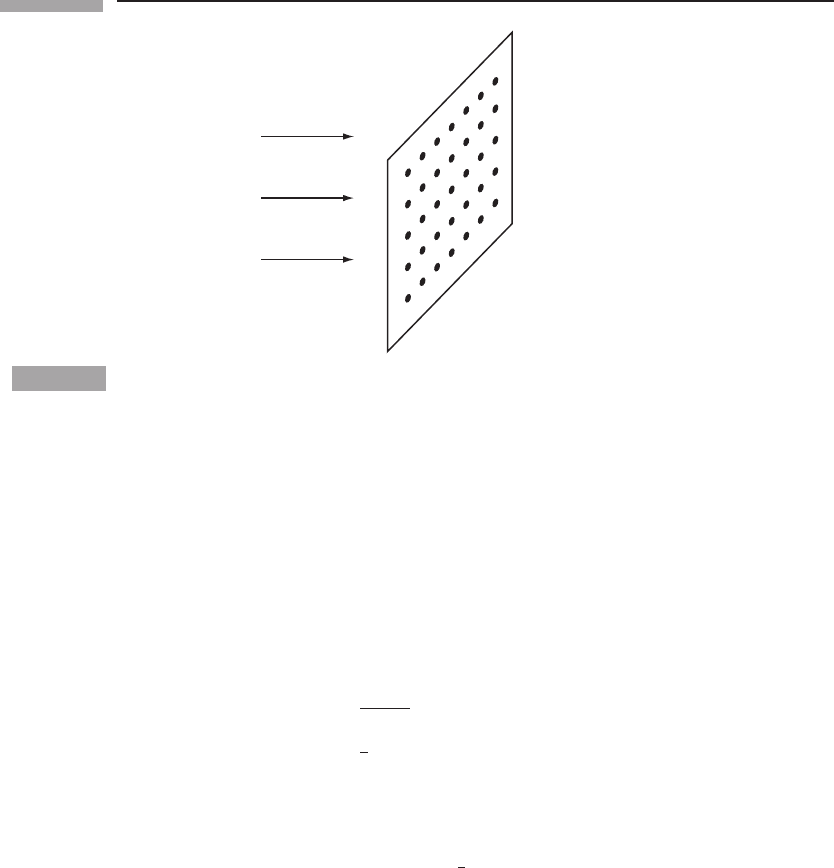
236 Gravitational radiation

Incident wave

σ Oscillators per unit area

Figure 9.6

The situation when detectors of Fig. 9.5 are arranged in a plane at a density of σ per unit area.

where R and φ are given by Eqs. (9.48) and (9.49) respectively. This motion is steady

because the energy dissipated by friction in the oscillators is compensated by the work

done on the spring by the tidal gravitational forces of the wave. It follows that the wave

supplies an energy to each oscillator at a rate equal to

d E/d t = ν (dξ/d t)

= mγ (dξ/d t)

. (9.109)

Averaging this over one period of oscillation, 2π/, in order to get a steady energy loss,

gives (angle brackets denote the average)

dE/dt=

2π/

mγ

sin

(t +φ)dt

mγ

. (9.110)

This is the energy supplied to each oscillator per unit time. With σ oscillators per unit area,

the net energy ﬂux F of the wave must decrease on passing through the z = 0 plane by

δF =−

σ mγ

. (9.111)

We calculate the change in the amplitude downstream independently of the calcula-

tionthatledtoEq.(9.111). Each oscillator has a quadrupole tensor given by Eq. (9.88),

with ωt replaced by t + φ and A replaced by R/2. (Each mass moves an amplitude A,

one-half of the total stretching of the spring R.) Since in our case R is tiny compared to

(R = 0(h

)), the 2 term in Eq. (9.88) is negligible compared to the  term. So each

oscillator has

= ml

R cos(t +φ). (9.112)

By Eq. (9.83), each oscillator produces a wave amplitude

=−2

R cos[(r −t) −φ]/r (9.113)

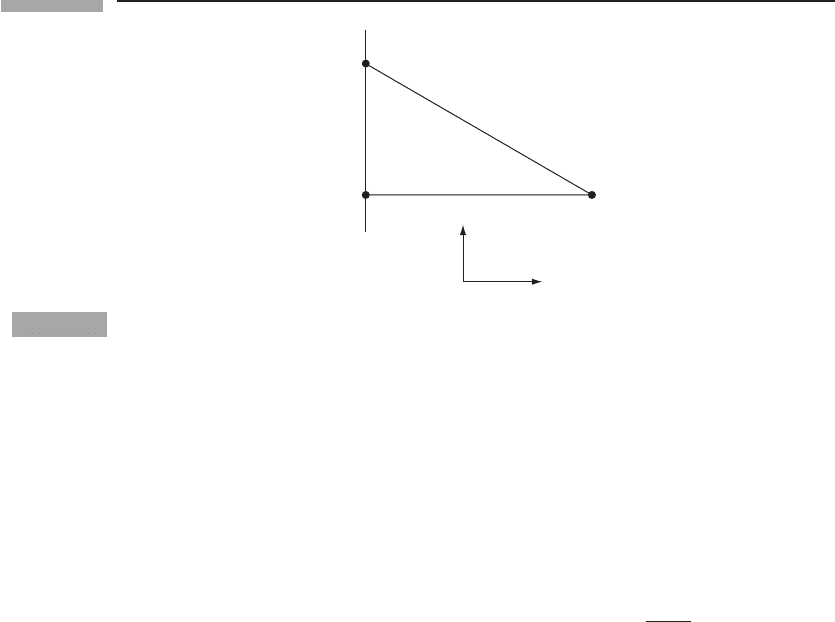
237 9.4 The energy carried away by gravitational waves



∼

Figure 9.7

Geometry for calculating the ﬁeld at P duetoanoscillatoratO.

at any point a distance r away. (We call it δ

to indicate that it is small compared to the

incident wave.) It is a simple matter to get the total radiated ﬁeld by adding up the contri-

butions due to all the oscillators. In Fig. 9.7, consider a point P a distance z downstream

from the plane of oscillators. Set up polar coordinates ( ˜ω, φ) in the plane, centered at Q

beneath P. A typical oscillator O at a distance ˜ω from Q contributes a ﬁeld, Eq. (9.113), at

P, with r = ( ˜ω

+ z

)

1/2

. Since the number of such oscillators between ˜ω and ˜ω +d ˜ω is

2πσ ˜ω d ˜ω, the total oscillator-produced ﬁeld at P is

total

=−2m

R2π

∞

σ cos[(r −t) −φ]

˜w d ˜w

But we may change the integration variable to r,

˜w d ˜w = r dr,

obtaining

total

=−2m

R2π

∞

σ cos[(r −t) −φ]dr. (9.114)

If σ were constant, this would be trivial to integrate, but its value would be undeﬁned at

r =∞. Physically, we should expect that the distant oscillators play no real role, so we

adopt the device of assuming that σ is proportional to exp (−εr) and allowing ε to tend to

zero after the integration. The result is

total

= 4πσml

R sin[(z − t) −φ]. (9.115)

So the plane of oscillators sends out a net plane wave. To compare this to the incident

wave, we must put Eq. (9.115) in the same TT gauge (recall that Eq. (9.83)isnot in the TT

gauge), with the result (Exer. 42, § 9.7)

=−δ

= 2πσml

R sin[(z − t) −φ]. (9.116)

238 Gravitational radiation

If we now add this to the incident wave, Eq. (9.107), we get the net result, to ﬁrst order

in R,

net

+ δ

= (A −2πσml

R sin φ) cos[(z −t) −ψ], (9.117)

where

tan ψ =

2πσml

cos φ. (9.118)

Apart from a small phase shift ψ, the net effect is a reduction in the amplitude A by

δA =−2πσml

R sin φ. (9.119)

This reduction must be responsible for the decrease in ﬂux F downstream. Dividing

Eq. (9.111)byEq.(9.119) and using Eqs. (9.48) and (9.49) to eliminate R and φ gives the

remarkably simple result

δF

δA

16π



A. (9.120)

This is our key result. It says that a change δA in the amplitude A of a wave of frequency

 changes its ﬂux F (averaged over one period) by an amount depending only on , A,

and δA. The oscillators helped us to derive this result from conservation of energy, but

they have dropped out completely! Eq. (9.120) is a property of the wave itself. We can

‘integrate’ Eq. (9.120) to get the total ﬂux of a wave of frequency  and amplitude A:

F =

32π



. (9.121)

Since the average of the square of the wave, Eq. (9.107), is

(

)

=

(again, angle brackets denote an average over one period), and since there are only two

nonvanishing components of

μν

, we can also write Eq. (9.121)as

F =

32π





μν

TTμν

.

(9.122)

This form is invariant under background Lorentz transformations, but not under gauge

changes. Since one polarization can be transformed into another by a background Lorentz

transformation (a rotation), Eq. (9.122) applies to all polarizations and hence to arbitrary

plane waves of frequency . In fact, since it gives an energy rate per unit area, it applies

to any wavefront, either plane waves or the spherical expanding ones of § 9.3: we can

always look at a small enough area that the curvature of the wavefront is not noticeable.

The generalization to arbitrary waves (no single frequency) is in Exer. 43, § 9.7.

The reader who remembers the discussion of energy in § 7.3 may object that this whole

derivation is suspect because of the difﬁculty of deﬁning energy in GR. Indeed, we have

not proved that energy is conserved, that the energy put into the oscillators must equal

the decrease in ﬂux; we have simply assumed this in order to derive the ﬂux. Our proof

239 9.4 The energy carried away by gravitational waves

may be turned around, however, to argue that the ﬂux we have constructed is the only

acceptable deﬁnition of energy for the waves, since our calculation shows it is conserved,

when added to other energies, to lowest order in h

μν

. The qualiﬁcation ‘to lowest order’

is important, since it is precisely because we are almost in ﬂat spacetime that, at lowest

order, we can construct conserved quantities. At higher order, away from linearized theory,

local energy cannot be so easily deﬁned, because the time dependence of the true metric

becomes important. These questions are among the most fundamental in relativity, and

are discussed in detail in any of the advanced texts. Our equations should be used only in

linearized theory.

Energy lost by a radiating system

Consider a general isolated system, radiating according to Eqs. (9.82)–(9.87). By integrat-

ing Eq. (9.122) over a sphere surrounding the system, we can calculate its net energy loss

rate. For example, at a distance r along the z axis, Eq. (9.122)is

F =



32πr

2(I

–

− I

–

)

+ 8I

–

. (9.123)

Use of the identity

–

= I

–

+ I

–

+ I

–

= 0 (9.124)

(which follows from Eq. (9.87)) gives, after some algebra,

F =



16πr

2I

–

− 4I

–

+ I

–

. (9.125)

Now, the index z appears here only because it is the direction from the center of the coor-

dinates, where the radiation comes from. It is the only part of F which depends on the

location on the sphere of radius r about the source, since all the components of I

–

depend

on time but not position. Therefore we can generalize Eq. (9.125) to arbitrary locations on

the sphere by using the unit vector normal to the sphere,

= x

/r. (9.126)

We get for F

F =



16πr

2I

–

− 4n

–

+ n

–

. (9.127)

The total luminosity of the source is the integral of this over the sphere of radius r.In

Exer. 45, § 9.7 we prove the following integrals over the entire sphere

sin θ dθ dφ =

4π

, (9.128)

sin θ dθ dφ =

4π

(δ

+ δ

). (9.129)

240 Gravitational radiation

It then follows that the luminosity L of a source of gravitational waves is

L =

sin θ dθ dφ =



2I

–

−

–

+ I

–

+ I

–

), (9.130)

L =



I

–

. (9.131)

The generalization to cases where I

–

has a more general time dependence is

L =



...

–

...

–

, (9.132)

where dots denote time derivatives.

It must be stressed that Eqs. (9.121) and (9.132) are acccurate only for weak gravita-

tional ﬁelds and slow velocities. They can at best give only order-of-magnitude results for

highly relativistic sources of gravitational waves. But in the spirit of our derivation and

discussion of the order-of-magnitude estimate of h

in Eq. (9.70), we can still learn some-

thing about strong sources from Eq. (9.121). Since I

is of order MR

,Eq.(9.121) tells us

that L ∼ M



∼ (M/R)

(R)

∼ φ

. The luminosity is a very sensitive function of

the velocity. The largest velocities we should expect are of the order of the velocity of free

fall, v

∼ φ

, so we should expect

L  (φ

)

. (9.133)

Since φ

 1, the luminosity in geometrized units should never substantially exceed one.

In ordinary units this is

L  1 = c

/G ≈ 3.6 ×10

W. (9.134)

We can understand why this particular luminosity is an upper limit by the following

simple argument. The radiation ﬁeld inside a source of size R and luminosity L has energy

density  L/R

(because |T

|∼|v

= cT

= T

), which is the ﬂux across its sur-

face. The total energy in radiation is therefore  LR. The Newtonian potential of the

radiation alone is therefore  L. We shall see in the next chapter that anything where

the Newtonian potential substantially exceeds one must form a black hole: its gravita-

tional ﬁeld will be so strong that no radiation will escape at all. Therefore L ∼ 1isthe

largest luminosity any source can have. This argument applies equally well to all forms of

radiation, electromagnetic as well as gravitational. The brightest quasars and gamma-ray

bursts, which are the most luminous classes of object so far observed, have a (geometrized)

luminosity  10

−10

. By contrast, black hole mergers (Ch. 11) have been shown by numer-

ical simulations to reach peak luminosities ∼ 10

−3

, all of the energy of course emitted in

gravitational waves.

An example. The Hulse–Taylor binary pulsar

In § 9.3 we calculated I

–

for a binary system consisting of two stars of equal mass M in

circular orbits a distance l

apart. If we use the real part of Eq. (9.97)inEq.(9.132), we get

241 9.4 The energy carried away by gravitational waves

L =

. (9.135)

Eliminating l

in favor of M and ω, we get

L =

√

(Mω)

10/3

≈ 4.0(Mω)

10/3

. (9.136)

This expression illustrates two things: ﬁrst, that L is dimensionless in geometrized units

and, second, that it is almost always easier to compute in geometrized units, and then

convert back at the end. The conversion is

L (SI units) =

L (geometrized)

= 3.63 × 10

−1

× L (geometrized). (9.137)

So for the binary pulsar system described in § 9.3, if its orbit were circular, we would have

ω = 2π/P = 7.5049 ×10

−13

−1

and

L = 1.71 ×10

−29

(9.138)

in geometrized units. We can, of course, convert this to watts, but a more meaningful pro-

cedure is to compare this with the Newtonian energy of the system, which is (deﬁning the

orbital radius r =

E =

Mω

−

(ω

−

M) =−

=−4

−2/3

5/3

2/3

≈−0.40M

5/3

2/3

(9.139)

=−1.11 ×10

−3

m. (9.140)

The physical question is: How long does it take to change this? Put differently, the energy

radiated in waves must change the orbit by decreasing its energy, which makes |E| larger

and hence ω larger and the period smaller. What change in the period do we expect in, say,

one year?

From Eq. (9.139), by taking logarithms and differentiating, we get

dω

=−

. (9.141)

Since dE/dt is just −L, we can solve for dP/dt:

dP/dt = (3 PL)/(2E) ≈−15 PM

−1

(M)

8/3

=−2.0 ×10

−13

, (9.142)

which is dimensionless in any system of units. It can be reexpressed in seconds per year:

dP/dt =−6.0 ×10

−6

syr

. (9.143)

242 Gravitational radiation

This estimate needs to be revised to allow for the eccentricity of the orbit, which is con-

siderable: e = 0.617. The correct formula is derived in Exer. 49, § 9.7. The result is that

the true rate of energy loss is some 12 times our estimate, Eq. (9.138). This is such a large

factor because the stars’ maximum angular velocity (when they are closest) is larger than

the mean value we have used for , and since L depends on the angular velocity to a high

power, a small change in the angular velocity accounts for this rather large factor of 12. So

the relativistic prediction is:

dP/dt =−2.4 ×10

−12

, (9.144)

=−7.2 ×10

−15

syr

−1

. (9.145)

The observed value as of 2004 is (Weisberg and Taylor 2005)

dP/dt =−(2.4184 ±0.0009) ×10

−12

. (9.146)

The effect has been observed in other binaries as well (Lorimer 2008).

9.5 Astrophysical sources of gravitational waves

Overview

Physicists and astronomers have made great efforts to understand what kinds of sources

of gravitational waves the current detectors might be able to see. This has been motivated

partly by the need to decide whether the large investment in these detectors is justiﬁed,

and partly because the sensitivity of the detectors depends on the accuracy with which

waveforms can be predicted, so that they can be recognized against detector noise. While

the astrophysics of potential sources is beyond the scope of this book, it is useful to review

the basic classes of sources, learn what general relativity says about them, and understand

why they might be interesting to observe. We shall consider four groups of sources: binary

systems, spinning neutron stars, gravitational collapse, and the Big Bang.

Binary systems

We have seen how to compute the expected wave amplitude from a binary system in Eqs.

(9.98) and (9.99), as well as in Exers. 29 and 39 in § 9.7. There are a number of known

binary systems in our Galaxy which ought, by these equations, to be radiating gravitational

waves in the frequency band observable by LISA, and with amplitudes well above LISA’s

expected instrumental noise. When LISA begins its observations, therefore, scientists will

be looking for these signals as proof that general relativity is correct at this basic level, as

well as that the spacecraft is operating properly.

The ground-based detectors will not, however, be looking for signals from long-lived

binary systems. The reason is evident if we combine some of our previous computations.

We have calculated what the gravitational wave luminosity of an equal-mass binary is