Schutz B. A first course in general relativity

Подождите немного. Документ загружается.

153 6.4 Parallel-transport, geodesics, and curvature

;α

√

− g

(

√

− gV

)

,α

. (6.42)

This is a very much easier formula to use than Eq. (6.36). It is also important for Gauss’

law, where we integrate the divergence over a volume (using, of course, the proper volume

element):

;α

√

− g d

x =

(

√

− gV

)

,α

x. (6.43)

Since the ﬁnal term involves simple partial derivatives, the mathematics of Gauss’ law

applies to it, just as in SR (§ 4.8):

(

√

− gV

)

,α

x =

(

√

− g d

S. (6.44)

This means

;α

√

− g d

x =

(

√

− g d

S. (6.45)

So Gauss’ law does apply on a curved manifold, in the form given by Eq. (6.45). We

need to integrate the divergence over proper volume and to use the proper surface element,

√

− g d

S, in the surface integral.

6.4 Parallel-transport, geodesics, and curvature

Until now, we have used the local-ﬂatness theorem to develop as much mathematics on

curved manifolds as possible without considering the curvature explicitly. Indeed, we have

yet to give a precise mathematical deﬁnition of curvature. It is important to distinguish

two different kinds of curvature: intrinsic and extrinsic. Consider, for example, a cylinder.

Since a cylinder is round in one direction, we think of it as curved. This is its extrinsic

curvature: the curvature it has in relation to the ﬂat three-dimensional space it is part of.

On the other hand, a cylinder can be made by rolling a ﬂat piece of paper without tearing

or crumpling it, so the intrinsic geometry is that of the original paper: it is ﬂat. This means

that the distance in the surface of the cylinder between any two points is the same as it was

in the original paper; parallel lines remain parallel when continued; in fact, all of Euclid’s

axioms hold for the surface of a cylinder. A two-dimensional ‘ant’ conﬁned to that surface

would decide it was ﬂat; only its global topology is funny, in that going in a certain direc-

tion in a straight line brings him back to where he started. The intrinsic geometry of an

n-dimensional manifold considers only the relationships between its points on paths that

154 Curved manifolds

remain in the manifold (for the cylinder, in the two-dimensional surface). The extrinsic cur-

vature of the cylinder comes from considering it as a surface in a space of higher dimension,

and asking about the curvature of lines that stay in the surface compared with ‘straight’

lines that go off it. So extrinsic curvature relies on the notion of a higher-dimensional

space. In this book, when we talk about the curvature of spacetime, we talk about its

intrinsic curvature, since it is clear that all world lines are conﬁned to remain in space-

time. Whether or not there is a higher-dimensional space in which our four-dimensional

space is an open question that is becoming more and more a subject of discussion within

the framework of string theory. The only thing of interest in GR is the intrinsic geometry of

spacetime.

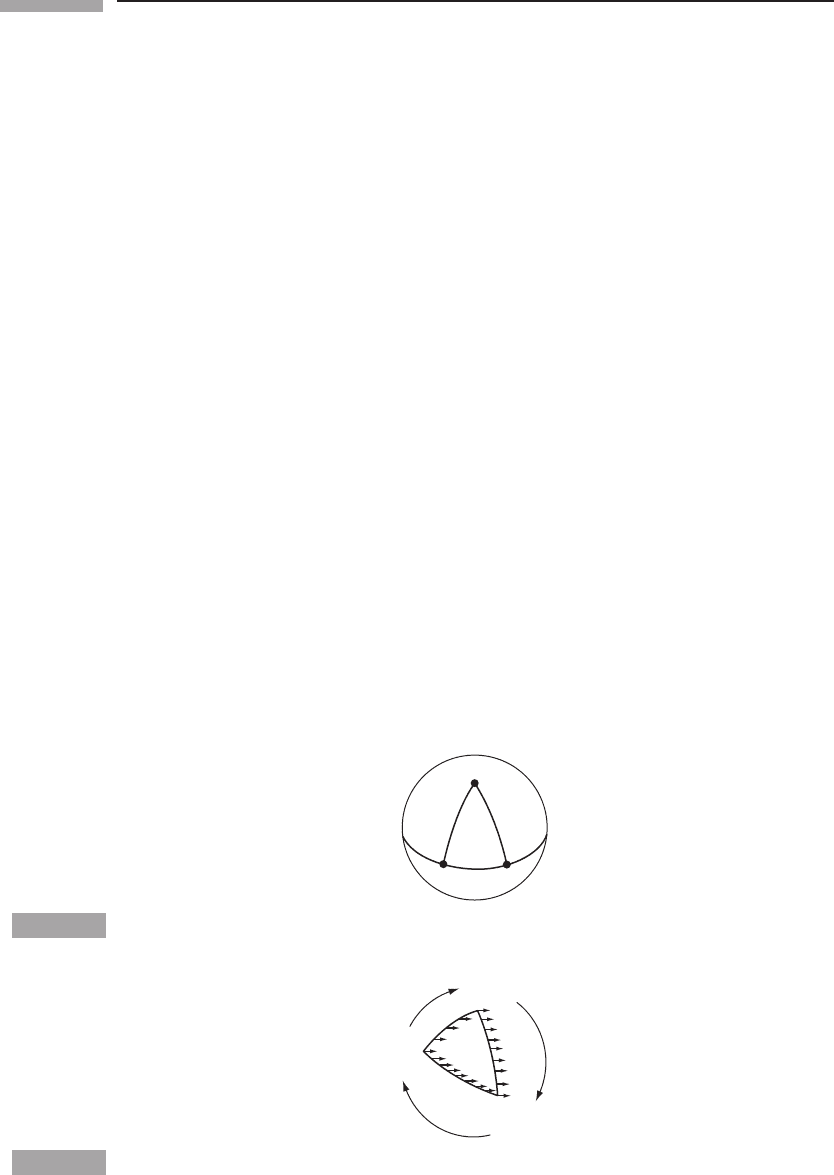
The cylinder, as we have just seen, is intrinsically ﬂat; a sphere, on the other hand, has an

intrinsically curved surface. To see this, consider Fig. 6.1, in which two neighboring lines

begin at A and B perpendicular to the equator, and hence are parallel. When continued as

locally straight lines they follow the arc of great circles, and the two lines meet at the pole

P. Parallel lines, when continued, do not remain parallel, so the space is not ﬂat.

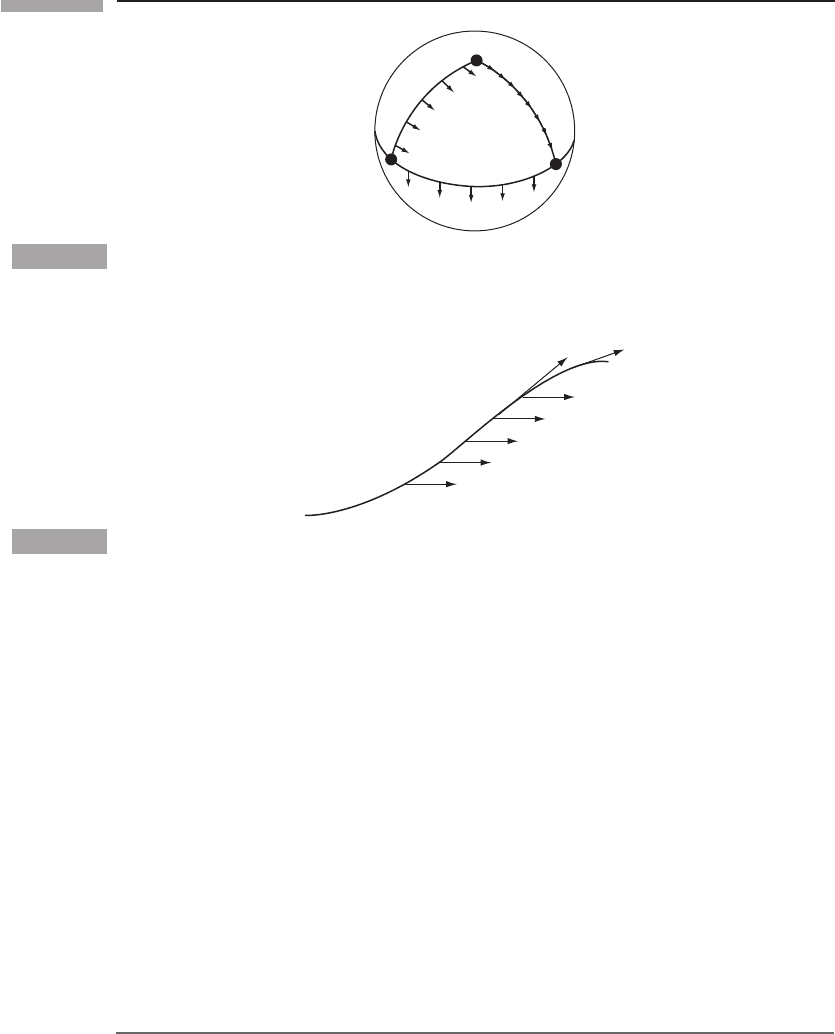
There is an even more striking illustration of the curvature of the sphere. Consider, ﬁrst,

ﬂat space. In Fig. 6.2 a closed path in ﬂat space is drawn, and, starting at A, at each point

a vector is drawn parallel to the one at the previous point. This construction is carried

around the loop from A to B to C and back to A. The vector ﬁnally drawn at A is, of course,

parallel to the original one. A completely different thing happens on a sphere! Consider

the path shown in Fig. 6.3. Remember, we are drawing the vector as it is seen to a two-

dimensional ant on the sphere, so it must always be tangent to the sphere. Aside from that,

each vector is drawn as parallel as possible to the previous one. In this loop, A and C are

on the equator 90

◦

apart, and B is at the pole. Each arc is the arc of a great circle, and

each is 90

◦

long. At A we choose the vector parallel to the equator. As we move up toward

B, each new vector is therefore drawn perpendicular to the arc AB. When we get to B,

Figure 6.1

A spherical triangle APB.

Figure 6.2

A ‘triangle’ made of curved lines in ﬂat space.

155 6.4 Parallel-transport, geodesics, and curvature

Figure 6.3

Parallel transport around a spherical triangle.

→

Figure 6.4

Parallel transport of



V along



the vectors are tangent to BC. So, going from B to C, we keep drawing tangents to BC.

These are perpendicular to the equator at C, and so from C to A the new vectors remain

perpendicular to the equator. Thus the vector ﬁeld has rotated 90

◦

in this construction!

Despite the fact that each vector is drawn parallel to its neighbor, the closed loop has caused

a discrepancy. Since this doesn’t happen in ﬂat space, it must be an effect of the sphere’s

curvature.

This result has radical implications: on a curved manifold it simply isn’t possible to

deﬁne globally parallel vector ﬁelds. We can still deﬁne local parallelism, for instance how

to move a vector from one point to another, keeping it parallel and of the same length. But

the result of such ‘parallel transport’ from point A to point B depends on the path taken.

We therefore cannot assert that a vector at A is or is not parallel to (or the same as) a certain

vector at B.

Parallel-transport

The construction we have just made on the sphere is called parallel-transport. Suppose a

vector ﬁeld



V is deﬁned on the sphere, and we examine how it changes along a curve, as

in Fig. 6.4. If the vectors



V at inﬁnitesimally close points of the curve are parallel and of

equal length, then



V is said to be parallel-transported along the curve. It is easy to write

down an equation for this. If



U = dx/dλ is the tangent to the curve (λ being the parameter

156 Curved manifolds

along it;



U is not necessarily normalized), then in a locally inertial coordinate system at a

point P the components of



V must be constant along the curve at P:

dλ

= 0atP. (6.46)

This can be written as:

dλ

= U

,β

= U

;β

= 0atP. (6.47)

The ﬁrst equality is the deﬁnition of the derivative of a function (in this case V

) along the

curve; the second equality comes from the fact that 

μν

= 0atP in these coordinates.

But the third equality is a frame-invariant expression and holds in any basis, so it can be

taken as a frame-invariant deﬁnition of the parallel-transport of



V along



;β

= 0 ⇔

dλ



V =∇



V = 0. (6.48)

The last step uses the notation for the derivative along



U introduced in Eq. (3.67).

Geodesics

The most important curves in ﬂat space are straight lines. One of Euclid’s axioms is that

two straight lines that are initially parallel remain parallel when extended. What does he

mean by ‘extended’? He doesnít mean ‘continued in such a way that the distance between

them remains constant’, because even then they could both bend. What he means is that

each line keeps going in the direction it has been going in. More precisely, the tangent to

the curve at one point is parallel to the tangent at the previous point. In fact, a straight line

in Euclidean space is the only curve that parallel-transports its own tangent vector! In a

curved space, we can also draw lines that are ‘as nearly straight as possible’ by demanding

parallel-transport of the tangent vector. These are called geodesics:

{



Uis tangent to a geodesic}⇔∇



U = 0. (6.49)

(Note that in a locally inertial system these lines are straight.) In component notation:

;β

= U

,β

+ 

μβ

= 0. (6.50)

Now, if we let λ be the parameter of the curve, then U

= dx

/dλ and U

∂/∂x

= d/dλ:

dλ



dλ



+ 

μβ

dλ

= 0. (6.51)

157 6.5 The curvature tensor

Since the Christoffel symbols 

μβ

are known functions of the coordinates {x

},thisis

a nonlinear (quasi-linear), second-order differential equation for x

(λ). It has a unique

solution when initial conditions at λ = λ

are given: x

= x

(λ

) and U

= (dx

/dλ)

So, by giving an initial position (x

) and an initial direction (U

), we get a unique

geodesic.

Recall that if we change parameter, we change, mathematically speaking, the curve

(though not the points it passes through). Now, if λ is a parameter of a geodesic (so that

Eq. (6.51) is satisﬁed), and if we deﬁne a new parameter

φ = aλ + b, (6.52)

where a and b are constants (not depending on position on the curve), then φ is also a

parameter in which Eq. (6.51) is satisﬁed:

dφ

+ 

μβ

dφ

= 0.

Generally speaking, only linear transformations of λ like Eq. (6.52) will give new param-

eters in which the geodesic equation is satisﬁed. A parameter like λ and φ above is called

an afﬁne parameter. A curve having the same path as a geodesic but parametrized by a

nonafﬁne parameter is, strictly speaking, not a geodesic curve.

A geodesic is also a curve of extremal length between any two points: its length is

unchanged to ﬁrst order in small changes in the curve. The student is urged to prove this

by using Eq. (6.7), ﬁnding the Euler–Lagrange equations for it to be an extremal for ﬁxed

and λ

, and showing that these reduce to Eq. (6.51) when Eq. (6.32) is used. This is a

very instructive exercise. We can also show that proper distance along the geodesic is itself

an afﬁne parameter (see Exers. 13–15, § 6.9).

6.5 T h e cu r vat u re te n so r

At last we are in a position to give a mathematical description of the intrinsic curvature

of a manifold. We go back to the curious example of the parallel-transport of a vector

around a closed loop, and take it as our deﬁnition of curvature. Let us imagine in our

manifold a very small closed loop (Fig. 6.5) whose four sides are the coordinate lines

= b + δb

= a + δa

= b

= a

Figure 6.5

Small section of a coordinate grid.

158 Curved manifolds

= a, x

= a + δa, x

= b, and x

= b +δb. A vector



V deﬁned at A is parallel-

transported to B. The parallel-transport law ∇

e



V = 0 has the component form

∂V

∂x

=−

μ1

. (6.53)

Integrating this from A to B gives

(B) = V

(A) +

∂V

∂x

= V

(A) −



μ1

(6.54)

where the notation ‘x

= b’ under the integral denotes the path AB. Similar transport from

B to C to D gives

(B) −

=a+δa



μ2

, (6.55)

(D) = V

=b+δb



μ1

. (6.56)

The integral in the last equation has a different sign because the direction of transport

from C to D is in the negative x

direction. Similarly, the completion of the loop gives

ﬁnal

) = V

(D) +



μ2

. (6.57)

The net change in V

(A) is a vector δV

, found by adding Eqs. (6.54)–(6.57):

δV

= V

ﬁnal

) − V

initial

)



μ2

−

=a+δa



μ2

=b+δb



μ1

−



μ1

. (6.58)

Notice that these would cancel in pairs if 

μν

and V

were constants on the loop, as they

would be in ﬂat space. But in curved space they are not, so if we combine the integrals over

similar integration variables and work to ﬁrst order in the separation in the paths, we get to

lowest order,

δV

−

b+δb

δa

∂

∂x

(

μ2

)dx

a+δa

δb

∂

∂x

(

μ1

)dx

(6.59)

≈ δa δb

−

∂

∂x

(

μ2

) +

∂

∂x

(

μ1

)

. (6.60)

This involves derivatives of Christoffel symbols and of V

. The derivatives V

can be

eliminated using Eq. (6.53) and its equivalent with 1 replaced by 2. Then Eq. (6.60)

becomes

δV

= δa δb



μ1,2

− 

μ2,1

+ 

ν2



μ1

− 

ν1



μ2

. (6.61)

159 6.5 The curvature tensor

(To obtain this, we need to relabel dummy indices in the terms quadratic in s.) Notice

that this turns out to be just a number times V

, summed on μ. Now, the indices 1 and 2

appear because the path was chosen to go along those coordinates. It is antisymmetric in

1 and 2 because the change δV

would have to have the opposite sign if we went around

the loop in the opposite direction (that is, interchanging the roles of 1 and 2). If we used

general coordinate lines x

and x

, we would ﬁnd

δV

= change in V

due to transport, ﬁrst δa e

, then δb e

then −δa a

, and ﬁnally −δb e

= δa δb



μσ ,λ

− 

μλ,σ

+ 

νλ



μσ

− 

νσ



μλ

. (6.62)

Now, δV

depends on δa δb, the coordinate ‘area’ of the loop. So it is clear that if the

length of the loop in one direction is doubled, δV

is doubled. This means that δV

depends

linearly on δa e

and δb e

. Moreover, it certainly also depends linearly in Eq. (6.62)on

itself and on ˜ω

, which is the basis one-form that gives δV

from the vector δ



V. Hence

we have the following result: if we deﬁne

βμν

:= 

βν,μ

− 

βμ,ν

+ 

σμ



βν

− 

σν



βμ

, (6.63)

then R

βμν

must be components of the





tensor which, when supplied with arguments

˜ω



V, δa e

, δb e

,givesδV

, the component of the change in



V after parallel-transport

around a loop given by δa e

and δb e

. This tensor is called the Riemann curvature

tensor R.

It is useful to look at the components of R in a locally inertial frame at a point P.We

have 

μν

= 0atP, but we can ﬁnd its derivative from Eq. (6.32):



μν,σ

αβ



βμ,νσ

+ g

βν,μσ

− g

μν,βσ



. (6.64)

Since second derivatives of g

αβ

don’t vanish, we get at P

βμν

ασ

σβ,νμ

+ g

σν,βμ

− g

βν,σμ

− g

σβ,μν

− g

σμ,βν

+ g

βμ,σν

). (6.65)

Using the symmetry of g

αβ

and the fact that

αβ,μν

= g

αβ,νμ

, (6.66)

because partial derivatives always commute, we ﬁnd at P

βμν

σσ



σν,βμ

− g

σμ,βν

+ g

βμ,σν

− g

βν,σμ



. (6.67)

If we lower the index α, we get (in the locally ﬂat coordinate system at its origin P)

As with other deﬁnitions we have earlier introduced, there is no universal agreement about the overall sign of

the Riemann tensor, or even on the placement of its indices. Always check the conventions of whatever book

you read.

160 Curved manifolds

αβμν

:= g

αλ

βμν



αν,βμ

− g

αμ,βν

+ g

βμ,αν

− g

βν,αμ



. (6.68)

In this form it is easy to verify the following identities:

αβμν

=−R

βαμν

=−R

αβνμ

= R

μναβ

, (6.69)

αβμν

+ R

ανβμ

+ R

αμνβ

= 0. (6.70)

Thus, R

αβμν

is antisymmetric on the ﬁrst pair and on the second pair of indices, and

symmetric on exchange of the two pairs. Since Eqs. (6.69) and (6.70) are valid tensor

equations true in one coordinate system, they are true in all bases. (Note that an equa-

tion like Eq. (6.67) is not a valid tensor equation, since it involves partial derivatives, not

covariant ones. Therefore it is true only in the coordinate system in which it was derived.)

It can be shown (Exer. 18, § 6.9) that the various identities, Eqs. (6.69) and (6.70),

reduce the number of independent components of R

αβμν

(and hence of R

βμν

) to 20, in

four dimensions. This is, not coincidentally, the same number of independent g

αβ,μν

that

we found at the end of § 6.2 could not be made to vanish by a coordinate transformation.

Thus R

βμν

characterizes the curvature in a tensorial way.

A ﬂat manifold is one which has a global deﬁnition of parallelism: a vector can be moved

around parallel to itself on an arbitrary curve and will return to its starting point unchanged.

This clearly means that

βμν

= 0 ⇔ ﬂat manifold. (6.71)

(Try showing that this is true in polar coordinates for the Euclidean plane.)

An important use of the curvature tensor comes when we examine the consequences of

taking two covariant derivatives of a vector ﬁeld



V. We found in § 6.3 that ﬁrst derivatives

were like ﬂat-space ones, since we could ﬁnd coordinates in which the metric was ﬂat to

ﬁrst order. But second derivatives are a different story:

∇

=∇

;β

)

= (V

;β

)

,α

+ 

σα

;β

− 

βα

;σ

. (6.72)

In locally inertial coordinates whose origin is at P, all the s are zero, but their partial

derivatives are not. Therefore we have at P

∇

= V

,βα

+ 

νβ,α

. (6.73)

Bear in mind that this expression is valid only in this specially chosen coordinates system,

and that is true also for Eqs. (6.74) through (6.76) below. These coordinates make the

computation easier: consider now Eq. (6.73) with α and β exchanged:

∇

= V

,αβ

+ 

να,β

. (6.74)

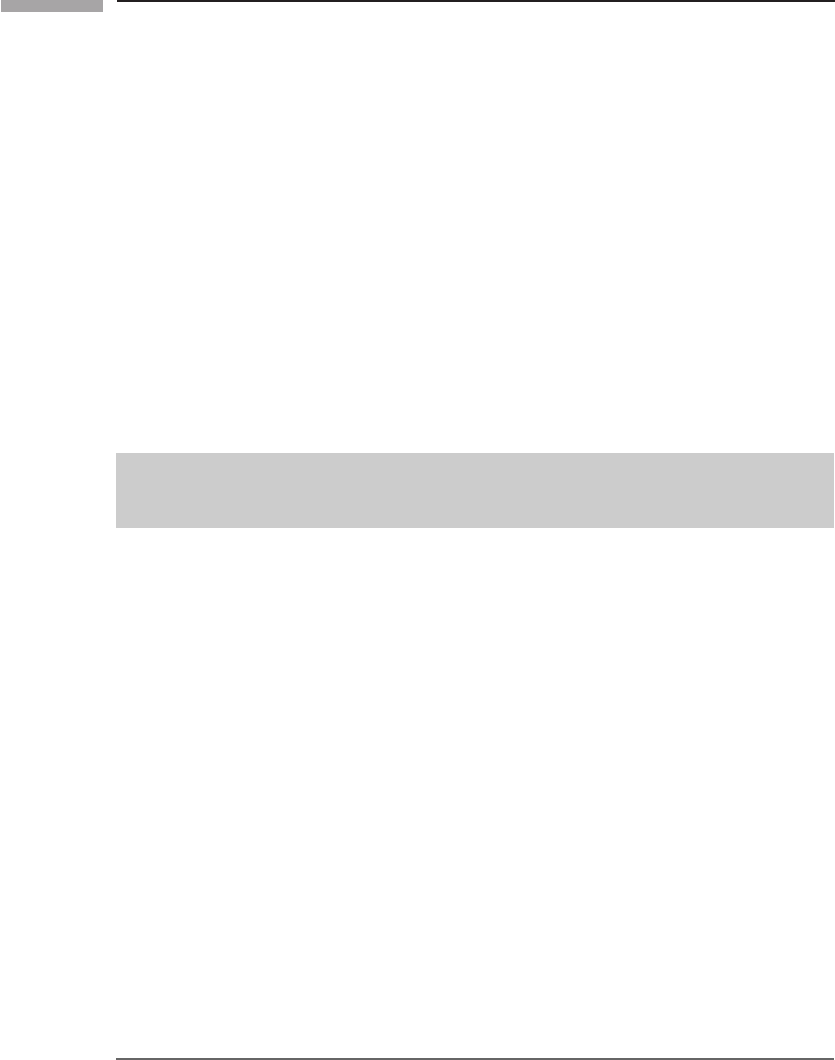
161 6.5 The curvature tensor

If we subtract these, we get the commutator of the covariant derivative operators ∇

and

∇

, written in the same notation as we would employ in quantum mechanics:

[∇

, ∇

:=∇

∇

−∇

∇





νβ,α

− 

να,β



. (6.75)

The terms involving the second derivatives of V

drop out here, since

,αβ

= V

,βα

. (6.76)

[Let us pause to recall that V

,α

is the partial derivative of the component V

,sobythe

laws of partial differentiation the partial derivatives must commute. On the other hand,

∇

is a component of the tensor ∇



V, and ∇

∇

is a component of ∇∇



V: there is no

reason (from differential calculus) why it must be symmetric on α and β. We have proved,

by showing that Eq. (6.75) is nonzero, that the double covariant derivative generally is not

symmetric.] Now, in this frame (where 

αβ

= 0atP), we can compare Eq. (6.75) with

Eq. (6.63) and see that at P

[∇

, ∇

= R

ναβ

. (6.77)

Now, this is a valid tensor equation, so it is true in any coordinate system: the Riemann

tensor gives the commutator of covariant derivatives. We can drop the restriction to locally

inertial coordinates: they were simply a convenient way of arriving at a general tensor

expression for the commutator. What this means is that in curved spaces, we must be

careful to know the order in which covariant derivatives are taken: they do not commute.

This can be extended to tensors of higher rank. For example, a





tensor has

[∇

, ∇

= R

σαβ

+ R

αβ

. (6.78)

That is, each index gets a Riemann tensor on it, and each one comes in with a +sign. (They

must all have the same sign because raising and lowering indices with g is unaffected by

∇

, since ∇g = 0.)

Eq. (6.77) is closely related to our original derivation of the Riemann tensor from

parallel-transport around loops, because the parallel-transport problem can be thought of

as computing, ﬁrst the change of



V in one direction, and then in another, followed by

subtracting changes in the reverse order: this is what commuting covariant derivatives

also does.

Geodesic deviation

We have often mentioned that in a curved space, parallel lines when extended do not remain

parallel. This can now be formulated mathematically in terms of the Riemann tensor. Con-

sider two geodesics (with tangents



V and





) that begin parallel and near each other,

as in Fig. 6.6, at points A and A



. Let the afﬁne parameter on the geodesics be called λ.

162 Curved manifolds

A′

V′

ξ(A)

Δλ

B′

→

ξ(B)

→

Figure 6.6

A connecting vector



ξ between two geodesics connects points of the same parameter value.

We deﬁne a ‘connecting vector’



ξ which ‘reaches’ from one geodesic to another, con-

necting points at equal intervals in λ (i.e. A to A



, B to B



, etc.). For simplicity, let us

adopt a locally inertial coordinate system at A, in which the coordinate x

points along the

geodesics and advances at the same rate as λ there (this is just a scaling of the coordinate).

Then because V

= dx

/dλ,wehaveatAV

= δ

. The equation of the geodesic at A is

dλ

= 0, (6.79)

since all Christoffel symbols vanish at A. The Christoffel symbols do not vanish at A



,so

the equation of the geodesic





at A



dλ



+ 



) = 0, (6.80)

where again at A



we have arranged the coordinates so that V

= δ

. But, since A and A



are separated by



ξ,wehave





)

∼



00,β

, (6.81)

the right-hand side being evaluated at A.WithEq.(6.80)thisgives

dλ



=−

00,β

. (6.82)

Now, the difference x

(λ, geodesic





) − x

(λ, geodesic



V) is just the component ξ

of the

vector



ξ. Therefore, at A,wehave

dλ



−

dλ

=−

00,β

. (6.83)

This then gives how the components of



ξ change. But since the coordinates are to some

extent arbitrary, we want to have, not merely the second derivative of the component ξ

but the full second covariant derivative ∇

∇



ξ . We can use Eq. (6.48) to obtain

∇

=∇

(∇

)

dλ

(∇

) = 

β0

(∇

). (6.84)