Schutz B. A first course in general relativity

Подождите немного. Документ загружается.

123 5.2 Tensor algebra in polar coordinates

→

dθ

→

dθ

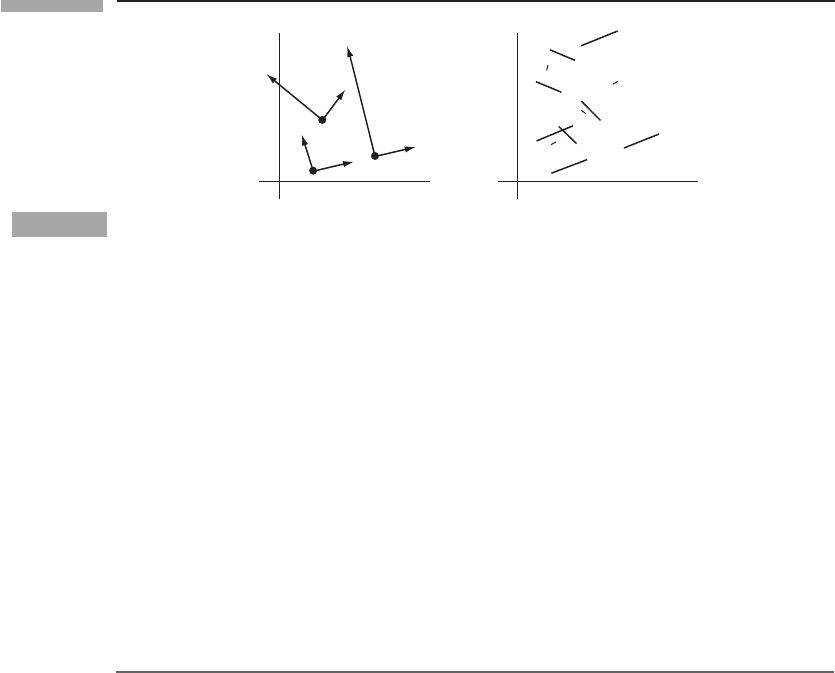
Figure 5.5

Basis vectors and one-forms for polar coordinates.

point. Moreover, the lengths of the bases are not constant. For example, from Eq. (5.23)

we ﬁnd

|e

==e

·e

= r

sin

θ +r

cos

θ = r

, (5.28a)

so that e

increases in magnitude as we get further from the origin. The reason is that

the basis vector e

, having components (0,1) with respect to r and θ , has essentially a θ

displacement of one unit, i.e. one radian. It must be longer to do this at large radii than at

small. So we do not have a unit basis. It is easy to verify that

|e

|=1, |

dr|=1, |

dθ|=r

−1

. (5.28b)

Again, |

dθ| gets larger (more intense) near r = 0 because a given vector can span a larger

range of θ near the origin than farther away.

Metric tensor

The dot products above were all calculated by knowing the metric in Cartesian coordi-

nates x, y:

e

·e

=e

·e

= 1, e

·e

= 0;

or, put in tensor notation,

g(e

, e

) = δ

αβ

in Cartesian coordinates. (5.29)

What are the components of g in polar coordinates? Simply



= g(e



, e



) =e



·e



(5.30)

or, by Eq. (5.28),

= 1, g

θθ

= r

, (5.31a)

and, from Eqs. (5.22) and (5.23),

rθ

= 0. (5.31b)

So we can write the components of g as

αβ

)

polar



0 r



, (5.32)

124 Prefacetocurvature

A convenient way of displaying the components of g and at the same time showing

the coordinates is the line element, which is the magnitude of an arbitrary ‘inﬁnitesimal’

displacement d



l · d



l = ds

=|dr e

+ dθe

= dr

+ r

dθ

. (5.33)

Do not confuse dr and dθ here with the basis one-forms

dr and

dθ. The things in this

equation are components of d



l in polar coordinates, and ‘d’ simply means ‘inﬁnitesimal ’.

There is another way of deriving Eq. (5.33) which is instructive. Recall Eq. (3.26)in

which a general





tensor is written as a sum over basis





tensors

⊗

.Forthe

metric this is

g = g

αβ

⊗

dr ⊗

dr +r

dθ ⊗

dθ.

Although this has a superﬁcial resemblance to Eq. (5.33), it is different: it is an oper-

ator which, when supplied with the vector d



l, the components of which are dr and dθ,

gives Eq. (5.33). Unfortunately, the two expressions resemble each other rather too closely

because of the confusing way notation has evolved in this subject. Most texts and research

papers still use the ‘old-fashioned’ form in Eq. (5.33) for displaying the components of the

metric, and we follow the same practice.

The metric has an inverse:



0 r



−1



0 r

−2



. (5.34)

So we have g

= 1, g

rθ

= 0, g

θθ

= 1/r

. This enables us to make the mapping between

one-forms and vectors. For instance, if φ is a scalar ﬁeld and

dφ is its gradient, then the

vector



dφ has components

(



dφ)

= g

αβ

,β

, (5.35)

(



dφ)

= g

rβ

,β

= g

+ g

rθ

,θ

= ∂φ/∂r; (5.36a)

(



dφ)

= g

θr

+ g

θθ

,θ

∂φ

∂θ

. (5.36b)

So, while (φ

, φ

,θ

) are components of a one-form, the vector gradient has components

(φ

, φ

,θ

). Even though we are in Euclidean space, vectors generally have different com-

ponents from their associated one-forms. Cartesian coordinates are the only coordinates in

which the components are the same.

125 5.3 Tensor calculus in polar coordinates

5.3 Tensor calculus in polar coordinates

The fact that the basis vectors of polar coordinates are not constant everywhere, leads

to some problems when we try to differentiate vectors. For instance, consider the simple

vector e

, which is a constant vector ﬁeld, the same at any point. In polar coordinates

it has components e

→ (

, 

) = (cos θ, −r

−1

sin θ). These are clearly not constant,

even though e

is. The reason is that they are components on a nonconstant basis. If

we were to differentiate them with respect to, say, θ, we would most certainly not get

∂e

/∂θ, which must be identically zero. So, from this example, we see that differentiat-

ing the components of a vector does not necessarily give the derivative of the vector. We

must also differentiate the nonconstant basis vectors. This is the key to the understand-

ing of curved coordinates and, indeed, of curved spaces. We shall now make these ideas

systematic.

Derivatives of basis vectors

Since e

and e

are constant vector ﬁelds, we easily ﬁnd that

∂

∂r

e

∂

∂r

(cos θ e

+ sin θ e

) = 0, (5.37a)

∂

∂θ

e

∂

∂θ

(cos θe

+ sin θ e

)

=−sin θ e

+ cos θe

e

. (5.37b)

These have a simple geometrical picture, shown in Fig. 5.6. At two nearby points, A and

B, e

must point directly away from the origin, and so in slightly different directions. The

derivative of e

with respect to θ is just the difference between e

at A and B divided by θ .

Δθ

Figure 5.6

Change in



,whenθ changes by θ.

126 Prefacetocurvature

The difference in this case is clearly a vector parallel to e

, which then makes Eq. (5.37b)

reasonable.

Similarly,

∂

∂r

e

∂

∂r

(−r sin θ e

+ r cos θ e

)

=−sin θe

+ cos θ e

e

, (5.38a)

∂

∂θ

e

=−r cos θ e

− r sin θ e

=−r e

. (5.38b)

The student is encouraged to draw a picture similar to Fig. 5.6 to explain these formulas.

Derivatives of general vectors

Let us go back to the derivative of e

. Since

e

= cos θ e

−

sin θ e

, (5.39)

we have

∂

∂θ

e

∂

∂θ

(cos θ) e

+ cos θ

∂

∂θ

(e

)

−

∂

∂θ



sin θ



e

−

sin θ

∂

∂θ

(e

) (5.40)

=−sin θ e

+ cos θ



e



−

cos θ e

−

sin θ(−r e

). (5.41)

To get this we used Eqs. (5.37) and (5.38). Simplifying gives

∂

∂θ

e

= 0, (5.42)

just as we should have. Now, in Eq. (5.40) the ﬁrst and third terms come from differen-

tiating the components of e

on the polar coordinate basis; the other two terms are the

derivatives of the polar basis vectors themselves, and are necessary for cancelling out the

derivatives of the components.

A general vector



V has components (V

, V

) on the polar basis. Its derivative, by analogy

with Eq. (5.40), is

∂



∂r

∂

∂r

e

+ V

e

)

∂V

∂r

e

+ V

∂e

∂r

∂V

∂r

e

+ V

∂e

∂r

and similarly for ∂



V/∂θ . Written in index notation, this becomes

∂



∂r

∂

∂r

e

) =

∂V

∂r

e

+ V

∂e

∂r

(Here α runs of course over r and θ .)

127 5.3 Tensor calculus in polar coordinates

This shows explicitly that the derivative of



V is more than just the derivative of

its components V

. Now, since r is just one coordinate, we can generalize the above

equation to

∂



∂x

∂V

∂x

e

+ V

∂e

∂x

, (5.43)

where, now, x

can be either r or θ for β = 1or2.

The Christoffel symbols

The ﬁnal term in Eq. (5.43) is obviously of great importance. Since ∂e

/∂x

is itself a

vector, it can be written as a linear combination of the basis vectors; we introduce the

symbol 

αβ

to denote the coefﬁcients in this combination:

∂e

∂x

= 

αβ

e

. (5.44)

The interpretation of 

αβ

is that it is the μth component of ∂e

/∂x

. It needs three

indices: one (α) gives the basis vector being differentiated; the second (β)givesthe

coordinate with respect to which it is being differentiated; and the third (μ) denotes the

component of the resulting derivative vector. These things, 

αβ

, are so useful that they

have been given a name: the Christoffel symbols. The question of whether or not they are

components of tensors we postpone until much later.

We have of course already calculated them for polar coordinates. From Eqs. (5.37) and

(5.38) we ﬁnd

(1) ∂e

/∂r = 0 ⇒ 

= 0 for all μ,

(2) ∂e

/∂θ =

e

⇒ 

rθ

= 0, 

rθ

(3) ∂e

/∂r =

e

⇒ 

θr

= 0, 

θr

(4) ∂e

/∂θ =−r e

⇒ 

θθ

=−r, 

θθ

= 0.

⎫

⎪

⎬

⎪

⎭

(5.45)

In the deﬁnition, Eq. (5.44), all indices must refer to the same coordinate system. Thus,

although we computed the derivatives of e

and e

by using the constancy of e

and e

the Cartesian bases do not in the end make any appearance in Eq. (5.45). The Christoffel

symbols’ importance is that they enable us to express these derivatives without using any

other coordinates than polar.

The covariant derivative

Using the deﬁnition of the Christoffel symbols, Eq. (5.44), the derivative in Eq. (5.43)

becomes

∂



∂x

∂V

∂x

e

+ V



αβ

e

. (5.46)

In the last term there are two sums, on α and μ. Relabeling the dummy indices will help

here: we change μ to α and α to μ and get

128 Prefacetocurvature

∂



∂x

∂V

∂x

e

+ V



μβ

e

. (5.47)

The reason for the relabeling was that, now, e

can be factored out of both terms:

∂



∂x



∂V

∂x

+ V



μβ



e

. (5.48)

So the vector ﬁeld ∂



V/∂x

has components

∂V

/∂x

+ V



μβ

. (5.49)

Recall our original notation for the partial derivative, ∂V

/∂x

= V

,β

. We keep this

notation and deﬁne a new symbol:

;β

:= V

,β

+ V



μβ

. (5.50)

Then, with this shorthand semicolon notation, we have

∂



V/∂x

= V

;β

e

, (5.51)

a very compact way of writing Eq. (5.48).

Now ∂



V/∂x

is a vector ﬁeld if we regard β as a given ﬁxed number. But there are two

values that β can have, and so we can also regard ∂



V/∂x

as being associated with a





tensor ﬁeld which maps the vector e

into the vector ∂



V/∂x

, as in Exer. 17, § 3.10.This

tensor ﬁeld is called the covariant derivative of



V, denoted, naturally enough, as ∇



V. Then

its components are

(∇



= (∇



= V

;β

. (5.52)

On a Cartesian basis the components are just V

,β

. On the curvilinear basis, however, the

derivatives of the basis vectors must be taken into account, and we get that V

;β

are the

components of ∇



V in whatever coordinate system the Christoffel symbols in Eq. (5.50)

refer to. The signiﬁcance of this statement should not be underrated, as it is the foundation

of all our later work. There is a single





tensor called ∇



V. In Cartesian coordinates its

components are ∂V

/∂x

. In general coordinates {x



} its components are called V



;β



and can be obtained in either of two equivalent ways: (i) compute them directly in {x



}

using Eq. (5.50) and a knowledge of what the 



coefﬁcients are in these coordinates;

or (ii) obtain them by the usual tensor transformation laws from Cartesian to {x



What is the covariant derivative of a scalar? The covariant derivative differs from the

partial derivative with respect to the coordinates only because the basis vectors change.

But a scalar does not depend on the basis vectors, so its covariant derivative is the same as

its partial derivative, which is its gradient:

∇

f = ∂f /∂x

; ∇f =

df . (5.53)

129 5.3 Tensor calculus in polar coordinates

Divergence and Laplacian

Before doing any more theory, let us link this up with things we have seen before. In

Cartesian coordinates the divergence of a vector V

is V

,α

. This is the scalar obtained

by contracting V

,β

on its two indices. Since contraction is a frame-invariant operation,

the divergence of



V can be calculated in other coordinates {x



} also by contracting the

components of ∇



V on their two indices. This results in a scalar with the value V



;α



.Itis

important to realize that this is the same number as V

,α

in Cartesian coordinates:

,α

≡ V



;β



, (5.54)

where unprimed indices refer to Cartesian coordinates and primed refer to the arbitrary

system.

For polar coordinates (dropping primes for convenience here)

;α

∂V

∂x

+ 

μα

Vμ.

Now, from Eq. (5.45) we can calculate



rα

=

+ 

rθ

= 1/r,



θα

= 

θr

+ 

θθ

= 0.



(5.55)

Therefore we have

;α

∂V

∂r

∂V

∂θ

∂

∂r

(rV

) +

∂

∂θ

. (5.56)

This may be a familiar formula to the student. What is probably more familiar is the Lapla-

cian, which is the divergence of the gradient. But we only have the divergence of vectors,

and the gradient is a one-form. Therefore we must ﬁrst convert the one-form to a vector.

Thus, given a scalar φ, we have the vector gradient (see Eq. (5.53) and the last part of § 5.2

above) with components (φ

, φ

,θ

). Using these as the components of the vector in the

divergence formula, Eq. (5.56)gives

∇·∇φ :=∇

φ =

∂

∂r



∂φ

∂r



∂

∂θ

. (5.57)

This is the Laplacian in plane polar coordinates. It is, of course, identically equal to

∇

φ =

∂

∂x

∂

∂y

. (5.58)

Derivatives of one-forms and tensors of higher types

Since a scalar φ depends on no basis vectors, its derivative

dφ is the same as its covariant

derivative ∇φ. We shall almost always use the symbol ∇φ. To compute the derivative of a

one-form (which as for a vector won’t be simply the derivatives of its components), we use

130 Prefacetocurvature

the property that a one-form and a vector give a scalar. Thus, if ˜p is a one-form and



V is an

arbitrary vector, then for ﬁxed β, ∇

˜p is also a one-form, ∇



V is a vector, and ˜p,



V≡φ

is a scalar. In any (arbitrary) coordinate system this scalar is just

φ = p

. (5.59)

Therefore ∇

φ is, by the product rule for derivatives,

∇

φ = φ

,β

∂p

∂x

+ p

∂V

∂x

. (5.60)

But we can use Eq. (5.50) to replace ∂V

/∂x

in favor of V

;β

, which are the components

of ∇



∇

φ =

∂p

∂x

+ p

;β

− p



μβ

. (5.61)

Rearranging terms, and relabeling dummy indices in the term that contains the Christoffel

symbol, gives

∇

φ =



∂p

∂x

− p



αβ



+ p

;β

. (5.62)

Now, every term in this equation except the one in parentheses is known to be the compo-

nent of a tensor, for an arbitrary vector ﬁeld



V. Therefore, since multiplication and addition

of components always gives new tensors, it must be true that the term in parentheses is also

the component of a tensor. This is, of course, the covariant derivative of ˜p:

(∇

˜p)

:= (∇˜p)

αβ

:= p

α;β

= p

α,β

− p



αβ

. (5.63)

Then Eq. (5.62) reads

∇

) = p

α;β

+ p

;β

. (5.64)

Thus covariant differentiation obeys the same sort of product rule as Eq. (5.60). It must

do this, since in Cartesian coordinates ∇ is just partial differentiation of components, so

Eq. (5.64) reduces to Eq. (5.60).

Let us compare the two formulae we have, Eq. (5.50) and Eq. (5.63):

;β

= V

,β

+ V



μβ

α;β

= p

α,β

− p



αβ

There are certain similarities and certain differences. If we remember that the derivative

index β is the last one on , then the other indices are the only ones they can be without

raising and lowering with the metric. The only thing to watch is the sign difference. It may

help to remember that 

μβ

was related to derivatives of the basis vectors, for then it is

reasonable that −

αβ

be related to derivatives of the basis one-forms. The change in sign

means that the basis one-forms change ‘oppositely’ to basis vectors, which makes sense

131 5.4 Christoffel symbols and the metric

when we remember that the contraction ˜ω

, e

=δ

is a constant, and its derivative

must be zero.

The same procedure that led to Eq. (5.63) would lead to the following:

∇

μν

= T

μν,β

− T

αν



μβ

− T

μα



νβ

; (5.64)

∇

μν

= A

μν

,β

+ A

αν



αβ

+ A

μα



αβ

; (5.65)

∇

= B

ν,β

+ B



αβ

− B



νβ

. (5.66)

Inspect these closely: they are very systematic. Simply throw in one  term for each index;

a raised index is treated like a vector and a lowered one like a one-form. The geometrical

meaning of Eq. (5.64)isthat∇

μν

is a component of the





tensor ∇T, where T is a





tensor. Similarly, in Eq. (5.65), A is a





tensor and ∇A is a





tensor with components

∇

μν

5.4 Christoffel symbols and the metric

The formalism developed above has not used any properties of the metric tensor to derive

covariant derivatives. But the metric must be involved somehow, because it can convert

a vector into a one-form, and so it must have something to say about the relationship

between their derivatives. In particular, in Cartesian coordinates the components of the

one-form and its related vector are equal, and since ∇ is just differentiation of components,

the components of the covariant derivatives of the one-form and vector must be equal.

This means that if



V is an arbitrary vector and

V = g(



V, ) is its related one-form, then in

Cartesian coordinates

∇

V = g(∇



V, ). (5.67)

But Eq. (5.67) is a tensor equation, so it must be valid in all coordinates. We conclude that

α;β

= g

αμ

;β

, (5.68)

which is the component representation of Eq. (5.67).

If the above argument in words wasn’t satisfactory, let us go through it again in equa-

tions. Let unprimed indices α, β, γ , ··· denote Cartesian coordinates and primed indices



, β



, γ



, ··· denote arbitrary coordinates.

We begin with the statement



= g



, (5.69)

valid in any coordinate system. But in Cartesian coordinates

αμ

= δ

αμ

, V

= V

132 Prefacetocurvature

Now, also in Cartesian coordinates, the Christoffel symbols vanish, so

α;β

= V

α,β

and V

;β

= V

,β

Therefore we conclude

α;β

= V

;β

in Cartesian coordinates only. To convert this into an equation valid in all coordinate

systems, we note that in Cartesian coordinates

;β

= g

αμ

;β

so that again in Cartesian coordinates we have

α;β

= g

αμ

;β

But now this equation is a tensor equation, so its validity in one coordinate system implies

its validity in all. This is just Eq. (5.68)again:



;β



= g



;β



(5.70)

This result has far-reaching implications. If we take the β



covariant derivative of

Eq. (5.69), we ﬁnd



;β



= g



;β



+ g



;β



Comparison of this with Eq. (5.70) shows (since



V is an arbitrary vector) that we must have



;β



≡ 0 (5.71)

in all coordinate systems. This is a consequence of Eq. (5.67). In Cartesian coordinates

αμ;β

≡ g

αμ,β

= δ

αμ,β

≡ 0

is a trivial identity. However, in other coordinates it is not obvious, so we shall work it out

as a check on the consistency of our formalism.

Using Eq. (5.64) gives (now unprimed indices are general)

αβ;μ

= g

αβ,μ

− 

αμ

νβ

− 

βμ

αν

. (5.72)

In polar coordinates let us work out a few examples. Let α = r, β = r, μ = r:

rr;r

= g

rr,r

− 

νr

− 

rν

Since g

rr,r

= 0 and 

= 0 for all ν, this is trivially zero. Not so trivial is α = θ,

β = θ, μ = r:

θθ;r

= g

θθ,r

− 

θr

νθ

− 

θr

θν

With g

θθ

= r

, 

θr

= 1/r and 

θr

= 0, this becomes

θθ ;r

= (r

)

−

) −

) = 0.