Scheideler C. Universal Routing Strategies for Interconnection Networks
Подождите немного. Документ загружается.


7.2 The Random Rank Protocol 79
el be the link on the routing path of Pl that has a distance of gl from its
destination. If Pl is fixed then el is fixed as well.
Now suppose that, for some i E {1,...,s}, pj and ej are fixed for all
1 < j < i. The problem is to bound the expected number of candidates for
Pi+l. Clearly, the routing path of Pi+l must traverse
ei,
and
Pi+l
must be
distinct from
Pl,...,Pi
because of the contention resolution rule. Let P be
the set of all packets. Since each packet chooses a random destination, the
expected number of possibilities to choose
Pi+l
is at most
E Pr~Vi+l traverses e~]
P,+I 6P\{Pl,-.-,pI}
-< E Pr~v,+l traverses
e~] = Ce, <_
P,+I EP
Let ei+l be the link on the routing path of pi+l that has a distance of ~i+1
from ei. Once pi+l is fixed then ei+l is fixed as well.
Altogether, the expected number of choices for p2,...
,Ps+l
(and therefore
e2,..., es) is at most ~s. Putting all pieces together yields the lemma. []
Since the packets choose their ranks independently at random, the prob-
ability that an s-delay sequence is active is
1/K s+l.
Thus
Pr[The random rank protocol needs >_ D + s steps]
< Pr[there exists an active s-delay sequence]
< (o+s) 1
-
s ks+l] K,+I
The rest is similar to the proof of Theorem 7.2.1.
As the expected congestion for routing h packets from each input node
to random intermediate destinations, and from random intermediate desti-
nations to their true destinations is both times bounded by hC, the runtime
bound of the theorem follows. Because the intermediate destinations of the
packets are chosen independently at random, applying Chernoff bounds yields
that the number of packets that want to traverse a link during the routing
is bounded by
O(hC +
logN), w.h.p. From this the bound for the buffer size
stated in the theorem follows. []
Theorem 7.2.2 can be applied, for instance, to routing in butterflies.
Theorem 7.2.3.
Every h-relation can be routed in a wrap-around butterfly
with N input/output nodes in time O(h + log N), w.h.p., using buffers of size
O(h +
log N).
Pro@
Let us consider the following path system for connecting the in-
puts with the outputs in a wrap-around butterfly: For each pair of nodes
((0, a), (0, f~)), where a
=
(ad-1...
ala0)2 and/3
=
(bd-1...
blbo)2,
the path

80 7. Oblivious Routing Protocols
from (0, a) to (d,/~) contains the nodes (0,ad-1 ...aia0), (1,ad-1 ...aib0),
(2, ad-1.., bibo) ... (d- 1, ad-ibd-2.., bo), (0, bd-i.., bo) in this order. This
path system has the following property.
Lemma 7.2.4. Consider any wrap-around butterfly with a path system as
described above. Then the expected congestion of routing a random h-function
from the inputs to the outputs is 89 h.
Proof. Consider an arbitrary edge e from level i to level (i + 1) mod d of a
d-dimensional wrap around butterfly, i E [d]. There are altogether 2 i nodes
in the top row that can reach e via paths in the path system described above.
Since we consider random h-functions, each of the h packets stored in these
nodes has a probability of (89 of choosing a path that runs through e.
Altogether this yields an expected congestion of 89 []
Using this result together with Theorem 7.2.2 yields Theorem 7.2.3. []
This means that any global permutation can be routed in a wrap-around
butterfly of size N in optimal time O(logN), w.h.p.
7.2.3 Limitations
The following observation shows that there are simple path systems for which
the random rank protocol performs poorly. Its proof can be found in [LMR94].
Observation 7.2.1. There exists a simple path collection of size n with
dilation D = O(logn/loglogn) and congestion C = O(logn/loglogn),
where the expected routing time of the random rank protocol is bounded by
12((log n/log log
n)3/2).
The path collection used for this observation consists of many subcollec-
tions of paths. Each subcollection consists of a linear array of length D, with
loops of length V~ between adjacent nodes (see Figure 7.2).
~~ ...
Fig. 7.2. The counterexa.mple.
The packets traversing each subcollection of paths are broken into
groups numbered 0 through v/D- 1 of v~ packets each. The packets in
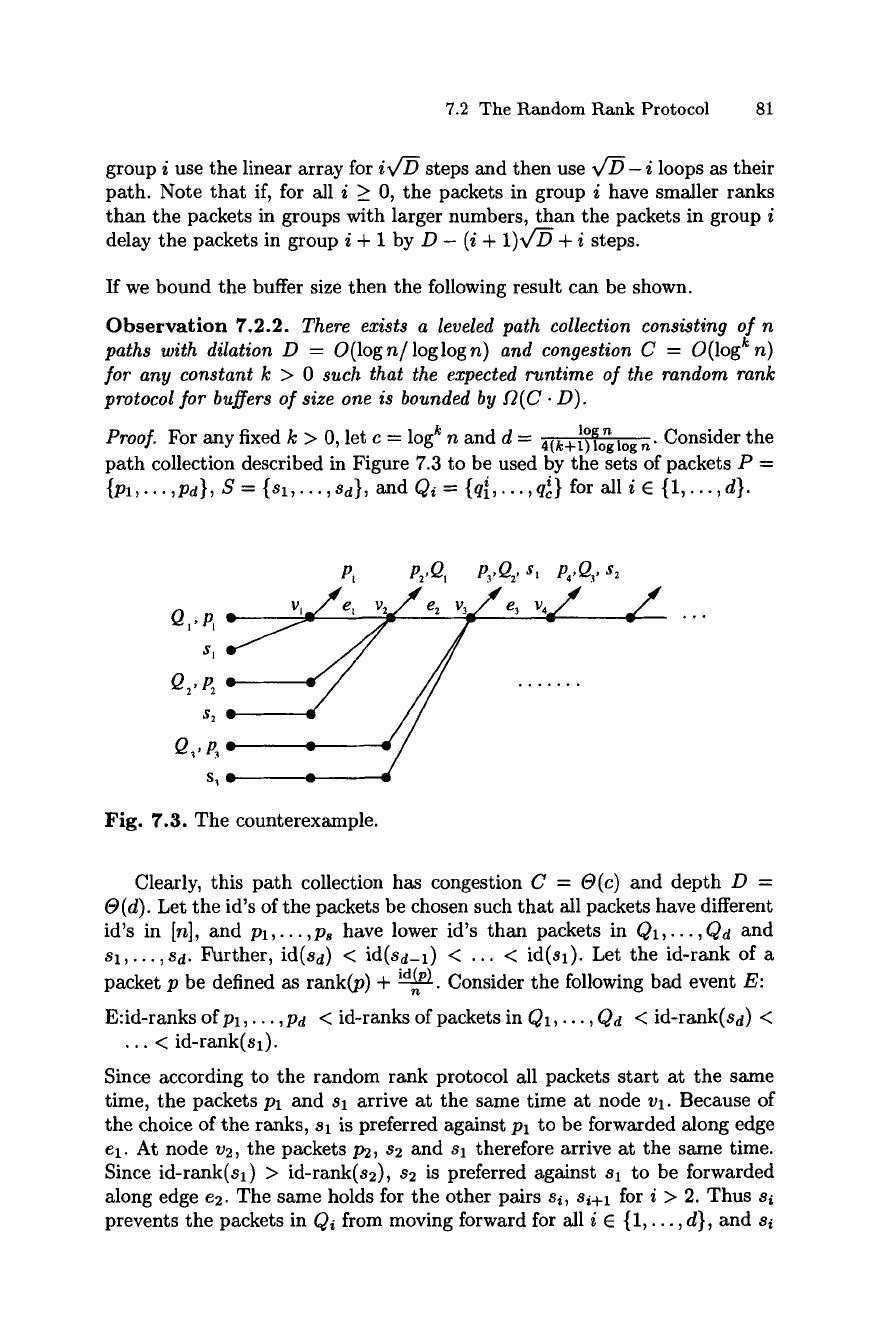
7.2 The Random Rank Protocol 81
group i use the linear array for iv/-D steps and then use v/D- i loops as their
path. Note that if, for all i _> 0, the packets in group i have smaller ranks
than the packets in groups with larger numbers, than the packets in group i
delay the packets in group i + 1 by D - (i + 1)~ + i steps.
If we bound the buffer size then the following result can be shown.
Observation 7.2.2. There exists a leveled path collection consisting of n
paths with dilation D = O(logn/loglogn) and congestion C = O(logkn)
for any constant k > 0 such that the expected runtime of the random rank
protocol for buffers of size one is bounded by T2(C. D).
1o~ n
Proof. For any fixed k > 0, let c = log k n and d = 4(k+Dtoslog,~" Consider the
path collection described in Figure 7.3 to be used by the sets of packets P =
{Pl,...,Pd}, S = {sl,...,Sd}, and Qi = {q~,...,qe/} for all i 9 {1,...,d}.
P~
vt Je
Q"P''~- ~ /
,,.- i// //
o:::
o,p,- - :/
p~,Q, p3,Q2, S, pa, Q3,
s 2
v2J e 2 v~J e 3 v4J J
Fig. 7.3. The counterexample.
Clearly, this path collection has congestion C = O(c) and depth D =
O(d). Let the id's of the packets be chosen such that all packets have different
id's in [n], and pl,...,Ps have lower id's than packets in Q1,...,Qd and
sl,...,sa. Further, id(sd) < id(sd-x) < ... < id(sl). Let the id-rank of a
packet p be defined as rank(p) + ~ Consider the following bad event E:
?% "
E:id-ranks of pl,... ,Pd < id-ranks of packets in Q1,..., Qd < id-rank(sd) <
... < id-rank(Sl).
Since according to the random rank protocol all packets start at the same
time, the packets Pl and sl arrive at the same time at node va. Because of
the choice of the ranks, sl is preferred against Pl to be forwarded along edge
el. At node v2, the packets P2, s2 and st therefore arrive at the same time.
Since id-rank(sl) > id-rank(s2), s2 is preferred against Sl to be forwarded
along edge e2. The same holds for the other pairs si, si+l for i > 2. Thus si
prevents the packets in Qi from moving forward for all i E { 1,..., d}, and si

82 7. Oblivious Routing Protocols
can only be moved forward along ei+l if packet si+l and all packets in Qi+l
have been moved along link ei+l. Hence the routing takes ~(c. d) = ~2(C- D)
steps.
In the following we will bound the probability that such a bad event
occurs. We start with computing a lower bound for the number of orderings
of the (c+ 2)d packets that the bad event. The number of ways to obtain such
an ordering is
d!(c. d)!.
Clearly, there are ((c + 2)d)! possibilities to choose
an arbitrary ordering for all (c + 2)d packets. For a randomly chosen order of
id's and randomly chosen ranks, it holds because of symmetry reasons that
every ordering of the id-ranks has the same probability to occur. If we choose
the id's for the packets in such a way that they support the ordering in E,
then we get a probability of at least
((c+ 2)d)! > >
- ((e C2)d)2 (e + - d(e
+ 2)
1o~ n for any constant k > 0
that E is true. For c-- logkn and d = 4(k-bl)loglogn
this probability is at least
1In 2/3.
Since a path collection of size n can consist
of O(c.--~) sub-collections as described in Figure 7.3, the expected number of
sub-collections that fulfill E is at least one. This yields the observation. D
The following protocol removes this drawback.
7.3 Ranade's
Protocol
Consider the problem of routing packets in leveled networks with bounded
degree and bounded buffers. As we will see, this can be done efficiently by a
protocol we call
Ranade's protocol
(see also [Le92]). The difference between
this and the previous protocol is that Ranade's protocol sends in addition to
the usual packets so-called "ghost packets". This extension was first described
by Ranade IRa91] and generalized by Leighton
et al.
[LMRR94]. Ghost pack-
ets help the algorithm to maintain the following invariant:
A packet is routed along an edge only after all the other packets with
lower ranks that must pass through the edge have done so.
7.3.1 Description of
the Protocol
At the beginning every packet p gets a random rank(p) E [K] that is stored in
its routing information (K is determined later). Furthermore a special end-
of-stream (EOS) packet is inserted into the injection buffer, and is assigned
rank K. Consider each
incoming
link to have space for storing at most q > 1
packets. In each time step, the algorithm then operates as follows.

7.3 Ranade's Protocol 83
For each node v with at least one nonempty buffer,
-
select a packet p according to the priority rule (see Section 7.2.1),
-
if the buffer of the next link on p's path contains fewer than q
packets at the beginning of that step then send p out,
-
send out a ghost packet with the rank of p along all other links,
- kill ghost packets that have been in a buffer in v at the beginning
of that step.
Since each incoming link has its own buffer, a link buffer is therefore
guaranteed never to hold more than q packets.
Ghost packets are sent to prevent buffers from getting empty. By complete
induction it is easy to show that in this case all nodes send out packets in
order of strictly increasing rank during the routing: If node v at level i sends
out packets in order of strictly increasing rank, the rank of the ghost packets
sent out along all other edges leaving v provides the receiving nodes at level
i + 1 with a lower bound on the ranks of the packets they will receive from v
in the future. Therefore a node at level i + 1 is also able to send out packets
in order of strictly increasing rank.
End-of-stream packets are given a special treatment. Since an EOS packet
has rank K, it can not be selected by a node unless there is only an EOS
packet left in the node's injection buffer and in each of the buffers on all of
the node's incoming links. Once an EOS packet has been selected, the node
will create a new EOS packet for each of its outgoing edges, and each edge
will attempt to send the corresponding packet at each step until it succeeds.
After sending an EOS packet along an edge, a node will not send any more
packets along that edge.
Ranade's protocol has the following runtime (see [LMRR94, Le92] for a
proof).
Theorem 7.3.1.
Let G be an arbitrary network of constant degree. Suppose
we are given a leveled path collection 7 ~ of size n in G with congestion C,
depth D, and edge buffers of any size q >_ 1. Let K >_ a. C for some constant
a >_ 1. Then Ranade's protocol needs at most O(C + D +
logn)
time steps,
w.h.p., to finish routing in 7 ~.
In case that the degree of G is not a constant then, according to
[LMRR94], the runtime bound needs to be changed to
O(d. 4(l~ -{-
D + logn), w.h.p., where d denotes the maximum degree of G and q again
the buffer size.
The proof of the runtime bound uses a delay sequence argument similar to
the one used for bounding the runtime of the random rank protocol. However,
in contrast to the random rank protocol there are two possible reasons why a
packet may be delayed: It may be delayed either by a packet with lower rank
staying in its current edge buffer, or by q packets with lower ranks occupying
completely the next edge buffer on its way. That these q packets indeed have
lower ranks is ensured by the ghost packets (see the invariant above). Hence

84 7. Oblivious Routing Protocols
we again can construct a sequence of packets with strictly decreasing ranks
that witnesses a long runtime of the protocol. This monotonic behavior of
the ranks can then be exploited to prove a good runtime bound. For more
details see [LMRR94].
7.3.2 Applications
Similar to Theorem 7.2.2 the following result can be shown by using Valiant's
trick.
Theorem 7.3.2. For any wrapped leveled path system of size N (that is,
N input/output nodes) with expected congestion C and depth D there is an
online protocol that routes any h-relation in time O(hC + D + log N), w.h.p.,
using buffers of size two.
This theorem implies the following result together with Lemma 7.2.4.
Theorem 7.3.3. Every h-relation can be routed in a wrap-around butterfly
with N input nodes in time O(h + logN), w.h.p., using buffers of size two.
Ranade [Ra91] also showed that any global permutation can be routed in a
wrap-around butterfly of size N in optimal time O(log N) using only constant
size buffers. This time bound can also be shown for permutation routing in
shuffle-exchange networks [LMRR94]. Furthermore, Ranade's protocol can
be used to route arbitrary d-relations in (n, d)-meshes in optimal time using
only constant size edge buffers [LMRR94].
7.3.3 Limitations
As shown in [LMR94], Ranade's protocol has the following limitation.
Observation 7.3.1. There is an N-node leveled network of degree 3 and a
set of paths with congestion 3 and dilation 3 where the expected runtime of
Ranade's protocol is ~2( ~ ~
log log N ]"
The important point in the proof is that a path collection with congestion
3 and dilation 3 can have a large depth if the sources and destinations of the
packets are not restricted to be at the same level. Hence Ranade's protocol
can only be efficiently applied to path collections that have a dilation that is
approximately the depth of the collection.
7.4 The Growing Rank Protocol
Now we present a protocol that routes packets along an arbitrary shortcut-
free path collection of size n with congestion C and dilation D in O(C + D +
logn) steps, w.h.p., using buffers of size C. It is called growing rank protocol
[MV95] and works as follows.

7.4 The Growing Rank Protocol 85
7.4.1 Description of the Protocol
Initially, each packet is assigned an integer rank chosen randomly, indepen-
dently, and uniformly from [K]. For each step, the protocol works as follows.
For each link with nonempty buffer,
- choose a packet p according to the priority rule,
- increase the rank of p by
K/D,
and
- move p forward along the link.
We generalize the result in [MV95] by analyzing the performance of the grow-
ing rank protocol for the following type of path collections.
Definition 7.4.1.
A path collection 7 9 is called
d-shortcut-free
if any piece
of length at most d of a path in 79 can not be shortcut by any combination of
other pieces of paths in 79.
We can show the following theorem.
Theorem 7.4.1.
Suppose we are given a d-shortcut-~ee path collection 79
of size n with congestion C and dilation D, d < D. Let K > 8C. Then the
growing rank protocol needs at most O(C +
max{l, l~ lD~
d
j j time steps,
w.h.p., to finish routing in 79.
Proof.
Similar to the proof of Theorem 7.2.1 we want to find a structure that
witnesses a long runtime of the growing rank protocol. First we introduce the
following definitions.
In the following, we denote the rank of a packet p while waiting to traverse
a link e by rank e (p). Let id : {set of packets} -+ [n] be an arbitrary bijective
function. We define the
ident-rank
of p at e as rank e (p) + ~ and denote
it by id-rank e (p). Note that in each round the ident-ranks of all packets are
distinct. This type of rank ensures that whenever a packet p delays a packet
p' at a link e it holds id-ranke(p) < id-ranke(p'). The following lemma shows
that the rank of any packet can not be greater than 2K- 1 during the routing.
Lemma 7.4.1.
Suppose p is a packet which is stored in the buffer of link e
in some round. Then
ranke(p) _ 2K - 1.
Proof.
At the beginning, the rank of p is at most K - 1. Since the length of
the routing path of p is at most D, the rank of p is increased by D K- for at
most D times. Thus, rank e (p) < K - 1 + D. K < 2K - 1. []
Analogous to the proof for the random rank protocol, the following de-
lay sequence will serve as a witness for a long runtime of the growing rank
protocol.
Definition 7.4.2 ((s, s K)-delay sequence).
An (s, ~,
K)-delay sequence
consists of

86 7. Oblivious Routing Protocols
1. s not necessarily distinct delay links el,..., es;
2. s + 1 delay packets Pl,P2, . . . ,Ps+l such that the path of pi moves along
the link ei and the link ei-1 in that order for all i E {2,..., s}, the path
of ps+l contains es, and the path of pl contains el;
3. s integers ~1,~2,...,~s > 0 such that ~1 is the number of links on the
routing path of packet Pl from el (inclusive) to its destination, for all
i E {2,..., s} gi is the number of links on the routing path of packet Pi
from link ei (inclusive) to link el-1 (exclusive), and ~-~i~=1 gi < ~; and
4. s integer keys rl,r2,...,rs+l such that 0 <_ rs+l <_ "" <_ r2 <_ rl < 2K.
We call s the length of the delay sequence. Further we say that a delay se-
quence is active, /f rank e' (pi) = ri for all i E {1,..., s} and rank e" (Ps+l) =
rs+l
Lemma 7.4.2. Suppose the routing takes T > 2D or more rounds. Then
there exists an active (T - 2D, 2D, K)-delay sequence.
Proof. First, we give a construction scheme for a delay sequence. Let pl be a
packet that arrived at its destination Vl in step T. We follow Pl's routing path
backwards to the last link on this path where it was delayed. We call this link
el, and the length of the path from v to el (inclusive) ~1. Let P2 be the packet
that caused the delay, since it was preferred against Pl. We now follow the
path of p2 backwards until we reach a link e2 at which P2 was forced to wait,
because the packet pa was preferred. Let us call the length of the path from
el (exclusive) to e2 (inclusive) e2. We change the packet again and follow the
path of P3 backwards. We can continue this construction until we arrive at a
packet ps+l that prevented the packet Ps at edge es from moving forward.
The path from es to Vl recorded by this process in reverse order is called
delay path. It consists of contiguous parts of routing paths. In particular, the
part of the delay path from link ei (inclusive) to link ei-1 (exclusive) is a
subpath of the routing path of packet Pi.
Let ri = rankei(pi) for all 1 < i < s and rs+l = ranke" (Ps+l). Because of
the contention resolution rule we have 0 < rs+l < ... < rl, and rl < 2K - 1
because of Lemma 7.4.1. Thus, we have constructed an active (s, s K)-delay
sequence for every g > ~-~f=x ei.
Our next goal is to bound the sum of the gi's. In addition to the ranks
rl,..., r8+1, we denote by ro the rank of Pl at its destination. It follows
immediately from the protocol that ri + s 9 K < ri-1 for all 1 < i < s. As a
consequence,
s K
Letup7.4.1 s
D
gi "~ < r0 ~ei < (2K- 1).~ < 2D . (7.1)
i----1 i=1
Since the delay sequence consists of ~-'~i8=1 ei moves and s delays, it covers
8
at most t = ~-~i=l e~ + s time steps. It follows that

7.4 The Growing Rank Protocol 87
8 (7.1)
t=~-~i+s < 2D+s.
i=1
Consequently, if we stop the above construction at packet
PT-2D+I,
we still
have t < T and therefore found an active (T- 2D, 2D, K)-delay sequence. [3
Instead of considering the whole delay sequence, we will only consider a piece
of it that is chosen in such a way that we can be sure that no packet can
appear twice in it. For this we introduce the following definition.
Definition
7.4.3
((s', s
K')-delay subsequence).
An (s',~',
K')-delay
subsequence
consists of
1. s' not necessarily distinct
delay links el,...,
e,,;
2. s' + 1 delay packets
pl,P2,... ,p8,+1 such that the path of pi moves along
the link e{ and the link ei-1 in that order for all i E
{2,..., s'},
the path
of ps,+l contains es,, and the path of pl contains el;
3. s' integers
~1,~2,.-.,~s, _> 0
such that ~ is the number of links on the
routing path of packet p{ from link e{ (inclusive) to link ei-1 (exclusive)
8 t
for all i e
{2,..., s'},
and ~i=2 s <_ s and
4. s' integer keys
rl,r2,...,rs,+l
such that O <
rs,+l _< ... _< r2 _< rl <
rs,+l + 2K' and rl < 2K.
We say that a delay subsequence is
active,
if ranke'(pi) = ri for all i E
{1,..., s'}
and
rank e'' (P8,+1) =
rs,+l
The following lemma will be helpful to bound the total delay, length, and
delay range of a subsequence of a delay sequence. Its proof is similar to a
proof in [LMRR94] (see Lemma 2.10).
Lemma 7.4.3.
If there exists an active (s, ~, K)-delay sequence, then there
exists an active ( ~, ~-~, ~ )-delay subsequence for every a > 1.
Proof.
Suppose that an (s, t, K)-delay sequence is active. Divide the packet
sequence p2,...
,ps+l
into a contiguous subsequences such that each subse-
quence has at least
Ls/aJ > s/2a
packets. This also partitions the delay path
into subpaths. Let subsequence 0 consist only of packet pl. For every subse-
quence i > 1, let ti denote the length of the ith subpath and let 2Ki denote
the delay range of ranks for the ith subsequence, i.e., 2Ki is the difference
between the rank of the last packet in subsequence i - 1 when delayed by the
first packet in subsequence i, and the rank of the last packet in subsequence
i when delaying the second last. We know that there must be fewer than
a/2
segments with K~ >
2K/a,
since ~ 2Ki < 2K. Furthermore there must be
fewer than
a/2
segments satisfying ti >
2~/a,
since ][: ~i < t- Thus there
must exist some segment for which ~ <
2t/a and Ki <_ 2K/a. 0
2K
Next we show that, if we restrict -5- to be at most d. D, then no packet can
appear twice in a (2-~,s 2~_, ~)_delay subsequence.

88 7. Oblivious Routing Protocols
Lemma 7.4.4.
For any (s',~',K')-delay subsequence with K' <_ d . D it
holds that no packet can appear twice in it.
Proof.
Suppose, in contrast to our claim, that there is some packet p ap-
pearing twice in an (s', g', K')-delay sequence. Then there exist i and j with
1 _< i < j _< s' + 1 and p =
Pi
= Pj. Thus, the routing path of p crosses the
delay path at the delay links ej-1 and
ei
in that order. Since the rank of a
packet is increased by -~ each time it traverses an edge and the range of the
ranks is bounded by d. D, the length of the path the packet p traverses from
ej-1 (inclusive) to
ei
(exclusive) can be at most d. Let m denote the distance
from link ej-t (inclusive) to link
ei
(exclusive) in the delay path. Since the
routing paths are d-shortcut-free, the rank of p is increased at most m times
while moving from
ej_l
to
el,
and hence,
K
id-rank e' (p) _< id-rank e~-I (p) + m. ~ . (7.2)
On the other hand, since for every k E {1,...,s'} packet
Pk+l
delays
packet Pk at edge
ek,
we have id-ranke~(pk) > id-ranke~(pk+l) for all k E
{1,..., s'}. Further, the length of the routing path of packet Pk+l from
ek+l
to
ek
is ~k+t, and thus the rank of
Pk+l
is increased by ~k+l 9 D g- on its path
from
ek+l
to ek
for all k E {1,...,s'- 1}. It follows that id-rank e~ (Pk) >
id-rank ek+l (Pk+l) +/k+l " ~ for all k E {1,..., s' - 1}. This yields
j-1 K
id-ranke'(P) > id-rankeJ-l(P) + Z ~k"
k=i+l
K
= id-rank ej-l(p) + m. ~ . (7.3)
Since (7.3) contradicts (7.2), there is no packet that appears twice in the
delay subsequence. []
Our goal is therefore to restrict the range of the ranks used in the delay
subsequence to be considered to at most d. D. First we count the number of
ways to construct an (s', ~', K')-delay subsequence.
Lemma 7.4.5.
The number of different (s', g', K')-delay subsequences is at
most
s' \ s'+l ] "
Proof.
There are n packets from which Pt can be chosen, and at most D
possibilities to choose gl. Furthermore there are at most [ e'+s'~ possibilities
~, st !
to choose the gi such that ~-]~i~2 ti _< ~'. Since Pt and gt determine the link
el and the congestion at el is at most C, there are at most C possibilities to
choose packet P2. The same holds for the packets p3,... ,Ps,+l at the edges
e2,
es,.
Hence we altogether have at most
n . D 9 (t' +st~ 9 C s'
possibilities
9 . . , ~, s ~ ]
