Сборник докладов - Электроэнергетика глазами молодежи 2010

Подождите немного. Документ загружается.

275

наглядное представление результатов и не требует поддержания отдельной модели, свя-

занной с представлением схемы как однолинейной электрической.

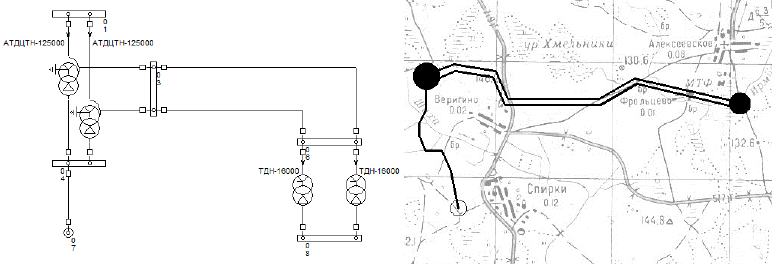
В рамках комплекса EnergyCS поддерживается карта-схема (рисунок 1). Наличие

объектов на карте-схеме отмечено непосредственно в информационной модели. Отобра-

жение карты-схемы реализовано с помощью системы AutoCAD, интегрированной с

EnergyCS на уровне СОМ-сервера. Элементы схемы, ключевые для построения карты

схемы (узлы подстанций, линии), передаются в виде условных графических изображений

в AutoCAD, становясь при этом особыми объектами. Объекты могут быть привязаны к

карте местности. Карта местности в AutoCAD может быть загружена как в виде векторной

модели местности, так и в виде растровой подложки, полученной путем сканирования, к

которой привязываются элементы сети. При этом связь между объектами EnergyCS и Au-

toCAD в процессе работы обеспечивается как в едином приложении.

Рисунок 1 – Модель и карта-схема сети

Объединение свойств нескольких моделей в одну основано на применении объект-

ного подхода к формированию модели, когда модель сети представляется совокупностью

взаимосвязанных объектов с набором всех свойств, необходимых для формирования соот-

ветствующих расчетных схем. То есть можно говорить об информационной модели, на

основе которой сформирована математическая, соответствующая решаемой задаче.

Каждый объект обладает набором свойств и параметров:

 топологических, т. е. определяющих его положение на схеме;

 схемных и режимных, использующихся при выполнении расчетов;

 графических, т.е. отвечающих за визуальное отображение объекта на электриче-

ской однолинейной схеме, схеме замещения и карте-схеме.

Один и тот же объект может отображаться по-разному.

При таком подходе ввод модели сводится к вводу отдельных объектов и заданию

их схемных параметров при помощи базы данных справочника-каталога паспортной ин-

формации. Например, для линии задается ее тип, длина участка, конструкция фазы, нали-

чие расщепления фазы, марка провода, возможно, тип опоры. Для трансформатора задает-

ся тип, а так же режим работы нейтрали в обмотке звезда и номер отпайки РПН.

Информационная модель, получающаяся в итоге, является качественно новым объ-

ектом: она объединяет свойства исходных моделей, а также является базой данных сети и

платформой для дальнейших исследований. В частности, доступ и к результатам расчета

режима, и к справочной базе оборудования дает возможность для решения новых задач,

выбора оборудования, оптимизации, технико-экономического сравнения.

Часто для формирования модели или решения каких-либо специфичных задач не-

обходимо обращение к сторонним программам. Поскольку адаптация моделей сторонних

программ под информационную модель, созданную в программном комплексе EnergyCS,

невозможна, решением является использование универсального формата обмена. С точки

зрения технической реализации перспективно строить обменный формат на основе XML,

поскольку этот способ описания данных стал наиболее популярен в разных приложениях

276

общего назначения и в связи с тем, что системы синтаксического разбора для него входят

непосредственно в состав современных операционных систем.

Реализация формата обмена на основе XML предполагает разработку специализи-

рованного подмножества XML, предназначенного для описания моделей электроэнерге-

тических систем. Вариант такого решения приведен в стандарте МЭК 61970, где предло-

жена модель CIM (Common Information Model). Данный стандарт был разработан для уп-

рощения интеграции приложений и систем управления энергетикой, разработанных неза-

висимо друг от друга разными производителями. В программном комплексе EnergyCS

сделана попытка реализовать этот стандарт обмена. Одновременно осуществлен и обмен

данными с использованием XML, реализующий внутреннюю структуру данных EnergyCS,

которая документирована и более проста в реализации, чем CIM XML.

Особой задачей при создании моделей стало применение и обработка программой

сложных распределительных устройств. Интерес к этой задаче объясняется потребностью

наиболее полно и гибко отражать влияние работы распределительного устройства на оп-

ределение режимных параметров, получать токи, протекающие через выключатели, а так-

же максимально приблизить графическое отображение модели к электрической одноли-

нейной схеме.

Отражение выключателя в модели производится с помощью двух механизмов:

1) вспомогательный элемент каждого объекта – маркер-выключатель, позволяющий вре-

менно вывести ветвь из расчетной модели, «отключить» ее; 2) специальная ветвь-выключатель.

Ветвь-выключатель моделируется гибкой комбинацией двух подходов. Первый

подход: выключатель рассматривается моделью как ветвь с малым сопротивлением по-

рядка 0,001 Ом. При таком моделировании можно получать любые схемы РУ. Выключа-

тели обрабатываются так же, как и все остальные ветви. Они учитываются в матрице уз-

ловых проводимостей, а число узлов на расчетной схеме соответствует числу узлов в ин-

формационной модели. Этот подход удобен тем, что не требует особой пострасчетной об-

работки, а результаты получаются так же, как результаты для всех остальных ветвей. Од-

нако при таком подходе существенно ухудшается сходимость итерационного расчета

вследствие ухудшения обусловленности матрицы коэффициентов системы уравнений.

Второй подход представляет ветвь-выключатель как фиктивную ветвь, которая исключа-

ется из расчетной схемы перед процедурой расчета, объединяя узлы информационной мо-

дели, связанные выключателями, в один узел расчетной схемы. Таким образом, всё РУ

сводится к одному узлу. В пострасчетной обработке узлы восстанавливаются.

Предлагается следующий алгоритм: на этапе построения расчетной модели иден-

тифицируются узлы, входящие в РУ (узлы, к которым подключены ветви-выключатели).

Они объединяются в кластеры. При формировании уравнений установившегося режима

ветви-выключатели и узлы-кластеры, кроме опорного узла,

не учитываются. Мощности,

заданные в узлах, передаются опорному узлу путем алгебраического суммирования. Та-

ким образом, весь кластер представлен в модели одним узлом. После расчета установив-

шегося режима узлам кластера присваиваются расчетные напряжения опорного узла и оп-

ределяются токи во всех ветвях схемы. Далее для каждого кластера выполняется решение

системы линейных уравнений

для определения отклонений напряжения в узлах кластера от

напряжения опорного узла, вызванного токораспределением по ветвям-выключателям РУ:





,

∆







,б

, (1)

где 



,

– матрица собственных и взаимных проводимостей; 



,б

– матрица-столбец за-

дающих токов, определенных по результату расчета установившегося режима; ∆



– мат-

рица-столбец разностей напряжений по отношению к опорному узлу. Полученные урав-

нения являются линейными и не требуют итерационного расчета. Поэтому проблема схо-

димости, связанная с плохой обусловленностью матрицы коэффициентов, отсутствует.

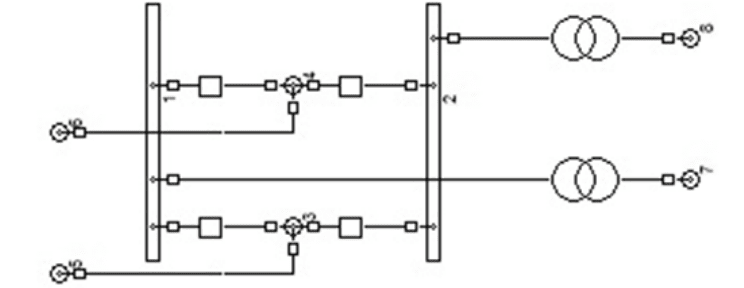
277

Рисунок 2 – Моделирование сложного распределительного устройства

Матрица коэффициентов уравнений (матрица узловых проводимостей) формирует-

ся из узлов, входящих в кластеры, в том числе и опорных. В этой матрице ветви-

выключатели представляются ветвями с малым сопротивлением, правые части являются

алгебраическими суммами токов ветвей, подключенных к узлам, входящих в кластеры и

собственных токов инъекций этих узлов. По найденным в результате решения этих урав-

нений отклонениям напряжений в узлах кластеров рассчитывается токораспределение в

ветвях-выключателях РУ.

Особым вопросом составления информационной модели сети является моделиро-

вание распределительных сетей 6–10 кВ. Как правило, эти сети являются разомкнутыми, а

наличие в расчетной модели разомкнутых сетей ухудшает сходимость итерационного

процесса расчета режима. При этом расчет разомкнутых сетей может быть проведен более

простым топологическим методом по данным о нагрузке и напряжениях в начале участков

разомкнутых сетей.

Программа EnergyCS позволяет сочетать в расчетной модели участки сетей, ре-

жимные параметры которых рассчитываются по методу узловых напряжений и участки,

которые рассчитываются топологическим методом при использовании фидеров. Под фи-

дером в программе EnergyCS понимается участок разомкнутой распределительной сети,

отходящий от каких-либо шин и получающий питание от этих шин. Эти участки могут

состоять из линий электропередачи, трансформаторов, нагрузок, ТП и КТП. Необходимо

отметить, что общая информационная модель сети не отличается для замкнутых и ра-

зомкнутых участков, различия имеют место только при расчете.

Таким образом, расчет режима разбивается на три этапа. Первый этап состоит в

определении токов, перетоков мощности, напряжений в распределительных сетях по фи-

дерам. Итогом этого расчета будут нагрузки для узлов, определенных для фидеров. Вто-

рой этап – расчет установившегося режима во внешней для фидера сложнозамкнутой се-

ти. Третий этап связан с уточнением напряжений в узлах фидеров после уточнения расче-

та установившегося режима.

В заключение следует отметить основные выводы по работе:

1. Информационная модель позволяет объединить множество моделей для реше-

ния разных задач и сократить ошибки при проектировании. Реализована в EnergyCS.

2. Применение форматов обмена на основе XML позволяют интегрировать в еди-

ную систему программные продукты разных разработчиков.

3. Предложенные алгоритмы учета выключателей позволяют включать схемы РУ в

модели, как для расчетов установившихся режимов, так и для расчетов ТКЗ, без ущерба

для сходимости и точности.

4. Моделирование разомкнутых участков сети в единой модели позволяет сокра-

тить размерность системы уравнений при расчете установившихся режимов и одновре-

менно применить специфические алгоримы расчета таких участков.

278

РАНГОВЫЙ АНАЛИЗ КАК МЕТОД ИССЛЕДОВАНИЯ БОЛЬШИХ

ТЕХНИЧЕСКИХ СИСТЕМ ОСОБОГО ЦЕНОЛОГИЧЕСКОГО ТИПА

Е.Ю. Сизганова, С.Ф. Лукьяненко

СФУ

Специфика техноценозов проявляется, в том числе, в методологических основани-

ях их исследования. Техноценозы не поддаются описанию ни традиционными методами

гауссовой математической статистики, оперирующей понятиями среднего и дисперсии

как информативно насыщенными свертками больших массивов статистической информа-

ции, ни лежащими в основе редукционизма имитационными моделями. Чтобы корректно

описать техноценоз, необходимо постоянно оперировать выборкой в целом, как бы велика

она ни была, что предполагает построение видовых и ранговых распределений, теоретиче-

ская основа которых лежит в области негауссовой (ципфовой) математической статистики

устойчивых гиперболических безгранично делимых распределений [1, 2, 3]. Методология

построения видовых и ранговых распределений, а также их последующего использования

в целях оптимизации техноценоза составляет основной смысл рангового анализа, содер-

жание и технология которого представляют собой новое фундаментальное научное на-

правление, сулящее большие практические результаты.

Ранговый анализ – метод исследования больших технических систем особого цено-

логического типа (техноценозов), имеющий целью их статистический анализ, а также оп-

тимизацию, и полагающий в качестве основного критерия форму видовых и ранговых

распределений. Включает стандартные процедуры параметрического нормирования, ин-

тервального оценивания, прогнозирования и нормирования потребления ресурсов. Более

тонкий анализ ранговых параметрических распределений позволяет существенно повы-

сить эффективность рангового анализа. Он осуществляется в рамках следующих (так на-

зываемых «тонких») процедур: дифлекс-анализа (на этапе интервального оценивания),

GZ-анализа (на этапе прогнозирования) и ASR-анализа (на этапе нормирования) [4, 1].

Рассмотрим ключевые понятия, математические основы и содержание рангового

анализа. Первым исходным моментом в методологии рангового анализа является понятие

распределения. В самом общем случае распределение – это расположение элементов под-

множества внутри множества [8, 9, 10]. В математике рассматриваются статистические и

вероятностные распределения. Как правило, на практике исследователь начинает работу с

построения статистического распределения, которое возникает при эмпирическом описа-

нии выборки конечного объема из генеральной совокупности. Следовательно, оно дис-

кретно на множестве значений случайной величины. Как идеализация статистического

распределения в ситуации, когда объем выборки из генеральной совокупности стремится

к бесконечности, возникает вероятностное распределение, которое в общем случае явля-

ется непрерывным на множестве значений случайной величины [1, 5].

Вторым ключевым моментом является понятие случайной величины, которое бази-

руется на общем представлении о таком понятии, как «случайность». В современной ли-

тературе обычно различают семь причин случайности: 1) непонятая закономерность; 2)

скрещение несогласованных процессов; 3) уникальность; 4) неустойчивость движения;

5) относительность знания; 6) имманентная случайность; 7) произвольный выбор [6, 7].

Нам представляется, что при исследовании объектов техноценологического типа мы, в той

или иной степени, имеем дело с причинами пятого и седьмого типов. Во-первых, насыще-

ние техноценозов изделиями-особями происходит в условиях одновременного воздейст-

вия огромного количества слабосогласованных внешних и внутренних факторов, что де-

лает случайной его номенклатуру или видовую структуру. Также доказано, что видообра-

зование в техноценозе фрактально, а его границы размыты, конвенционны. Кроме того,

279

техноценоз постоянно изменяется во времени, причем это изменение векторизовано и не-

обратимо (однонаправленно). Следовательно, можно говорить, что в данный фиксирован-

ный момент времени номенклатура техноценоза является случайной. И если описать но-

менклатуру частотным распределением, то форма последнего будет случайной (его пара-

метры будут случайными величинами). Очевидно, здесь мы имеем дело в полном смысле

этого слова с проявлением трансцендентности техноценозов [11, 14–18], делающей наши

знания относительными, что является фундаментальной причиной случайности пятого

типа.

Во-вторых, совокупность параметров, описывающих особи техноценоза, составля-

ет двумерное пространство. Оба измерения данного пространства бесконечны, однако,

одно из них (перечисляющее особи техноценоза) счетно, а второе (описывающее парамет-

ры) – континуально. Это является следствием другого известного свойства техноценозов,

а именно того, что число особей в них бесконечно (точнее – математически счетно)

[11, 14–18]. Кроме того, общее параметрическое пространство делится на два равномощ-

ных подпространства: видообразующих и функциональных параметров. В любом случае,

если осуществлять произвольный выбор особей техноценоза, то параметры выбранных

технических изделий составят статистическую выборку случайных величин. Если учесть,

что техноценоз трансцендентен, то выбор особей при этом может осуществляться как

угодно. Очевидно, что любой выбор из трансцендентной бесконечности будет произволь-

ным и, по сути, случайным. Здесь мы констатируем причину случайности седьмого типа

(произвольный выбор). Если полученную выборку обрабатывать методами математиче-

ской статистики, то можно получить параметрическое распределение.

Таким образом, случайным в широком смысле является сочетание (именно фикси-

рованное сочетание) видов технических изделий, составляющих техноценоз, если мы его

рассматриваем среди большого количества других подобных техноценозов. Судить о ста-

тистическом (и далее – вероятностном) распределении данных сочетаний можно лишь

полномасштабно исследовав поведение техноценозов в более общем таксономическом

образовании – метаценозе (доступной для исследования в данный момент времени сово-

купности техноценозов). В узком смысле случайной является форма видового распреде-

ления, описывающего номенклатуру техноценоза, что делает случайной величиной значе-

ние соответствующего формального параметра. С другой стороны, если рассматривать

совокупность одноименных параметров технических изделий (особей) отдельного техно-

ценоза как выборку из параметрического пространства, то значение фиксированного па-

раметра конкретного технического изделия может рассматриваться как случайная величи-

на, а саму выборку можно описать как статистическое распределение.

В этом смысле следует подчеркнуть принципиальную разницу между видовыми и

ранговыми распределениями техноценоза. Его видовые распределения случайны, потому

что случайны макроскопические параметры их формы. Ранговые же распределения – это

распределения случайных величин (параметров, характеризующих особи). Именно в этом

контексте мы и применяем к техноценозам понятие статистического распределения. По-

следующее особое обобщение на континууме техноценоза (его особенность будет показа-

на ниже) позволяет получать распределение, имеющее смысл вероятностного.

Третьим ключевым моментом в методологии рангового анализа являются понятия

негауссовости и ципфовости описывающих

техноценозы гиперболических распределений.

Как всегда, начнем с устоявшихся определений. Вероятностное распределение мы назы-

ваем гауссовым, если для него выполняется центральная предельная теорема, т.е. при ши-

роких предположениях относительно законов распределения независимых случайных ве-

личин с ростом числа слагаемых закон распределения суммы этих величин неограниченно

приближается к нормальному. Статистическое распределение называется гауссовым, если

зависимость его среднего и дисперсии от объема выборки несущественна, т.е. в условиях

280

данной конкретной исследовательской задачи выполняется закон больших чисел (при

достаточно большом числе независимых испытаний среднее арифметическое наблюден-

ных значений случайной величины сходится по вероятности к ее математическому ожи-

данию) [5]. Очевидно, что, в общем случае, любое распределение, для которого не выпол-

няется хотя бы одно из приведенных выше двух условий, является негауссовым.

Ципфовым принято называть распределение, имеющее при больших значениях пе-

ременной вид распределения Ципфа.

Теперь мы готовы повторить точные определения, распространяющие ципфовую

методологию на прикладную область рангового анализа. Под видовым понимается рас-

пределение Ципфа в частотной дифференциальной форме, устанавливающее непрерыв-

ную или дискретную упорядоченную взаимосвязь между множеством значений возмож-

ной численности особей техноценоза и количеством популяций, реально представленных

в техноценозе данной фиксированной численностью. По сути, видовое распределение ус-

танавливает основополагающую взаимосвязь между массовостью изделий различных ви-

дов в техноценозе и их разнообразием. Математически оно относится к гиперболическим

устойчивым безгранично делимым распределениям [11, 2].

Под ранговым распределением вообще понимается убывающая последователь-

ность значений параметров, упорядоченная таким образом, что каждое последующее чис-

ло меньше предыдущего, и поставленная в соответствие рангу (номеру по порядку в дан-

ной упорядоченной последовательности). Таким образом, неотъемлемой чертой рангового

распределения является целенаправленное ранжирование входящих в него параметров ви-

дов, объектов или особей техноценоза. В этом его принципиальное отличие от видового

распределения, где подобная операция не предусмотрена.

Ранговое распределение техноценоза – полученное в результате процедуры ранжи-

рования видов или особей техноценоза по какому-либо параметру распределение Ципфа в

ранговой дифференциальной форме, по сути являющееся невозрастающей последователь-

ностью значений самих параметров, поставленных в соответствие рангу. Различают ран-

говые распределения, в которых ранжируются: виды по количеству особей, которым они

представлены в техноценозе (ранговые видовые); особи по значению видообразующего

параметра (ранговые параметрические); особи (объекты) по значению параметра, характе-

ризующего их функционирование (ранговые функциональные) [11, 12].

Практическая реализация рангового анализа, как правило, состоит в осуществлении

следующих комплексных этапов-процедур [13]:

1. Выделение техноценоза.

2. Определение перечня видов в техноценозе.

3. Задание видообразующих параметров.

4. Параметрическое описание техноценоза.

5. Построение табулированного рангового распределения.

6. Построение графического рангового видового распределения.

7. Построение графических ранговых параметрических распределений.

8. Построение видового распределения.

9. Аппроксимация распределений.

10. Оптимизация техноценоза.

Вывод: Таким образом, ранговый анализ представляет собой метод исследования

больших технических систем особого ценологического типа (техноценозов), имеющий

целью их статистический анализ, а также оптимизацию, и полагающий в качестве основ-

ного критерия форму видовых и ранговых распределений.

281

Список использованных источников

1. Гнатюк В.И. Закон оптимального построения техноценозов. – Выпуск 29. Ценологи-

ческие исследования. М.: Изд-во ТГУ – Центр системных исследований, 2005. 384 с.

2. Кудрин Б.И. Введение в технетику. Томск: Изд-во ТГУ, 1993. 552 с.

3. Кудрин Б.И., Крылов Ю.К. Целочисленное аппроксимирование ранговых распределе-

ний и идентификация техноценозов. Выпуск 11. Ценологические исследования. М.:

Центр системных исследований, 1999. 79 с.

4. Гнатюк В.И. Лекции о технике, техноценозах и техноэволюции. Калининград: КВИ

ФПС РФ, 1999. 84 с.

5. Хайтун С.Д. Проблемы количественного анализа науки. – М.: Наука, 1989. 280 с.

6. Чайковский Ю.В. Элементы эволюционной диатропики. – М.: Наука, 1990. 272 с.

7. Чайковский Ю.В. О природе случайности. – Выпуск 18. Ценологические исследова-

ния. – М.: Центр системных исследований, 2001. 279 с.

8. Айвазян С.А. и др. Прикладная статистика: Классификация и снижение размерности.

М.: Финансы и статистика, 1989. 607 с.

9. Корн Г., Корн Т. Справочник по математике. М.: Наука, 1978. 832 с.

10. Королюк В.С., Портенко Н.И., Скороход А.В. и др. Справочник по теории вероятно-

стей и математической статистике. М.: Наука, 1985. 640 с.

11. Гнатюк В.И. Оптимальное построение техноценозов. Теория и практика. Выпуск 9.

Ценологические исследования. М.: Центр системных исследований, 1999. 272 с.

12. Гнатюк В.И., Лагуткин О.Е. Ранговый анализ техноценозов. Калининград: БНЦ РАЕН

– КВИ ФПС РФ, 2000. 86 с.

13. Гнатюк В.И. Закон оптимального построения техноценозов. – Выпуск 29. Ценологи-

ческие исследования. М.: Изд-во ТГУ – Центр системных исследований, 2005. 384 с.

14. Кудрин Б.И. Зачем технарию Платон. М.: Электрика, 1996. 216 с.

15. Кудрин Б.И., Федяев Д.М. Техническая реальность в ХХI веке. Материалы к круглому

столу Всероссийской научной конференции (Омск, 21 – 22 января 1999 г.). Омск: Из-

дание Омского ГПУ, 1999. 68 с.

16. Кудрин Б.И. Технетика: новая парадигма философии техники (третья научная картина

мира). – Томск: Изд-во ТГУ, 1998. 40 с.

17. Кудрин Б.И. Античность. Символизм. Технетика. М.: Электрика, 1995. 120 с.

18. Кудрин Б.И. Символизм и основы технетики (становление неклассического мышле-

ния). Томск: Изд-во ТГУ, 1993. 43 с.

282

РАСПРЕДЕЛЕННАЯ ГЕНЕРАЦИЯ, ПЕРСПЕКТИВЫ

И НАУЧНЫЕ ПРОБЛЕМЫ

А.А. Карпенко, А.В. Паздерин

УрФУ

Введение. На протяжении многих десятилетий, вплоть до конца XX века, мировая

энергетика развивалась по пути повышения концентрации и увеличения единичных мощ-

ностей. В целях повышения КПД увеличивались мощности энергетических установок, по-

вышались уровни номинального напряжения электрических сетей. За эти годы были соз-

даны большие электроэнергетические системы (ЭЭС), покрывающие своей сетью огром-

ные территории. Для обеспечения работы единых ЭЭС создавались многоуровневые ие-

рархические системы диспетчерского управления, которые позволяли управлять режима-

ми работы, повышать надежность и экономичность ЭЭС. Централизованный путь разви-

тия энергетики привел к возникновению энергетических корпораций, монопольно обеспе-

чивающих энергоснабжение потребителей на своей территории и совмещающих все ос-

новные виды энергетического бизнеса: выработку, транспорт, продажу (сбыт) энергии,

диспетчеризацию, ремонты, техобслуживание и другие вспомогательные услуги.

Либерализация электроэнергетики, распространившаяся в конце XX века практи-

чески повсеместно, привела отрасль к конкуренции. В немалой степени этому процессу

способствовало развитие новых энергетических технологий, связанных со снижением

единичных мощностей энергоустановок и получивших название «распределенная генера-

ция» (РГ). Новый уровень развития технологий позволяет рассматривать РГ как альтерна-

тивный по отношению к централизованной энергетике путь обеспечения потребителей

электрической энергией.

Определение распределенной генерации. РГ это принципиально новое явление в

энергетике. Вследствие этого, как показал анализ литературы по данной проблеме, для

этого термина общепринятое определение пока отсутствует. В зарубежной литературе для

понятия «распределенная генерация» используется различная терминология. Например, в

Австралии часто используют термин «встроенная генерация», в странах Северной Амери-

ки – термин «рассредоточенная генерация», в Европе и некоторых азиатских странах –

«децентрализованная генерация» [1]. Помимо терминологии существенно отличается и

классификация устройств РГ, в частности классификация по установленной мощности. На

международном уровне эти различия обусловлены особенностями политического и эко-

номического устройства государств.

В некоторых странах определение РГ основывается на классах напряжений. Но, как

известно, в разных странах существуют отличия классов напряжений для передающей и

распределительной сетей, что также создает барьер для четкой формулировки понятия

малой генерации. В зарубежных источниках рассуждения ведутся с позиций, что РГ под-

ключается к электрическим сетям, питающим нагрузку напрямую. Также определение РГ

зачастую дается исходя из присущих данным устройствам свойств (например, использо-

вание возобновляемых источников энергии, возможность когенерационной работы, отсут-

ствие диспетчерского контроля над агрегатами).

Приведем несколько определений, предложенных различными организациями, на-

учными сообществами и отдельными учеными.

Институт инженеров по электротехнике и электронике (IEEE) определяет

РГ как

генерацию электрической энергии при помощи агрегатов, значительно меньших по мощ-

ности, нежели централизованные электрические станции, что позволяет реализовать под-

ключение данных энергоустановок практически к любой точке энергосистемы.

283

Международный Совет по большим Энергетическим Системам (CIGRE) определя-

ет РГ как любую генерацию с максимальной установленной мощностью от 50 до 100 МВт,

которая подключается к распределительным сетям и не подвергается централизованному

планированию и диспетчеризации.

Донди и др. [2] определяют РГ как малый источник электрической энергии или

устройство для ее запасания (мощностью от нескольких ватт до десятков мегаватт), кото-

рые не являются частью большой централизованной энергосистемы и расположены вбли-

зи от места потребления. Здесь авторы включают в определение возможность запасания

электрической энергии, что является достаточно нетипичным.

Акерман и др. [1] дают определение устройствам РГ с точки зрения мест присоеди-

нения РГ к сети и расположения, а не с позиции количественной оценки установленной

мощности. Авторы определяют РГ как генерирующие установки, подключенные напря-

мую к распределительной сети или установленные с потребительской стороны от границы

балансовой принадлежности.

Последнее определение является наиболее общим, поскольку оно не накладывает

ограничений на технологии и установленную мощность потенциально используемых ус-

тановок РГ, поэтому в данной статье оно будет принято в качестве вводного.

Область применения распределенной генерации. На сегодняшний день РГ ши-

роко используется потребителями для обеспечения их электроэнергетических нужд. На-

пример, для снижения стоимости счетов за электрическую энергию, покупаемую у элек-

троснабжающей организации, для применения в качестве единственного источника мощ-

ности, либо в целях охраны окружающей среды. РГ также может быть использована энер-

гокомпаниями для решения определенных эксплуатационных задач. Существует много

других способов применения устройств РГ, основные из которых:

 постоянное (непрерывное) электроснабжение;

 совместная выработка тепла и мощности (когенерация);.

 работа в пиковые часы;

 экологически чистое производство электрической энергии;

 электроснабжение при наличии жестких требований к надежности и качеству;

 отсрочка модернизации передающей и транспортной сети;

 вспомогательные услуги по электроснабжению.

Научные проблемы распределенной генерации. Теперь обратимся к научным

проблемам, связанным с РГ, которые обуславливают основные направления исследований

в этой области. Они близки к традиционной проблематике больших электроэнергетиче-

ских систем. Однако количественные отличия часто

переходят в качественные, что требу-

ет изучения свойств и особенностей систем с источниками РГ. Можно выделить следую-

щие основные направления научных исследований.

 Математические и оптимизационные модели для выбора мощности и располо-

жения различных типов объектов РГ. Расположение устройств РГ может значительно

влиять на систему [3]. В случае если расположение и

мощность устройства РГ не были

выбраны должным образом, может возникнуть ряд режимных проблем, включая повыше-

ние напряжения в конце фидера, возникновение небаланса генерации и нагрузки при ава-

рии, увеличение потерь электрической энергии и снижение надежности [4]. В то же время

корректно выбранная точка подключения РГ к сети может способствовать улучшению

технико-экономических и эксплуатационных параметров.

Для решения данной задачи используются самые разнообразные оптимизационные

методики – от хорошо известных традиционных алгоритмов, включающих в себя методы

284

нелинейного, квадратичного программирования, методы градиента, до эвристических ал-

горитмов, имитирующих эволюционные и прочие природные процессы.

Оптимизационные алгоритмы позволяют учитывать технические критерии сниже-

ния потерь электрической мощности, улучшения параметров напряжения, повышения по-

казателей надежности электроснабжения, а также экономические, включающие в себя

снижение стоимости покупаемой потребителями электрической энергии, ограниченность

инвестиционных ресурсов и другие.

 Регулирование уровней напряжения и реактивной мощности за счет устройств

РГ, располагающихся вблизи потребителей, существенно повышает управляемость реак-

тивной мощностью и напряжениями за счет возможности осуществления динамичной

инъекции реактивной мощности в сеть. Таким образом, появляется возможность значи-

тельного увеличения показателя стабильности напряжения.

Стабильность напряжения – это способность энергосистемы поддерживать напря-

жения установившегося режима во всех узлах после нарушения заданных первоначальных

эксплуатационных условий системы [5]. Несмотря на то, что нестабильность напряжения

– локальное явление, данный вопрос актуален для всей энергосистемы и особенно важен

для эксплуатации и управления сильно нагруженными сетями, сетями с недостатком реак-

тивной мощности и часто возникающими нарушениями нормальной работы.

 Реконфигурация распределительных сетей, содержащих источники РГ, формиру-

ет еще одно направление исследований. С ростом числа и мощности синхронных генера-

торов перераспределяются потоки мощности в сети, а также увеличиваются токи КЗ. По-

этому на стадии принятия решения о строительстве мини-станции необходимо выполнить

предпроектное обследование по выбору мест заземления нейтрали и нормальных разры-

вов в сети, что особенно актуально в сетях мегаполисов с разветвленной распределитель-

ной сетью, неравномерным графиком нагрузки, большой удельной нагрузкой на источни-

ках питания [6]. Помимо этого реконфигурация распределительных сетей является важной

эксплуатационной задачей, эффективное решение которой помогает значительно снизить

потери при распределении, сбалансировать нагрузки и улучшить надежность электро-

снабжения конечных потребителей, что, в свою очередь, в долгосрочной перспективе

обеспечивает значительные экономические стимулы.

 Экономические аспекты РГ и управления распределительной сетью формируют

отдельный блок исследований. В рыночных условиях принимаемые решения сопровож-

даются финансовыми рисками. Основными целями, которые ставят перед собой исследо-

ватели, являются обеспечение инвестиционной привлекательности в долгосрочной пер-

спективе, повышение экономичности работы сетей, минимизация сроков окупаемости

проектов посредством регулирования цен на энергоносители, снижение тарифов на элек-

троэнергию и другие [7].

В действительности вопрос ценообразования в сетях с РГ стоит достаточно остро и

требует всестороннего изучения для получения наиболее экономически эффективной схе-

мы. Главной целью ценообразования в распределительных сетях является эффективное и

экономичное распределение части или всех существующих и новых издержек на потреби-

телей. В рыночных условиях, в краткосрочной перспективе, система должна работать эф-

фективно, а в долгосрочной перспективе в развитие сети должны эффективно привлекать-

ся инвестиции. Интеграция РГ в сеть делает ее активной. Следовательно, менеджмент ак-

тивных распределительных сетей становится ключом к ценообразованию, что позволит

влиять на поведение потребителей, обеспечивая наиболее экономичную работу распреде-

лительной сети.

 Чистые и возобновляемые источники энергии представляют большой интерес для

исследований. Ввиду новизны технологий «чистой» генерации многие проблемы, связан-