Сборник докладов - Безопасность движения в городах (Иркутск, 21-22 июня 2010 г.)
Подождите немного. Документ загружается.


19
УДК 625.7
Michael Rohloff, DirProf.
BASt
NEUE RICHTLINIEN FÜR LICHTSIGNALANLAGEN 2010

20
Lichtsignalanlagen sind mittlerweile für eine sichere und leistungsfähige Abwicklung des Straßenverkehrs
unentbehrlich. Sie dienen der sicheren Führung des Fußgänger- und Fahrradverkehrs, der Bündelung der
Kraftfahrzeugströme und der Beschleunigung des öffentlichen Verkehrs sowohl an einzelnen Knotenpunkten als
auch auf längeren Streckenabschnitten und in ganzen Straßennetzen.
21
Die Richtlinien für Lichtsignalanlagen (RiLSA) sind das verbindliche Regelwerk zur Gestaltung und zum
Betrieb dieser Anlagen, das nicht nur verkehrstechnischen, sondern auch den verkehrsrechtlichen Anforderungen
genügen muss. Sie sind deshalb eng verzahnt mit den rechtlichen Festlegungen zur Ordnung des Straßenverkehrs
(StVO).
Um den technischen Neuerungen, aber auch den über die Zeit eintretenden Verhaltensänderungen sowie
den Verkehrszuwächsen Rechnung zu tragen, wurden die RiLSA, deren erste Ausgabe aus dem Jahr 1964
stammt, regelmäßig fortgeschrieben. Die letzte Fassung stammte aus dem Jahr 1992 und wurde mit einer
eigenständigen Teilfortschreibung 2003 ergänzt.
In der aktuellen Neufassung 2010 wurden – bei Beibehaltung der bewährten Grundstruktur - aktuelle
Erkenntnisse berücksichtigt, der Richtliniencharakter stärker betont und die unterschiedlichen Verkehrsarten
gleichberechtigt in eigenen Kapiteln behandelt. Außerdem wurden die Richtlinien zur Vermeidung von
Dopplungen gestrafft und praxisgerechter gestaltet.
Neben neuen Entwicklungen bei den Steuerungsverfahren finden auch erstmalig Erfahrungen über die
Sicherheitswirkungen unvollständiger Signalisierungen Berücksichtigung. Ebenfalls neu ist ein Kapitel
„Qualitätsmanagement“, das eine dauerhaft sichere Funktion über die Lebensdauer der Signalanlagen
sicherstellen soll.
Eine separate Beispielsammlung gibt praxisgerechte Hinweise und zeigt Anwendungsmöglichkeiten der
Richtlinie auf; sie wird wegen ihrer geringeren Verbindlichkeit schneller an die technischen Entwicklungen
angepasst werden können als die eigentliche Richtlinie.
22
УДК 625.7
Horst Schulze, Dr.
BASt
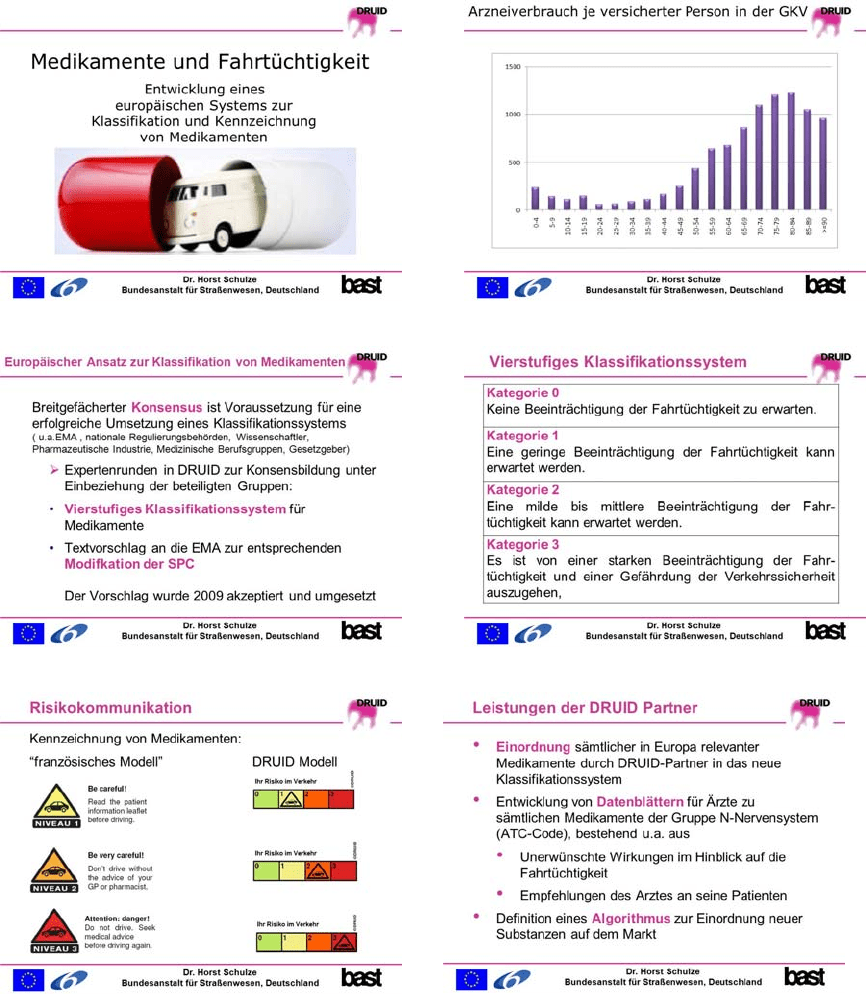
DRIVING UNDER THE INFLUENCE OF DRUGS, ALCOHOL AND MEDICINES (DRUID):
KLASSIFIZIERUNG UND KENNZEICHNUNG VON MEDIKAMENTEN IM HINBLICK AUF
IHRE BEEINTRÄCHTIGUNG DER FAHRTÜCHTIGKEIT

23
Bestimmte Medikamente können, ähnlich wie Drogen oder Alkohol, eine Beeinträchtigung der
Fahrtüchtigkeit und damit der Verkehrssicherheit bewirken. Es ist dabei unerheblich, ob diese Medikamente
bestimmungsgemäß, also wie vom Arzt verordnet, oder missbräuchlich eingenommen werden. Im Rahmen des
europäischen Forschungsprojekts DRUID wird in einem speziellen Unterprojekt ein umfassendes Modell zur
Klassifizierung und Kennzeichnung von Medikamenten im Hinblick auf deren beeinträchtigende Wirkung
entwickelt.
Da im Bereich der pharmazeutischen Versorgung sowohl auf nationaler wie auch auf europäischer Ebene
eine Vielzahl unterschiedliche Verbände, Interessengruppen und Institutionen maßgeblich beteiligt sind, ist es
unbedingt notwendig, alle Akteure in die Überlegungen mit einzubeziehen, um so die Voraussetzung für einen
breiten Konsens zu schaffen.
Vor diesem Hintergrund wurden im Rahmen von DRUID mehrere Experten-Workshops mit Akteuren aus
allen Bereichen organisiert, in welchen wissenschaftliche, rechtliche und organisatorische Aspekte einer
harmonisierten Vorgehensweise für ganz Europa eingehend erörtert und ein entsprechender Plan zur Umsetzung
entwickelt wurden. Ein erstes Ergebnis der intensiven Fachgespräche und Diskussionen ist ein vier-stufigem
Klassifikations- und Kennzeichnungssystems für unterschiedliche Risikograde. Der entsprechende Textentwurf
für eine Änderung der SPC (Summary of Product Characteristics) wurde 2009 von der zuständigen EMA
(Europäische Arzneimittelagentur) akzeptiert und 2009 in deren europäische Bestimmungen aufgenommen.
Im weiteren Verlauf des Projekts wurde das Klassifikationsmodell inhaltlich ausgestaltet und für eine
Umsetzung in die Praxis ausformuliert. Weiterhin wurden Entwürfe für die Kennzeichnung der
Medikamentenpackungen entwickelt, deren Akzeptanz derzeit in einem Pilotversuch getestet wird. Die
Klassifikation der wichtigsten auf dem Markt befindlichen Medikamente durch DRUID-Wissenschaftler ist
derzeit bereits weitgehend abgeschlossen. Für mehrere 100 Medikamente wurden entsprechende „Fact-Sheets“
mit detaillierten Informationen zu Medikamentenprofilen, Wirkungen sowie Hinweisen, welche Informationen
Ärzte ihren Patienten geben sollten, erstellt. Zusätzlich wurde eine Methode zur Fortschreibung entwickelt, auf
welche Weise neu auf den Markt gebrachte Medikamenten in das DRUID- System einzuordnen sind.
Eine praktische Erprobung des neuen Klassifizierungssystems findet momentan in drei europäischen
Ländern (Niederlande, Belgien, Spanien) statt. Hierzu wurden die entsprechenden Modifikationen in bestehende
Computer-Programme für Arztpraxen vorgenommen. Zukünftig werden Ärzte damit unmittelbar bei der
Verordnung eines Medikaments die Information erhalten, inwieweit dieses die Fahrtüchtigkeit beeinträchtigen
kann, und können ihren Patienten bei Bedarf einen entsprechenden Hinweis sowie zusätzliche
Informationsmaterialien geben.

24
УДК 625.7
Raschid Urmeew, Dr.
BASt
DRIVING UNDER THE INFLUENCE OF DRUGS, ALCOHOL AND MEDICINES (DRUID)
DRUID ist ein Forschungsprojekt im Rahmen des 6. EU-Forschungsprogramm.
Die BASt trägt als Projektkoordinator die Gesamtverantwortung für Management und Qualitätssicherung.
Beteiligt sind 37 Forschungsinstitutionen aus 18 europäischen Ländern (17 EU-Mitgliedsländer und
Norwegen). Das EU-Förderbudget beträgt 18,9 Mio. €.
Ziel des Projekts ist, interdisziplinär und ganzheitlich alle relevanten Aspekte des Fahrens unter dem
Einfluss psychoaktiver Substanzen zu untersuchen und die Verkehrssicherheitspolitik der EU zu unterstützen.
Arbeitsschwerpunkte:
1. Methodologie und Experimente: Experimentelle Untersuchung der Beeinträchtigung der Fahrtüchtigkeit
durch psychoaktive Substanzen. Empfehlung von Grenzwerten für psychoaktive Substanzen in Analogie zu
Alkohol-Promille-Werten.
25
2. Epidemiologie: Bereitstellung einer Datenbank zur Häufigkeit von Fahrten unter dem Einfluss
psychoaktiver Substanzen in Europa.
3. Polizeiliche Überwachung: Evaluation von Drogenschnelltests.
4. Klassifikation: Entwicklung eines Klassifikations- und Kennzeichnungssystems für Medikamente
hinsichtlich ihres Einflusses auf die Fahrtüchtigkeit.
5. Rehabilitation: Bewertung und Empfehlung von Rehabilitationsmaßnahmen.
6. Führerscheinentzug: Bewertung und Empfehlung von Rechtspraktiken.
7. Dissemination: Entwicklung von Informationsmaterialien für unterschiedliche Zielgruppen.
Erwartete Ergebnisse:
• Überblick über die aktuelle Situation in Europa
• Risikoabschätzung für verschiedene Substanzen
• Empfehlungen für analytische und Risiko-Grenzwerte
• Vorschläge für effektive Strategien zum Drogennachweis
• Etablierung und Fortschreibung eines Europäischen Klassifikationssystems für Medikamente
• Entwicklung einheitlicher Kriterien und Standards für Rehabilitationsmaßnahmen
• Empfehlung von Maßnahmen, die das Unfallrisiko reduzieren und die Mobilität so weit wie möglich
erhalten
• Entwicklung und Verbreitung von Informationsmaterial für Patienten, die allgemeine Öffentlichkeit,
junge Fahrer, Drogenkonsumenten und medizinische Berufsgruppen

26
УДК 656.13.021:004.94
Сильянов В.В., д.т.н., профессор
Елисеева С.А., с.н.с., Уткин А.В., к.т.н., с.н.с.
Проблемная лаборатория организации и безопасности дорожного движения-ПЛОБД, МАДИ
МОДЕЛИРОВАНИЕ ЦЕПНЫХ КРИТИЧЕСКИХ СИТУАЦИЙ
В ПЛОТНОМ ТРАНСПОРТНОМ ПОТОКЕ

27

28
Проведено исследование влияния макроскопических неоднородностей на распределение
критических ситуаций (КС) в транспортном потоке с помощью численного эксперимента. Разработан
графический метод анализа мест концентрации КС в транспортном потоке. Показано, что КС имеют
место, прежде всего, на границе скачков уплотнения в потоке. Вычислительный эксперимент позволил
выявить наличие цепных КС в моделируемой системе
. Определено, что скорость распространения
цепных КС может в три раза превышать скорость распространения ударной волны в транспортном
потоке.
Ключевые слова: математическая модель транспортного потока, ударные волны, транспортные
пробки, время до столкновения, места концентрации критических ситуаций, цепные критические
ситуации, показатели безопасности дорожного движения.
Возросший уровень автомобилизации, переполнение дорожной сети, усложнение условий
движения в первую очередь в городах ставят задачу исследования влияния заторов («пробок») и ударных
волн в транспортном потоке на безопасность движения (БД). Дорожно-транспортное происшествие
(ДТП) является относительно редким событием, а частота ДТП нестабильна по своей природе. Поэтому в
качестве меры уровня БД используются транспортные конфликты (ТК). Предполагается, что причины
,
лежащие в основе ТК и ДТП, одни и те же. Общепринятой мерой измерения ТК является время до
столкновения (
TTC ).
Целью работы являлось исследование количественных показателей уровня БД в транспортном
потоке с макроскопическими неоднородностями. Только эмпирическое решение этого вопроса не даёт
соответствующего затратам эффекта, поэтому математическое моделирование распределения ТК в
транспортных потоках является важной практической задачей.
Использована модель транспортного потока, которая является достаточно простой для реализации,
но в то же
время хорошо описывает качественные характеристики транспортного потока [1,2]. Модель
характеризуется в основном тремя свободными параметрами, два из которых описывают способность
автомобиля к замедлению и ускорению, а третий (стохастический элемент), задаёт несовершенство
поведения водителя (отклонение от идеальной траектории). Модель, использует непрерывные
пространственные координаты и дискретна по отношению ко времени. Она применима для исследования
уровня БД в транспортных потоках смешанного состава [3].
Подход основан на рассмотрении тормозных путей, то есть на наблюдении, что сумма тормозного
пути и пути, пройденного ведомым автомобилем за время реакции водителя, должна быть меньше, чем
тормозной путь автомобиля впереди плюс расстояние между автомобилями:
