Савельев А.В. Проектирование электромеханических аппаратов автоматики с применением ЭВМ
Подождите немного. Документ загружается.

P
P
мх.н
P
мх.к
к
н
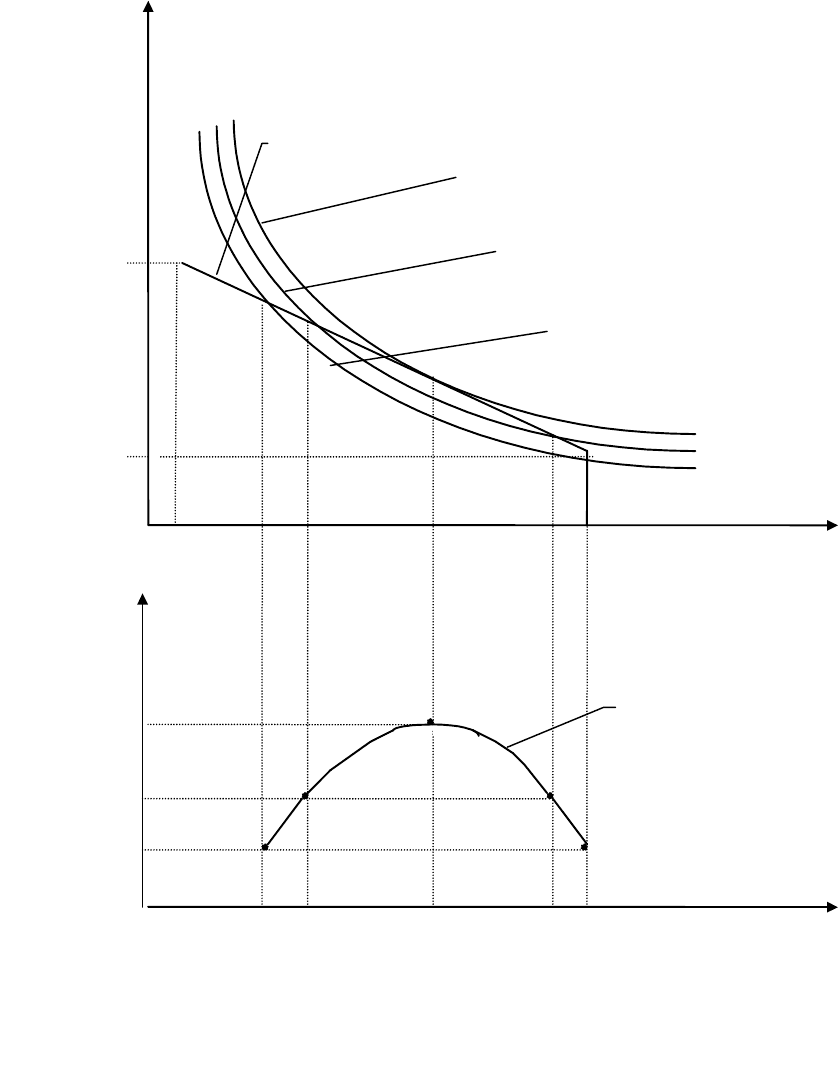
Рис. 4.1. Получение зависимости статической МДС F oт зазора
P
мх
(
)
P
э
(
) при F
3
=F
сраб
P
э
(
) при F
2
P
э
(
) при F
1
F
F
1
F
2
F
3
=F
сраб
сраб
0
F(
)
40
5. PАСЧЕТ ОБМОТКИ ПОСТОЯННОГО ТОКА
Расчет обмотки постоянного тока предусматривает
определение диаметра и числа витков обмоточного провода,
обеспечивающих требуемую рабочую МДС F
раб
и приемлемый
перегрев
.
Рабочая МДС электромагнита с обмоткой напряжения
N
R
U
FKF
срабзраб
. (5.1)
Здесь K
з
- коэффициент запаса (K
з
= 1,3-2,0); F
сраб
- МДС
срабатывания; N - число витков; U - напряжение; R
- сопротивление
обмотки при температуре
определяемое выражением
R
D N
d
с
р
2
4
, (5.2)
где
- удельное электрическое сопротивление провода при
температуре
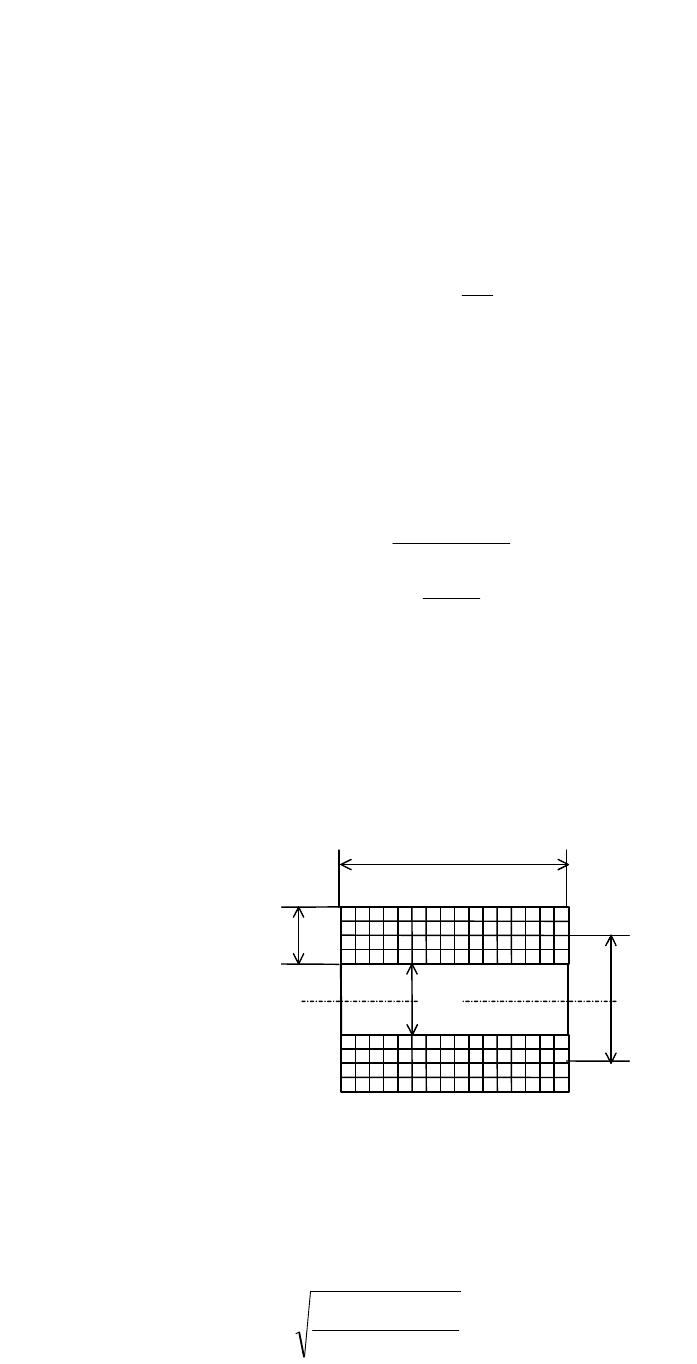
; D
ср
- средний диаметр обмотки (рис. 5.1); d -
диаметр провода без изоляции.
Рис. 5.1. Эскиз обмотки
l
o
h
о
D
в
D
ср
Из (5.1) и (5.2) следует, что диаметр провода без изоляции
d
F
D
U
аб
с
р
р
4
. (5.3)
41

Получаемое из (5.3) значение диаметра провода округляется до
стандартного, указанного в приложении 3 (табл. П3.4).
Превышение температуры обмотки
P
K S
Т
охл
,
(5.4)
где P- мощность, выделяемая в обмотке; K
Т
- коэффициент
теплоотдачи (рис.5.2); S
охл
- площадь охлаждаемой поверхности.
0
2
4
6
8
10
12
14
30 50 70 90 110
,
o
C
K
Т
,Bт
/м
2 o
C
а
б
Рис. 5.2. Зависимость коэффициента теплоотдачи K
Т
от
превышения температуры [3]:
а - бескаркасная катушка;
б - каркасная катушка.
Полная поверхность охлаждения состоит из боковой и
торцевой поверхностей, т.е.
S
охл
= S
бок
+ S
торц
, (5.5)
причем теплоотдача с внутренней боковой поверхности и с торцев
значительно меньше, чем с наружной поверхности.
Мощность, выделяемая в обмотке напряжения
42

P
U
R
2
. (5.6)
Получаемые при расчете обмоточных данных МДС F
рас
и
превышение температуры
рас
должны соответствовать
соотношениям:
р рас аб
F F
;
рас допуст
.
Pасчетный модуль “obmot.bas”, предназначенный для
определения основных обмоточных данных катушки постоянного
тока, приведен в приложении 2 (П2.6). Подпрограмма типа
SUBROUTINE, входящая в состав расчетного модуля, предназначена
для контроля за приемлемостью вводимых значений.
43
6. PАСЧЕТЫ ДИНАМИЧЕСКИХ ХАРАКТЕРИСТИК
ЭЛЕКТРОМАГНИТА ПОСТОЯННОГО ТОКА
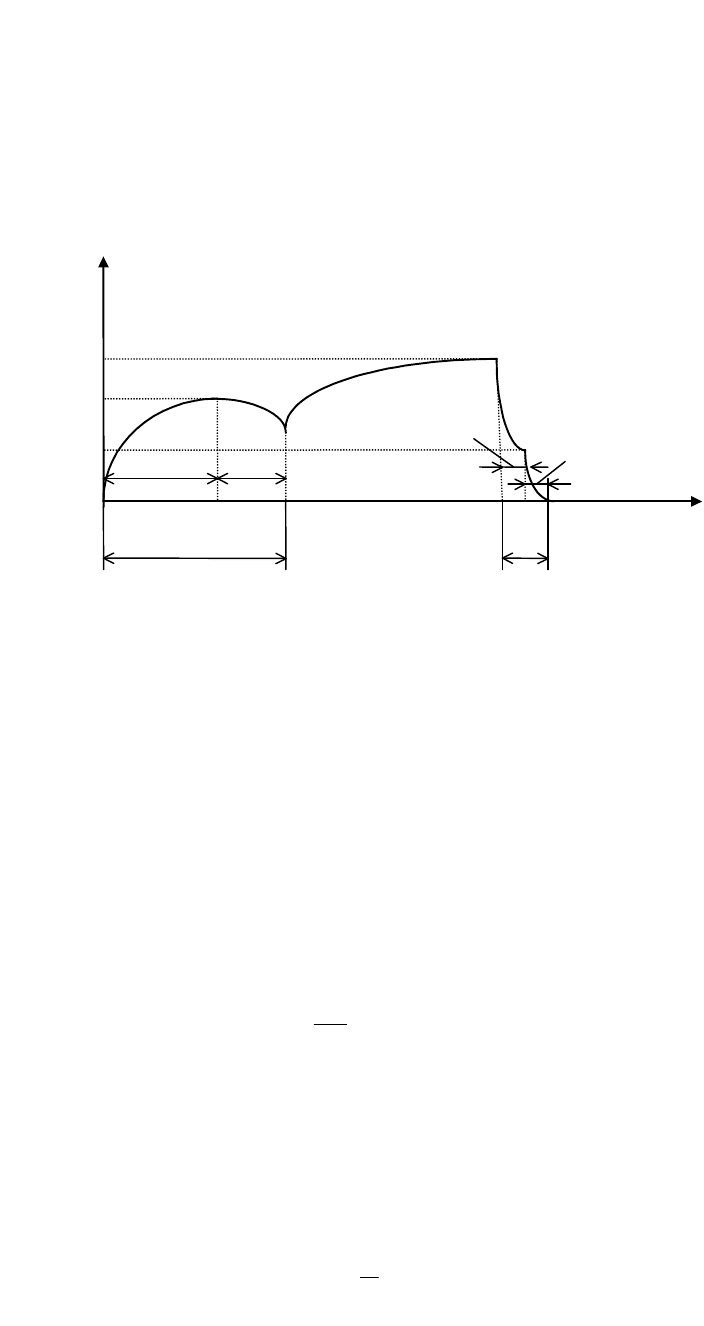
Динамические характеристики электромагнитов постоянного
тока характеризуются временем срабатывания t
ср
и временем
возврата (отпускания) t
в
(рис. 6.1).
i
у
i
тр
i
в
i
t
ср
t
t
в
t
тр.в
t
дв.в
t
тр.ср
t
дв.ср
0
Рис. 6.1. Динамика работы электромагнита
Время срабатывания электромагнита складывается из времени
трогания при срабатывании t
тр.ср
и времени движения при
срабатывании t
дв.ср
:
t
ср
= t
тр.ср
+ t
дв.ср
. (6.1)
Время трогания при срабатывании находят исходя из
уравнения баланса напряжений
u iR
d
dt
. (6.2)
Здесь i - ток; R - активное сопротивление цепи обмотки при
срабатывании;
- потокосцепление; t - время.
Для линейной магнитной системы решение уравнения (6.2)
имеет вид
e
н
t
у
i
i
1
, (6.3)
44

где
н
= L
н
/R - электромагнитная постоянная времени при начальном
зазоре (L
н
- индуктивность магнитной системы при начальном зазоре
н
, R - активное сопротивление цепи обмотки при срабатывании); i
у
= U/R - установившееся значение тока (U - напряжение)).
Решив (6.3) относительно t
= t
тр.ср
получим формулу времени
трогания при срабатывании
1
lnln
р
.р
р
К
К
ii
i
R
L
t
з
з
н
у
у
н
т
т
с
. (6.4)
Здесь i
тр
- ток трогания; К
з
- коэффициент запаса.
Время движения электромагнита постоянного тока
определяют исходя из двух уравнений: уравнения баланса
напряжений (6.2) и уравнения баланса сил
э мх
P
m
d
x
dt
P
2
2
. (6.5)
Здесь P
э
- электромагнитная сила; P
мх
- механическая сила; m -
приведенная масса подвижных частей электромагнита; x -
перемещение якоря ; t - время. В общем случае P
мх
и P
эм
зависят как
от положения, так и от скорости перемещения якоря.
Известны две группы методов решения уравнений (6.2) и (6.5)
при расчете динамических характеристик: во-первых, методы,
основанные на делении перемещения якоря на ряд последовательных
интервалов и, во-вторых, методы, дающие общие математические
выражения динамических характеристик на основе упрощений
реального процесса [10].
Из первой группы методов отметим метод, предложенный
Н.Е.Лысовым , который позволяет рассчитать время движения при
любой форме зависимостей потокосцепления от тока (без учета
вихревых токов в магнитопроводе).
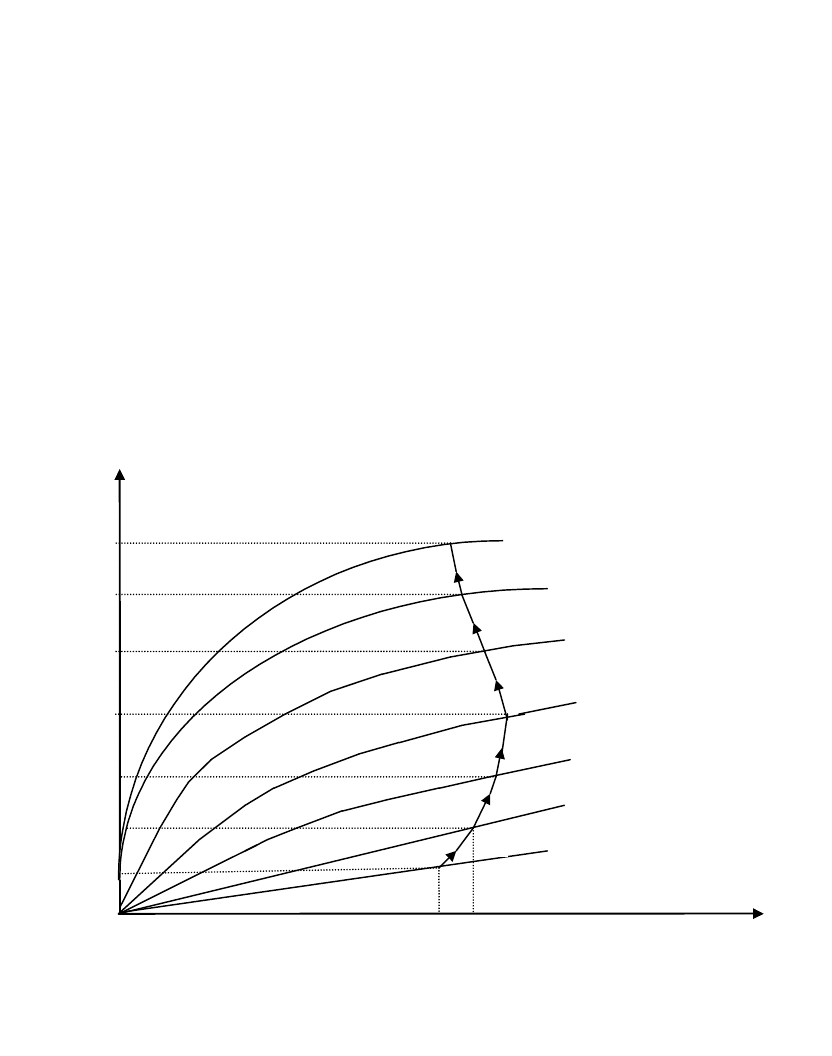
Для практического использования метода последовательных
интервалов при нахождении времени движения якоря
электромагнита по известным зависимостям
i
(рис. 6.2) и
механической характеристике уравнение (6.5) после преобразований
записывают в следующем виде
э
k
k
к н
мх
k
k
P
d
mv mv
P
d
1
2 2
1
2 2
.k .k
.
(6.6)
45
Здесь v
к.k
- скорость в конце интервала при текущем зазоре
k
(k =
1,2,3,..), v
н.k
- скорость в начале интервала при зазоре
k-1
.
Порядок расчета методом последовательных интервалов
предусматривает следующие этапы:
1) Из кривой
i
(рис.6.2) при
=
н
по току i
тр
находится
н
.
2) На кривой
i
(рис.6.2) при
=
k
выбирается
k
>
k-1
и
соответствующее значение i
k
.
3) Для нахождения приближенного значения
э
k
k
P
d
1
,
характеризующего работу электромагнитной силы на
интервале, рассчитывается площадь криволинейного
треугольника (для первого интервала при k = 1 - площадь
ОАБ).
4) Из механической характеристики находится значение
мх
k
k
P
d
1
, характеризующего работу механической силы
на интервале.
Рис.6.2. К расчету времени движения электромагнита
i
i
тр
i
1
А
к
3
2
1
н
5
4
Б
0
к
5
4
3
2
1
н
46

5) Определяется скорость в конце интервала
к э мх
н
v
m
P
d
m
P
d
v
k
k
k
k
.k
.k
2 2
1 1
2
. (6.7)
6) Рассчитывается средняя для интервала скорость
c
к
v
v
v
н k
.k
.k
.
2
. (6.8)
7) Определяется время движения для интервала
дв
t
k k
c
v
.k
.k
1
. (6.9)
8) На основе (6.2) проверяется правильность выбора
k
t
R
ii
u
kдв
kk
kk
.
1
1
2
. (6.10)
Если (6.10) не выполняется, то проводится коррекция выбора
k
, на
этапе 2.
9) Определяется время движения при срабатывании
дв с
k
n
дв
t t
. р .k
1
. (6.11)
Время движения при срабатывании быстродействующего
электромагнита постоянного тока при допущении о постоянстве
противодействующей силы, а также без учета потоков рассеяния,
насыщения стали, вихревых токов определяется по формуле [10]
дв с
н
мх с
н
н
мх с
н
t
m
U
P
L
R
P
L
. р
. .
3
2
3
, (6.12)
47
где P
мх.
с
- усредненная механическая сила.
48
Время возврата (отпускания) электромагнита складывается из
времени трогания при возврате t
тр.в
и времени движения при
возврате t
дв.в
:
t
в
= t
тр.в
+ t
дв.в
. (6.13)
Для линейной магнитной системы время трогания при возврате
электромагнита постоянного тока определяется выражением
К
К
i
i
i
i
i
i
t
в
з
к
в
у
к
в
у
к
в
lnlnln
тр
тр
тр.
, (6.14)
где i
в
= I
в
- ток возврата (отпускания);
к
- электромагнитная
постоянная времени при конечном зазоре; К
в
- коэффициент
возврата.
Время движения при возврате (отпускании) электромагнита
постоянного тока рассчитывается методом последовательных
интервалов по аналогии с расчетом времени движения при
срабатывании.
49
