Сарычева Л.И. Физика фундаментальных взаимодействий
Подождите немного. Документ загружается.


σ
tot
= σ
el
+ σ
inel
+ σ
qel
a + b = a + b
a + b = a + b + c
1
+ c
2
+ . . . + c
n
a + b = c
i
+ X i = 1 ÷n X

a + b = a + b + X X
X
e
±
p
µ
±
p γp νp ¯νp e
+
e
−
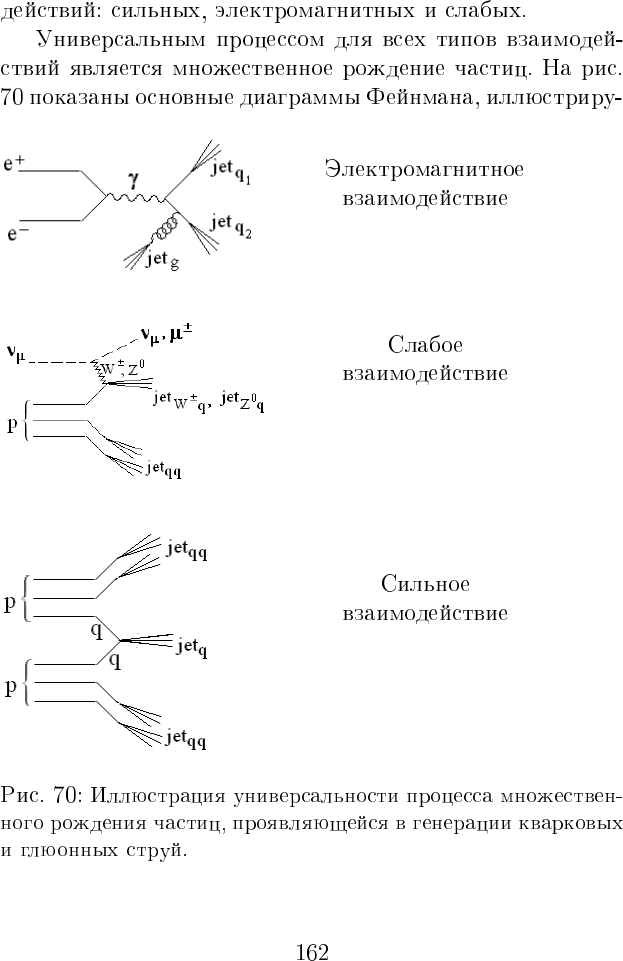
e
+
+ e
−
→ jet
q
1
+ jet
q
2
+ jet
g
ν
µ
+ p = ν
µ
+ jet
W
±
q
+ jet
qq
ν
µ
+ p = ν
µ
+ jet
Z
0
q
+ jet
qq
p + p = jet
q
+ jet
q
1
q
2
+ jet
q
3
q
4

p
⊥
exp
−bp
⊥
p
−n
⊥
p
⊥
> 1 c
”
“
”
“
p
⊥

p
⊥
< 1 c
hp
⊥
i ∼ 0.3 c
p
⊥
> 1 c
µ
±
e
±
γ

n
n
ch
n
i
i
π
−
, π
+
, π
0
, K
±,0
, p, ¯p
c
a + b = c + X
hn
c
i = σ
X
n
nσ
n
(c),
σ
n
(c) n
c σ

a + b =
c + X
hn(s)i =
1
σ
in
Z
f(x, p
⊥
, s)d
3
p/E.
n
±
σ
n
±
(s) =
X
n≥n
±
σ
n
(s),

n
σ
n
(s)
s
σ
n
±
(s)
pp
π
+
p ¯pp π
−
p
K
−
p K
+
p
pp π
+
p K
+
p ¯pp π
−
p K
−
p
σ
0
σ
2
σ
4
(σ
0
)
σ
0
= ap
−n
a = 57
n = 1.51 ± 0.16 π
−
p pp a = 6 1
n = 1.46 ± 0.15
D hni/D
x z = n/hni
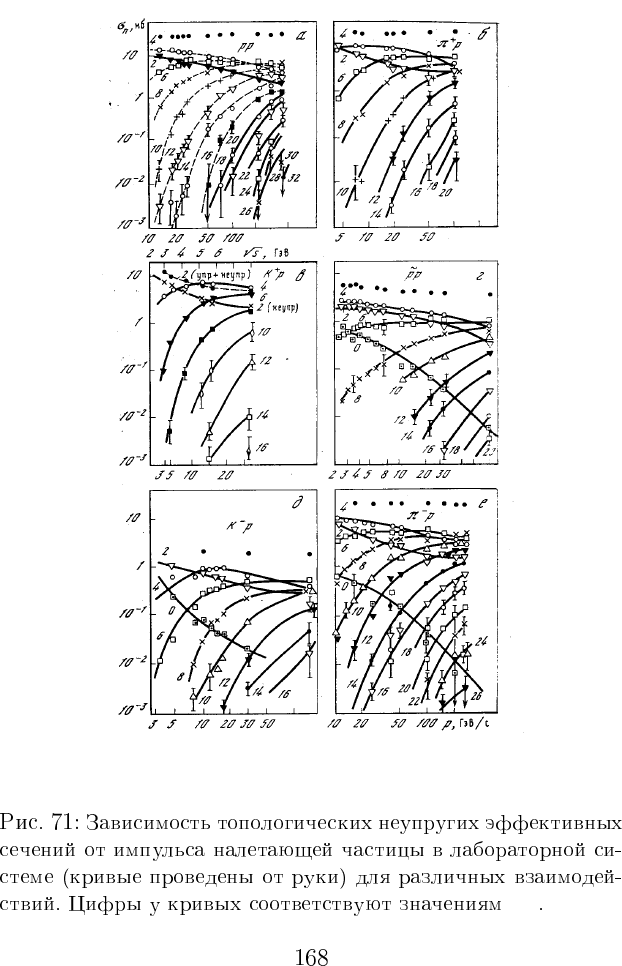
n
±

lim f(x, p
⊥
, s)
s→∞
= f (x, p
⊥
)
s
a + b = c + X
c
hn
c
ab
i = 2
1
R
x=0
∞
R
p
⊥
f
c
ab
(x, p
2
⊥
)
d
2
p
⊥
dx
q
x
2
+
4m
2
⊥
s
=
= hf
c
ab
(x = 0)iln
s
m
2
⊥
+ const.
s
hf(x)i x p
⊥
KNO
n
z =
n/hni
hni
√
s
hniP
n
(s) = hni
σ
n
(s)
σ
tot
(s)
= ψ
n
hni
!
,
σ
n
(s)
KNO
KNO
