Салимов Р.Б. Математика (для студентов бакалавриата)

Подождите немного. Документ загружается.

221

гласно формуле (20), выражаются через соответствующие определённые ин-

тегралы, поэтому Отсюда

(21)

Эта формула справедлива и в том случае, когда

совпадает с а – с В качестве примера

найдём площадь конечной фигуры, заключённой

между линиями и

,yx=

пересекающимися в

точке

( )

0,0O и точке с координатами

1, 1,xy= =

по-

скольку координаты каждой из указанных точек удо-

влетворяют уравнениям обеих кривых (рис. 115).

Эта фигура лежит между прямыми и Её площадь определяет-

ся по формуле (21), в которой Итак,

( )

2 23

( ) /2 /3 1/6.S x x dx x x=−=− =

∫

Пусть теперь на плоскости кривая (см. рис. 116) задана парамет-

рическими уравнениями

(22)

При этом

(23)

Здесь, как и ранее, Функция

()t

и производная

()t

′

непрерывны в ин-

тервале

[ , ].

αβ

Из первого уравнения (22) выразим через и найдём функ-

цию обратную к Полученное выражение подставим во второе

уравнение (22) и найдем Воспользуемся формулой (20), где вме-

сто возьмём

[ ( )]:tx

(24)

Сделаем замену

()xt

согласно первому уравнению (22), при этом

и подинтегральная функция По теореме о замене

переменной в определенном интеграле пределы

,x ax b= =

интеграла формулы

( ) ( )

2112

AABB

S f x dx f x dx= −

∫∫

( ) ( )

2112

AABB

S f x f x dx= −





∫

yx=

0xa= =

1.xb= =

( )

,fx x=

( )

.fx x=

Oxy

( )

,xt

( )

,yt

αβ

≤≤

( )

ϕα

( )

ϕβ

.ab<

( )

,t tx=

( )

.xt

( )

.y tx





( )

aABb

S t x dx





∫

( )

dx t dt

′

( ) ( )

.tx t

ψψ





Рис. 115

5354.ru

222

(24) мы должны заменить соответствующими пределами

,tt

αβ

= =

согласно

(23). Следовательно, (24) примет вид

(25)

Эта формула позволяет найти площадь криволиней-

ной трапеции, когда кривая задана параметриче-

ски уравнениями (22) (рис. 116). В ней может быть

как меньше, так и больше важно лишь, что значе-

нию отвечает точка с абсциссой меньшей

абсциссы

точки

Пример. Вычислим площадь

эллипса, заданного параметрическими урав-

нениями

cos , sin , 0 2 .xa tyb t t

= = ≤≤

(26)

Точка определяемая по (26), при изме-

нении от до пробегает весь эллипс, начи-

ная от точки

(см. рис. 117), против хода часо-

вой стрелки. При точка эллипса совпадает

с точкой

Найдём – площадь четверти эллипса, лежащего в первой четверти

плоскости Эта фигура сверху ограничена кривой Точке отвечает

следовательно,

/2.

απ

Точке отвечает следовательно,

= 0

Здесь

() cos, () sin,ta t tb t

ϕψ

= =

и по формуле (25) имеем

11 0 11 11

( /2)[ (1/2)sin2 ] /4; .ab t t ab S ab

ππ

=−==

( ) ( )

aABb

S t t dt

ψϕ

′

∫

( )

,,xy

.Oxy

.AB

2,t

0,t =

( )

1 1 11 11

2 00

1 cos2

sin sin sin

b t a t dt a b tdt a b dt

ππ

−

= ⋅− = = =

∫ ∫∫

Рис. 116

Рис. 117

223

§ 7. Площадь криволинейного сектора

Пусть в плоскости задана точка Пусть – длина отрезка

и – угол между осью и вектором отсчитываемый от оси и счи-

тающийся положительным, когда отсчёт ведётся против хода часовой стрелки

(рис. 118). Из рис. 118 видно, что

cos , sin .xy

ρθ ρθ

= =

(27)

Числа и – полярные координаты точки у

которой – декартовы координаты. Формула (27),

как отмечалось в § 2 главы 1, связывает декартовы

координаты с её полярными координатами.

Пусть полярная координата (полярный радиус) точки есть функция

()f

ρθ

от полярного угла

Тогда с изменением расстояние

точки до начала координат изменится и на плоскости опишет некото-

рую линию. Соотношение называется уравнением этой линии в по-

лярных координатах.

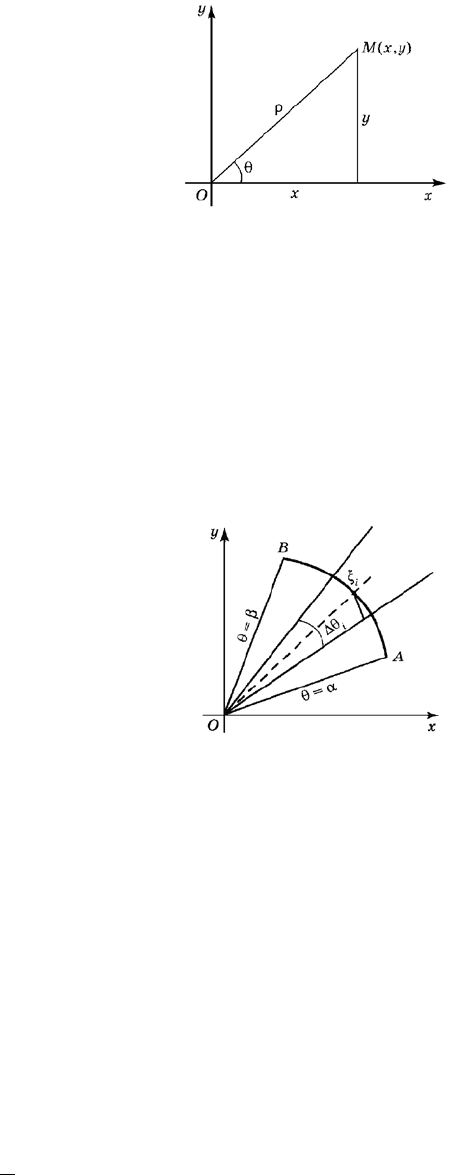
Пусть кривая на плоскости задана в по-

лярных координатах уравнением

( ),f

ρθ

где

(рис. 119). Функцию считаем непрерывной в ука-

занном интервале. Кривая

находится между пря-

мыми и уравнения которых в полярных коор-

динатах будут соответственно и

θβ

(по анало-

гии с уравнениями и прямых, параллельных

оси

).Oy

Получили криволинейный сектор ограниченный отрезками

и линией

.AB

Требуется найти его площадь .

Разобьём сектор на частичных секторов, проведя через точку лучи

причём где Рассмот-

рим сектор, ограниченный лучами и

θθ

−

с углом Заме-

ним его круговым сектором, радиус которого равен и

θ θθ

−

≤≤

а площадь равна Это построение выполним для

всех частичных секторов и получим фигуру, составленную из круговых

секторов. Вычислим ее площадь Устремим число секто-

Oxy

( )

,.Mxy

,OM



,xy

( )

OM f

ρθ

= =

( )

ρθ

Oxy

αθ β

≤≤

( )

,OB

θα

xa=

xb=

,OAB

,OA

OAB

12 1

, ,... , ,

θθθθ θθ

−

= = =

012 1

... ,

θθθ θ θ

−

<< << <

θ αθ β

= =

θθ

θθθ

−

∆= −

( )

i ii

θ ξθ

−

≤≤

( )

(1/ 2) .

ξθ

∆





( )

n ii

ξθ

= ∆





∑

Рис. 119

Рис. 118

5354.ru

224

ров к бесконечности так, чтобы наибольший из углов частичных секторов

стремился к нулю, при этом все секторы будут стягиваться в отрезки

и ступенчатая фигура по форме будет приближаться к криволинейному сек-

тору. Таким образом, площадь этого криволинейного сектора будет равна

( )

max 0,

lim .

OAB i i

ξθ

∆→

= ∆





∑

Под знаком предела стоит интегральная сумма

для непрерывной функции

( )/2f

в интервале Поэтому этот предел

равен определённому интегралу от названой функции, взятой в интервале

Итак,

(1/ 2) ( ) .

OAB

S fd

θθ

∫

(28)

Пример. Рассмотрим кривую, определённую

уравнением – заданное положительное чис-

ло. Легко выяснить форму этой кривой. Пусть уве-

личивается, начиная от значения

Тогда расстоя-

ние точки до начала координат увели-

чивается и отдаляется от (с ростом ) тем

дальше, чем больше

и кривая уходит в бесконечность. Эта кривая называ-

ется спиралью Архимеда (см. рис. 120).

Найдём площадь заштрихованного криволинейного сектора, ограничен-

ного указанной кривой и лучами и По формуле (28) найдем

[ ]

3 2 23

2 33

11 7

( ( /2) ) .

2 2 3 6 48

OAB

S ad a

θπ

θθ π π

= = =−=

∫

§ 8. Вычисление длины дуги кривой

Пусть на плоскости кривая задана

уравнением причём –

абсциссы точек соответственно. Будем

считать, что функция имеет непрерывную

производную всюду в интервале

[ ]

,.ab

Кривую

(см. рис. 121) разобьём на частей точка-

ми причём каждая по-

max

∆

[ ]

αβ

[ ]

αβ

ρθ

OM a

ρθ

= =

( )

0, 0

θπ

Oxy

( )

,y fx=

,axb≤≤

,ab

,AB

( )

12 1 1

, ,..., , ,..., ,

ii n

MM M M M

−−

Рис. 120

Рис. 121

225

следующая точка лежит правее предыдущей. Точки будем обозначать

соответственно Каждые две соседние точки деления соединим хордой

и получим ломаную, состоящую из хорд, вписанных в кривую Длина ло-

маной, которую обозначим

равна сумме длин ее звеньев, т. е.

n in

ls s s=∆ + +∆ + +∆

где

s∆

– длина звена Запишем эту длину с по-

мощью символа суммирования:

= ∆

∑

Пусть число делений кривой

стремится к бесконечности так, что длина наибольшего звена

max

s∆

стремит-

ся к нулю. Тогда ломаная, вписанная в кривую по форме будет прибли-

жаться к этой кривой, и за длину дуги кривой естественно принять

, max 0

lim .

→∞ ∆ →

Здесь при

max 0

s∆→

имеем где – наиболь-

шая из проекций звеньев ломаной на ось Таким образом, получим

, max 0

max 0

lim .

→∞ ∆ →

∆→

= ∆

∑

(29)

Пусть – абсциссы точек соответственно

Обозначим и тем самым разобьём интервал эти-

ми точками на частей, каждая длиной

(30)

Точки имеют соответственно ординаты и Ясно, что ве-

личина

(31)

есть катет прямоугольного треугольника, показанного на рис. 119. Другой ка-

тет равен Из указанного треугольника находим гипотенузу, равную

s∆

–

длине -го звена ломаной:

( ) ( )

iii

sxy∆ = ∆ +∆

(32)

По формуле Лагранжа запишем разность

где Левая часть формулы есть согласно (31), а разность в пра-

вой части равна согласно (30). По-этому Подставим по-

следнюю формулу в (32):

,AB

.AB

−

,AB

max 0,

x∆→

max

x∆

.Ox

11 1

,..., , ,...,

ii n

x xx x

−−

,... , ,

−

,... , .

−

,xa=

xb=

[ ]

,ab

i ii

xxx

−

∆= −

−

( )

−

( )

( ) ( )

1iii

fx fx y

−

−=∆

x∆

( ) ( )

1ii

fx fx

−

−=

( )( )

iii

f xx

−

′

= −

i ii

−

≤≤

y∆

x∆

( )

i ii

yf x

′

∆= ∆

5354.ru

226

( )

ii i

sx f

′

∆=∆ +





(33)

Использовав (33), запишем (29) в виде

( )

, max 0

lim 1 .

l fx

→∞ ∆ →

′

= +∆





∑

(34)

Здесь в правой части под знаком предела стоит интегральная сумма для

функции

1 [ ( )]fx

′

, непрерывной в интервале записанная для интер-

вала Поэтому ее предел равен определённому интегралу от этой функ-

ции, взятому по интервалу

[ ]

,.ab

Следовательно

(35)

Эта формула позволяет вычислить длину дуги кривой заданной уравне-

нием – абсциссы точек

В формуле (35), как ясно

из предыдущего, берётся положительное значение корня и, кроме того, в ней

считают, что

Пример. Найдем длину

дуги четверти окруж-

ности с центром в точке и радиусом распо-

ложенной в первой четверти плоскости

Oxy

(рис. 122). Уравнение такой окружности

Отсюда (берем знак «+», так как рас-

сматриваем первую четверть). Здесь и

Найдём и подставим в формулу (35). Получим

1 11

0 00

1 arcsin1 .

11 2

x dx

l dx dx



=+= ===



−−

−



∫ ∫∫

§ 9. Вычисление объёма тела по известным площадям

параллельных сечений. Объем тела вращения

Пусть в системе координат задано тело, расположенное между плос-

костями, перпендикулярными к оси уравнения которых (см.

рис. 124). Указанные плоскости с телом имеют общие точки. Пусть есть

площадь сечения тела плоскостью, перпендикулярной к оси и проходящей

[ ]

,,ab

[ ]

,.ab

( )

l f x dx

′

= +





∫

,AB

( )

,y fx=

,axb≤≤

,ab

,.AB

.ab<

( )

0, 0

1.xy+=

1yx=+−

0,a =

1b =

( )

1.fx x= −

( )

′

Oxyz

,Ox

,xa=

xb=

( )

Рис. 122

227

через точку интервала Будем считать, что эта площадь известна для

любой точки из Примем, что функция непрерывна в

Нужно найти объём по известной функции в интервале

Интервал разобьём на частей точка-

ми Каждая последующая точка ле-

жит правее предыдущей. Обозначим и

Через точки деления проведём

плоскости, перпендикулярные к оси и тем

самым разобьём данное тело на частей. Рас-

смотрим часть, расположенную между плоско-

стями, проведёнными через точки В ин-

тервале возьмём произвольную точку Проведём через

нее плоскость, перпендикулярную к оси и получим сечение, площадь ко-

торого равна Через границу этого сечения проведём цилиндрическую

поверхность с образующими, параллельными оси расположенными меж-

ду плоскостями, проведёнными через точки Получим цилиндр, высота

которого равна Его основания лежат на плоскостях, проходящих

через точки площади которых равны Объём этого цилиндра ра-

вен произведению площади основания на высоту, т. е.

.)(

iii

xSV ∆=

Этим ци-

линдром заменим часть тела, расположенную между плоскостями, проведён-

ными через точки Такое же построение выполним для всех частей, на

которые разбили тело. Получим ступенчатое тело, состоящее из цилиндров,

его объём равен сумме объёмов цилиндров: Число устре-

мим к бесконечности так, что длина наибольшего интервала То-

гда ступенчатое тело будет приближаться к заданному, поэтому естественно

за его объём принять

, max 0

lim .

→∞ ∆ →

Подставив выражение для , получим

( )

, max 0

lim .

V Sx

→∞ ∆ →

= ∆

∑

В правой части под знаком предела стоит интеграль-

ная сумма для непрерывной функции и интервала в котором эта

функция задана. Следовательно, предел указанной интегральной суммы равен

определённому интегралу от функции взятому по интервалу :

[ ]

,.ab

[ ]

,.ab

( )

[ ]

,.ab

( )

[ ]

,.ab

[ ]

,ab

12 1

, ,..., .

xx x

−

xa=

xb=

12 1

, ,...,

xx x

−

,Ox

−

[ ]

−

i ii

−

,Ox

( )

,Ox

−

i ii

xxx

−

∆= −

−

( )

−

( )

n ii

VSx

= ∆

∑

max 0.

x∆→

( )

[ ]

,,ab

( )

,Sx

[ ]

,ab

Рис.

124

5354.ru

228

(40)

Объём тела вращения

Пусть в плоскости кривая задана уравнением

– абсциссы точек

соответственно. Будем считать, что непре-

рывна в интервале и всюду При вра-

щении этой кривой вокруг оси абсцисс получим

поверхность, ограничивающую тело вращения (см.

рис. 125). Требуется найти его объём.

Через точку интервала проведём плос-

кость, перпендикулярную к оси Эта плоскость

пересекает тело по кругу (он показан на рис. 125),

радиус которого равен – ординате точки кривой с абсциссой Яс-

но, что площадь этого круга равна Таким образом, для каждо-

го из интервала известна площадь сечения поэтому для нахож-

дения искомого объёма можем воспользоваться формулой (40):

Пример. Вычислим объём тела вращения, по-

лученного вращением вокруг оси кривой на

плоскости с уравнением

0 x

≤≤

(см.

рис. 126). Итак, При вы-

числении нужно учесть, что

sin x

(1 cos2 ) / 2.x= −

Имеем

( )

0 0 00

sin ( /2) (1 cos2 ) ( / 2) cos2

( / 2) (1/ 2) cos2 2 /2 ( /4)(sin2 sin0)

/2.

V xdx x dx dx xdx

xd x

π π ππ

ππ π

ππ π π π



= =−= − =







= − =− −=





∫ ∫ ∫∫

∫

( )

V S x dx=

∫

Oxy

( )

,y fx=

,axb≤≤

,ab

( )

[ ]

,ab

( )

0.fx>

[ ]

,ab

.Ox

( )

( ) ( )

.Sx fx





[ ]

,ab

( )

,Sx

( )

V f x dx





∫

Oxy

sin ,yx=

0,a =

= ,

( )

sin .fx x=

Рис. 125

Рис. 126

229

§ 10. Приближенное вычисление определенного интеграла

методом трапеций

Если известна первообразная для функции то интеграл

()

f x dx

∫

вычисляется по формуле Ньютона – Лейбница:

() () ().

f x dx F b F a= −

∫

Но не всегда можно представить через элементарные функции, в этих

случаях определённый интеграл вычисляют приближённо. Рассмотрим лишь

один из таких приближённых методов – метод трапеций.

Итак, нужно приближённо вычислить интеграл

() ,

f x dx

∫

где

– заданные числа и а

– заданная в интервале непрерывная

функция. Для простоты предположим, что кривая

с уравнением лежит выше

оси – абсциссы точек

,AB

(рис. 127). Из-

вестно, что в рассматриваемом случае искомый

интеграл равен площади

aABb

криволинейной трапеции, основание которой –

отрезок оси

,Ox

а сверху она ограничена кривой с уравнением

( ).y fx=

Разделим интервал на равных частей длины число за-

дадим по нашему усмотрению. Обозначим Определим точки де-

ления Вычислим в них

значения подинтегральной функции, которые обозначим

() ,fx y=

( ) , ...,fx y=

() ,

fx y

−−

() .

fx y=

Эти числа представляют собой ординаты

точек кривой

,AB

абсциссы которых есть соответственно

012 1

, , , ... , , .

xxx x x

−

Обозначим точки

( ) ( ) ( ) ( ) ( )

000 111 222 1 1 1

, , , , , ,..., , , , .

n n n nnn

M xy Mxy M xy M x y M xy

−−−

Каждые две соседние из них соединим хордой. Получим фигуру, состоящую

из

трапеций, высоты которых одинаковы и равны

.x∆

Длины оснований

трапеций равны

012 1

, , , ..., , .

yyy y y

−

Площадь фигуры

, состоящей из этих

трапеций, равна сумме площадей трапеций:

( )

0 12 1

( )/2 ... .

nn n

S xy y y y y

−

=∆ + + + ++

( )

,fx

( )

,ab<

( )

[ ]

,ab

( )

,y fx=

,axb≤≤

,Ox

,ab

[ ]

,ab

( )

,x ban∆= −

,ax=

bx=

,xa=

10 21 1 2

, ,..., , .

nn n

x x xx x x x x xx b

−−

= +∆ = +∆ = +∆ =

Рис. 127

5354.ru

230

Ясно, что найдённую площадь приближённо можно взять в качестве пло-

щади криволинейной трапеции следовательно, приближённо можно

принять ее равной искомому интегралу. В итоге получим формулу

Она называется формулой трапеций для приближённого вычисления опреде-

лённого интеграла. Чем больше число делений тем формула точнее. Пред-

лагаем самостоятельно, использовав ее, вычислить интеграл взяв

6.n =

aABb

( )

12 1

... , .

f x dx x y y y x

−



≈∆ + + + + ∆ =





∫

sin ,xdx

∫