Сафарбаков А.М., Лукьянов А.В., Пахомов С.В. Основы технической диагностики деталей и оборудования. Часть 1
Подождите немного. Документ загружается.


61
х
3
,
а
также
признаки
х
6
и
х
7
.
В
первой
группе
более
сложно
контролируе
-
мым
является
признак
х
3
,
а
во
второй
–
признак
х
7
.
Именно
эти
два
призна
-
ка
и
должны
быть
вычеркнуты
.
Вычеркнутые
строки
(
а
соответственно
–
вычеркнутые
признаки
)
из
дальнейшего
рассмотрения
исключаются
.
По
результатам
первого
этапа
формируется
сокращенная
таблица
(
табл
. 4.3).
На втором этапе
путем
последовательного
условного
разбиения
со
-
кращенной
таблицы
(
матрицы
)
на
ряд
более
мелких
таблиц
(
подматриц
)
выполняется
отбор
необходимого
и
достаточного
количества
признаков
.
Речь
идет
о
последовательном
условном
разбиении
предыдущей
таблицы
.
При
каждом
разбиении
определяется
самый
информативный
признак
,
включаемый
в
искомую
группу
минимально
необходимых
и
достаточных
признаков
.
Условное
разбиение
исходной
матрицы
на
подматрицы
осуществля
-
ется
в
следующей
последовательности
:
1.
В
исходной
матрице
устанавливается
и
фиксируется
наиболее
ин
-
формативный
признак
(
в
нашем
примере
это
х
6
) (
см
.
табл
. 4.3).
2.
Рассматривая
строку
наиболее
информативного
и
зафиксирован
-
ного
признака
,
выявляют
состояния
,
на
которые
данный
признак
реагирует
(
в
нашем
примере
это
S
2
, S
4
и
S
5
),
а
также
на
какие
не
реагирует
(
в
нашем
примере
это
S
1
и
S
3
) (
см
.
табл
. 4.3).
3.
Состояния
,
на
которые
наиболее
информативный
признак
реаги
-
рует
(
в
нашем
примере
это
S
2
, S
4
и
S
5
),
образуют
столбцы
правой
подмат
-
рицы
(
табл
. 4.4).
Строки
правой
подматрицы
образуют
те
признаки
,
кото
-
рые
реагируют
хотя
бы
на
одно
из
указанных
в
столбце
состояний
(
в
на
-
шем
примере
это
X
2
, X
4
и
X
8
).
Элементами
правой
подматрицы
являются
единицы
или
нули
,
переписываемые
из
исходной
матрицы
(
см
.
табл
. 4.3)
и
стоящие
в
ней
на
пересечении
соответствующих
строк
и
столбцов
.
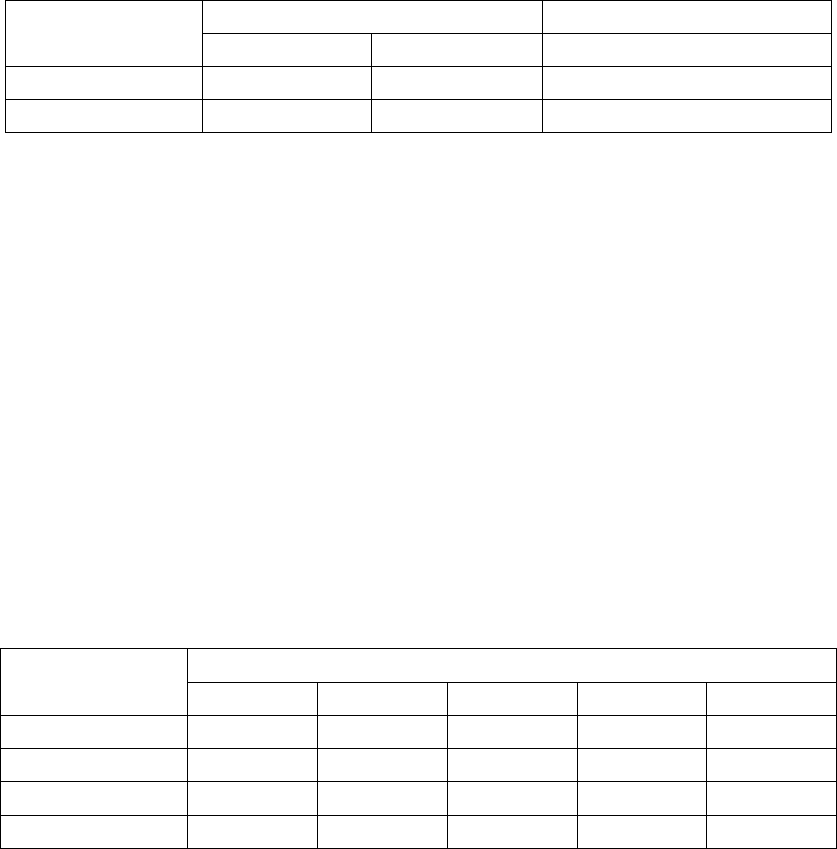
Таблица
4.4
Состояния
Информативность
Параметры
S
2
S
4
S
5
Zx
i
X
2
1 0 0 2
X
4
1 1 1 0
X
8
0 1 0 2
4.
Состояния
,
на
которые
выделенный
ранее
параметр
не
реагирует
(
в
нашем
примере
это
S
1
и
S
3
),
образуют
столбцы
левой
подматрицы
(
табл
.
4.5).
Строки
левой
подматрицы
образуют
те
параметры
,
которые
реагиру
-
ют
хотя
бы
на
одно
из
указанных
в
столбцах
состояние
(
в
нашем
примере
это
х
1
и
х
4
).
Элементами
левой
подматрицы
являются
единицы
или
нули
,
переписываемые
из
соответствующих
мест
исходной
матрицы
(
см
.
табл
.
4.3).
62
5.
Для
каждого
параметра
в
левой
и
правой
подматрицах
рассчиты
-
ваются
показатели
информативности
параметров
(
отдельно
для
каждой
подматрицы
):
ii
l
i
iX
nmZ
i
)(
1
⋅=
∑
=
,
где
l –
количество
подматриц
,
в
которые
включен
рассматриваемый
при
-
знак
x
i
; m
i
–
количество
единиц
в
каждой
i-
й
подматрице
по
рассматривае
-
мому
признаку
x
i
; n
i
–
количество
нулей
в
каждой
i-
й
подматрице
по
рас
-
сматриваемому
признаку
x
i
.
Таблица
4.5
Состояния
Информативность
Параметры
S
1
S
3
Zx
i
X
1
1 0 1
X
4
1 0 1
Рассчитанные
значения
Ix
i
и
Zx
i
по
каждому
признаку
вписываются
в
соответствующие
строки
и
столбцы
подматриц
,
так
как
это
показано
в
табл
. 4.4
и
4.5.
6.
Условно
считая
каждую
ранее
полученную
подматрицу
за
исход
-
ную
матрицу
,
повторяются
(
для
каждой
подматрицы
отдельно
)
все
дейст
-
вия
по
пунктам
1...5.
Итеративное
(
повторяющееся
)
дробление
на
подмат
-
рицы
повторяется
до
тех
пор
,
пока
реагирование
или
не
реагирование
того
или
иного
признака
однозначно
не
укажет
на
строго
определенное
состоя
-
ние
контролируемого
объекта
.
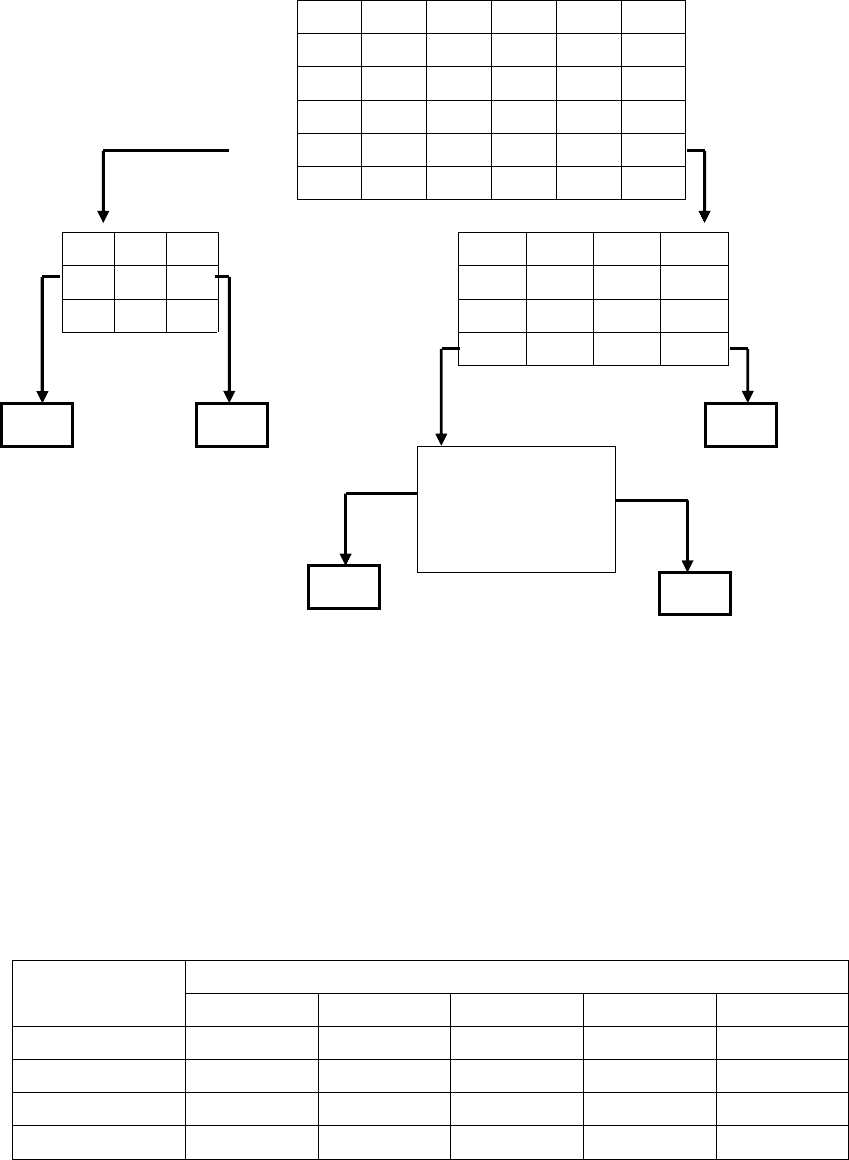
Пример
такого
«
ветвящегося
»
от
исходной
матрицы
процесса
дробления
представлен
на
рис
.4.5.
7.
Решение
задачи
прекращается
,
как
только
путем
выделения
и
фик
-
сирования
наиболее
информативных
признаков
будут
однозначно
указаны
все
состояния
контролируемого
объекта
.
Таблица
4.6
Состояния
Параметры
S
1
S
2
S
3
S
4
S
5
X
1
– +
X
2
– +
X
6
+ – + – –
X
8
+ – +
Третий
этап
является
завершающим
.
На
этом
этапе
анализируются
и
оформляются
результаты
выполнения
первых
двух
этапов
.
Оформление
результатов
заключается
в
заполнении
итоговой
таблицы
.
Все
состояния
контролируемого
объекта
образуют
столбцы
(
в
нашем
примере
это
S
1
, S
2
,
63
S
3
, S
4
, S
5
).
Все
наиболее
информативные
признаки
,
выявленные
на
втором
этапе
,
образуют
строки
итоговой
таблицы
(
табл
. 4.6) (
в
нашем
примере
это
х
1
, х
2
, х
6
, х
8
).
Элементами
итоговой
таблицы
,
проставляемыми
на
пересече
-
нии
столбцов
и
строк
,
являются
символы
«+»
или
«–».
Эти
символы
могут
быть
легко
проставлены
,
если
воспользоваться
рис
.4.5.
S
1
S
2
S
3
S
4
S
5
X
1
1 0 0 0 0
X
2
0 1 0 0 0
X
4
1 1 0 1 1
X
6
0 1 0 1 1
X
8
0 0 0 1 0
+ –
S
1
S
3
S
2
S
4
S
5
X
1
1 0
X
2
1 0 0
X
4
1 0 X
4
1 1 1
X
8
0 1 0
+ – + –
+ –
Примечание: «+» – если при проверке параметра он в норме; «–» – не в норме
Рис. 4.5. Схема выявления состояний
На
завершающем
этапе
оформляют
матрицу
кодов
,
которую
можно
понимать
и
как
искомую
группу
контролируемых
параметров
,
и
как
алго
-
ритм
(
в
матричном
виде
)
поиска
места
отказа
в
объекте
диагностирования
(
табл
.4.7).
Таблица
4.7
Состояния
Параметры
S
1
S
2
S
3
S
4
S
5
X
1
– + + + +
X
2
+ – + + +
X
6
+ – + – –
X
8
+ + + – +
S
3
S
1
S
2
S
5
X
2
1 0
X
4
1 1
S
4
S
5
S
2
64
Рассмотренные
процедуры
формирования
достаточного
набора
кон
-
тролируемых
параметров
позволяют
заключить
:
-
подход
И
.
М
.
Синдеева
позволяет
уменьшить
до
минимума
число
контролируемых
параметров
(
с
7
до
4);
-
достаточное
число
контролируемых
параметров
оказалось
меньше
числа
состояний
объекта
,
что
возможно
благодаря
комплексному
исполь
-
зованию
результатов
замера
параметров
при
диагностировании
объекта
;
-
таблица
кодов
представляет
эффективный
алгоритм
поиска
места
отказа
в
системе
.
Так
,
при
наличии
отказа
в
системе
необходимо
замерить
четыре
па
-
раметра
(X
1
, X
2
, X
6
и
X
8
).
Если
параметр
X
1
окажется
не
в
норме
,
а
три
дру
-
гие
параметра
(X
2
, X
6
и X
8
) –
в
норме
,
то
произошло
событие
S
1
(
отказ
блока
№
1).
Если
после
замеров
четырех
параметров
параметры
X
1
и
X
8
окажутся
в
норме
,
а
параметры
X
2
и
X
6
–
не
в
норме
,
то
произошло
событие
S
2
-
отказ
блока
№
2
и
т
.
д
.
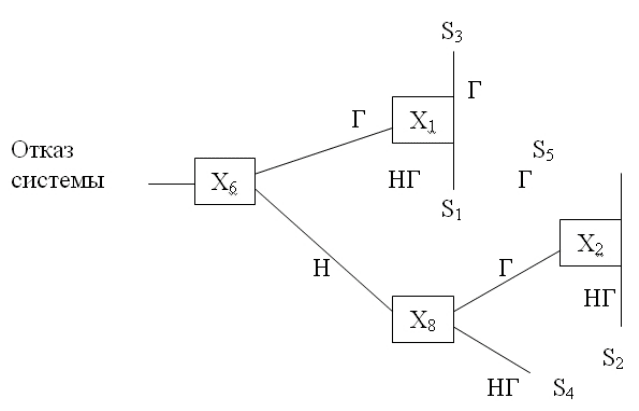
Необходимо
отметить
,
что
в
соответствии
с
ГОСТом
алгоритмы
по
-
иска
места
отказа
обычно
оформляют
в
виде
графической
схемы
.
Пример
такой
схемы
алгоритма
представлен
на
рис
.4.6.
Рис. 4.6. Схема алгоритма поиска места отказа:
Г – проверяемый параметр «годен» (соответствует требованиям документации); НГ –
проверяемый параметр «не годен»;
х
i
– i-ый проверяемый параметр;
S
j
– отказ j-ой
сборочной единицы (агрегата).
65
ГЛАВА 5. МЕТОДЫ И ПРОГРАММЫ ПОИСКА МЕСТА ОТКАЗА
Если
контроль
работоспособности
объекта
дает
отрицательный
ре
-
зультат
,
то
возникает
задача
определения
места
отказа
с
заданной
подроб
-
ностью
(
точностью
)
до
съемного
блока
,
съемной
платы
в
блоке
,
отдельно
-
го
элемента
в
схеме
.
Как
правило
,
процесс
поиска
места
отказа
имеет
большую
длительность
и
трудоемкость
,
требует
специальных
средств
ди
-
агностирования
.
Они
зависят
от
того
,
насколько
хорошо
построен
сам
этот
процесс
,
каким
выбран
алгоритм
диагностирования
.
Алгоритмом диагностирования
называется
совокупность
предписа
-
ний
о
порядке
проведения
диагностирования
(
ГОСТ
20911-75).
Он
задает
совокупность
элементарных
проверок
,
их
последовательность
,
правила
их
реализации
и
правила
обработки
результатов
контроля
.
5.1. Программы поиска места отказа
5.1.1. Общие понятия и классификация программ
Если
при
эксплуатации
оборудования
сетей
железных
дорог
или
при
проверке
их
работоспособности
установлен
факт
неработоспособности
,
то
чаще
всего
возникает
необходимость
в
поиске
места
отказа
и
выявлении
его
последствий
.
Опыт
эксплуатации
свидетельствует
,
что
из
перечислен
-
ных
мероприятий
наиболее
трудоемким
и
интеллектоемким
является
по
-
иск
места
отказа
.
В
среднем
на
это
затрачивается
до
90 %
времени
,
связан
-
ного
с
проведением
всего
комплекса
мероприятий
по
отказу
.
В
этой
связи
особое
значение
приобретает
формирование
у
специалистов
по
системам
обеспечения
движения
поездов
знаний
и
навыков
по
научно
обоснован
-
ным
методам
программирования
процессов
поиска
мест
отказов
.
Под
программой
поиска
места
отказа
понимают
заранее
состав
-
ленную
и
документально
оформленную
последовательность
элементарных
проверок
(
замеров
контролируемых
параметров
)
и
последовательность
анализа
результатов
элементарных
проверок
,
выполняемых
с
целью
уста
-
новления
причины
отказа
и
отказавших
агрегатов
(
узлов
,
систем
,
элемен
-
тов
и
т
.
д
. –
в
зависимости
от
степени
детальности
поиска
мест
отказа
).
Из
всех
возможных
вариантов
программ
всегда
имеется
такой
,
кото
-
рый
является
оптимальным
с
точки
зрения
используемого
критерия
.
В
ка
-
честве
критерия
оптимальности
программы
поиска
места
отказа
могут
быть
использованы
:
•
суммарное
время
выполнения
необходимых
проверок
;
•
суммарное
количество
необходимых
проверок
;
•
суммарная
стоимость
проверок
(
например
,
в
денежном
выражении
);
•
суммарная
стоимость
(
или
суммарная
масса
)
контрольно
-
поверочной
аппаратуры
,
задействованной
для
выполнения
необходимых
прове
-
66
рок
.
Следует
отметить
,
что
в
практике
специалистов
АТС
и
ЭНС
наи
-
большее
распространение
получил
такой
критерий
оптимальности
про
-
грамм
поиска
места
отказа
,
как
суммарное
время
выполнения
необходи
-
мых
проверок
t
∑
.
В
соответствии
с
этим
критерием
программа
строится
та
-
ким
образом
,
чтобы
обеспечить
минимальное
суммарное
время
на
выявле
-
ние
места
отказа
,
то
есть
)min(
1
∑
=
∑
=
K
i
i
tt ,
где
t
i
–
время
выполнения
i-
ой
элементарной
проверки
; K –
максимальное
число
элементарных
проверок
для
выявления
места
отказа
в
объекте
.
Понятно
,
что
при
наличии
нескольких
вариантов
программ
поиска
места
отказа
выбирается
тот
,
который
обеспечивает
меньшую
величину
критерию
t
∑
.
Если
же
и
таких
вариантов
несколько
,
то
предпочтение
отда
-
ется
такой
программе
,
которая
обеспечивает
лучшие
значения
другим
кри
-
териям
(
например
,
суммарному
количеству
необходимых
элементарных
проверок
).
В
связи
с
разнообразием
видов
оборудования
железных
дорог
,
рас
-
полагаемых
контрольно
-
проверочных
средств
,
а
также
эксплуатационных
условий
,
в
практике
АТС
и
ЭНС
применяются
несколько
разновидностей
программ
поиска
места
отказа
.
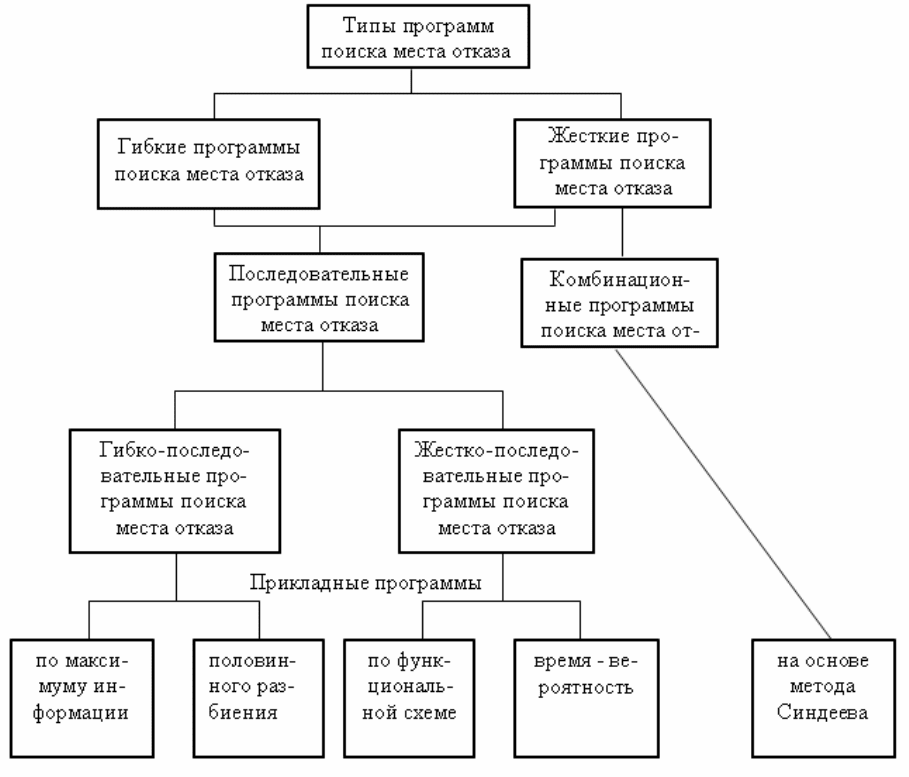
Классификация
программ
.
Один
из
возможных
вариантов
класси
-
фикации
программ
поиска
места
отказа
представлен
на
рис
.5.1.
В
соответ
-
ствии
с
рисунком
все
типы
программ
по
способу
выбора
контролируемых
параметров
и
последовательности
элементарных
проверок
условно
разгра
-
ничиваются
на
две
группы
:
жесткие
программы
и
гибкие
программы
.
В
жестких
программах
последовательность
элементарных
прове
-
рок
определяется
заранее
,
и
в
ходе
поиска
места
отказа
не
изменяется
.
Кроме
того
,
заранее
должен
быть
определен
и
перечень
параметров
,
кон
-
тролируемых
в
каждой
элементарной
проверке
.
Жесткие
программы
получили
наибольшее
распространение
в
авто
-
матических
и
в
автоматизированных
системах
контроля
.
В
гибких
программах
последовательность
элементарных
проверок
определяется
в
ходе
поиска
места
отказа
на
основе
определенных
правил
.
Кроме
того
,
перечень
параметров
,
контролируемых
в
каждой
элементар
-
ной
проверке
,
формируется
только
после
анализа
результатов
предыдущей
элементарной
проверки
.
Таким
образом
,
программа
(
алгоритм
)
формиру
-
ется
«
гибко
»,
максимально
приспосабливаясь
к
специфике
каждого
кон
-
кретного
отказа
АТ
.
Гибкие
программы
наибольшее
распространение
получили
при
по
-
иске
места
отказа
способом
технического
осмотра
(
т
.
е
.
визуально
-
инструментально
,
группой
специалистов
АТС
и
ЭНС
).
67
Все
типы
программ
по
частоте
анализа
результатов
элементарных
проверок
условно
разграничивают
на
две
группы
:
последовательные
про
-
граммы
и
комбинационные
программы
.
Рис.5.1. Классификация программ поиска места отказа
В
последовательных
программах
анализ
результатов
проводится
после
каждой
элементарной
проверки
.
В
комбинационных
программах
–
только
после
завершения
всех
элементарных
проверок
,
когда
проводится
единственный
обобщающий
анализ
.
Необходимо
отметить
,
что
в
практике
АТС
и
ЭНС
наибольшее
распространение
получили
последовательные
программы
.
Что
касается
комбинационных
программ
,
то
они
представлены
одним
типом
прикладной
программы
– «
программой
на
основе
метода
Синдеева
»,
рассмотренного
ранее
,
где
она
использовалась
не
как
инстру
-
мент
для
поиска
места
отказа
,
а
как
инструмент
выбора
минимально
необ
-
ходимого
набора
контролируемых
параметров
.
Наиболее
распространенные
программы
поиска
места
отказа
условно
разграничивают
на
две
группы
:
гибко
-
последовательные
(
к
ним
относят
: «
программу
по
максимуму
68
информации
»
и
«
программу
половинного
разбиения
»);
жестко
-
последовательные
(
к
ним
относят
: «
программу
по
функ
-
циональной
схеме
»
и
«
программу
время
-
вероятность
»).
5.2. Жестко-последовательные программы
5.2.1. Программы по функциональной схеме
Программа
по
функциональной
схеме
основана
на
поиске
места
от
-
каза
путем
выполнения
в
«
жестком
»
порядке
(
строго
по
функциональной
схеме
отказавшей
системы
,
например
,
в
порядке
передачи
от
элемента
к
элементу
механической
нагрузки
или
в
направлении
движения
жидкости
)
последовательных
элементарных
проверок
.
Результаты
каждой
элементар
-
ной
проверки
сразу
же
анализируются
.
Элементарной
проверке
подлежит
диагностический
параметр
(
пара
-
метры
)
каждого
отдельного
элемента
системы
.
Поиск
места
отказа
пре
-
кращается
,
как
только
при
анализе
результатов
очередной
элементарной
проверки
окажется
найденным
отказавший
элемент
системы
.
Очевидно
,
что
в
самом
неблагоприятном
случае
(
когда
отказал
последний
из
прове
-
ряемых
элемент
системы
)
число
элементарных
проверок
будет
максималь
-
ным
и
равным
числу
элементов
в
системе
.
Достоинствами
рассмотренной
программы
являются
:
•
возможность
использования
для
новой
техники
,
когда
не
накоплен
опыт
ее
эксплуатации
,
и
тем
более
–
когда
не
накоплены
статистиче
-
ские
данные
по
поиску
мест
ее
отказов
;
•
простота
,
доступность
для
широкого
круга
специалистов
АТС
и
ЭНС
.
К
недостаткам
программы
следует
отнести
:
•
необходимость
выполнения
большого
количества
элементарных
про
-
верок
,
что
требует
больших
затрат
времени
и
материальных
ресурсов
;
•
необходимость
использования
при
поиске
мест
отказов
помимо
спе
-
циалистов
и
КПА
еще
и
эксплуатационной
документации
(
техниче
-
ского
описания
,
инструкции
по
технической
эксплуатации
,
альбома
формулярных
схем
и
т
.
д
.).
Несмотря
на
отмеченные
недостатки
, «
программа
по
функциональ
-
ной
схеме
»
нашла
у
специалистов
ЭНС
и
АТС
,
пожалуй
,
самое
широкое
распространение
прежде
всего
из
-
за
своей
простоты
,
доступности
широ
-
кому
кругу
специалистов
(
независимо
от
их
опыта
эксплуатации
,
в
опреде
-
ленной
степени
, –
от
их
квалификации
).
5.2.2. Программы «вероятность»
–
«время»
Программа
«
вероятность
» – «
время
»
может
быть
использована
лишь
тогда
,
когда
по
отказам
данного
типа
обрудования
уже
накоплен
и
систе
-
матизирован
достаточно
большой
опыт
ее
эксплуатации
,
и
,
в
частности
,
опыт
поиска
места
отказа
.
Прежде
всего
,
по
каждому
элементу
системы
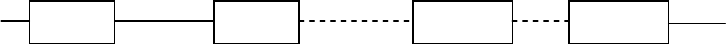
69
должны
быть
известны
:
•
вероятность
отказа
i-
го
элемента
q
i
;
•
время
,
необходимое
для
элементарной
проверки
i-
го
элемента
τ
i
.
Программа
«
вероятность
–
время
»
основана
на
поиске
места
отказа
путем
выполнения
в
«
жестком
»
порядке
(
строго
в
порядке
убывания
чис
-
ленных
значений
отношения
qi/τ
i
)
последовательных
элементарных
прове
-
рок
элементов
.
Элементарной
проверке
подлежит
диагностический
пара
-
метр
(
параметры
)
каждого
отдельного
элемента
системы
.
Результаты
каж
-
дой
элементарной
проверки
сразу
же
анализируются
.
Поиск
места
отказа
прекращается
,
как
только
при
анализе
результатов
очередной
элементар
-
ной
проверки
окажется
найденным
отказавший
элемент
системы
.
Очевидно
,
что
такая
программа
позволяет
в
первую
очередь
прове
-
рять
те
элементы
отказавшей
системы
,
вероятность
отказа
которых
наи
-
большая
,
а
время
на
элементарную
проверку
–
наименьшее
.
В
результате
этого
общее
время
на
выявление
места
отказа
системы
оказывается
суще
-
ственно
меньше
,
чем
при
использовании
ранее
рассмотренной
программы
по
функциональной
схеме
.
Покажем
это
на
примере
системы
,
изображенной
на
рис
.5.2
и
содер
-
жащей
N
последовательно
соединенных
элементов
.
Один
из
элементов
от
-
казал
,
что
привело
к
отказу
всей
системы
.
Рис.5.2. Схема системы из последовательно соединенных элементов
Пусть
по
каждому
i-
му
элементу
системы
известны
численные
зна
-
чения
вероятности
его
отказа
q
i
и
времени
на
его
элементарную
проверку
τ
i
.
Для
начала
назначим
произвольную
программу
поиска
места
отказа
(
то
есть
произвольный
порядок
выполнения
элементарных
проверок
),
напри
-
мер
,
в
соответствии
с
нумерацией
элементов
на
рисунке
.
В
этом
случае
математическое
ожидание
времени
поиска
места
отка
-
за
составит
)...(...)()(
2121211
NNI
qqqtM
τ
τ
τ
τ
τ
τ
+
+
+
⋅
+
+
+
⋅
+
⋅
=
∑
. (5.1)
Теперь назначим второй вариант программы поиска места отказа,
отличающийся от первого варианта тем, что вначале проверяется второй
элемент, затем первый, а последующие элементарные проверки выполня-
ются в такой же последовательности, как и в первом варианте (в порядке
нумерации).
Для второго варианта программы математическое ожидание времени
поиска места отказа составит
)...(...)()(
1212122
NNII
qqqtM
τ
τ
τ
τ
τ
τ
+
+
+
⋅
+
+
+
⋅
+
⋅
=
∑
. (5.2)
Если вычесть из M(t
∑
)
І
величину M(t
∑
)
П
,
то после выполнения ариф-
1
2
i
N

70
метических действий получим
2112
)()(
τ
τ
⋅
−
⋅
=
−
∑∑
qqtMtM
III
. (5.3)
Из анализа полученной разности следует, что первый вариант про-
граммы будет эффективнее (исходя из затрат времени на поиск места отка-
за) второго варианта лишь в том случае, когда
0
2112
<
⋅
−
⋅
τ
τ
qq ,
то есть
2112
τ
τ
⋅
>
⋅
qq , или иначе
2
2
1
1
ττ
qq
> . (5.4)
Таким образом, упорядочив элементарные проверки элементов в со-
ответствии с выражением
N
N
i
i
qq
qq
ττττ
......
2
2
1
1
>>> , (5.5)
мы получим оптимальную программу поиска места отказа, обеспечиваю-
щую минимальную величину математического ожидания времени поиска
места отказа. Правило (5.5) положено в основу программ «вероятность» –
«время».
После расчета (для всех элементов) отношений qi/τ
i
устанавливают
порядок проверки элементов. Этот порядок соответствует порядку ранжи-
рования отношения qi/τ
i
(в порядке убывания). Программа этого типа вы-
глядит как последовательность номеров элементов объекта в порядке их
проверки.
Рассмотрим пример практического составления и использования
программы «вероятность» – «время». Пусть требуется составить програм-
му поиска места отказа в системе, состоящей из пяти элементов (рис.5.3).
То есть требуется указать оптимальный порядок проведения элементарных
проверок элементов.
Рис.5.3. Пример пятиэлементной системы
Из опыта эксплуатации известно, что за 23 случая применения дан-
ной системы происходили отказы элементов, указанные в таблице 5.1.
Решение задачи начинается с расчета для каждого элемента величи-
ны
q
i
(она определяется как отношение числа отказов элемента n
i
к числу
применения системы). Затем для каждого элемента рассчитывается вели-
чина q
i/
τ
i
.
По численным значениям
q
i/
τ
i
проводим новую нумерацию элементов
системы (в порядке убывания значений q
i/
τ
i
). Эта новая нумерация указана в
последней строке таблицы, и она определяет искомый порядок выполнения
элементарных проверок элементов в рассматриваемой системе.
1
2
4
5
3
