Садчикова Г.М. Цикловые дискретные системы управления

Подождите немного. Документ загружается.

Министерство образования и науки Российской Федерации

Саратовский государственный технический университет

Балаковский институт техники, технологии и управления

МОДЕЛИРОВАНИЕ РАБОТЫ ЦИКЛОВЫХ ДИСКРЕТНЫХ

СИСТЕМ УПРАВЛЕНИЯ АВТОМАТАМИ

Методические указания

к выполнению лабораторной работы по курсу

“Моделирование процессов в машиностроении”

для студентов специальности 120100

дневной, вечерней и заочной форм обучения

Одобрено

редакционно-издательским советом

Балаковского института техники,

технологии и управления

Балаково 2005

ЦЕЛЬ РАБОТЫ: ознакомиться с основами моделирования цикловых

дискретных систем управления, с операциями и законами теории

дискретных автоматов, формами записи релейных (логических функций).

Научиться на основе переключательной функции составлять циклограммы

работы дискретных систем, таблицу включений и структуру

управляющего автомата.

1. ОСНОВНЫЕ ПОНЯТИЯ

Устройства дискретного действия, выполненные на элементах гидро-,

пневмо- и электроавтоматики, и управляющие микропроцессоры в

настоящее время широко применяют для управления самыми различными

станками, автоматами, роботами и автоматическими линиями. Обычно

системы управления автоматов являются многотактными дискретными

устройствами. Основой построения многотактного дискретного автомата

являются, прежде всего, условия взаимодействия с объектом управления,

т. е. порядок поступления входных сигналов и требования к выдаваемым

сигналам. Такие устройства называют релейными.

Теория дискретных автоматов (ТДА) — теория построения структуры

релейных устройств — решает три основные задачи: синтеза, то есть

получения структуры релейного устройства по заданным для нее условиям

работы (например, циклограмм, таблиц включения, заданной

последовательности во времени срабатывания элементов устройства и т.д.);

минимизации и анализа, т. е. определение для уже готовой структуры

устройства условий ее работы (например, определение последовательности

действующих во времени сигналов, выявление действия устройства при

повреждении и т. д.).

Практическое применение ТДА значительно сокращает время

разработки структуры устройства и получения более совершенных

схемных решений.

Под устройством релейного (дискретного) действия (УРД) или под

дискретным автоматом понимают устройство, перерабатывающее или

распределяющее по заданной программе информацию, поступающую и

выдаваемую в виде дискретных сигналов. Основной особенностью УРД

является то, что состояние его выходов меняется скачкообразно при

соответствующих изменениях параметра входного сигнала X, на который

должно реагировать данное УРД. УРД по принципу работы их элементов во

времени разделяются на два класса: однотактные и многотактные.

Однотактные (комбинационные схемы): выходной сигнал зависит

только от комбинации сигналов на входе схемы в данный момент времени

(рис. 1).

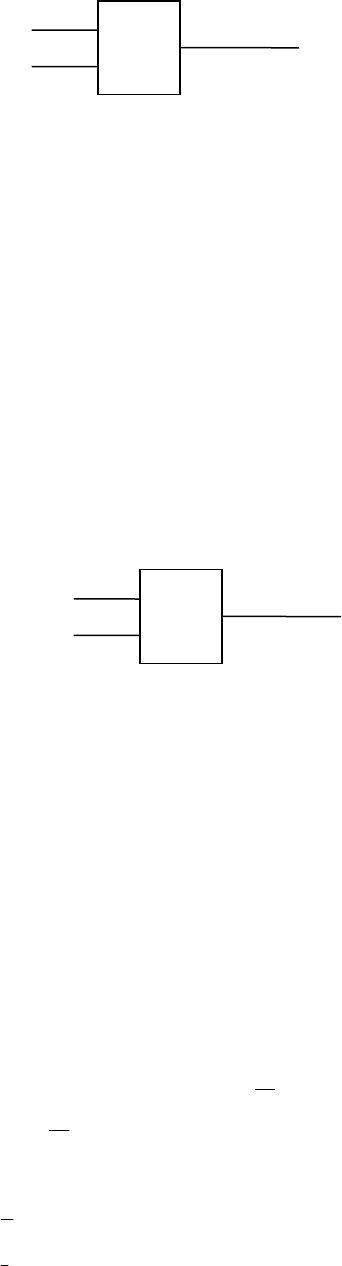
Рис. 1. Комбинационная схема

Схема не содержит элементов памяти, и сигналы, поступающие на

вход, не сохраняются.

Многотактные (цифровые автоматы) - схемы с памятью (рис. 2). Слово

на выходе цифрового автомата в каждый дискретный момент времени t

определяется комбинацией входных сигналов, поступивших в момент t на

вход автомата и внутренним состоянием автомата, которое установилось в

результате воздействия на автомат входных сигналов в предыдущие

дискретные моменты t.

Рис. 2. Цифровой автомат

К С

х 1

х 2

х n

y = f ( x 1 , x 2 . . . x n )

Ц А

х 1

х 2

х n

y = f ( x 1 , x 2 . . . x n , Q )

t - 1

Математический аппарат, который отображает функционирование

дискретных автоматов, называется алгеброй релейных цепей или алгеброй

логики.

1.1. Алгебра релейных цепей

Величины, описывающие состояние дискретного автомата, являются

переменными, хотя принимают только два различных значения. Такая

переменная величина может представлять собой либо изменение состояния

какого-нибудь конкретного элемента дискретного автомата, либо

изменение состояния, происходящее в результате работы группы

элементов.

Переменные не имеют численного значения. Можно сказать, что цепь

замкнута или разомкнута, но нельзя ответить на вопрос, насколько она

замкнута или разомкнута. Таким образом, когда говорят, что некоторая

переменная двузначна, то это не значит, что она принимает два значения в

обычном смысле, т. е. принимает значения, например, 1,05 и 1,06. Это

означает, что эта переменная характеризует два качественных состояния

элемента или системы элементов. При интерпретации результатов

алгебраических преобразований удобно иметь возможность приписывать

«значения» переменным. В частности, если известны значения, которые

характеризуют состояния отдельных элементов устройства, то алгебра

релейных цепей позволяет определить значение, характеризующее

состояние всего устройства в целом.

В качестве двух значений переменных удобно принимать цифры 0 и 1.

Например, цифра 0 может представлять либо замкнутую, либо

разомкнутую цепь, а тогда цифра 1 может представить соответственно

разомкнутую или замкнутую цепь. В алгебре релейных цепей цифры 0 и 1

представляют только условие работы или состояние релейных элементов.

Эти цифры не дают никакой количественной оценки их свойств, и поэтому

их не следует рассматривать как числа в обычном смысле. При помощи

алгебры релейных цепей решают две задачи теории дискретных автоматов:

анализ релейных устройств; синтез релейных устройств.

Над переменными алгебры релейных цепей можно производить ряд

операций, которые сводятся к трем основным: операция НЕ, операция

ИЛИ, операция И.

Операция НЕ (логическое отрицание, инверсия). Запись

переключательной функции (читается: Y есть инверсия от А):

AAf(A)y 

Отрицанием высказывания А называется операция, результат которой

Y истинен, когда А ложно, и ложен, когда А истинно, другими словами,

сигнал на выходе равен «1», если сигнал на входе равен «0».

В электрических схемах данную операцию реализует логический

элемент НЕ (инвертор) (рис. 3). Сигнал на выходе инвертора появляется

при его отсутствии на входе, и наоборот.

Рис. 3. Условное обозначение инвертора

Операция ИЛИ (логическое сложение, дизъюнкция).

BAB)f(A,y 

Дизъюнкция — это логическая операция над двумя и более

переменными, результат которой истинен, если хотя бы одна из

составляющих его переменных истинна. В электрических схемах

операцию логического сложения выполняет дизъюнктор (собирательная

схема) (рис. 4). Сигнал на выходе дизъюнктора появляется в том случае,

если подан сигнал хотя бы на один из его входов. Операция ИЛИ

y =A

справедлива при любом числе логических переменных.

Рис. 4. Условное обозначение дизъюнктора

Операция И (логическое умножение, конъюнкция).

У =f(A,B)=AB=A*B

Конъюнкция — это логическая операция над двумя и более

переменными, результат которой истинен, если истинны значения всех

переменных. В электрических схемах логическое умножение выполняет

схема И (схема совпадения, конъюнктор) (рис. 5). На выходе конъюнктора

появляется сигнал только в том случае, если есть сигналы на всех его

входах.

Рис. 5. Условное обозначение конъюнктора

Операция И справедлива при любом числе логических переменных.

1.2. Постулаты алгебры релейных цепей

Как и любая алгебра, алгебра релейных цепей строится на аксиомах и

законах. Аксиомы (тождества) алгебры релейных цепей, а именно:

Y = AB

Y = AB

0.XX

X;XX

X;1X



0;1

1;0

0;0X

1;XX

X;XX

1;1X

X;0X







Коммутативный закон (переместительный закон):

Х  Y = Y  X;

XY = YX

Ассоциативный закон (сочетательный закон):

(X  Y)  Z = Х  (Y  Z);

(XY)Z = X(YZ) = XYZ.

Дистрибутивный закон (распределительный закон):

Х  YZ = (X  Y)(X  Z);

X(Y  Z) = XY  XZ.

Закон инверсии (правило де Моргана, закон двойственности):

 

.YXYX

;YXYX





Правила и следствия из основных законов алгебры релейных цепей

1. Правило поглощения

XXY = X(1Y) = X;

Х(ХY) = XX  XY = Х  XY = Х(1Y) = X.

2. Правило склеивания

 

X.YYXYXYX

X;YYXYXXY





Некоторые законы можно обобщить на случаи большего числа

переменных. Например, правило де Моргана:

 

.Z...YXZ...YX

;Z...YXZ...YX





Закон дистрибутивности:

XY…Z = (X)(Y)…(Z);

(XY…Z) = X  Y … Z.

1.3. Формы записи релейных (логических) функций

Логические функции могут быть представлены либо в аналитической,

либо в табличной форме. Табличная форма записи представляет собой

таблицу истинности. Таблица истинности - это таблица, содержащая все

возможные комбинации входных переменных и соответствующие им

значения выходных переменных, то есть значения функции (табл. 1).

Таблица 1

Таблица истинности

А В f(A, В)

0 0 f(0, 0)

0 1 f(0, 1)

1 0 f(1, 0)

1 1 f(1, 1)

В аналитической форме записи функция представляет собой формулу,

состоящую из булевых констант и переменных, связанных операциями И,

ИЛИ, НЕ. Пример:

ABC.B)A)(B(AC)B,f(A, 

Для перехода от аналитической формы записи к таблице истинности

нужно подставить в формулу значения входных переменных и вычислить

значение функции.

При аналитическом описании логических функций используются

понятия элементарной конъюнкции и элементарной дизъюнкции.

Элементарная конъюнкция (минтерм, конституента единицы) - это

конъюнкция, которая связывает только отдельные переменные в прямом

или инверсном виде, например

D.A BC,A

Элементарная дизъюнкция (макстерм, конституента нуля) - это

дизъюнкция, которая связывает только отдельные переменные в прямом

или инверсном виде, например

.DA ,CBA 

Минтерм принимает единичное значение только при одном из всех

возможных наборов аргументов, а макстерм - при всех возможных наборах

аргументов, кроме одного. Число переменных, составляющих

элементарную конъюнкцию или дизъюнкцию, называется её рангом,

например, элементарная конъюнкция четвертого ранга:

CD;BAD)C,B,P(A, 

элементарная дизъюнкция третьего ранга:

.CBAC)B,M(A, 

Различают две нормальные формы записи логических функций:

дизъюнктивную нормальную форму и конъюнктивную нормальную

форму.

Дизъюнктивная нормальная форма (ДНФ) представляет собой

логическую сумму элементарных конъюнкций (минтермов), например:

C.BABAC)B,(A,f

ДНФ



Конъюнктивная нормальная форма (КНФ) представляет собой

логическое произведение элементарных дизъюнкций (макстермов),

например:

 

  

.CBABABAC)B,(A,f

КНФ



Любая логическая функция может иметь несколько дизъюнктивных и

конъюнктивных нормальных форм. Однозначность представления

логической функции выполняется при записи её в совершенных

нормальных формах.

Совершенная дизъюнктивная нормальная форма (СДНФ) логической

функции - это форма записи в виде дизъюнкции элементарных

конъюнкций, для которых значение функции равно единице. Каждая

конъюнкция, входящая в СДНФ, включает в себя каждую переменную

только один раз в прямом или инверсном виде, и все элементарные

конъюнкции имеют одинаковый ранг, например

.CABCBAABCC)B,(A,f

СДНФ



Данная функция является СДНФ, так как

 в ней нет двух одинаковых конъюнкции;

 ни одна конъюнкция не содержит двух одинаковых двоичных

переменных;

 ни одна конъюнкция не содержит двоичную переменную вместе с её

отрицанием;

 все конъюнкции одного ранга.

Совершенная конъюнктивная нормальная форма (СКНФ) логической

функции - это форма записи в виде конъюнкции элементарных

дизъюнкций, для которых значение функции равно нулю. Каждая

дизъюнкция, входящая в СКНФ, включает в себя каждую переменную

только один раз в прямом или инверсном виде, и все элементарные

дизъюнкции имеют одинаковый ранг, например

  

.CBACBAC)B,(A,f

СКНФ



1.4. Переход от таблицы истинности к СДНФ и СКНФ

Для перехода от таблицы истинности к СДНФ нужно выполнить

следующие действия:

1. Составить минтермы для тех строк таблицы истинности, на которых

функция равна единице. При этом если значение переменной в строке

равно нулю, то в минтерме она записывается со знаком отрицания.

2. Записать дизъюнкцию от составленных минтермов.

Для перехода от таблицы истинности к СКНФ нужно выполнить

следующие действия:

1. Составить макстермы для тех строк таблицы истинности, в которых

функция равна нулю. При этом переменная записывается с отрицанием,

если её значение в строке равно единице.

2. Записать конъюнкцию от составленных макстермов.

1.5. Аналитические способы перехода от нормальной к

совершенной форме логической функции

Для перехода от произвольной ДНФ i-ого ранга к СДНФ k-ого ранга

(i<k) необходимо конъюнкции, входящие в ДНФ, последовательно