Рыбалкина М. Нанотехнологии для всех

Подождите немного. Документ загружается.

www.nanonewsnet.ru

ГЛАВА 2. Законы квантового мира

случае звуковых или морских волн. Волновая функция – поня

тие чисто математическое и имеет вероятностный смысл.

Чтобы обеспечить понимание волновой функции, нам не

обходимо познакомиться сначала с основами теории вероятнос

тей. Эта тема, как правило, не входит в обычный школьный курс

математики, хотя на самом деле здесь нет ничего сложного.

Основные положения теории вероятностей

Окружающий нас мир полон случайностей. Номера выиг

рышных билетов в лотерее, количество солнечных дней в году, ре

зультаты спортивных состязаний, выпадение “решки” при подб

расывании монеты, неожиданная случайная встреча, кардинально

переворачивающая судьбу – все это примеры случайных событий,

происходящих в повседневной жизни и влияющих на нее.

Теория вероятностей не может предсказать, произойдет

или не произойдет какоето реальное событие, а лишь предла

гает математический аппарат для анализа и прогнозирования

вероятности его появления. Она изучает вероятностные зако

номерности случайных событий, существующие объективно,

т.е. независимо от наших желаний и предпочтений.

Исторически зарождение теории вероятностей связано с

поиском закономерностей в азартных играх, таких как карты и

кости. Именно тогда были предприняты первые попытки мате

матического прогнозирования и количественного определения

шансов на успех. Исходными понятиями здесь являются поня

тия “случайное событие” и “испытание” (опыт, эксперимент).

ССллууччааййннооее ссооббыыттииее

– это явление, которое при одних и тех

же условиях может или произойти, или не произойти.

ИИссппыыттааннииее

– это создание и осуществление этих неопреде

ленных условий. Любое испытание приводит к результату или

исходу, который заранее невозможно точно предсказать.

Случайные события происходят повсеместно – в природе, нау

ке, технике, экономике, военном деле и т.д. Приведем простейшие

примеры испытаний и соответствующих им случайных событий.

Важно отметить, что на самом деле “случайные события”

вовсе не случайны  просто для их расчета пришлось бы учесть

такое количество факторов и произвести расчеты такой сложнос

ти, что никто этим не занимается. Однако с совершенстованием

компьютеров и датчиков люди cмогут анализировать данные все

НАНОТЕХНОЛОГИИ ДЛЯ ВСЕХ

быстрее и точнее и многие события перестают быть случайными.

Например, попадание снаряда в цель перестало быть случайным,

когда в нем появился компьютер, рассчитывающий и корректи

рующий траекторию полета. Выигрыш в рулетку сотни лет счи

тался случайностью, пока хитрые игроки не наловчились переда

вать данные об игре через видеокамеру в суперкомпьютер, кото

рый смог рассчитать, на какую цифру упадет шарик. С развитием

нанотехнологии компьютеры станут еще мощнее и компактнее, а

значит, многие события перестанут быть случайными и станут не

только предсказуемыми, но и управляемыми.

Случайные события могут быть:

а) достоверными или невозможными;

Достоверным называется событие, которое в данных усло

виях всегда происходит, невозможным – если оно никогда не

может быть результатом данного испытания. Например, при

бросании монеты событие А – “Выпадение какойлибо сторо

ны монеты” будет достоверным, а B – “Одновременное выпа

дение “решки” и “орла”” – невозможным.

б) зависимыми или независимыми;

Если появление одного события влечет за собой появление

другого, то говорят, что второе событие зависит от первого.

в) равновероятными или неравновероятными;

Например, в случае бросания игральной кости события вы

падения каждой цифры равновероятны (если, конечно, это

“честная” кость, без смещенного центра тяжести).

А вот вероятности события “В полдень в Москве выпадет

снег” будут сильно различаться в зависимости от времени года,

соответствующего данному испытанию.

К определению самого понятия вероятности существует нес

колько различных подходов. Мы рассмотрим лишь те из них, ко

торые необходимы нам для понимания изучаемых квантовых яв

лений, а именно – классический и статистический подходы.

№№ ИИссппыыттааннииее ССооббыыттииее

1 Бросание монеты Выпадение “орла” или “решки”

2 Бросание игральной кости Выпадение 1,2,3,4,5 или 6

3 Выстрел по цели Попадание в цель или промах

4 Извлечение карты из

колоды

Извлечение карты одного цвета,

масти или достоинства

Табл 3. Примеры простейших испытаний и событий

www.nanonewsnet.ru

ГЛАВА 2. Законы квантового мира

ККллаассссииччеессккооее ооппррееддееллееннииее ввеерроояяттннооссттии

исторически сло

жилось первым. Оно имеет место в случаях, когда случайные

события являются равновероятными. Для начала рассмотрим

пример: предположим, в корзине лежат 10 шаров одинакового

размера, из которых 6 – красных, 3 – зеленых и 1 – желтый. Все

шары хорошо перемешаны, а опыт состоит в том, что мы науда

чу вытаскиваем один шар из корзины.

Результатом этого опыта будет служить одно из следующих

случайных событий w1, w2, … , w10,

где w1, w2, w3, w4, w5, w6 – выпадение красного шара

w7, w8, w9 – выпадение зеленого шара

w10 – выпадение желтого шара

Интуитивно понятно, что вероятность выпадения красно

го шара выше, чем остальных, поскольку среди всех возможных

исходов количество возможных благоприятных исходов, соот

ветствующих этому событию, выше. Таким образом,

ВВеерроояяттннооссттьь

– это отношение числа благоприятных событию

исходов m к общему числу всех равновозможных исходов n

Обычно вероятность обозначают буквой P (от англ. “prob

ability”  вероятность). Вероятность в данном случае понимает

ся как количественная мера объективной возможности появле

ния случайного события А и определяется формулой

В нашем примере событиям выпадения красного, зеленого и

желтого шара будут соответствовать вероятности 6/10, 3/10 и 1/10.

Функция вероятности обладает некоторыми специальны

ми свойствами:

1. 0<

P<1 , так как количество благоприятных исходов не

может быть больше их общего числа.

2. Вероятность достоверного события = 1

3. Вероятность невозможного события = 0

ССттааттииссттииччеессккооее ооппррееддееллееннииее ввеерроояяттннооссттии

Классическим подходом к вероятности удобно пользоваться,

когда количество всех равновозможных исходов в опыте ограни

чено и не слишком велико. Однако эти условия не всегда соблю

даются на практике: иногда приходится решать задачи, в которых

число исходов постоянно меняется или бесконечно велико. Кро

ме того, не всегда события могут быть равновероятными.

Практика показывает, что массовые случайные явления об

ладают одним уникальным свойством: с увеличением числа ис

пытаний повышается устойчивость их появления. Например,

если повторить опыт бросания монетки 100 раз, то примерно в

50% испытаний выпадет “орел”, а в 50%  “решка”. Если увели

чить число испытаний до 1000 раз, это в конце концов приведет

к еще большей устойчивости частоты полученных значений, а

это уже определенная закономерность.

При статистическом подходе нас интересует не исход отдель

но взятого испытания, а то, что получается в результате его мно

гократного повторения, то есть в качестве статистической вероят

ности события принимают частоту появления того или иного со*

бытия при неограниченном увеличении числа испытаний.

Например, если в результате достаточно большого числа

испытаний оказалось, что относительная частота весьма близка

к 0.4, то это число можно принять за статистическую вероят

ность события.

Статистический вероятностный подход используется пов

семестно для анализа и прогнозирования событий, процессов,

явлений. На его основе построены некоторые научные теории

физики, квантовой механики, эволюции, генетики, информа

тики и др. Вероятностностатистические методы широко при

меняются в промышленности для контроля качества продук

ции, технической диагностики оборудования, организации

массового обслуживания, астрономических наблюдений и т.д.

В рамках статистического подхода вводится понятие

ппллоотт**

ннооссттии рраассппррееддееллеенниияя ввеерроояяттннооссттии рр((хх)),,

вид функции которой

определяет закон распределения случайных величин. Сущест

вуют самые разные законы распределения: равномерное расп

ределение, распределение Пуассона, распределение Бернулли

и др., но наиболее распространено в природе так называемое

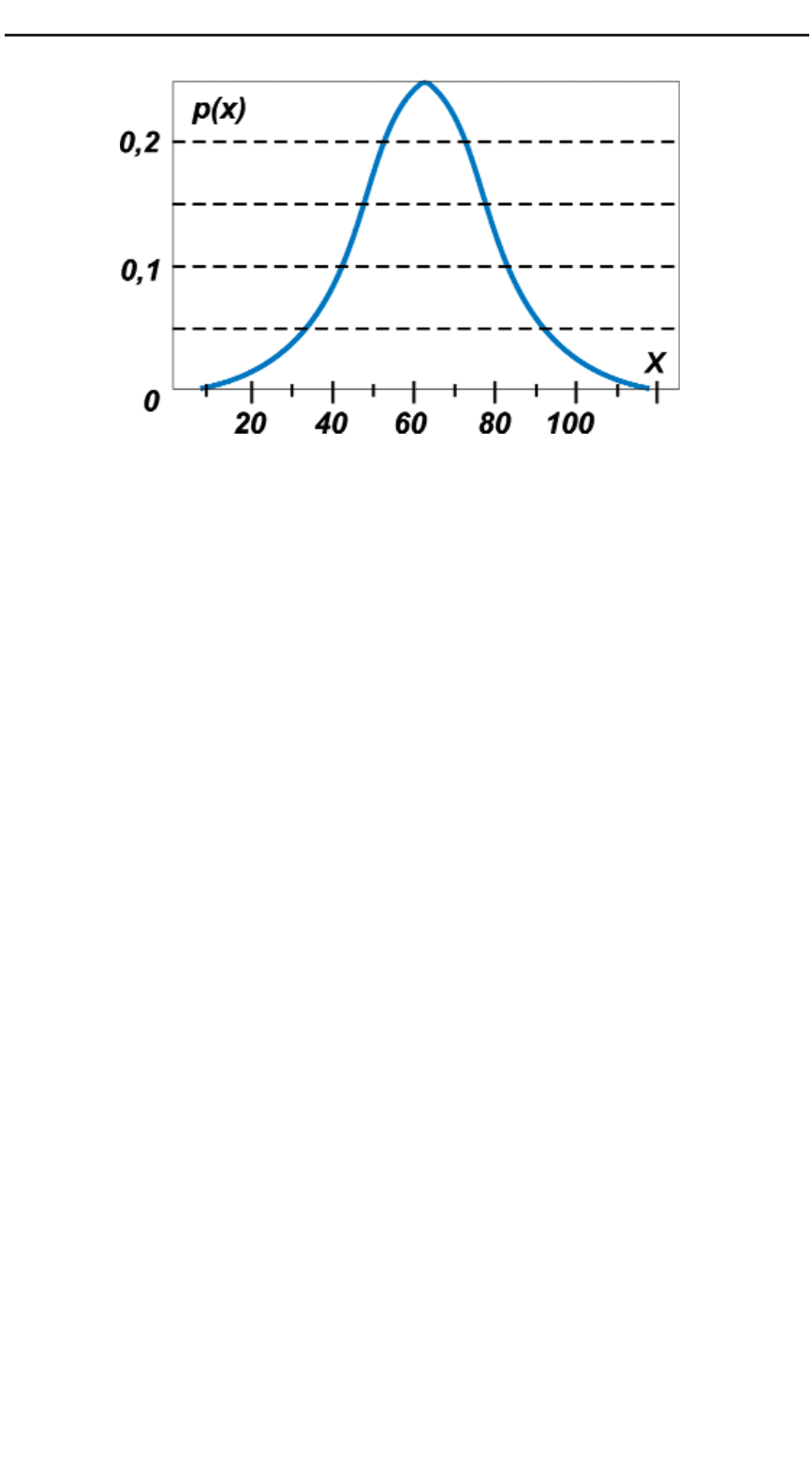
нормальное распределение, или распределение Гаусса. На рисунке

представлен вид функции такого нормального распределения,

а смысл его заключается в том, что в результате большого числа

испытаний относительная частота появления какогото собы

тия группируется вокруг некоторого среднего числа, которое и

можно принять за значение статистической вероятности.

НАНОТЕХНОЛОГИИ ДЛЯ ВСЕХ

www.nanonewsnet.ru

ГЛАВА 2. Законы квантового мира

Рис 39. График функции плотности вероятности при нормальном распределении

Следующий пример наглядно иллюстрирует данный закон

распределения: предположим, мы высыпаем мешок гороха на

пол, держа его в одном и том же вертикальном положении. В

принципе, после этого существуют некоторая вероятность об

наружить горошину в любом месте комнаты, даже в самом

дальнем углу. Однако вероятность того, что мы найдем гороши

ну в самом центре образовавшейся на полу “кучки”, гораздо

выше. Значение вероятности, соответствующее координате

центра кучки, мы и принимаем за статистическую вероятность.

Другой пример: пусть производится серия выстрелов по це

ли. Если учесть, что стрелки палят не наобум, а прилагают все

усилия, чтобы попасть в “яблочко”, то вероятность попадания

пули будет возрастать с приближением к центру мишени.

Но “вернемся к нашим баранам”. Итак, мы решаем задачу

нахождения микрочастицы в некотором объеме dV, например,

ищем местоположение электрона в атоме. Как мы уже знаем, из

за несовершенства измерительных приборов мы не можем точно

указать его местоположение, а можем лишь указать вероятность

dP его местонахождения в той или иной части объема dV.

Кроме того, мы знаем, что эта вероятность dP прямо про

порциональна dV и связана с ней следующим соотношением:

dP=|

·dV

где|Y|

– это квадрат амплитуды волновой функции, мате

матический смысл которой соответствует как раз функции

плотности распределения вероятностей.

Перепишем данное уравнение в виде:

Теперь ясно видно, что |Y|

определяет вероятность нахож

дения частицы в некоторый момент времени t в некотором объ

еме dV, то есть фактически место ее нахождения в точке с коор

динатами x,y,z (объем имеет три измерения)

В атоме водорода единственный электрон как бы образует

вокруг ядра электронное облако – облако отрицательного заряда,

плотность которого в некоторой точке характеризует вероятность

нахождения там электрона. На рисунке показана вероятность об

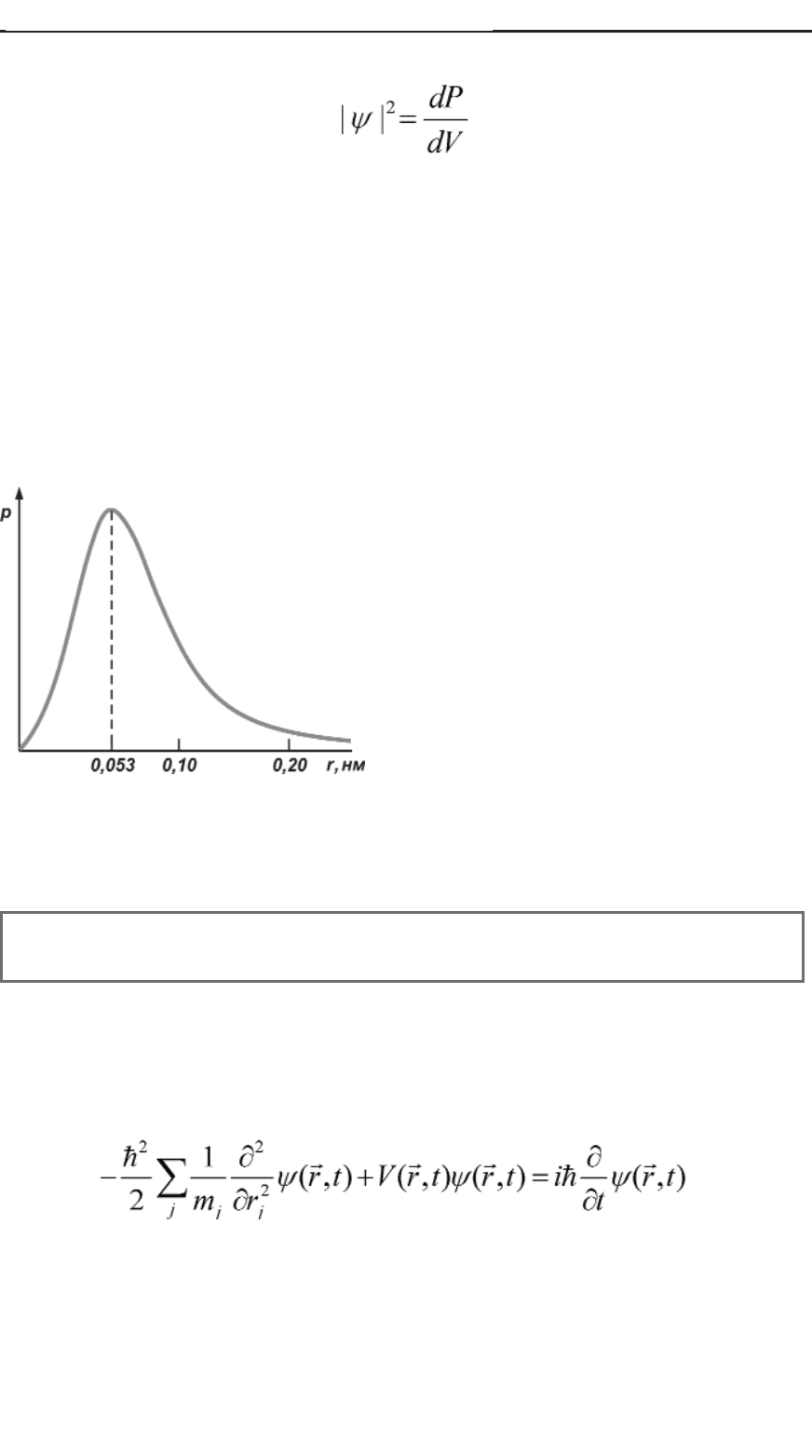
наружить электрон на расстоянии r от ядра атома водорода.

Максимальная вероятность

найти электрон соответствует рас

стоянию r=0,053нм. Вполне воз

можно, что в некоторый момент

электрон находится или ближе к

ядру, или дальше, но вероятность

его обнаружения при этом убывает.

Область пространства, для ко

торой вероятность обнаружения

электрона составляет 95%, назы

вается

ааттооммнноойй ооррббииттааллььюю

Итак, мы усвоили еще одну важную особенность квантовой

механики:

Чтобы определить волновую функцию частицы для конкретной

задачи, физики решают уравнение Шредингера, которое учитывает

влияние электромагнитных сил на ее движение. Это дифференци

альное уравнение в частных производных второго порядка.

Страшно? Для решения этого уравнения потребутся зна

ния, которые не может обеспечить школьная программа по ма

тематике, поэтому мы не будем обсуждать его в нашем курсе. За

метим лишь то, что для квантового мира уравнение Шредингера

играет ту же роль, что законы Ньютона для мира классического.

НАНОТЕХНОЛОГИИ ДЛЯ ВСЕХ

Поведение элементарных частиц носит вероятностный

характер, описываемый волновой функцией

Рис 40. График вероятности обнаружения

электрона на разном расстоянии от ядра

www.nanonewsnet.ru

ГЛАВА 2. Законы квантового мира

Уравнение Шредингера и Периодическая сис

тема элементов Менделеева

Многообразие нашего мира объясняется огромным разно

образием элементов, существующих во Вселенной. В настоя

щее время науке известно более 110 элементов с уникальными

физикохимическими свойствами.

Мы знаем, что атом любого вещества состоит из положи

тельно заряженного ядра, окруженного облаком электронов.

Ядро, в свою очередь, состоит из некоторого количества прото

нов, заряженных положительно, и нейтронов, не имеющих ни

какого заряда. Атомы стабильны потому, что в своем основном

состоянии они энергетически нейтральны, то есть положитель

ный заряд ядра полностью скомпенсирован суммарным заря

дом электронов (число протонов в ядре атома равно числу

электронов на его орбиталях).

Ученые всегда стремились упорядочить все разнообразные

элементы в некую единую логическую схему. Самой удачной

попыткой сделать это оказался принцип, предложенный в 1869

году русским ученым Д.И. Менделеевым, который лег в основу

современной Периодической системы элементов.

В таблице Менделеева элементы расположены в порядке

возрастания их

ааттооммнныыхх ннооммеерроовв

(числа протонов в ядре). Нап

ример, атомный номер водорода равен единице. Это говорит о

том, что ядро атома водорода состоит из одного протона, вокруг

которого вращается единственный электрон.

Элементы распределены по горизонтальным рядам, назы

ваемым

ппееррииооддааммии,,

и вертикальным столбцам, называемым

ггррууппппааммии

. Такое распределение основывается на некоторой

общности физикохимических свойств элементов, которые пе

риодически изменяются в соответствии с их атомным номером.

Например, все элементы первой группы (кроме водорода) яв

ляются щелочными металлами, а все элементы восьмой группы

представляют собой благородные газы.

Все это здорово, но при чем же здесь уравнение Шрединге

ра? Мы помним, что согласно принципу Паули, электронная

оболочка атома не может одновременно содержать два электро

на в одном и том же состоянии. А поскольку число электронов

в некоторых атомах достигает десятков и даже сотен, то возни

кает естественный вопрос: как же они все там расположены?

100

НАНОТЕХНОЛОГИИ ДЛЯ ВСЕХ

Рис 42. Форма s*, p* и d* орбиталей

Решение волнового уравнения Шредингера позволило вы

числить четыре параметра, которых достаточно, чтобы пол

ностью охарактеризовать состояние любого отдельно взятого

электрона. Эти параметры получили название “четыре квантовых

числа”. Полученная квантовая четверка – своего рода “паспорт”,

однозначно идентифицирующий каждый электрон в атоме.

Чем больше число

, тем дальше элект

рон отстоит от ядра и тем выше его энергия.

Выделяют четыре энергетических оболочки:

KK((nn==11)),, LL((nn==22)),, MM((nn==33))

NN((nn==44))..

Но одного деления на оболочки для пол

ного описания состояния электрона недоста

точно. Дело в том, что каждая энергетическая

оболочка атома может “вмещать в себя” раз

ное количество электронов. Понятно, что для

того, чтобы обеспечить их уникальность (согласно принципу

Паули), каждая оболочка должна разбиваться еще на несколько

подоболочек, получивших название орбиталей.

Решение уравнения Шредингера позволило вычислить

формы всех существующих видов электронных орбиталей. Их

всего четыре: s*, p*, d* и fорбитали. На рисунке изображен вид

s, p и dорбиталей. Sорбиталь имеет сферическую форму, p

орбиталь – форму гантелей, dорбиталь похожа на трехмерный

четырехлепестковый цветок.

ГГллааввннооее ккввааннттооввооее ччииссллоо

(число

) характеризует оболочку, в

которой находится электрон. Оно соответствует повыша

ющимся энергетическим уровням оболочек.

Рис 41. Схема атома с

двумя энергетическими

оболочками

ООррббииттааллььннооее ккввааннттооввооее ччииссллоо

(число

) определяет форму

электронных орбиталей.

101

www.nanonewsnet.ru

ГЛАВА 2. Законы квантового мира

Каждому типу орбитали соответствует определенная энер

гия электрона. При переходе с одной орбитали на другую элект

рон испускает излучение, характерное для соответствующего

типа линий в атомном спектре, откуда, собственно, и произош

ло их название:

sорбиталь соответствует “резкой” (sharp) sлинии атомно

го спектра;

pорбиталь соответствует “главной” (principal) pлинии;

dорбиталь соответствует “диффузной” (diffuse) dлинии;

fорбиталь соответствует “фундаментальной” (fundamental)

f*линии;

Энергетические уровни оболочек содержат в себе разное

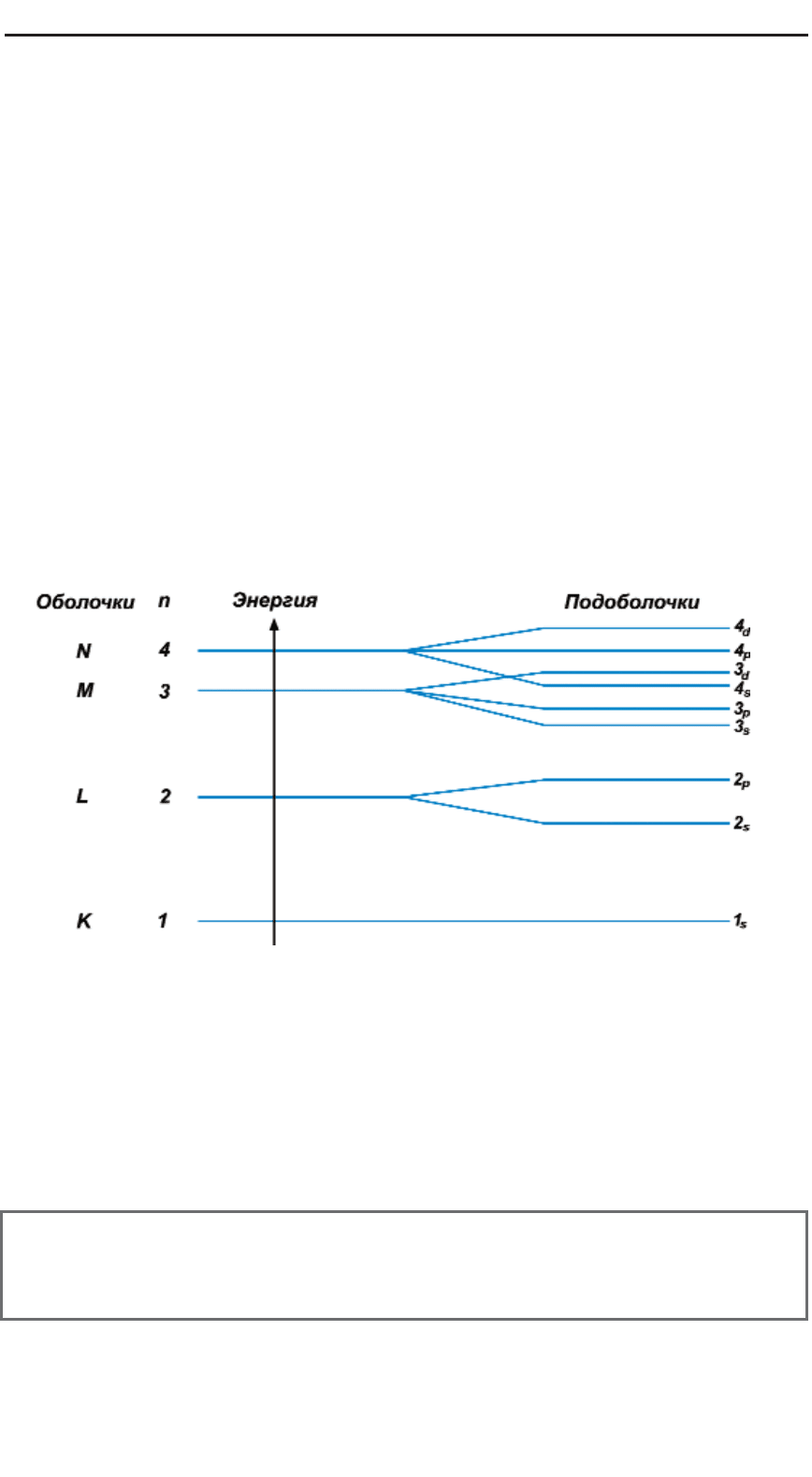
количество орбиталей. На рисунке показано относительное

расположение энергетических уровней орбиталей, принадле

жащих первым четырем электронным оболочкам:

Рис 43. Порядок расположения атомных орбиталей и оболочек

Так, первая Коболочка содержит только одну s*орбиталь.

Следовательно, на первом энергетическом уровне может

“жить” либо один, либо два электрона. Вторая оболочка вклю

чает не только s*, но и 3 p*орбитали. Здесь обитают уже 2+6=8

электронов и т.д. Обратите внимание на особенность 4sподобо

лочки: ее энергетический уровень расположен чуть ниже 3dпо

доболочки.

Электрон – это не только отрицательно заряженная части

ца, но еще и миниатюрный магнит, подобный стрелке компаса

ММааггннииттннооее ккввааннттооввооее ччииссллоо

(число

) отражает влияние

внешнего магнитного поля на состояние электрона и

определяет ориентацию орбиталей в пространстве

102

НАНОТЕХНОЛОГИИ ДЛЯ ВСЕХ

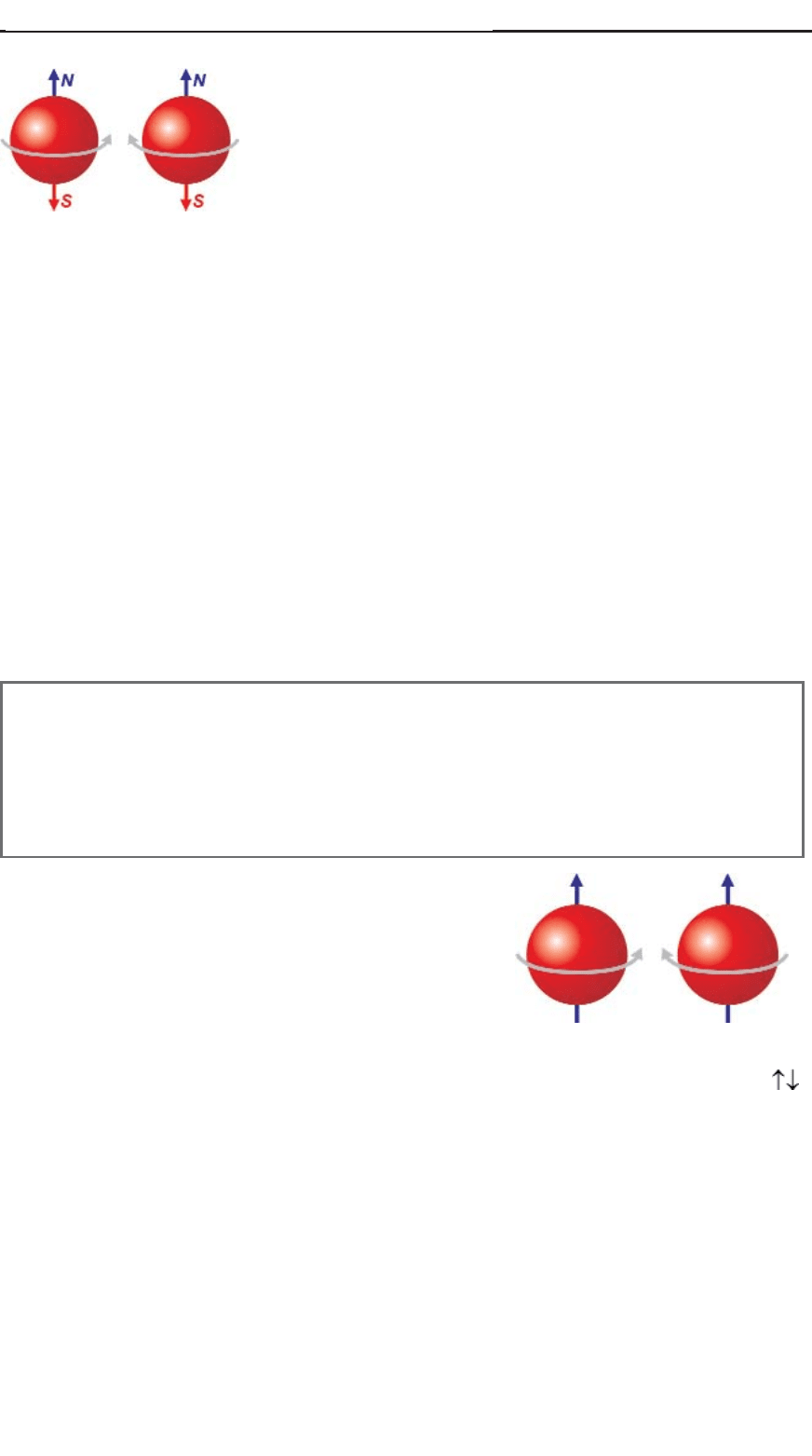
ССппииннооввооее ккввааннттооввооее ччииссллоо

(число

), показывает направление

собственного момента вращения, который называется спином

(от англ. “spin” – вращаться). Вращаться электрон может

только в двух состояниях: по часовой стрелке, “спин вверх”

(s=+1/2), и против часовой стрелки, “спин вниз” (s=–1/2).

с северным и южным полюсами. Электрон

нельзя размагнитить, но зато можно повора

чивать в пространстве, воздействуя на него

внешним электромагнитным полем.

Число

также показывает максимально

возможное число орбиталей для каждой

оболочки l.

Всего на оболочке может быть:

· одна s–орбиталь;

· три p–орбитали;

· пять d– орбиталей;

· семь f– орбиталей.

Давайте теперь пристальнее посмотрим на один отдельно

взятый электрон. Он, подобно планете Солнечной системы,

вращается не только вокруг положительно заряженного ядра,

но и вокруг собственной оси. Поэтому одной из важнейших ха

рактеристик при описании электрона является его спиновое

квантовое число.

Итак, принимая во внимание при

веденные выше сведения, принцип

запрета Паули можно переписать сле

дующим образом:

Никакие два электрона в атоме не

могут иметь одинаковые наборы четы*

рех квантовых чисел.

ЭЭллееккттррооннннааяя ккооннффииггуурраацциияя ээллееммееннттаа

 это запись распреде

ления электронов в атоме по оболочкам и орбиталям. Она

обычно записывается для атомов в основном состоянии соглас

но следующим правилам:

1. Электроны заполняют орбитали последовательно, от

меньшего энергетического уровня к большему. Низшие по

энергии орбитали всегда заполняются первыми.

Рис 44. Магнитные полюсы

электрона

Рис 50. Спин электрона. Пару

электронов с противоположными

спинами изображают cтрелками