Рухин Л.Б. Основы литологии. Учение об осадочных породах
Подождите немного. Документ загружается.


588
ФАЦИИ
И
МЕТОДЫ
ФАЦИАЛЬНОГО
АНАЛИЗА
Среди
статистических
характеристик
наиболее
важны
средnие
велu
чunы.
К
ним
относят
среднее
арифметическое,
медиану,
моду,
среднее
геометрическое
и
некоторые
другие
величины,
представляющие
собой
как
бы
центры,
вокруг
которых
группируется
большая
часть
наблюдаемых
значений
аргументов.
Из
всех
средних
наиболее
важно
средneе
арuфм,еmuчеСYi,ое
Ма,
оно
чаще
всего
используется
при
теоретич
еCI\ИХ
и
практических
исследо
ваниях.
В
математической
статистике
доказывается,
что
сумма
отклонений
величин,
входящих
в
данную
совокупность,
от
их
среднего
арифметиче
ского,
равна
нулю.
Кроме
того,
сумма
квадратов
отклонений
значений
данных
величин
от
их
среднего
арифметического
меньше
суммы
квадратов
ОТIшонений
от
любой
другой
величины.
Для
того
чтобы
определить
среднюю
арифметическую
М
а
для
каких
либо
величин
Х,
Х2,
...
,
Х
n
,
входящих
В
данную
СОВОI<УПНОСТЬ,
необходимо
сумму
этих
величин
разделить
на
их
число
М
а
=
Х
1
+
Х
2
+
..
. +
Х
n
= '
~
Х
•
п
·
11.
Например,
среднее
арифметичеСlюе
поперечНlШОВ
гальки,
составляю
щих
24, 18
и
15
см"
будет
равно
Ма
= 24+1:+15 = 19
см,.
в
тех
случаях,
когда
I{аждый
член
данной
совокупности
встречается
в
ней
несколько
раз,
среднее
арифметичеСlюе,
Лвляющееся
в
данном
слу
чае
взвешеnnым,
средnим,
арuфм,еmuчесYi,Uм"
определяется
по
формуле
М
а
=
nlx
1
+
П
2
Х
2
+
...
+
nтХ
m
=
~
пх
,
n
1
+
11.2
+ ...
n
т
'
2:
11.
г
де
Х
1
,
Х
2
,
.•
. ,
Хт
-
члены
данной
совокупности;
n
1
,
n
2
••
.
nт
-
частоты
их
нахождения.
Предположим,
что
нужно
вычислить
среднюю
Оl<ругленность
сово
RУПНОСТИ
галек,
обладающих
округленностью
1, 2, 3, 4
и
5
баллов;
коли
чество
галек
в
каждой
и
з
этих
групп
было
определено
предварительным
подсчетом.
Вычисления
располагаются
в
виде
следующей
схемы
(табл.
12-XIV).
Табл,uца
12-XIV
Схема
вычисления
среднего
а,рифметичеСIЮГО
Баллы
окатанности
(Х)
1
2
3
4
5
Количество
галек
с
данным
баллом
ок
руг ленности
(11.)
10
35
17
5
3
1:
n = 70
166
lII
a
= - - = 2,1
70
ПХ
10
70
51
20
15
1:
nх
= 166

НАМ
ЕРАЛЬНЫЕ
МЕТОДЫ
ФАЦИА
J
IЬН
ОГО
АНАЛИЗА
589
в
тех
случанх,
когда
значенин
величин,
вх;однщих
в
данную
совокуп
но
с
ть,
и
их
частоты
выражены
многозначными
цифрами,
вычисление
сродней
взв-ешенной
по
приведенной
схеме
становитсн
утомительным
и
подвержено
ошибкам.
В
этих
случанх
пользуютсн
'
так
называемым
сокра
щенным
способом
вычисленин
и:
рассчитывают
среднюю
взвешенную,
исходя
на
равенства
~n
(
х-а)
2"n
Ма
=
а
+
ЧИС
J
IO
а
выбираетсн
с
таюш
расчетом,
чтобы
разность
х
-
а
была
130
а
МОiJШО
проще
и
меньш
е
.
Это
бывает
в
том
случае,
если
а
приблизи
тельно
равно
среднему
арифметическому,
оцениваемому
на
глаз
при
помощи
просто
го
обозрения
данной
совон:упности.
Второй
чл
ен
правой
части
равенства
-
сумма
произведений
отклоне
ний
от
условной
средней
на
ча
с
тоту
соответствующих
классов,
деленная
на
общее
количество
наблюдений
-
на
з
ывается
первым
моментом
отно
сительно
условной
среднеЙ*
.
Он
представлнет
собой
как
бы
ту
поправку,
которую
нужно
прибавить
Н_
условной
средней,
чтобы
получить
истинное
среднее
арифметическое.
,
Этот
способ
вычисленин
особенно
часто
применнетсн
при
обработке
данных
гранулом
е
тричеСI{ОГО
анализа
(см.
§ 65).
Если
обозначить
величину
первого
момента
относительно
условной
средней
через
Vl'
то
среднее
арифметическое
буд
е т
равно
Л1
а
=
а
+ V
1
.
Определим
по
этому
способу
среднее
арифметическое
округленности
гален,
охарактеризованных
табл.
13-XIV.
Таблuца
13-XIV
Схема
вычисления
среднего
арифметического
по
сокращенному
способу
Баллы
округ
ле
н
ности
(х)
1
2
3
4
5
Н:оличество
галек
с
данным
балом
округленности
(n)
10
35
17
5
3
26
111
а
= 2 +
70
= 2,4
х-а
(
а
=
2)
-1
О
+1
+2
+3
n
(х
-
а)
-10
О
+17
+10
+9
1:
- =
10
1:
+ = 36
1:
= +
26
Пос
ле
среднего
арифметического
наиболее
важной
средней
величи
ной
нвляется
медиана
Md.
Если
отдельные
значенин
изучаемого
признак
а
расположить
в
рнд
в
порндк
е
их
возрастанин
или
убыванин,
то
величина
*
Моменты,
вычис
л
я
емые
н
а
основании
определения
отклонений
от
средней
арифметической,
называются
центра
J
IЫ
-
!Ы
МИ.
Первый
ц
ен
трал
ьны
й
момент
всегда
ра
lJ
e H
нулю.
Ред.
590
ФАЦИИИ
МЕТОДЫ
ФАЦИАЛЬНОГО
АНАЛИЭА
при
знюш,
соот:цетствующая
среднему
члену
ряда,
или
полусумма
двух
средних
членов
и
будет
медианой.
Иначе
говоря,
мер;иана
делит
совокуп
ность
на
две
равны
е
части.
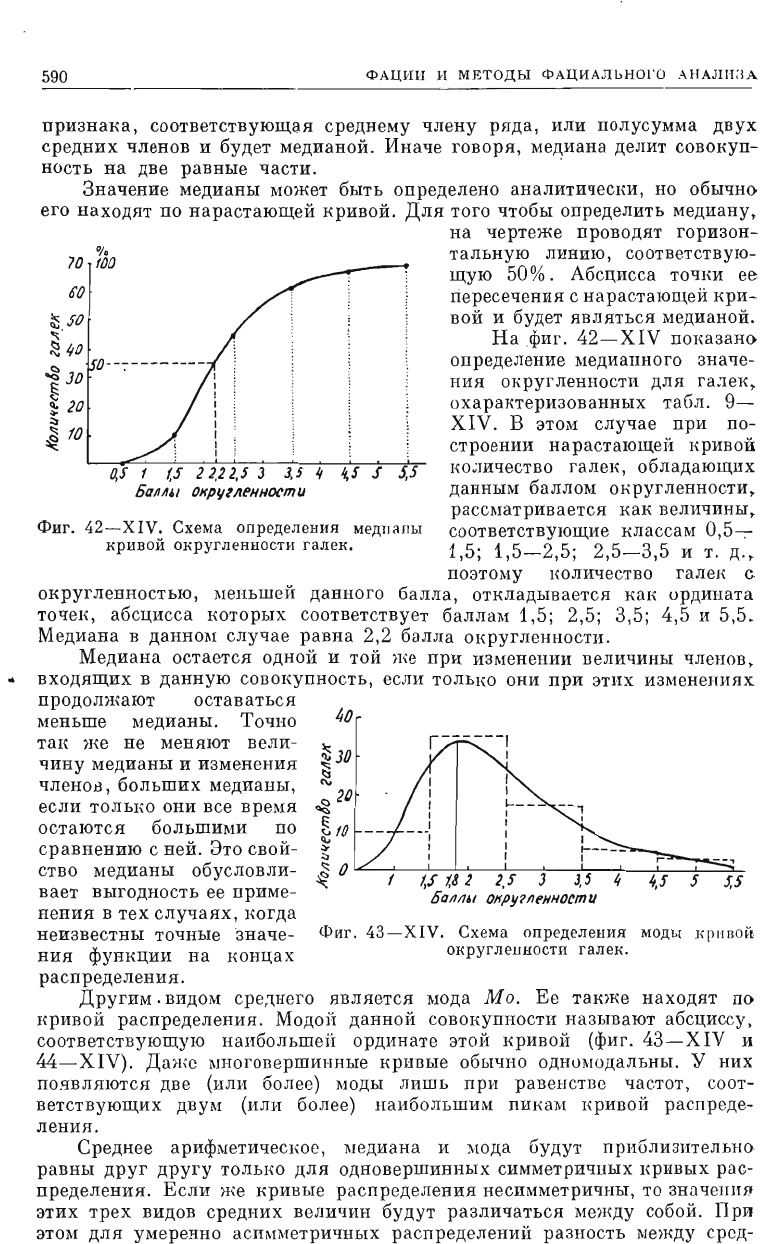
Значение
медианы
может
быть
определено
аналитичеСIШ,
но
обычн(}
его
находят
по
нарастающей
кривой.
Для
того
чтобы
определить
медиану,
на
чертеже
проводят
горизон-
%
70
100
сО
o,.f
f
f,S
г
2,2
J,s
3
3.5
Балл"
ОКРlJlЛt'нн(}{'mu
Фиг.
42-XIV.
Схема
определения
медпariы
КРИВОЙ
округленности
галек.
тальную
линию,
соответствую
щую
50%.
Абсцисса
ТОЧIШ
ее
пересечения
с
нарастающей
кри
вой
и
будет
являться
медианой.
На
фиг.
42-XIV
показан(}
определение
медианного
значе
ния
Оl{ругленности
для
галек,
охарю\теризованных
табл.
9-
XIV.
В
этом
случае
при
по
строении
нарастающей
I{РИВОЙ
!{оличество
галек,
обладающих
данным
баллом
Оl\ругленности,
рассматривается
как
величины,
соотве
т
с
твующи
е
классам
0,5-;-
1,5;
1,5-2,5;
2,5-3,5
и
т.
д.,
поэтому
ноличество
галек
с.
онругленностью,
меньшей
данного
балла,
отнладывается
l\al{
ордината
точ
еl{,
абсцисса
ноторых
соответствует
баллам
1,5; 2,5; 3,5; 4,5
и
5,5.
Медиана
в
данном
случае
равна
2,2
балла
Оl{ругленности.
Меди
ана
остается
одной
и
той
же
при
изменении
величины
членов,
входящих
в
данную
совокупнос
ть
,
если
толы
{о
они
при
этих
изменениях
продолжают
оставаться
меньше
медианы.
Точно
40
таи
же
не
меняют
вели-
чину
медианы
и
изменения
члеНОlJ,
больших
медианы,
если
только
они
все
время
остаются
большими
по
сравнению
с
ней.
Это
свой
ство
медианы
обусловли
вает
выгодность
ее
приме
нения
в
тех
случаях,
когда
неизвестны
точные
значе
ния
функции
на
концах
распределения.
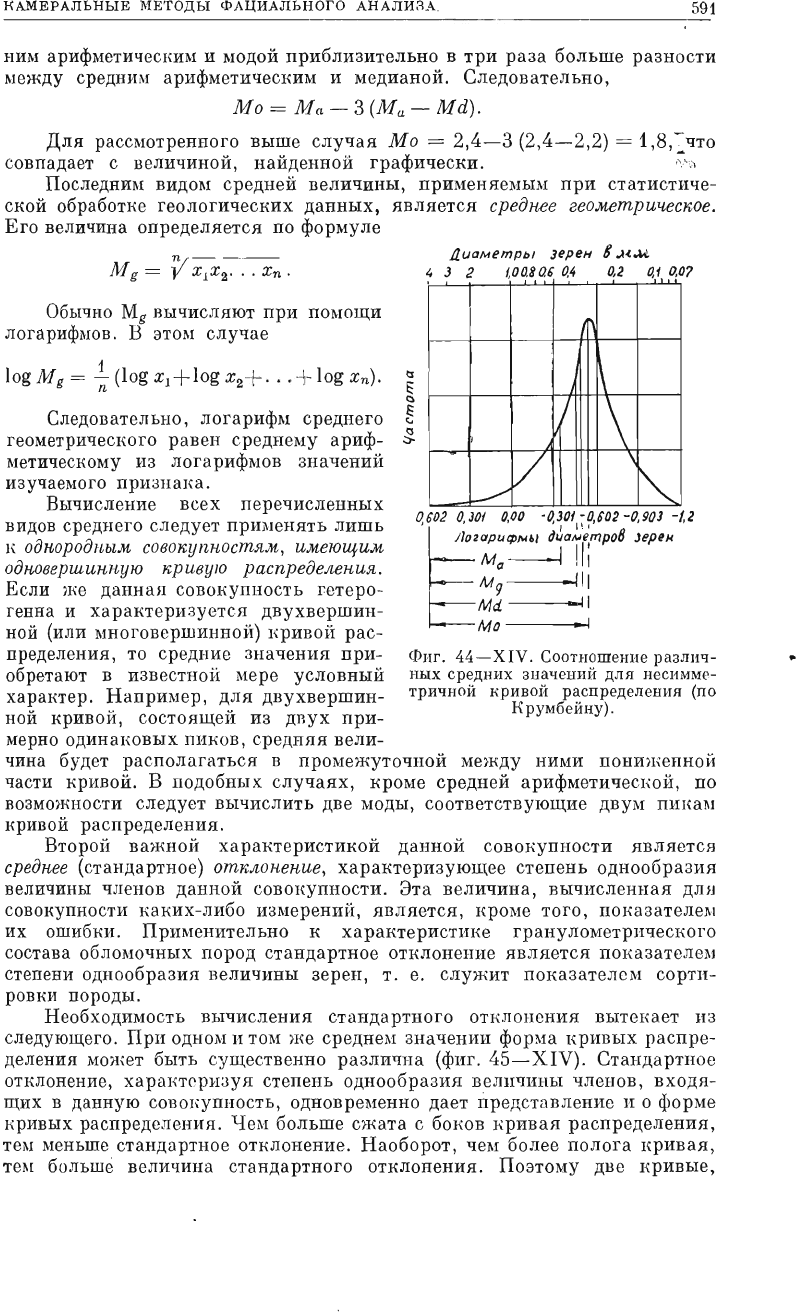
Фиг.
43-XIV.
Схема
определения
моды
J(РНI30Й
округленности
галек.
Другим
.
видом
среднего
является
мода
М
о.
Ее
так
же
находят
п(}
нривой
распределения.
Модой
данной
совонупности
называют
абсциссу,
соответствующую
наибольшей
ординате
этой
НРИВОЙ
(фиг.
43-XIV
.
и
44-XIV).
Даже
многовершинные
нривые
обычно
одномодальны.
У
них
появляются
две
(или
более)
моды
лишь
при
равенстве
частот,
соот
ветствующих
двум
(или
более)
наибольшим
пинам
I{РИВОЙ
распреде
ления.
Среднее
арифметичесное,
м
е
диана
и
мода
будут
приблизителыю
равны
друг
другу
тольно
для
одновершинных
симметричных
нривых
рас
пред
еления.
Если
же
иривые
распределения
несимметричны,
то
значения
этих трех
видов
средних
величин
будут
различаться
между
собой.
При
этом
для
умеренно
аСИJlIметричных
распределений
разность
между
срсд-
НАМЕРАЛЬНЫЕ
МЕТОДЫ
ФАЦИАЛЬНОГО
АНАЛИ:=lА
591
ним
арифметическим
и
модой
приблизительно
в
три
раза
больше
разности
между
средним
арифметичесним
и
медианой.
Следовательно,
Мо
=
Ма-3(Мu.-
Md).
Для
рассмотренного
выше
случая
Мо
=
2,4-3
(2,4-2,2)
=
1,8,
""
что
совпадае
т
с
величиной,
найденной
графичесни.
;:
'с;
Последним
видом
средней
величины,
применяемым
при
статистиче
ской
обработке
геологичесних
данных,
является
среднее
геометрическое.
Его
величина
определяется по
формуле
Обычно
M
g
вычисляют
при
помощи
логарифмов.
В
этом
случае
1
log M
g
= - (log
x1+log
Х
2
+ ... -I-log
х
n
).
n
Следовательно,
логарифм
среднего
геометрического
равен
среднему
ариф
метическому
И3
логарифмов
значений
и
з
учаемого
признюй.
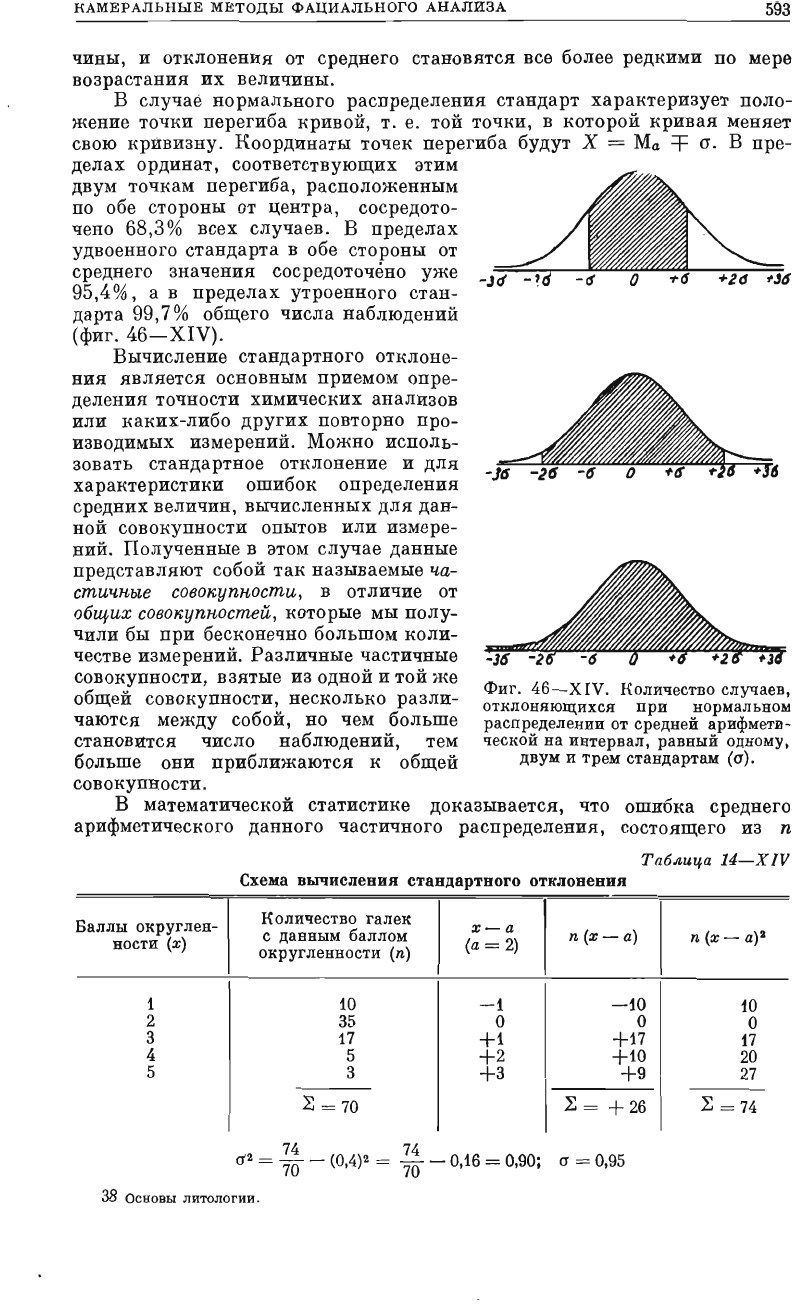
Вычисление
всех
перечисленных
видов
среднего
следует
применять
лишь
к
однородnым
совокуnnостям,
имеющим
одновершинnую
кривую
распределения.
Если
же
даннан
СОВОI\УПНОСТЬ
гетеро
генна
и
харю{теризуется
двухвершин
ной
(или
многовершинной)
нривой
рас
пределения,
то
средние
значения
при
обретают
в
изв
ес
тной
мере
условный
харантер.
Например,
для
двухвершин
ной
I\РИВОЙ,
состоящей
И3
двух
при
мерно
одинаl\ОВЫХ
ПИI\ОВ,
средняя
вели-
Диаметры
зерен
G
.Н""-
4 J
г
/008
а6
0."
~2
41
о,о?
, '
\
/
\
!
~
V
~
0,60.2
O,Jo./
0.0.0.
-о,~0.11~f,оО2
-0.,903
-t,Z
l=
IOг
аРЩР",·1
dllаЛJеmро8
зерен
Mo~!"
- M
g
.111
~Mc!
~I
I---
Mo
....
1
Фиг.
44-XIV.
Соотношение
различ
ных
средних
значений
ДJIЯ
несимме
тричной
кривой
распределения
(по
КрумбеЙну).
чина
будет
располагаться
в
промежуточной
между
ними
пониженной
части
I\РИВОЙ.
В
подобных
случаях,
l\роме
средней
арифметичеСI{QЙ,
по
возможности
следует
вычислить
две
моды,
соответствующие
двум
ПИIШМ
I\РИВОЙ
распределения.
Второй
важной
хараl\теРИСТИI\ОЙ
данной
СОВОI\УПНОСТИ
является
средnее
(стандартное)
отклоnеnие,
хараl\теризующее
степень
однообразия
величины
членов
данной
совонупности
.
Эта
величина,
вычисленная
для
СОВОI\УПНОСТИ
наI\их-либо
и
з
мерений,
является,
l{pOMe
того,
ПОI{азателем
их
ошибю[.
Применительно
1\
характеристике
гранулометрического
состава
обломочных
пород
стандартное
ОТI\лонение
является
ПOIйзателем
степени
однообразия
величины
зерен,
т.
е.
служит
ПОI\азателом
сорти
роВl{И
породы
.
Необходимость
вычисления
стандартного
ОТl\лонения
выты{ает
из
следующего
.
При
одном
и том
же
среднем
значении
фор~ш
I\РИВЫХ
распре
деления
может
быть
существенно
различна
(фиг.
45-XIV)
.
Стандартное
ОТIшонение,
хараl\теризуя
степень
однообразия
величины
членов,
входя
щих
в
данную
СОВО
I
{УШIОСТЬ,
одновременно
дает
пред
ставл
ение
и
о
форме
нривых
распределения.
Чем
больше
сжата
с
БОI{ОВ
I{ривая
распределения,
тем
меньше
стандартное
отклонение.
Наоборот,
чем
более
полога
I\ривая,
тем
больше
величина
стандартного
ОТl\лонения.
Поэтому
две
нривые,

592
ФАЦИИ
И
МЕТОДЫ
ФАЦИАЛЬНОГО
АНАЛИЗА
изображенные
на
45
-
-XIV,
при
одном
и
том
же
среднем
значении,
харак
теризуются
резко
неодиню{Овым
стандартом
.
При
вычислении
стандартного
отклонения
исходят
из
разностей
величин
(х),
образующих
данную
совокупность,
и
ее
среднего
арифметиче
CI,oro
(М
а
).
Затем
должны
быть
учтены
частоты
(n),
с
которыми
ЭТИ
откло
нения
встречаются
в
данной
совокупности.
Если
взять
просто
сумму
всех
отклонений
от
средней
арифметичеСI{ОЙ,
то
она,
как
уже
ГОВОРИЛОСЬ
выше,
всегда
будет
равна
нулю.
Поэтому
нужно
рассматривать
эти
отнлонения
независимо
от
их
знана,
вводя
в
формулу,
например,
их
l\вадраты.
Тогда
мерилом
степени
однородности
величин
в
данной
СОВОI\УПНОСТИ
будет
являться
сумма
произведений
Iша
Фиг
.
45-XIV
.
Различные
формы
I\РИВЫХ
распределения,
обладающих
одинаковым
.
средним
значением.
дратов
отнлонений
значений
.
от
среднего
арифметичесного
на
их
частоту,
делен
ная
на
общее
ноличество
наблюдений
.
Эта
величина
называется
иначе
вторы.м
-мо-меnто-м
и
обозначается
обычно
через
а2
.
Следовательно
,
~n
(х-М
а
)2
,,2
=
ИЛИ
~n
Последняя
величина
и
называется
стандартным
отнлонением
(стан
дартом)
или
средnи-м
1'ОвадратичеС1'Ои-м
от1'Олоnеnие-м
.
Квадрат
стандартного
отнлонения,
т.
е.
величина
а&
называется
дисперсией.
Стандартное
отнлонение
обычно
вычисляется
по
сонращенному
способу
при
помощи
моментов,
вычисл-енных
относительно
условной
средней,
подобно
тому
I\Ю,
это
делалось
при
определении
среднего
арифме
тичеСI,ОГО
.
В
данном
случае
исходят
из
равенства
~
n
(х
_
а)2
а
2
=
-
~n
-(М
а
-а)2,
где
а
выбирается
с
тю,им
расчетом,
чтобы
разность
х
-
а
была
возмошно
меньше
и
проще.
Эта
формула может
быть
упрощена,
если
воспользоваться
равенством
М
а
=
а
+ V
1
,
а
величину
второго
момента
относительно
условной
сред
ней
обозначить
через
V2.
Тогда
И
J
IИ
Стандартное
от
I{JIO
н
eI-гие
предстаВJlяет
собой
второй
центральный
момент.
Оно
вырашено
всегда
в
единицах
интервала.
Схема
его
вычисле
ния
приводится
нише
на
примере
рассмотренной
выше
СОВОКУПНОСТlI
галеI,
(табл.
14-XIV)
.
ПрантичеСIШ
величины
среднего
размера
и
стандартного
отклонения
рассчитывают
однов
ременно.
-у
тан
называемых
нормальных
распределений,
играющих
очень
большую
роль
в
теории
вероятностей
и
в
ее
приложениях,
среднее
арифм
е
тическое
совпадает
с
модой
и
медианой.
-у
них
среднее
значение
предста
вляет
собой
наиболее
вероятное
значение
данной
статистичеСI,ОЙ
вели-
ИАМЕРАЛЬНЫЕ
МЕТОДЫ
ФАЦИАЛЬНОГО
АНАЛИЗА
593
чины,
и
отилонения
от
среднего
становятСя
все
более
редиими
по мере
возрастания
их
величины.
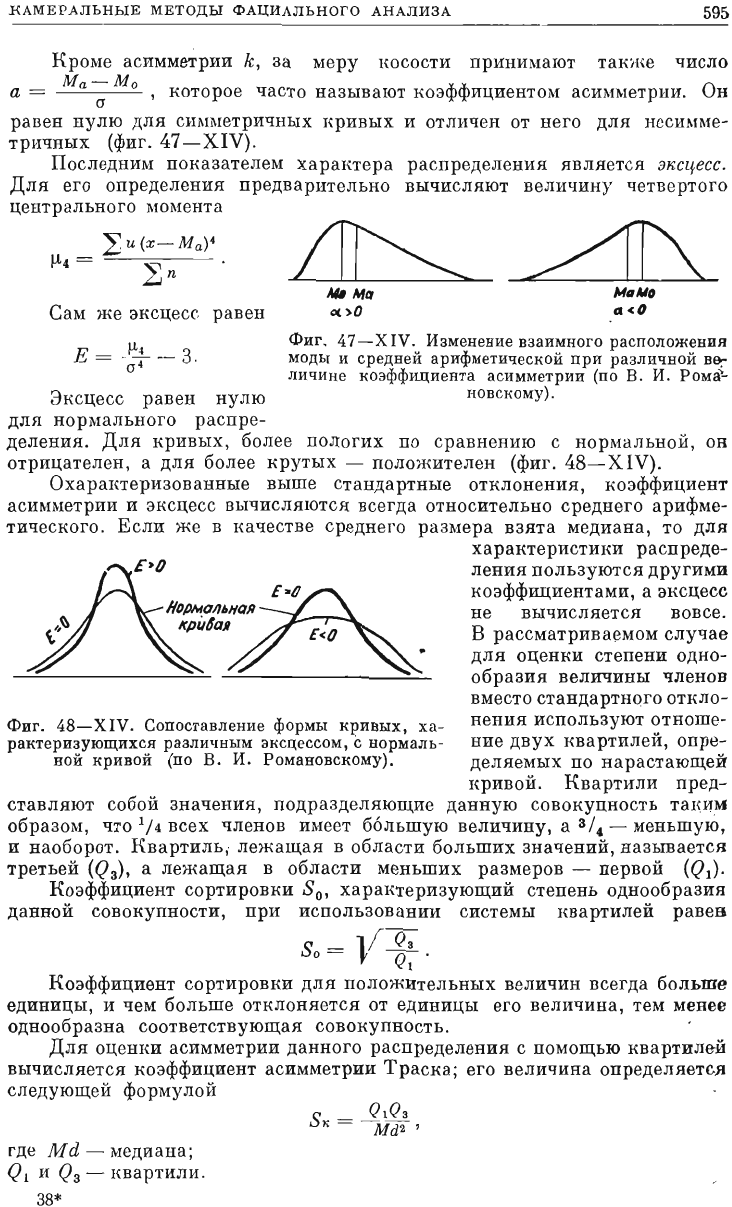
В
случае
нормального
распределения
стандарт
хараитеризует
поло
жение
точни
перегиба
нривой,
т.
е.
той
точни,
в
ноторой
нривая
меняет
свою
нрИвизну
.
:Координаты
точен
перегиба
будут
Х =
М
а
=f
а.
В
пре
делах
ординат,
соответствующих
этим
двум
точнам
перегиба,
расположенным
по
обе
стороны
от
центра,
сосредото
чено
68,3%
всех
случаев.
В
пределах
удвоенного
стандарта
в
обе
стороны
от
среднего
значения
сосредоточено
уже
95,4%,
а
в
пределах
утроенного
стан
дарта
99,7%
общего
числа
наблюдений
(фиг.
46-XIV).
Вычисление
стандартного
отнлоне
ния
является
основным
приемом
опре
деления
точности
химичесних
анализов
или
наних-либо
других
повторно
про
изводимых
измерений.
Можно
исполь
зовать
стандартное
отнлонение
и
для
хараитеристиии
ошибои
определения
средних
величин,
вычисленных
для
дан-
ной
совоиупности
опытов
или
измере-
ний.
Полученные
в
этом
случае
данные
представляют
собой
таи
называемые
ча
сmичnые
coeo/'i,ynnocmu,
в
отличие
от
общих
coeo/'i,ynnocmeu,
иоторые
мы
полу
чили
бы
при
бесионечно
большом
иоли
честве
измерений.
Различные
частичные
совоиупности,
взятые
из
одной
и
той
же
общей
совоиупности,
несиольио
разли
чаются
между
собой,
но
чем
больше
становIiтСЯ
число
наблюдений,
тем
больше
они
приближаются
и
общей
совоиупности.
Фиг.
46-XIV.
Количество
случаев,
отклоняющихся
при
нормальном
распределении
от
средней
арифмети
ческой
на
интервал,
равный
одному,
двум
и
трем
стандартам
(<1).
В
математичесиой
статистике
доиазывается,
что
ошибиа
среднего
арифметического
данного
частичного
распределения,
состоящего
из
n
Таблица
14-Х
/V
Схема
вычисления
стандартного
отклонения
Баллы
округлен-
Количество
галек
с
данным
баллом
х-а
n
(х-
а)
n
(х-
а)2
ности
(х)
округленности
(n)
(а
=
2)
1
10
I
-1
-10
10
2
35
О
О
О
3
17
+1
+17
17
4
5
+2
+10
20
5
3
+3 +9
I
27
1:
=
70
I
1:
=
+26
1:
=
74
0'2
=
~~
-
(0,4)2
=
~~
- 0,16 = 0,90;
<1
= 0,95
38
ОСНОВЫ
ЛИТОЛОГИИ
.

594
ФАЦИИ
И
МЕТОДЫ
ФАЦИАЛЬНОГО
АНАЛИЗА
наблюдений,
равна
отношению
стандартного
отклонения
к
корню
квадрат
ному
из
числа
наблюдений,
т.
е.
а
а
т
=
Уn
.
Отношение
этой
величины
к
самому
среднему
арифметическому
М
а
,
выраженному
в
процентах,
принимается
за
показатель
точности
ис
следования
р
=
100а
т
%.
М
а
Ошибка
стандартного
отклонения
равна
а
G --- - --
(]
- J/ 2n
или
а(]
= 0,707
а
т
·
Дисперсии
или
стандартные
отклонения
величин
различных
размер
ностей
нельзя
сравнивать
друг
с
другом,
так
как
они
выражены
в
неоди
ню\Овых
единицах.
Например,
нельзя
сравнивать
между
собой
стандарт
ные
отклонения
размера
галек
и
их
округленности.
Однако
в
ряде
случаев
необходимо
обладать
сравнимыми
мерами
рассеяния.
Такой
мерой
являет
ся
коэффициент
изменчивости
V,
равный
отношению
стандартного
откл
о
нения
к
среднему
арифметическому.
Его
выражают
в
процентах,
умножая
для
этого
на
100
v =
100~
%.
М
а
После
определения
этой I!еличины
показатель
точности
исследования
вычисляется
по
формуле
v
р
=
уn
'
где
n -
число
измерений.
Чем
точнее
произведено
исследование,
тем
меньше
величина
Р.
При
детальны:х,
исследованиях,
кроме
среднего
арифметического
и
среднего
отклонения,
вычисляют
еще
два
показателя,
характеризующих
форму
кривой
распределения.
Одним
из
них
является
ее
асимметрия,
т.
е.
неодинаковое
размещение
значений
по ту
и
другую
сторону
от
сред
него
арифметичеСI\ОГО:
Для
измерения
асимметрии
служит
величина
третьего
центрального
момента
f.L3,
вычисляемая
подобно
стандартному
отклонению:
Если
совокупность
симметрична,
-
то
данная
величина
превратится
в
-нуль
.
-
Если
же
кривая
распределения
несимметрична,
то
величина
f.Ls
будет
больше
или меньше
-нуля
.
Чтобы
выразить
коэффициент
асимметрии
в
виде
отвлеченного
числа,
определяют
частное
от
делени
'
я
f.L3
на
куб
стандарта
этого
же
распреде-
ления
.
Получающееся
число,
~бозначаемое
через
k
и
равное
~,
назы-
,~
"
а
вается
асимметрией,
ЩIИ
косостью,
изучаемой
СОВОI{УПНОСТИ.
Если
k >
О,
то
для
однове1JШИННЫХ
распределений
мода
меньше
среднего
арифмети
ческого
k <
О,
то
мода
больше
среднего
арифметического,
т,
е
.
распо
лагается
на
чертеже
правее
'
его
.'
,
-
"
RАМЕРАЛЬНЫЕ
МЕТОДЫ
ФАЦИАЛЬНОГО
.
АНАЛИЗА
595
Кроме
асимметрии
k,
за
меру
носости
принимают
таюне
число
Ма-М
О
.
а
= ,
которое
часто
называют
коэффициентом
асимметрии.
Оп
а
равен
нулю
для
симметричных
кривых
и
отличен
от
него
для
несимме
тричных
(фиг.
47-XIV).
Последним
показателем
харантера
распр еделения является
ЭYiсцесс.
Для
его
определения
предварительно
вычи
сляю
т
величину
четвертого
центрального
момента
Сам
же
эксцесс
равен
Е= 4-з.
(J
Эксцесс
равен
нулю
для
нормального
распре-
Q(
>0
MIIAlo
11<0
Фиг.
47-XIV.
Изменение
в
заимно
го
расположения
моды
и
средней
арифметической
при
различной
ве:
личине
коэффициента
асимм
е
трии
(по
В.
И
.
Рома">"
повскому)
.
деления.
Д
ля
кривых,
более
пологих
по
сравнению
с
нормаJIЬНОЙ,
он
отрицателен,
а
для
более
крутых
-
положителен
(фиг.
48-XIV).
ОхаРaI~теризованные
выше
стандартные
отклонения,
коэффициент
асимметрии
и
эксцесс
ВЫЧИСJIЯlОТСЯ
всегда
относительно
среднего
арифме
тич
еско
го.
Если
же
в
качестве
среднего
ра
зме
ра
взята
медиана,
то
для
Фиг.
48-XIV.
Сопоставление
формы
кривых,
ха
рактеризующихся
различным
эксцессом,
с
нормаль
ной
кривой
(по
В.
И.
Романовскому).
характеристики
распреде
ления
пользуются
ДРУГИМИ
коэффициентами,
а
энсцесс
.
не
вычисляется
вовсе.
В
рассматрива
емО
М
случае
для
оценки
степени
одно
образия
величины
членов
вместо
стандартного
ОТНЛо
нения
используют
отноше
ние
двух
квартилей,
опре
деляемых
по
нарастающей
кривой.
Квартили
пред
ставляют
собой
значения,
подразделяющие
данную
совонуцность
таним
образом,
что
1/4
всех
членов
имеет
большую
величину,
а
3/4
- .
меньшую,
и
наоборот.
Квартиль
;
лежащая
в
области
больших
значений,
называетСЯ
третьей
(Qз),
а
лежащая
в
области
меньших
размеров
-
первой
(Q1)'
Коэффициент
сортировки
8o,
хаРaI~теризующий
степень
однообразия
данной
совокупности,
при
использовании
системы
квартилей
равен
8 = l (
Qз
о
~
Q1
'
Коэффициент
сортиров
ни
для
положительных
величин
всегда
больше
единицы,
и
чем
больше
отклоняется
от
единицы
его
величина,
тем
менее
однообразна
соответствующая
совокупность.
Для
оцешш
асимметрии
данного
распределения
с
помощью
l\вартилей
вычисляется
коэффициент
асимметрии
Траска;
его
величина
определяетея
следующей
формулой
где
М
d -
медиана;
Ql
и Qз
-
квартили.
38*
8
-
QIQз
» -
ма
2

596
ФАЦИИ
И
МЕТОДЫ
ФАЦИАЛЬНОГО
АНАЛИЗА
П
рй
обработке
геологических
материалов
часто
возникает
не
'
обхо
димость
охарактеризовать
зависимость
между
значениями
двух
величин.
Подобные
связи
обычно
бывают
статистическими.
Это
значит,
что
каж
дому
заданному
значению
х
соответствует
не
одно
определенное
значение
У,
а
их
совокупность,
изменяющаяся
вместе
с
изменением
х.
Одним
из
наиболее
распространенных
видов
выражения
статистиче
ских
связей
является
корреляцио/-/,/-/,ая
связь,
под
которой
понимают
зави
симость
между
значениями
одной
величины
и
средними
другой.
Корреляционная
связь
может
быть
прямолинейной
или
криволиней
ной.
При
одной
и
той
же
форме
связи
сила,
или
степень
ее
отчетливости
может
быть
весьма
различной.
Особенно
широко
распространены
М
у
=ах+Ь
и
где
М
у
и
М
х
-
средние;
линейные
I<орреляции
вида
М
Х
=
су
+ d,
а,
Ь,
с
и
d -
некоторые
постоянные
числа.
Мерилом
силы
линейной
связанности
х
и
у
является
к,оэффициenm
корреляции.
При
отсутствии
линейной
связи
этот
коэффициент
равен
'
нулю,
но
при
увеличении
степени
их
линейной
связанности
он
возрастает
и
достигает
величины
+1,
если
при
увеличении
одной
величины
растет
и
другая,
или
-1,
если
зависимость
противоположна.
Величина
коэффициента
корреляции
определяется
по
формуле
Г
=
~ху-nvt,хVt.lI,
n
аха
у
-где
r -
коэффициент
корреляции;
~
ху
.-
сумма
произведений
частот
сравниваемых
величин,
под
разделенных
на
классы;
она
находится
по
специально
составленной
корреляционной
таблице;
Vt.
х
и
Vt.
11
~
первые
моменты
для
совокупностей
сопоставляемых
на
блюдений;
ах
и
ау
~
их
стандартные
отклонения;
n -
число
наблюдещrЙ
.
Корреляционные
уравнения,
характеризующие
линейную
статисти
,
чеtкую
зависимость
между
двумя
величинами,
принято
решать,
пользуясь
,
~ледуiOЩИМИ
форму
лами
у
= r
ау
(х-
М
х
)
+
М,},
ах
х=
r
ах
(у-М
у
)+
М
х
,
ау
где
МХИ
М
у
-
средние
арифметические
значения
данных
величин;
ахи
ау
-
их
стандартные
отклопенnя;
r -
коэффициент
корреляции.
Для
вычисления
коэффициента
корреляции
и решения
корреляцион
JIblX
уравнений
при
наличии
большого
количества
данных
составляют
специальные
таблицы.
Для
экономии
места
здесь
этот
способ
иллюстри
руется
на
примере
небольшой
совокупности
данных.
Допустим,
что
нужно
выяснить
наличие
корреляционной
связи
между
двумя
'
видами
величин,
значения
которых
приведены
в
табл.
15-XIV.
В
каждой
клетке
основной
части
таблицы
отмечается
количество
случаев,
когда
величины
обоих
коэффициентов
изменяются
в
тех пределах,

КАМЕРАЛЬНЫЕ
МЕТОДЫ
ФАЦИАЛЬНОГО
АНАЛИЗА
Таблица
15-XIV
Значения
среднего
ариФметического
раамера
зерен
и
коэффициента
сортировки
.
Средний
ар~ф-
Ноэффици-
Средний
арифме-
Ноэффици~
метическии
ент сорти-
тическuй
размер
еит
сорти-
размер
зерен
РОБКИ
зерен
РОБКИ
.
0,180 0,115 0,247
I
0,131
0,285 0,035
0,312
0,115
-
- 0,212
0.135 0,305 0,126
0,322
0,060
0,360 0,095
0,326 0,080
0,238
0,160
0.312
0,140 0,295
0,110
0,355
0,062 0,326
0,105
0,242
0,115 0,290 0,130
0,262 0,080
0,363
0,132
0,330 0,085
0,248
0,178
0,352 0,070
0,276 0,090
0,271 0,110
0,330 0,120
0,338
0,093
0,253 0,080
0,277
0,085
0,127 0,145
0,315
0,095
0,371 0,074
0,360 0,072
I
0,382 0,081
0,380 .
0,0.51
0,361 0,060
0,396
0,093
0,395 0,085
Щ7
ко.то.рые
предусмо.трены
данно.Й
вертикальной
и
го.ризо.нта
J
IЬНо.Й
стро.ками
таблицы.
Так,
например,
в
табл.
16-XIV
в
о.дно.м
лишь
случае
при
сред
нем
арифМетическо.м,
изменяющемся
0.1'
0,175
до.
0,200,
ко.эффициент
со.р
тиро.вки
меняется
о.т
0,100
до.
0,125.
3а
пределами
о.сно.вно.й
части
таблицы
в
третьей
снизу
и
в
трет;ье
й справа
графах
приводится общее
ко.личестВо
величин,
вхо.дящих
в
данный
интервал значений
среднего.
размера
и
к:оэф
фициента
со.ртиро.вки.
Сумма
этих
чисел
по.
го.ризо.нтали
и
вертикали,
о.чевидно.,
до.лжна
быть
равна
но.личеству
пар
исхо.дных
·
значений,
пере
численных
в
табл.
16-XIV.
В
данно.м
случае
она
равна
36.
По.сле
это.й
про.верки
намечаются
графы,
характеризующиеся
наибо.ль
шим
ко.личество.м
случаев,
а
о.стальные
графыI
по.следо.вательно.
нумеруются
о.т
них
со.
знано.м
плюс
или
минус,
в
зависимо.сти
о.т
то.го.,
где
о.ни
распо.л
а
гаются:
в о.бласти
бо.льших
и
ли
меньших
значений
'
.
Эта
'
нумерация
при
ведена
во.
вто.ро.й
снизу
И
вто.ро.й
справа
графах
таблицы.
В
данно.м
случае
для
среднего.
размера
зерен
центрально.Й
будет
графа,
со.о.тветствующая
интервалу
0,350-0,375
мм,
а
для
ко.эффициента
со.ртиро.вни
-
графа
0,075-0,100.
'
По.сле
это.го.
про.и
зво.дится
умно.жение
числа
наблюдений,
о.тмеченных
в
клетках
ко.рреляцио.нно.Й
таблицы, на
множитель,
представляющий
со.бо.Й
про.изведение
ноо.рдинат
это.Й
нлетни,
выраженных
в
интервалах
о.ткло.нениЙ
от
центральных
граф.
Эти
мно.жители
п
·
о.назаны
в
нижнем
право.м
углу
каждо.Й
нлетки.
Сумма
ито.го.вых
про.изведениЙ
для
наждо.Й
вертикально.Й
и
го.ризо.н
тальных
граф
выписана
в
по.следних
вертикально.Й
и
го.ризо.нтально.Й
графах
таблицы.
Общая
сумма
цифр
во.
всех
графах
до.лжна
бытьо.дно.Й
и
то.Й
же.
В
данно.м
случае
о.на
равна
89.
Далее
для
каЖДQГQ
из
НQэффициеНТQВ
вычисляется
первый
мо.мент
QТНQсительно.
УСЛQВНо.го.
среднего.
и
стандаРТНQе
отнлонение
табл.
17-
x1v
и
18-XIV.
