Roy K.K. Potential theory in applied geophysics

Подождите немного. Документ загружается.

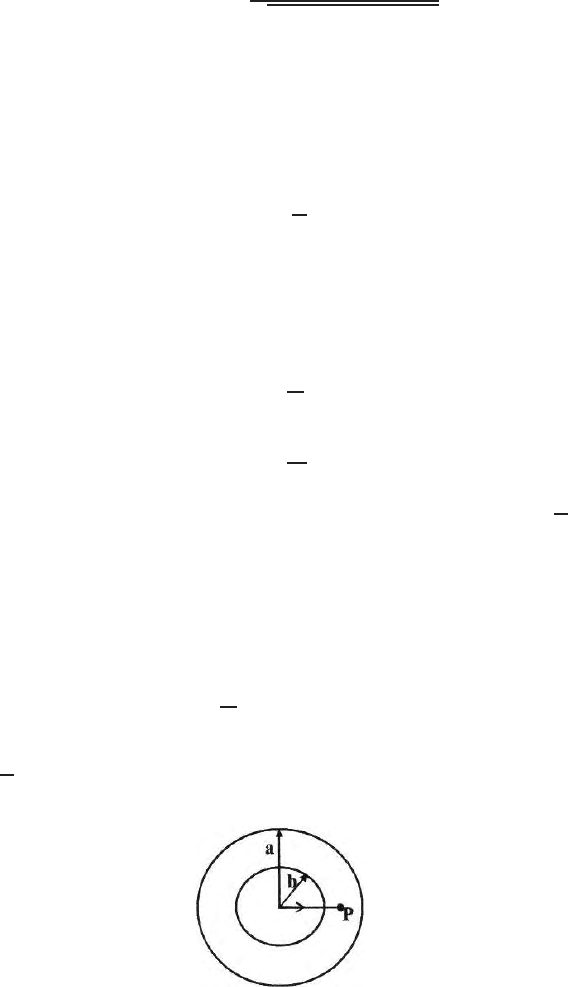
3.11 Gravitational Potential at a Point due to a Spherical Bo dy 59

= −G

2π



ρa

sin θdθdadψ

√

+ R

− 2aR cos θ

(3.48)

where

− 2aR cos θ

and

rdr = aR sin θ d θ.

= −2πGρ



dr. (3.49)

Case I

When the point P is outside the sphere

= −2πGρ

R+a



R−a

= −4πGρ

da. (3.50)

Since the total mass of the shell = 4πρa

da, the potential φ

= −G

as if

the mass of the spherical shell is put at the centre.

Case II

If the point of observation P is inside (Fig. 3.12)

= −2πGρ

a+R



a−R

dr = −4πGρ ada (3.51)

= −G

where m is the total mass of the shell.

Fig. 3.12. Computation of potential at a point P within a spherical shell of outside

radius a and inside radius b

60 3 Gravitational Poten tial and Field

When the outer and inner radii of the shell are respectively ‘a’ and ‘b’, the

mass is M =



− b



ρ.

Therefore the potential outside is

= −

4πGρ



da = −

4π

Gρ

− b

(

= −G

. (3.52)

The potential at internal point

= −4πGρ



ada = −2πGρ



− b



. (3.53)

Since a

−b

= Constant, the ﬁeld inside



∂ρi

∂r



is zero for the solid sphere.

=2πGρa

= Constant. Therefore, the ﬁeld inside will be zero.

The gravitational potential at any point inside a solid body is determined

by the mass internal to the point inside the sphere of radius ‘a’. The mass out-

side does not have any eﬀect on the potential. It shows that the gravitational

ﬁeld at the centre of the earth is zero.

Case III

When the point of observation ‘P’ is within the spherical shell

For the point P outside, the potential

πGρ

− b

(3.54)

and for inside

=2πGρ(a

− R

). (3.55)

So the total p otential φ in the material itself is

total

= φ

+ φ

= −

πGρ



− b



− 2πGR



− R



= −4πGρ



−

. (3.56)

The gravity ﬁeld

= −

∂R

= −

πGρ



−

+ R

= −

πGρ



−

− b

. (3.57)

We can now examine the continuity of the potentials at the boundaries

(i) when R < b

=2πGρ



− b



(3.58)

3.11 Gravitational Potential at a Point due to a Spherical Bo dy 61

Fig. 3.13a. Potential at a point inside a spherical shell due to mass of the spherical

shell

(ii) when b < R < a

= −4πGρ



−



(3.59)

(iii) when R > a

= −

πGρ

− b

. (3.60)

When R = b, potentials for case (i) and (ii) becomes 2πGρ(a

− b

)and

when R = a, the potentials for case (ii) and (iii) becomes

−

πρG

− b

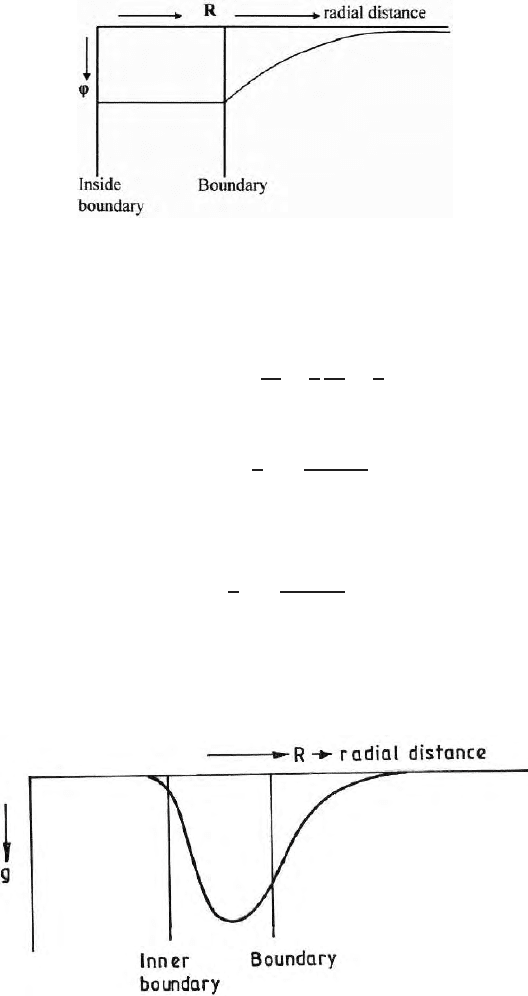
Therefore, the potential remains same inside the boundary. As soon as the

point of observation comes out on the surface, t he potential and ﬁeld intensi-

ties decreases with distance as follows (Fig. 3.13a and Fig. 3.13b):

Fig. 3.13b. A curtoon of variation of ‘g’ both outside and inside the air-earth

b oundary, g = 0 at the centre of the earth as well as in the outer space;maximum

value of g is at a certain depth from the surface

62 3 Gravitational Poten tial and Field

(i) for R < b

(ii) for b < R < b

= −

πGρ

− b

(3.61)

Both potential and gravitational ﬁeld are continuous across the boundary.

3.12 Gravitational Attraction on the Surface due

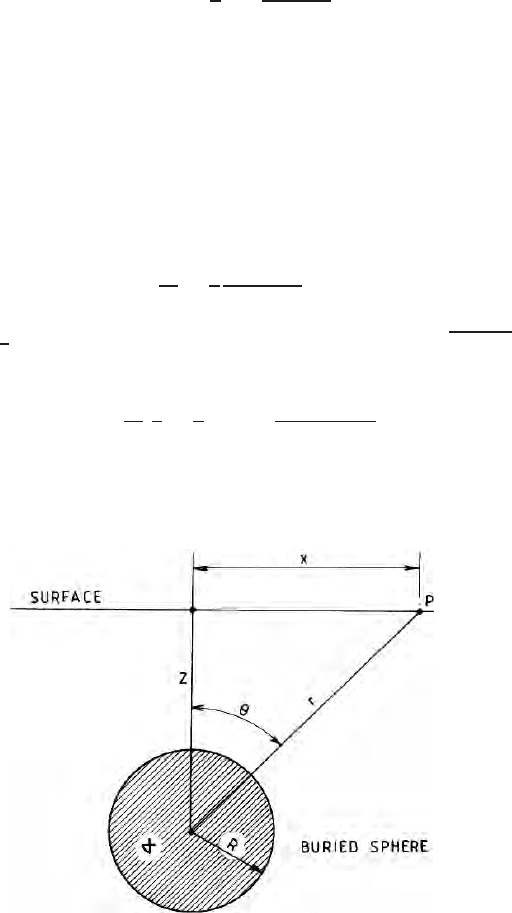
to a Buried Sphere

Gravitational attraction upon unit mass at a p oint P on the surface due to a

buried sphere of radius R, density σ and buried at a depth z is given by

πGR

)

(3.62)

where M( =

πR

σ) is the mass of the spherical body and r =

√

.The

vertical component of the gravitational attraction will be equal to (Fig. 3.14)

πGR

σ.

)

3/2

. (3.63)

Gravitational force will be maximum at the origin i.e., at z = 0 and x = 0

on the surface. The value will die down symmetrically on both the sides of

Fig. 3.14. Gravitational anomaly on the surface due to a buried spherical bo d y of

radius R

3.13 Gravitational Anomaly due to a Body of Trapezoidal Cross Section 63

the spherical mass with increasing distance x from the origin. For further

studies the readers are referred to the works o f Blakely(1996), Talwani and

Ewing(1961), Radhakrishnamurthy(1998) Telford et al (1976) and Dobrin and

Savit(1988).

3.13 Gravitational Anomaly due to a Body

of Trapezoidal Cross Section

Gravitational attraction on the surface at a point P due to a body of rect-

angular cross section present within the depth extent of z

and z

> z

)

(Fig. 3.15) is given by

∆g

=2Gρ



zdxdz

(3.64)

where G is the universal gravitational constant a nd ρ is the density contrast

of the body with the surrounding host rocks

For a two dimensional body of trapezoidal cross-section as shown in the

Fig. 3.15.

RQ = rdθ =dxSinθ (3.65)

The gravitational anomaly due to a two dimensional body of trapezoidal cross

section is given by

∆g

=2Gρ



dx dz. (3.66)

Since z = rSinθ,and

rSinθ

Sinθ

we get

∆g

=2Gρ



Sinθ

dx dz (3.67)

=2Gρ



dθ dz. (3.68)

Fig. 3.15. Gravitational anomaly due to a two dimensional bod y of trap ezoidal

cross section

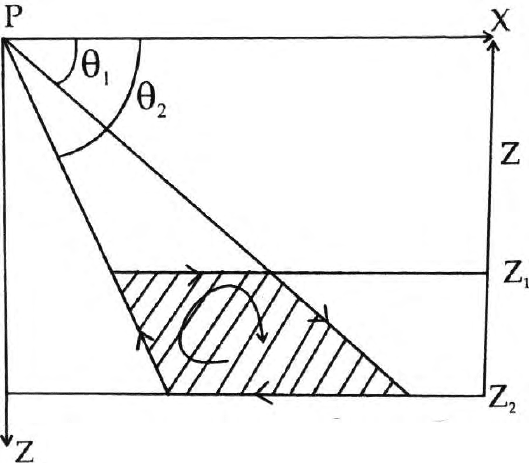
64 3 Gravitational Poten tial and Field

Fig. 3.16. Enlarged view of a trapezoidal cross section of a body and the direction

of line integral

Line integral along the trapezoidal cross section (Fig. 3.16) is given by



θdz =



θdz +



,θ

θdz +



θdz +



,θ

θdz (3.69)

=0+θ

− z

)+0+θ

− z

)

=(z

− z

)(θ

− θ

). (3.70)

3.13.1 Special Cases

Case I Gravitation Attraction Due to a Two Dimensional

Horizon tal Slab

Figure 3.17 shows the geometry of the problem. Gravitational anomaly at the

point P.

∆g

=2Gρ

⎡

⎣



θdz +



θdz +



θdz +



θdz

⎤

⎦

(3.71)

3.13 Gravitational Anomaly due to a Body of Trapezoidal Cross Section 65

Fig. 3.17. Gravitational attraction at the point P due to a two dimensional hori-

zontal slab

=2Gρ

⎡

⎣



0,z

θdz +

π,z



π,z

θdz +

π,z



π,z

θdz +

π,z



π,z

θdz

⎤

⎦

(3.72)

=2Gρ[0 + π(z

− z

)+0+0]

=2πGρ(z

− z

). (3.73)

Case II Gravitational Anomaly Due to a Fault with a Small Throw

Figure 3.18 shows the geometry of the ﬁgure. The gravitational anomaly at

the point P is

∆g

=2Gρ

⎡

⎣



0,z

θdz +



,θ

θdz +



,θ

θdz +



θdz

⎤

⎦

(3.74)

=2Gρ[0 + θ

− z

) + 0 + 0] (3.75)

=2Gρθh=2Gρhtan

−1

. (3.76)

Fig. 3.18. Gravitational anomaly due to a fault with a small throw

66 3 Gravitational Poten tial and Field

Case III Gravitational Anomaly due to a Body of Rectangular

Cross Section

Figure 3.19 Show the geometry of the problem. Gravitational anomaly at a

point P is given by

∆g

=2Gρ

⎡

⎣



θdz +



θdz +



θdz +



θdz

⎤

⎦

(3.77)

=2Gρ

⎡

⎣



tan

−1

dz + 0 +



tan

−1

⎤

⎦

(3.78)

=2Gρ [z

(θ

− θ

)+z

(θ

− θ

)

−





. (3.79)

Since



tan

−1

dx = x tan

−1

−

ln(a

)

Case IV Gravitational Attraction at a Point on the Surface due to

aThinPlate

Figure 3.20 shows the geometry of the problem. Gravitational anomaly at the

point P due to the thin plate of ﬁnite length is given by

∆g

=2Gρ [z

(θ

− θ

)+z

(θ

− θ

)]

=2Gρ [∆˙z(θ

− θ

)]

=2Gρtθ (3.80)

where θ is the angle made by the plate at the point of observation P. t (= ∆z)

is the thickness of the plate.

Fig. 3.19. Geometry of the buried prism of rectangular cross section and the point

of observation on the surface

3.13 Gravitational Anomaly due to a Body of Trapezoidal Cross Section 67

Fig. 3.20. Geometry of a buried thin slab and the point of observation on the

surface

Case V Gravitational Attraction at a Point on the Face of a Two

Dimensional Ridge

Figure 3.21 shows the geometry of the problem. Gravitational attraction at a

point P on the face of a two dimensional ridge is g iven by

∆g

=2Gρ

⎡

⎣

⎧

⎨

⎩

∞



θdz +



,∞

θdz +



∞,z

θdz +



θdz

⎫

⎬

⎭

⎧

⎨

⎩



θdz +

∞



θdz +



,∞

θdz +



0,z

θdz

⎫

⎬

⎭

⎤

⎦

(3.81)

=2Gρ [{0+2π(z

− z

)+0+(2π − α)(z

− z

)}

+ {(π − α)(z

− z

)+0+0+0}] (3.82)

=2Gρ[(z

− z

)(2π − 2π + α)+(π − α)(z

− z

)] (3.83)

=2Gρ[α(z

− z

)+π(z

− z

)] (3.84)

=2Gρα(z

− z

) − 2πGρ(z

− z

). (3.85)

Fig. 3.21. Geometry of a ridge and the point of observation on the ridge surface

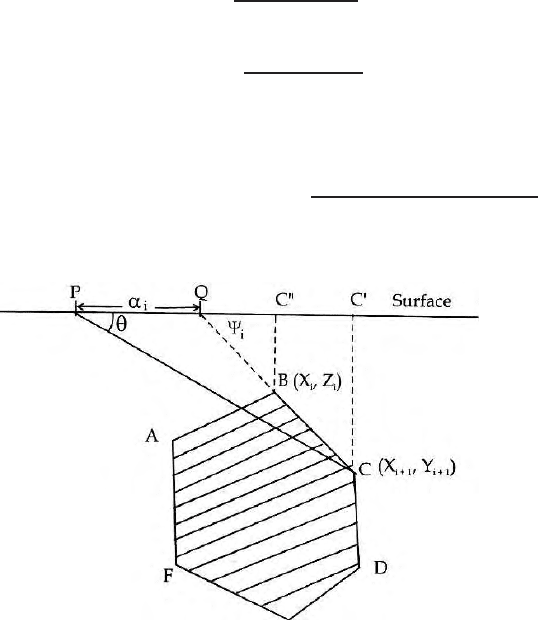
68 3 Gravitational Poten tial and Field

Case VI Gravitational Attraction on the Surface due to a Buried

Two Dimensional Body of Hexagonal Cross Section.

Figure 3.22 shows the geometry of the problem. Here gravitational attraction

at a point P due to an elementary strip of hexagonal cross section is given by

∆g



θdz. (3.86)

In segment BC

z=xtanθ =(x− a

)tanψ

=xtanψ

− a

tan ψ

. (3.87)

From the (3.87) we get

x=a

tan ψ

/(tan ψ

− tan θ) (3.88)

and

z=xtanθ =

tan θ tan ψ

tan ψ

− tan θ

, (3.89)

therefore

∆g

=2Gρ



tan θ tan ψ

tan ψ

− tan θ

dθ. (3.90)

The total gravity anomaly will be

∆g = ∆g

+∆g

(3.91)

∆g

sin φ

cos φ



− θ

i+1

+tanψ

cos θ

(tan θ

− tan ψ

)

cos θ

i+1

(tan θ

i+1

− tan ψ

)

(3.92)

Fig. 3.22. Geometry of a buried two dimensional cylindrical structure of hexagonal

cross section and the point of observation on the surface