Roy K.K. Potential theory in applied geophysics
Подождите немного. Документ загружается.


3.5 Gravitational Field due to a Line Source 49
F
x
=
λdξ
(x −ξ)
2
+y
2
.
x −ξ
(x − ξ)
2
+y
2
(3.15)
and
F
y
=
λdξ
(x −ξ)
2
+y
2
.
y
(x − ξ)
2
+y
2
. (3.16)
Therefore, the total fields F
x
and F
y
for the entire linear mass are given by
F
x
= λ
a
−a
(x − ξ)dξ
(x − ξ)
2
+y
2
3/2
(3.17)
F
y
= λ
a
−a
ydξ
(x − ξ)
2
+y
2
3/2
(3.18)
Let
cos α =
y
(x − ξ)
2
+y
2
1/2
and
−sin α dα = −
2y (x − ξ)dξ
2
(x − ξ)
2
+y
2
3/2
.,
therefore
F
x
=
λ
y
α
2
α
1
sin αdα=
λ
y
(cos α
2
− cos α
1
)
=
λ
y
⎡
⎣
y
(x + a)
2
+y
2
−
y
(x −a)
2
+y
2
⎤
⎦
(3.19)
Similarly for
F
y
= λ
⎡
⎢
⎣
ydξ
(x −ξ)
2
+y
2
3/2
⎤
⎥
⎦
(3.20)
Let
tan α =
x −ξ
y
, and sec
2
αdα = −
dξ
y
.
since sec
3
α =
1
y
3
(x − ξ)
2
+y
2
3/2
,weget
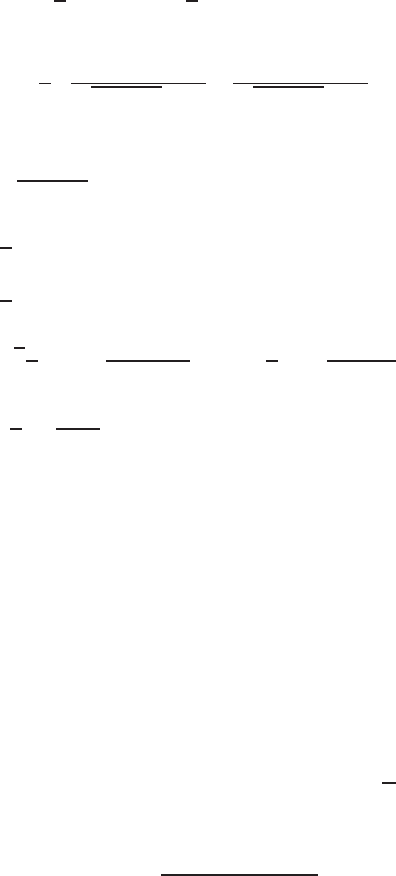
50 3 Gravitational Poten tial and Field
F
y
= −
λ
y
α
1
α
2
cosαdα =
λ
y
[sin α
1
− sin α
2
]
=
λ
y
⎡
⎣
x −a
(x −a)
2
+y
2
−
x+a
(x + a)
2
+y
2
⎤
⎦
(3.21)
Now
F=
F
2
x
+F
2
y
=
λ
y
[2 −2cosα
1
cos α
2
− 2sinα
1
sin α
2
]
1/2
=
λ
y
[2 −2cos(α
1
− α
2
)]
1/2
=
√
2
λ
y
2sin
2
(α
1
− α
2
)
2
1/2
=2
λ
y
sin
α
1
− α
2
2
=2
λ
y
sin
∧
APB
2
(3.22)
Therefore, the direction of the gravitational force of attraction is along the
bisector of the triangle
∧
APB.
3.6 Gravitational Potential due to a Finite Line Source
Although once field due to a finite line source is known, the gravitational
potential at a point is known also. However a separate section is given to
highlight a few points of principle.
A line source AB of length L is taken along the z-direction (Fig. 3.5). In
a cylindrical co-ordinate, the potential will not depend upon the azimuthal
angle ψ but on r a nd z. Take a small element dζ.Itsmassisλdζ wher e λ
is the linear density. Since the gravitational potential is −G
m
R
where m a nd
r are respectively the mass and distance of the point of observation. We can
write
φ = −Gλ
l
−l
dζ
r
2
+(z −ζ)
2
1/2
(3.23)
Let
z − ζ =rtanθ, so
−dζ =rsec
2
θdθ
3.6 Gravitational Potential due to a Finite Line Source 51
Fig. 3.5. Gravitational potential at a point due to a finite line source
Therefore
φ =Gλ ln [sec θ +tanθ]
l
−l
φ =Gλ
⎡
⎣
ln
⎧
⎨
⎩
z −l
r
+
r
2
− (z −l)
2
r
⎫
⎬
⎭
− ln
⎧
⎨
⎩
z+l
r
+
r
2
+(z+l)
2
r
⎫
⎬
⎭
⎤
⎦
φ = −Gλ ln
(z + l) +
r
2
++(z+l)
2
(z − l) +
r
2
++(z− l)
2
(3.24)
When φ = Constant
K=e
−φ/Gλ
=
z+l+
r
2
+(z+l)
2
z −l+
r
2
+(z− l)
2
(3.25)
This is an equation for the equip o tential surface and (3.25) can be rewritten
with a few steps of algebraic simplification in the form.
(K −l)
2
(K+l)
2
.
z
l
2
+
(K −l)
2
4K
.
r
L
2
=1. (3.26)
This is an equation of an ellipse. The semi major and minor axes are respec-
tively given by
K+1
K −1
.land
2
√
K
K −1
l.
The eccentricity is e =
1 −
b
2
a
2
and the foci are at ±l.
52 3 Gravitational Poten tial and Field
The field components are
f
r
= −
∂φ
∂r
=Gλ.
1
r
⎡
⎣
z+l
r
2
+(z+l)
2
−
z − l
r
2
+(z− l)
2
⎤
⎦
(3.27)
f
z
= −
∂φ
∂z
= −Gλ
1
r
⎡
⎣
r
r
2
+(z+l)
2
−
r
r
2
+(z− l)
2
⎤
⎦
(3.28)
The total field of f =
f
2
r
+f
2
z
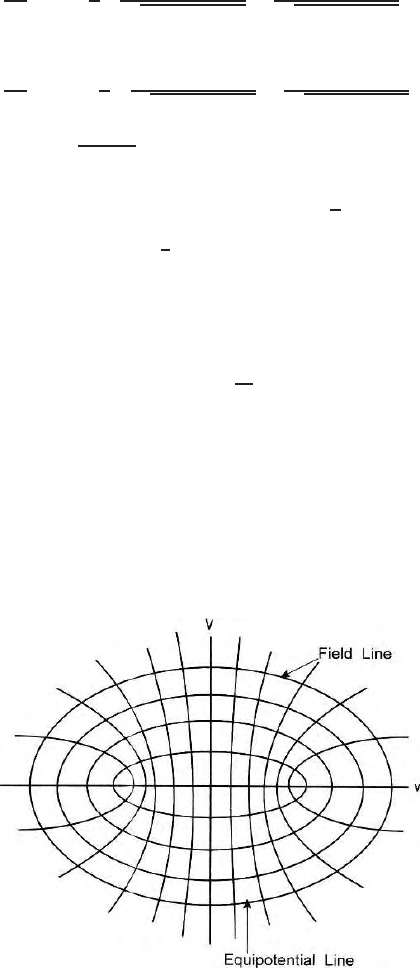
describes hyperb o las (Fig. 3.6). For a very long
wire where
l → α, g
z
=Oandg
r
= −Gλ
2
r
(3.29)
Here the field is proportional to
1
r
. Hence the potential is
φ = λ
gdr + Constant
=2Gλ ln r + Constant
= −2Gλ ln
r
0
r
1
(3.30)
It implies that the potential becomes zero at infinity. Therefore for a line
source p o tential is logarithmic potential and field varies inversely with dis-
tance. For a finite line source the equipotentials are ellipses and the eccentric-
ity of the ellipse die down with distance from the source. At infinite distance
the eccentricity of the ellipse will be zero and th e ellipse will turn into a circle.
The field lines will be radial For an infinitely long line source the field lines
and equipotential lines will form a square or rectangular grids
Fig. 3.6. Field lines and equipotential lines due to a line source of finite length
3.7 Gravitational Attraction due to a Buried Cylinder 53
3.7 Gravitational Attraction due to a Buried Cylinder
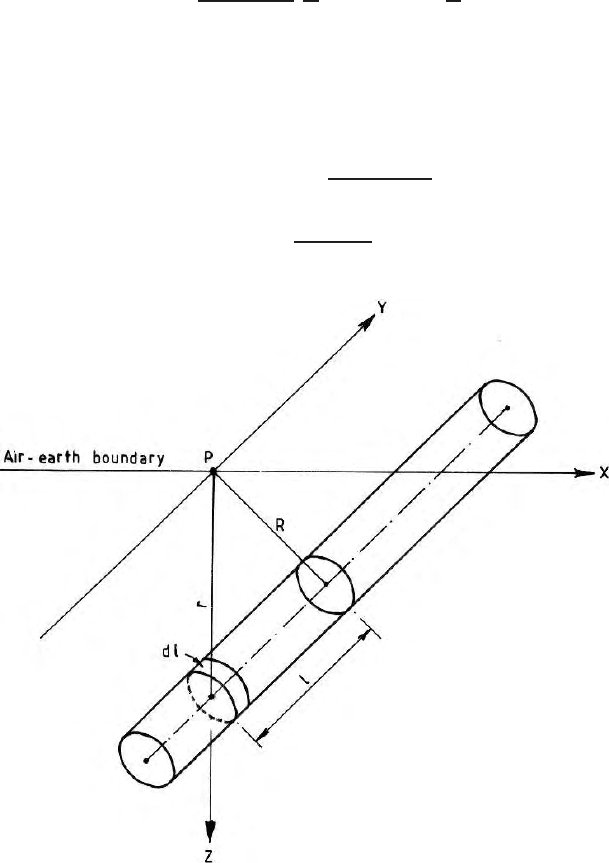
Vertical component of gravitational attraction at unit mass at the point of
observation ‘P’ due to a small element ‘dl’ at a distance ‘l’ from ‘Q ’ , the
shortest distance of the cylinder from the point of observation is (Fig. 3.7)
dg
z
=
GdmSinθ
r
2
.
R
r
=Gλ dl Sinθ.
R
r
. (3.31)
Here dm is the elementary mass of the thin strip dl, λ is the linear density of
the cylinder and is equal to πa
2
λ for unit length where ‘a’ is the radius of the
cylinder and G is the universal gravitational constant. Vertical gravitational
attraction due to a cylinder of infinite length is
g
z
=GλSinθR
α
−α
dl
(R
2
+l
2
)
3/2
(3.32)
=2Gπa
2
λ
z
(x
2
+z
2
)
. (3.33)
Fig. 3.7. Gravitational anomaly on the surface due to a buried cylindrical body of
finite length
54 3 Gravitational Poten tial and Field
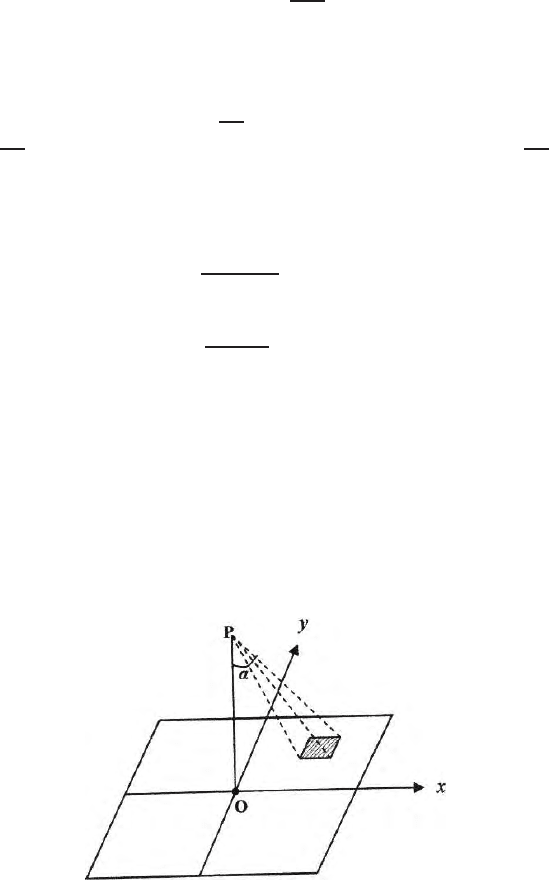
3.8 Gravitational Field due to a Plane Sheet
Let us assume a plane sheet in the xy plane and is symmetrical around the
axis OP vertical to the plane of the paper (Fig. 3.8).We assume an elementary
area ds on the plane sheet. Let
σ =Lim
∆S→0
∆m
∆S
where ∆s is the surface area of an infinitesimally small surface area in the
plane sheet and ∆m be its mass.
For a small area ds, the mass of the area is σds. The gravitational field
due to this small element at P is
σds
r
2
. Vertical component of this fi eld is given
by f
z
=
σds
r
2
cos α and the component at right angles to z direction is
σds
r
2
sin α.
Since the point of observation P is sy mmetrically placed with respect to the
plate, the vertical components of the field will get added up. The components
perpendicular to the z-direction will get cancelled. The vertical component of
the field is
f
z
=
σds cos α
r
2
=
σdω = σω (3.34)
where
ds cos θ
r
2
=dω.
Here dω is the solid angle subtended by the elementary mass at the P, ω is
the total solid angle subtended by the plate at the point P. The field at the
point P is equal to the density multiplied by the solid angle subtended at the
point P. For an infinitely large sheet ω =2π.
f
z
=2πσ (3.35)
and. the field is independent of the distance of the point of observation from
the plate.
Fig. 3.8. Gravitational field on the vertical axis of a square horizontal plate
3.9 Gravitational Field due to a Circular Plate 55
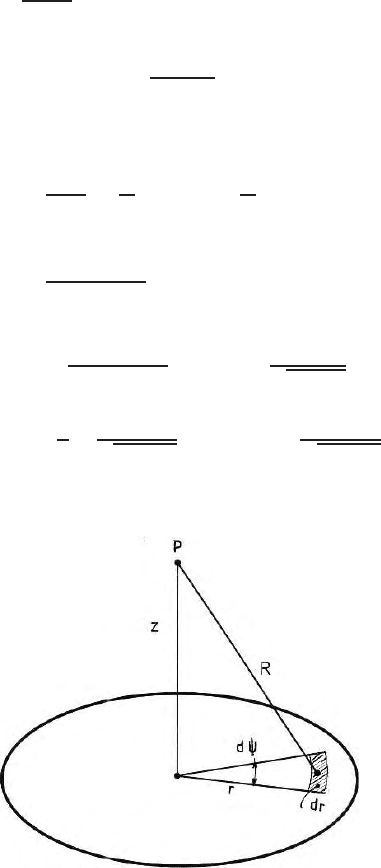
3.9 Gravitational Field due to a Circular Plate
In this section, we shall derive the expression for the gravity field due to
circular plate. Let us choose the polar co-ordinate (r, ψ). The field at a point
P along a vertical line crossing the plane of the plate at right angles for the
elementary mass is
σrdrdψ
R
2
.whereσ is surface density (Fig. 3.9). Therefore,
the vertical component of the field is
∆f
z
=
σrdrdψ
R
2
cos α. (3.36)
Other components will vanish because of symmetry of the problem. Hence
f
z
=
a
o
2π
o
σrdr
R
2
dψ.
z
R
∵ cos α =
z
R
, R
2
=r
2
+z
2
=
a
o
2π
o
σzrdrdψ
(r
2
+z
2
)
3/2
(3.37)
=2πσz
a
o
rdr
(r
2
+z
2
)
3/2
=2πσz
−
1
√
r
2
+z
2
a
o
=2πσz
1
z
−
1
√
z
2
+ a
2
=2πσ
1 −
z
√
z
2
+ a
2
.
Fig. 3.9. Gravitational field on the vertical axis of a horizontal circular plate
56 3 Gravitational Poten tial and Field
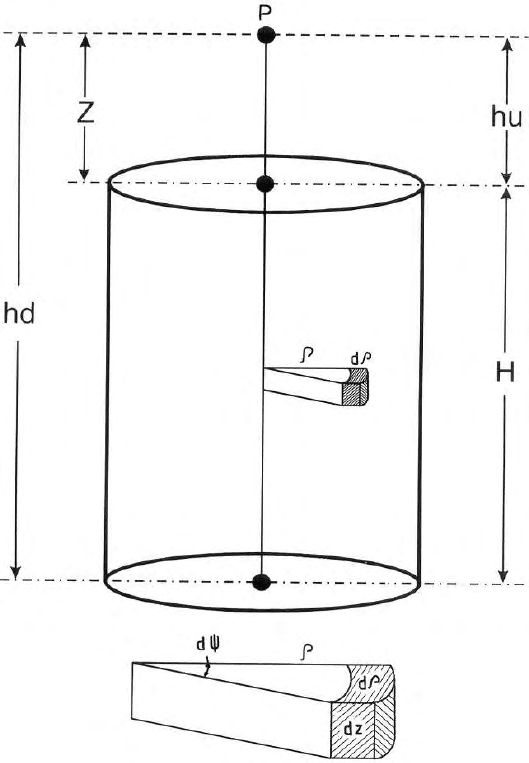
3.10 Gravity Field at a Point Outside on the Axis
of a Vertical Cylinder
To compute gravitational field at a p oint P on the axis of a cylinder at a
po int ou tside it, we assume an elementary mass σρdρdψ dz inside the cylinder
(Fig. 3.10). Here R is the radius of the cylinder. h
u
and h
d
are the depths,
from the surface, to the top and bottom planes of a cylinder of length or
height H. σ is the volume density of mass.
Fig. 3.10. Gravitational field on the axis of a vertical solid cylindrical body at a
point outside the body

3.10 Gravity Field at a Point Outside on the Axis of a Vertical Cylinder 57
The gravitational attraction due to an elementary mass at the point P
outside the cylinder and on its axis is
dg =
Gdm
r
2
=G
σρdρdψdz
r
2
(3.38)
where dv = ρdρdψdz. ρ is the radial distance of the elementary mass from
the axis of the cylinder. Since only the vertical component is of interest.
So
dg
z
=dgcosθ =dg
z
r
=
Gσρdρ.dψzdz
r
3
. (3.39)
The total gravitational attraction of the cylinder at the point P is given by
∆g
z
=Gσ
R
ρ=o
hd
hu
2π
ψ=o
ρdρdψzdz
(ρ
2
+z
2
)
3/2
(3.40)
⇒ Gσ
2π
o
dψ
hd
hu
zdz
R
o
ρdρ
(ρ
2
+z
2
)
3/2
(3.41)
⇒ 2πGσ
hd
hu
zdz
R
o
ρdρ
(ρ
2
+z
2
)
3/2
⇒ 2πGσ
hd
hu
zdz
−
1
(ρ
2
+z
2
)
1/2
R
o
(3.42)
⇒ 2πGσ
⎡
⎣
hd
hu
dz −
hd
hu
zdz
(R
2
+z
2
)
⎤
⎦
R
o
⇒ 2πGσ
hd
hu
zdz
1
z
−
1
√
R
2
+z
2
⇒ 2πGσ
(h
d
− h
u
) −
R
2
+h
2
d
+
R
2
+h
2
u
(3.43)
So
∆g
z
=2πGσ
H −
R
2
+ h
2
d
+
R
2
+ h
2
u
. (3.44)
Case I
If the p oint of observation is located right on the upper surface of the cylinder.
Then h
u
=O, h
d
=Hand

58 3 Gravitational Poten tial and Field
∆g
z
=2πGσ
H −
R
2
+H
2
+R
. (3.45)
Case II
When R >> H
∆g
z
=2πGσH. (3.46)
This is the expression for Bouguer gravity anomaly due to the plate.
Case III
When R << H
∆g
z
=2πGσR. (3.47)
This is the expression for a gravitational field for H →∞. i.e., for colum-
nar structure s like volcanic pipe or a long cylindrical intrusions like mantle
xenoliths etc.
3.11 Gravitational Potential at a Point due
to a Spherical Body
Let a small e lementary circular shell is assumed in a spherical body at a
distance ‘a’ from the centre of the sphere (Fig. 3.11).The point of observation
P is at a distance R from the centre of the sphere and ‘r’ from the elementary
mass.
So
dm = ρa
2
sin θ d θ da d ψ
where ρ is the density of the material of the spherical body (spherical shell or
solid sphere). The gravitational potential at a point P is given by
Fig. 3.11. Gravitational potential and field at a point P outside a spherical body
(solid or hollow)
