Roy K.K. Potential theory in applied geophysics

Подождите немного. Документ загружается.

4.6 Electric Displacement ψ and the Displacement Vector D 79

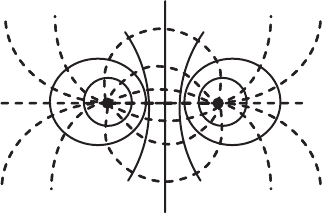
Fig. 4.4. Shows the electrostatic ﬁeld due to two opposite charges in a homogeneous

and isotropic medium

4.5 El ectric Flux

When an isolated positive or negative charge is placed in a homogenous and

isotropic dielectric medium , ﬁeld lines originating from the sour ce spread

along the radial direction with the charge at the centre (Fig. 2.3). In the case

of a negative charge the ﬁeld lines will converge radially to the negative charge.

When a positive and a negative charge is placed in a dielectric medium the

ﬁeld lines will start from a positive charge and will end up in a negative charge

as shown in Fig. 4.4. The ﬁeld lines are the lines of forces or the ﬂux lines. The

important properties of these electric ﬂux are (i) these ﬂuxes are independent

of the medium, (ii) the magnitude of these ﬂuxes is solely depend ent upon

the strength of the charge from which the ﬂux lines come out, (iii) the electric

ﬂux density must be inversely proportional to the square of the distance if the

ﬂux source is covered by a bounded domain say a sphere. The ﬂux lines will

be perpendicular to the spherical surface.

4.6 Electric Displacement ψ and the Displacement

Vector D

Faraday’s famous experiment o n movement of electrostatic charges in diﬀerent

spherical shells is as follows: A sphere with charge q is placed within another

spherical shell without touching it. The outer sphere is momentarily earthed

and when the inner sphere is removed, the charge on t he outer shell is found to

be exactly the same as that in the inner sphere but of opposite sign. It is true

for all sizes of the sphere and for all dielectric constants of the media. There is

a displacement of charges from the inner sphere to those in the outer sphere.

The amount of displacement depends only upon the magnitude of the charge

q. Thus the displacement is in Coulomb i.e., Ψ = q. The electric displacement

pe r unit area at any point on a spherical surface of radius ‘r’ is the electric

displacement density



D. It is a vector because there is a deﬁnite direction for

this displacement. So,

80 4 Electrostatics



D =

4πr

(4.10)

The unit is in Coulomb/meter

. The displacement per unit area a t any point

depen d s upon t he direction of the area and it is normal to the surface elements.

This displacement is along the direction of the ﬁeld in a homogeneous and

isotropic dielectrics. Therefore we can again write,



4πr

.r (4.11)



D=∈



E. (4.12)

The vector D is also called displacement vector. We can deﬁne the ﬂux Ψ =

D.ds where ds is the diﬀerential surface elements on the surface S.

In an anisotropic dielectric, the electrical permittivity becomes a tensor

and the connecting relation between D and E can b e expressed as

=∈

+ ∈

=∈

+ ∈

=∈

+ ∈

and in the matrix form

⎡

⎣

⎤

⎦

⎡

⎣

∈

⎤

⎦

⎡

⎣

⎤

⎦

(4.13)

4.7 Gauss’s Theorem

The total normal induction or total displacement of electric ﬂux through any

closed surface, which enclosed the charges, is equal to the amount of charge

enclosed. From Fig. 4.5, the displacement or electric ﬂux through the elemen-

tary surface ds is

dΨ = D ds cos θ (4.14)

where θ is the angle between D and n.wheren is normal to the surface ds.

The total normal in duction through the entire surface is given by

Ψ=





Ddscosθ (4.15)

where the integration is over the whole surface.

Solid angle dω is (Fig. 4.6)

dω =

ds cos θ

(4.16)

and,

4.7 Gauss’s Theorem 81

Fig. 4.5. Shows the normal induction through the surface ds when a charge q is

b ounded by the surface S

ψ =



d̟. (4.17)

Substituting the value of D from (4.6), we get

ψ =

4π



dω. (4.18)

Since the total solid angle subtended at the point O (occupied by the charge

q) by the closed surface is 4π, therefore

ψ =q. (4.19)

If there be n number of dielectric charge q

within the enclosed volume, the

total ﬂux on the surface will be,

ψ =



i=1

. (4.20)

If the charges are distributed throughout the volume and ρ is the volume

density of charge then the total normal induction through the surface is

ψ =



ρ dv. (4.21)

Fig. 4.6. Shows the solid angle subtended at the point o due to the surface ds

82 4 Electrostatics

Now (4.18) can b e written as,

Ψ=



D.ds. (4.22)

From (4.22), we can write,





D.ds=



ρdv. (4.23)

Applying Gauss’s divergence theorem, we can write



div



Ddv =





D.n.ds =



ρdv (4.24)

div



D=∇.



D=ρ. (4.25)

4.8 Field due to an Electrostatic Dipole

Both dipoles and bipoles consist of two poles. The diﬀerence lies in the distance

between the two poles. In an electrostatic dipole the distance between the two

poles is negligibly small in comparison to the distance of the observation point.

As a result the potential and ﬁeld vary inversely as the square and cube of the

distance respectively. For bipole ﬁelds, the distance b etween the two charges

is comparable to the distance where we measure the ﬁeld. As a result the

potential an d ﬁeld vary inversely as the ﬁrst and second power of distance.

In this section, we shall develop the expressions for potentials and ﬁelds

for static ﬁeld. Let the charges + q and −q separated by a distance ‘l’ are

placed along the z-axis. ql is the moment of the dipole. The point dipole is

deﬁned as Lim

l→0

q→∞

ql = ﬁnite.

Figure 4.7 shows the location of the dipole. The point of observation P is

located at a certain point x, y, z in a cartesian coordinates. The vector l is

from +q to −q. The potential at P is given by

φ =

4π ∈



−



(4.26)

Substituting the values of r

and r

,weget

φ =

4π ∈

)



− lr cos θ



−1/2

−



+lrcosθ



−1/2

4π ∈

)



−

cos θ



−1/2

−



cos θ



−1/2

(4.27)

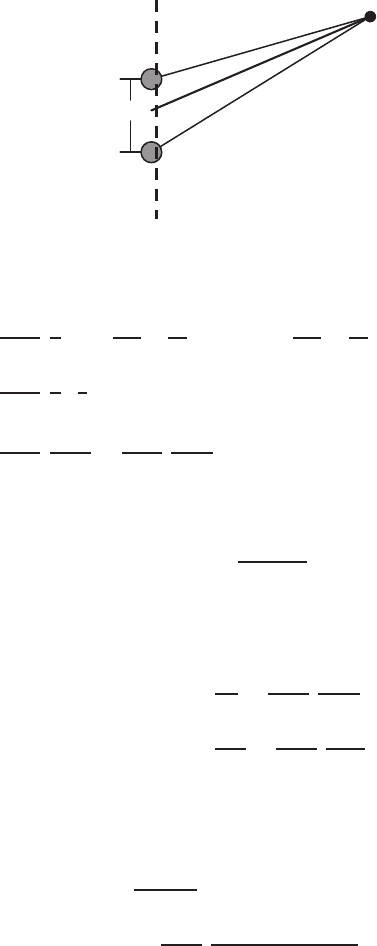
4.8 Field due to an Electrostatic Dipole 83

-q

Fig. 4.7. Shows the electrostatic dipole. P is the measuring point of potential and

ﬁeld

4π ∈



1 −

cos θ −1+

cos θ

+ .... (4.28)

4π ∈



cos θ +1

and higher order terms

4π ∈

cos θ



4π ∈

cos θ

where



P is the dipole moment. (4.29)

The expression for the dipole ﬁeld is,



P.a

4π ∈ .r

. (4.30)

The ﬁeld components in spherical and cartisian coordinates are respectively

given by



= −

∂φ

∂r



4π ∈

cos θ

(4.31)



= −

∂φ

r∂θ



4π ∈

sin θ

(4.32)



=0. (4.33)

The total ﬁeld is



4π ∈ r

(a

2cosθ + a

. sin θ)



4π ∈

)

3/2

. (4.34)

The components are

84 4 Electrostatics



4π ∈

3xz

)

5/2



4π ∈

3xz



4π ∈

3yz

(4.35)



4π ∈



)

5/2

−

)

3/2



4π ∈



−



. (4.36)

For dipoles, the expressions for the potential can also be written as

φ =

4π ∈



−



4π ∈

.ql



−



4π ∈



P.Lim

l→0

∂

∂l





So the diﬀerential form of the expression for potential at a point due to a

dipole is given by

φ =



4π ∈

∂

∂l





. (4.37)

The potential due to a single pole is φ =

4π∈

. For surface distribution of

single poles, the expression for the potential will be

φ =



σds

(4.38)

where σ is the surface density of charge. For dipoles, the direction of the dipole

will be at right angles to the surface. If



P is the moment of the dipole per

unit area,



Pds is the moment of the dipole for a small area ds. Assume that

each dipole is normal to the surface. So the potential at a point p due to the

elementary sur face ds. (Fig. 4.8) is

φ =



Pds

4π ∈

∂

∂n





(4.39)

The total potential due to a surface distribution of dipoles is given by

φ =





Pds

4π ∈

∂

∂n





(4.40)

where the direction of the moment is at right angles to the direction of the

surface. Therefore

4.9 Poisson and Laplace Equations 85

Fig. 4.8. Dipole surface

φ =





4π ∈

ds cos θ



4π ∈



dω =



Pω

4π ∈

(4.41)

where ω is the solid angle subtented at the point P. p is the dipole moment

due to the surface S.

4.9 Poisson and Laplace Equations

Starting from equation (4.25),i.e.

∇D=ρ,

we can write

∇.ε



E=ρ

⇒∇.



∈

. (4.42)

Since

E=−∇φ,

therefore

∇.∇φ = −

∈

⇒∇

φ = −

∈

. (4.43)

This is known as the Poisson’s equation. In a free space where there is no

electrostatic source, (4.43) reduces to,

∇

φ = 0 (4.44)

86 4 Electrostatics

This is a Laplace equation These equatio n s are of primary importance in

scalar potential ﬁeld theory. In r ectangular coo rdinates, Poisson or Laplace

equation is written as,

∂

∂x

∂

∂y

∂

∂z

= −

∈

or 0 (4.45)

depen d in g upon whether the source is inclu ded in or excluded from the vol-

ume.

These are second order partial diﬀerential equations and are related to

the rate of change of potential in three mutually perpendicular directions. In

terms of electric ﬁeld it can b e written as

∇.



∈

or 0. (4.46)

4.10 Electrostatic Energy

A capacitor gets charged when a voltage φ is established between the two

plates. The stored energy can be converted into heat by discharging the cap ac-

itor. The amount of energy stored can be calculated from the work done in

charging the capacitor.

Since the potential is deﬁned as the work done in moving a unit charge

from inﬁnity to a particular point, the work done by moving a small charge ∆q

through the potential diﬀerence of φ is φ∆q. The voltage φ can be expressed

φ =

. (4.47)

The work done in increasing charge in a capacitor by an amount dq is

dq. (4.48)

The total work done in charging the capacitor to q Coulomb is

Total work =



dq =

. (4.49)

Stored energy in a charged capacitor is

φq =

C. (4.50)

Since



i.e., the potential per unit length and ∈= C

,wegettheexpres-

sion of the electrostatic stored energy as

C =

. ∈ .

∈ E

. (4.51)

So the stored electrostatic energy per unit volume is

∈ E

. (4.52)

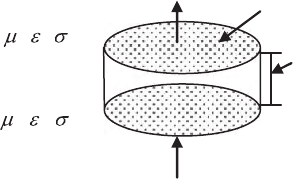
4.11 Boundary Conditions 87

4.11 Boundary Conditions

The normal component of



Dis





D.n.ds.

Applying Gauss’s divergence theorem, we get





D.n.ds =



div



D.dv =



ρdv = q (4.53)

Here q is the total charge and ρ is the volume density of charge. Let us assume

an elementary thin cylinder with negligible thickness w i th two faces on two

sides of the boundary (Fig. 4.9). The normal component of the displacement

vectors will go out of this volume for normal induction. Therefore Dn

and Dn

will be in the opposite direction. From Gauss’s law of total normal induction

we can write

)∆a = w∆a (4.54)

where D

and D

are the displacement vectors, n

and n

are the normal

vectors from the bottom and top surfaces of the cylinder, ∆a is the surface

area of the cylinder and w is the surface density of charge. Since q =



ρdv =

ρ∆l.∆a (where ρ is the volume density of charge), we get

w=ρ∆l,

and

− D

).n = w (4.55)

This equation shows that normal component D

of the vector



D is discontinu-

ous at an interface due to accumulation of surface charge of density w. On the

surface of a conductor, surface charge density dissipates quickly but on a sur-

face of an insulator accumulated charge does not dissipate so quickly. Hence

111

222

Fig. 4.9. Normal component of the displacement vector at the boundary between

the two media of diﬀerent electrical permittivity

88 4 Electrostatics

across the interface involving all except the poorest conductors or dielectrics,

the normal component of



D is continuous across the boundary i.e.,

=Dn

(4.56)

Since the electrostatic potential is also continuous across the boundary.

The boundary conditions generally applied to solve an electrostatic problem

are

(i) φ

= φ

(ii) ∈



∂φ

∂n



= ∈



∂φ

∂n



. (4.57)

4.12 Basic Equations in Electrostatic Field



F =

4π ∈

Coulomb

′

slaw (4.58)



F=q



E (4.59)



E =

4π ∈

.r (4.60)



E =Lim

∆q→o

∆F

∆q

(4.61)

div



E =

∈

where q

is the volume density of charge. or

∇

E =

∈

Poisson’s equation (4.62)



E=−gradφ

. φ

is the scalar potential in electrostatics (4.63)

7. ∇



E = O Laplace equation is a source free region (4.64)



D = ∈



E (4.65)

9. div



D=ρ (4.66)