Richards J.A., Jia X. Remote Sensing Digital Image Analysis: An Introduction
Подождите немного. Документ загружается.

Appendix C
Binary Representation of Decimal Numbers
In digital data handling we frequently refer to numbers in binary form; this is because
computers and their associated storage media represent data in this format. In the
binary system the numbers are arranged in columns that represent powers of 2 while
in the decimal system numbers are arranged in columns that are powers of 10. Thus
whereas we can count up to 9 in each column in the decimal system we can only count
up to one in each binary column. From the right, the columns represent 2
0
, 2
1
, 2
2
etc., so that the decimal numbers between 0 and 7 have the binary versions:
Decimal Binary
2
2
2
1
2
0
0 000
1 001
2 010
3 0 1 1 (i.e. 2 +1)
4 100
5 1 0 1 (i.e. 4 + 1)
6 1 1 0 (i.e. 4 + 2)
7 1 1 1 (i.e. 4 + 2 +1)
The digits in the binary system are referred to as bits. In the above example it can be
seen that by using just 3 binary digits it is not possible to represent decimal numbers
beyond 7 – i.e. a total of 8 decimal numbers altogether, including 0. To represents 16
decimal numbers, which could be 16 levels of brightness in remote sensing image
data between 0 and 15, it is necessary to have a binary “word” with 4 bits. In that
case the word 1111 is equivalent to decimal 15. In this way it is readily shown that
the numbers of decimal values that can be represented by various numbers of binary
digits are:
416 C Binary Representation of Decimal Numbers
Number of bits Number of decimal levels
1 2 (i.e. 0,1)
2 4 (0, 1, 2, 3,)
3 8 (0, ...,7)
4 16 (0, ..., 15)
5 32 etc.
664
7 128
8 256
9 512
10 1024
11 2048
12 4096
An eight bit word, which can represent 256 decimal numbers between 0 and 255,
is referred to as a byte and is a fundamental data unit used in computers.
Appendix D
Essential Results from Vector and Matrix Algebra
D.1
Definition of a Vector and a Matrix
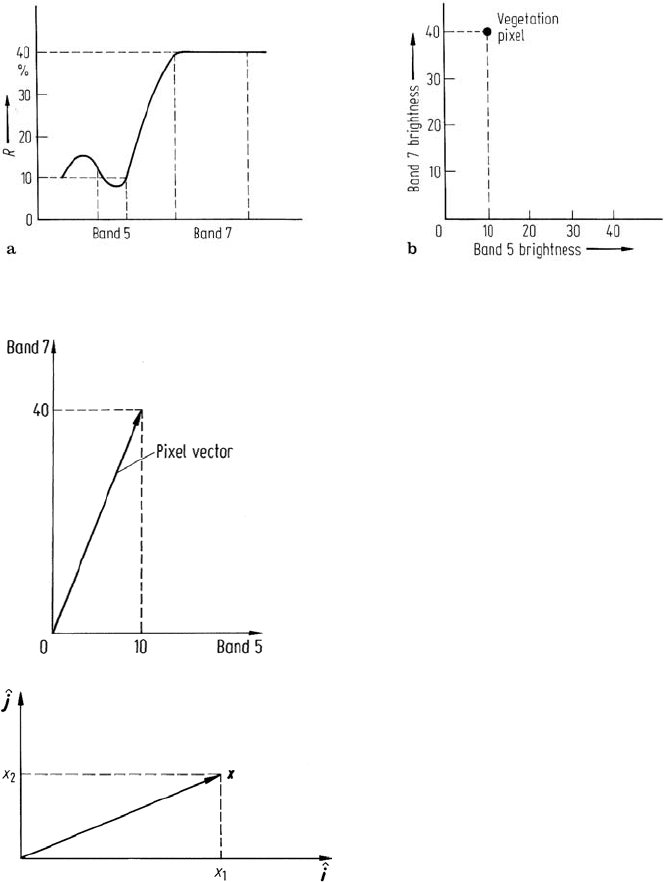
The pixels in an image can be plotted in a rectangular co-ordinate system according
to their brightness values in each band. For example, for Landsat MSS bands 5 and 7
a vegetation pixel would appear somewhat as shown in Fig. D.1. The pixel can be
described by its co-ordinates (10, 40); this will be a set of four numbers if all 4 MSS
bands are considered, in which case the co-ordinate system also is four dimensional.
For the rest of this discussion only two dimensions will be used for illustration but the
results apply to any number. For example a 7 dimensional space would be required
for Landsat ETM+ data. The vector space will have several hundred dimensions for
imaging spectrometer data.
An alternative but equivalent means by which the pixel point can be represented
is as a vector drawn from the origin, as illustrated in Fig. D.2. In this context the
vector is simply an arrow that points to the pixel. While we never actually draw the
vector as such it is useful to remember that it is implied in much of what follows.
Mathematically a vector from the origin is described in the following way. First
we define so-called unit vectors along the co-ordinate directions. These are simply
direction indicators, which for the two dimensional case are as shown in Fig. D.3.
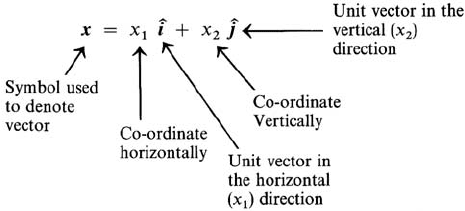
With these, the vector is written as
418 D Essential Results from Vector and Matrix Algebra
Fig. D.1. a Spectral reflectance characteristic of vegetation; b typical vegetation pixel plotted
in a rectangular co-ordinate system
Fig. D.2. Representation of a pixel point in multi-
spectral space by a vector drawn from the origin
Fig. D.3. Definition of unit vectors
In “shorthand” form we represent the vector as
x =
x
1
x
2
which is properly referred to as a column vector, owing to its vertical arrangement.
Note that the unit vectors, and thus the corresponding co-ordinate directions are
D.2 Properties of Matrices 419
implied by the ordering in the column. Sometimes a row version is used. This is
called the transpose of x and is written as
x
t
=[x
1
x
2
].
Recall that for Landsat MSS data x will have 4 column entries representing the four
response values for the pixel that x describes.
Sometimes we might wish to create another vector y from an existing vector x.
For illustration, if we take both to be just two dimensional then the components of y
can be obtained most generally according to the pair of equations
y
1
= m
11
x
1
+ m
12
x
2
y
2
= m
21
x
1
+ m
22
x
2
i.e. the components of y are just (linear) combinations of those of x. In shorthand
this transformation of the vector is expressed as
y
1
y
2
=
m
11
m
12
m
21
m
22
x
1
x
2
or
y = Mx
where M is referred to as a matrix of coefficients. By comparing the previous ex-
pressions, note how a multiplication of a matrix by a vector is carried out.
D.2
Properties of Matrices
The inverse of M is called M
−1
and is defined by
MM
−1
= I
where I is the identity matrix
⎡
⎢
⎢
⎢
⎣
10
01
.
.
.
1
⎤
⎥
⎥
⎥
⎦
which, if used to transform the vector x, will leave it unchanged. This can be seen if
it is used in place of M in the equations above. The inverse of a matrix is not always
easily computed. It should be noted however that it can be expressed as
M
−1
= M
∗
/|M|
where M
∗
is called the adjoint of M and |M|is called its determinant. The adjoint, in
theory, is a transposed matrix of cofactors. This is not important in general for remote
sensing since all the calculations are usually performed with software that includes
420 D Essential Results from Vector and Matrix Algebra
a procedure for inverting a matrix. However it is useful for illustration purposes to
know that the adjoint for a 2 × 2 matrix is:
M
∗
=
m
22
−m
12
−m
21
m
11
when M =
m
11
m
12
m
21
m
22
Similarly large order determinant calculations are carried out by computer. It is only
necessary to note, for illustration, that
m
11
m
12
m
21
m
22
= m
11
m
22
− m
21
m
12
= a scalar constant.
D.3
Multiplication, Addition and Subtraction of Matrices
If M and N are two matrices, chosen as 2 ×2 for illustration and defined as
M =
m
11
m
12
m
21
m
22
N =
n
11
n
12
n
21
n
22
then
M ± N =
m
11
± n
11
m
12
± n
12
m
21
± n
21
m
22
± n
22
and
MN =
m
11
m
12
m
21
m
22
×
n
11
n
12
n
21
n
22
=
m
11
n
11
+ m
12
n
21
m
11
n
12
+ m
12
n
22
m
21
n
11
+ m
22
n
21
m
21
n
12
+ m
22
n
22
Note that the last expression is obtained by multiplying, term by term, the rows of
the first matrix by the columns of the second. Within each multiplication the terms
are summed. This pattern holds for larger matrices.
Division is not defined as a matrix operation. Rather its place is taken by the
definition of a matrix inverse, as in the above section.
D.4
The Eigenvalues and Eigenvectors of a Matrix
We have discussed the matrix M above as a matrix that transforms one vector to
another, (alternatively it can be used to transform the co-ordinate system in which
a point or vector is described). It is relevant at this stage to ask if there is a vector
that can be multiplied by a simple (but in general complex) number and thus be
transformed in exactly the same manner as it would be had it been multiplied by
the matrix M. In other words can we find a vector x in our co-ordinate space and a
(complex) number λ such that
D.6 An Orthogonal Matrix – The Concept of Matrix Transpose 421
Mx = λx (i.e. y = λx is equivalent to y = Mx).
This implies
Mx − λx = 0
or
(M − λI )x = 0 (D.1)
The theory of simultaneous equations tells us that for this equation to be true it is
necessary to have either x = 0or
|M − λI |=0 (D.2)
This expression is a polynominal equation in λ. When evaluated it yields values for λ.
When these are substituted into (D.l) the vectors x corresponding to those λ will be
found. Those λ’s are called the eigenvalues of M and the associated x’s are called
the eigenvectors.
D.5
Some Important Matrix, Vector Operations
If x is a column vector, say x =
x
1
x
2
then
xx
t
=
x
1
x
2
[x
1
x
2
]
=
⎡
⎣
x
2
1
x
1
x
2
x
1
x
2
x
2
2
⎤
⎦
i.e. a matrix
and
x
t
x =[x
1
x
2
]
x
1
x
2
= x
2
1
+ x
2
2
i.e. a constant (this is often referred to as the dot product, scalar product
or inner product).
D.6
An Orthogonal Matrix – The Concept of Matrix Transpose
The inverse of an orthogonal matrix is identical to its transpose. Thus, if M is
orthogonal then
422 D Essential Results from Vector and Matrix Algebra
M
−1
= M
t
and M
t
M = I,
where M
t
is the transpose of the matrix, given by rotating all the elements about the
principal diagonal (that which runs through the elements m
11
,m
22
,m
33
,...).
D.7
Diagonalisation of a Matrix
Consider a transformation matrix M such that
y = Mx.
As before the eigenvalues λ
i
of M and their associated eigenvectors x
i
are defined
by the expression
λ
i
x
i
= Mx
i
,i= 1,...n
where n is the number of distinct eigenvalues.
These n different equations can be expressed in the compact manner
X = MX
where is the diagonal matrix
⎡
⎢
⎣
λ
1
0
.
.
.
0 λ
n
⎤
⎥
⎦
and X is the matrix of eigenvectors (x
1
, x
2
,...x
n
).
Consequently = X
−1
MX
If X is orthogonal then X
−1
= X
t
so that = X
t
MX.
Appendix E
Some Fundamental Material
from Probability and Statistics
E.1
Conditional Probability
It is the purpose of this Appendix to outline some of the fundamental statistical con-
cepts commonly used in remote sensing theoretical developments. Remote sensing
terminology is used throughout and an emphasis is placed on understanding rather
than theoretical rigour.
The expression p(x) is interpreted as the probability that the event x occurs. In
the case of remote sensing, if x is a pixel vector, p(x) is the probability that a pixel
can be found at position x in multispectral space.
Often we wish to know the probability of an event occuring conditional upon
some other event or circumstance. This is written as p(x|y) which is expressed as
the probability that x occurs given that y is specified. As an illustration p(x|ω
i
) is
the probability of finding a pixel at position x in multispectral space, given that we
are interested in class ω
i
– i.e. it is the probability that a pixel from class ω
i
exists at
position x. These p(x|y) are referred to as conditional probabilities; the available y
generally form a complete set. In the case of remote sensing the set of ω
i
,i = 1,...M
are the complete set of spectral classes used to describe the image data for a particular
exercise. If we know the complete set of p(x|ω
i
) – which are often referred to as
the class conditional probabilities – then we can determine p(x) in the following
manner. Consider the product p(x|ω)p(ω
i
) where p(ω
i
) is the probability that class
ω
i
occurs in the image (or that a pixel selected at random will come from class ω
i
).
The product is the probability that a pixel at position x in multispectral space is an ω
i
pixel. The probability that a pixel from any class can be found at position x clearly
is the sum of the probabilities that pixels will be found there from all the available
classes. In other words
p(x) =
M
i=1
p(x|ω
i
)p(ω
i
) (E.1)

424 E Some Fundamental Material from Probability and Statistics
The product p(x|ω
i
)p(ω
i
) is called the joint probability of the “events” x and ω
i
.
It is interpreted strictly as the probability that a pixel occurs at position x and that
the class is ω
i
(this is different from the probability that a pixel occurs at position x
given that we are interested in class ω
i
. The joint probability is written
p(x,ω
i
) = p(x|ω
i
)p(ω
i
) (E.2a)
We can also write
p(ω
i
, x) = p(ω
i
|x)p(x) (E.2b)
where p(ω
i
|x) is the conditional probability that expresses the likelihood that the
class is ω
i
given that we are examining a pixel at position x in multispectral space.
Often this is called the posterior probability of class ω
i
. Again p(ω
i
, x) is the prob-
ability that ω
i
and x exist together, which is the same as p(x,ω
i
). As a consequence,
from (E.2a) and (E.2b)
p(ω
i
|x) = p(x|ω
i
)p(ω
i
)/p(x) (E.3)
which is known as Bayes’ theorem (Freund, 1992).
E.2
The Normal Probability Distribution
E.2.1
The Univariate Case
The class conditional probabilities p(x|ω
i
) in remote sensing are frequently assumed
to belong to a normal probability distribution. In the case of a one dimensional spectral
space this is described by
p(x|ω
i
) = (2π)
−1/2
σ
−1
i
exp
#
−
1
2
(x − m
i
)
2
/σ
2
i
$
(E.4)
in which x is the single spectral variable, m
i
is the mean value of x and σ
i
is its
standard deviation; the square of the standard deviation, σ
2
i
, is called the variance of
the distribution. The mean is referred to also as the expected value of x since, on the
average, it is the value of x that will be observed on many trials. It is computed as the
mean value of a large number of samples of x. The variance of the normal distribution
is found as the expected value of the difference squared of x from its mean. A simple
average of this squared difference gives a biased estimate. An unbiased estimate is
obtained from (Freund, 1992)
σ
2
i
=
1
q
i
− 1
q
i
j=1
(x
j
− m
i
)
2
(E.5)
where q
i
is the number of pixels in class ω
i
and x
j
is the jth sample.
