Richards J.A., Jia X. Remote Sensing Digital Image Analysis: An Introduction

Подождите немного. Документ загружается.

4.6 Density Slicing 101

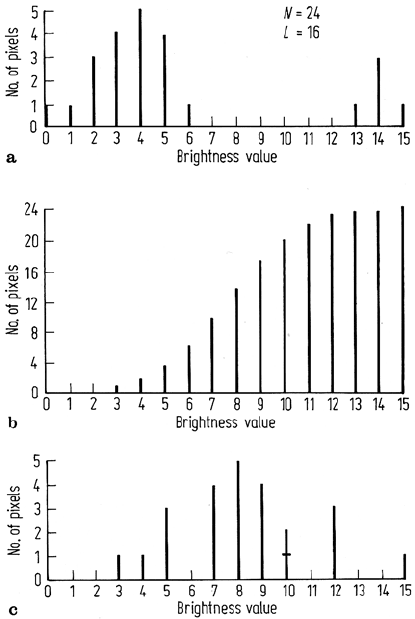
Fig. 4.15. Illustration of the modiﬁcation of an image histogram to a pseudo-Gaussian shape.

a Original histogram; b Cumulative normal histogram; c Histogram matched to Gaussian

reference

usually at the mid-point of the brightness scale and commonly the standard deviation

is chosen such that the extreme black and white regions are three standard deviations

from the mean. A simple illustration is shown in Fig. 4.15.

4.6

Density Slicing

4.6.1

Black and White Density Slicing

A point operation often performed with remote sensing image data is to map ranges

of brightness value to particular shades of grey. In this way the overall discrete

number of brightness values used in the image is reduced and some detail is lost.

However the effect of noise can also be reduced and the image becomes segmented,

102 4 Radiometric Enhancement Techniques

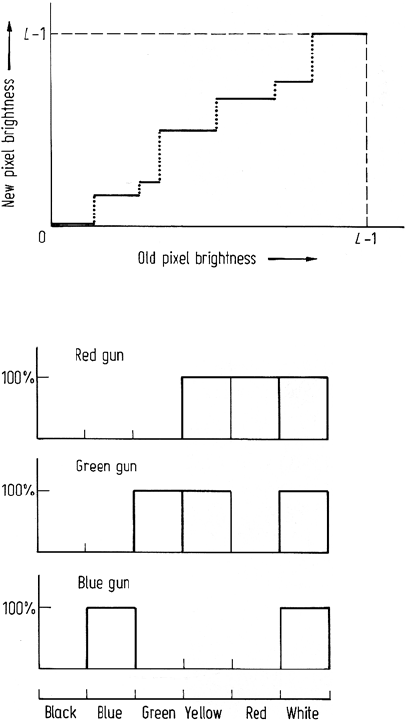
Fig. 4.16. The brightness value

mapping function corresponding

to black and white density

slicing. The thresholds are user

speciﬁed

Fig. 4.17. Simple example of creating the

look-up tables for a colour display device

to implement colour density slicing. Here

only six colours have been chosen for sim-

plicity

or sometimes contoured, in sections of similar grey level, in which each segment is

represented by a user speciﬁed brightness. The technique is known as density slicing

and ﬁnds value, for example, in highlighting bathymetry in images of water regions

when penetration is acceptable. When used generally to segment a scalar image into

signiﬁcant regions of interest it is acting as a simple one dimensional parallelepiped

classiﬁer (see Sect. 8.4). The brightness value mapping function for density slicing

is as illustrated in Fig. 4.16. The thresholds in such a function are entered by the user.

An image in which the technique has been used to highlight bathymetry is shown

in Fig. 4.18. Here differences in Landsat multispectral scanner visible imagery, at

brightnesses too low to be discriminated by eye, have been mapped to new grey levels

to make the detail apparent.

4.6 Density Slicing 103

Fig. 4.18. Illustration of contouring in water detail using density slicing. a The image used is

a band 5 + band 7 composite Landsat multispectral scanner image, smoothed to reduce line

striping and then density sliced; b Black and white density slicing; c Colour density slicing

104 4 Radiometric Enhancement Techniques

4.6.2

Colour Density Slicing and Pseudocolouring

A simple yet lucid extension of black and white density slicing is to use colours to

highlight brightness value ranges, rather than simple grey levels. This is known as

colour density slicing. Provided the colours are chosen suitably, it can allow ﬁne detail

to be made immediately apparent. It is a particularly simple operation to implement

on a display system by establishing three brightness value mapping functions in the

manner depicted in Fig. 4.17. Here one function is applied to each of the colour

primaries used in the display device. An example of the use of colour density slicing,

again for bathymetric purposes, is given in Fig. 4.18.

This technique is also used to give a colour rendition to black and white imagery.

It is then usually called pseudocolouring. Where possible this uses as many distinct

hues as there are brightness values in the image. In this way the contours introduced

by density slicing are avoided. Moreover it is of value in perception if the hues used

are graded continuously. For example, starting with black, moving from dark blue,

mid blue, light blue, dark green, etc. through to oranges and reds will give a much

more acceptable pseudocoloured product than one in which the hues are chosen

arbitarily.

References for Chapter 4

Much of the material on contrast enhancement and contrast matching treated in this chapter will

be found also in Castleman (1996) and Gonzalez and Woods (1992) but in more mathematical

detail. Passing coverages are also given by Moik (1980) and Hord (1982). More comprehensive

treatments will be found in Schowengerdt (1997), Jensen (1986), Mather (1987) and Harrison

and Jupp (1990).

The papers by A. Schwartz (1976) and J.M. Soha et al. (1976) give examples of the

effect of histogram equalization and of Gaussian contrast stretching. Chavez et al. (1979) have

demonstrated the performance of multicycle contrast enhancement, in which the brightness

value mapping function y = f(x)is cyclic. Here, several sub-ranges of input brightness value

x are each mapped to the full range of output brightness value y. While this destroys the

radiometric calibration of an image it can be of value in enhancing structural detail.

K.R. Castleman, 1996: Digital Image Processing, 2e, N.J., Prentice-Hall.

P.S. Chavez, G.L. Berlin, and W.B. Mitchell, 1979: Computer Enhancement Techniques of

Landsat MSS Digital Images for Land Use/Land Cover Assessment. Private Communi-

cation, US Geological Survey, Flagstaff, Arizona.

R.C. Gonzalez and R.E. Woods, 1992: Digital Image Processing, Mass., Addison-Wesley.

B.A. Harrison and D.L.B. Jupp, 1990: Introduction to Image Processing, Canberra, CSIRO.

A. Hogan, 1981: A Piecewise Linear Contrast Stretch Algorithm Suitable for Batch Landsat

Image Processing. Proc. 2nd Australasian Conf. on Remote Sensing, Canberra, 6.4.1–

6.4.4.

R.M. Hord, 1982: Digital Image Processing of Remotely Sensed Data, N.Y., Academic.

J.R. Jensen, 1986: Introductory Digital Image Processing — a Remote Sensing Perspective.

N.J., Prentice-Hall.

Problems 105

P.M. Mather, 1987: Computer Processing of Remotely-Sensed Images. Suffolk, Wiley.

J.G. Moik, 1980: Digital Processing of Remotely Sensed Images, Washington, NASA.

A. Schwartz, 1976: New Techniques for Digital Image Enhancement, in Proc. Caltech/JPL

Conf. on Image Processing Technology, Data Sources and Software for Commercial and

Scientiﬁc Applications, California, Nov. 3–5, 2.1–2.12.

R.A. Schowengerdt, 1997: Remote Sensing Models and Methods for Image Processing, 2e,

New York, Academic.

J.M. Soha, A.R. Gillespie, M.J. Abrams and D.P. Madura, 1976: Computer Techniques for

Geological Applications; in Proc. Caltech/JPL Conf. on Image Processing Technology,

Data Sources and Software for Commercial and Scientiﬁc Applications, Nov. 3–5, 4.1–

4.21.

Problems

4.1 One form of histogram modiﬁcation is to match the histogram of an image to a Gaussian

or normal function. Suppose a raw image has the histogram indicated in Fig. 4.19. Produce

the look-up table that describes how the brightness values of the image should be changed if

the histogram is to be mapped, as nearly as possible, to a Gaussian histogram with a mean of

8 and a standard deviation of 2 brightness values. Note that the sum of counts in the Gaussian

reference histogram must be the same as that in the raw data histogram.

Fig. 4.19. Histogram

4.2 The histogram of a particular image is shown in Fig. 4.20. Produce the modiﬁed version

that results from:

Fig. 4.20. Histogram of a single dimensional image

106 4 Radiometric Enhancement Techniques

(i) a simple linear contrast stretch which makes use of the full range of brightness values

(ii) a simple piecewise linear stretch that maps the range (12, 23) to (0, 31) and

(iii) histogram equalization (i.e. producing a quasi-uniform histogram).

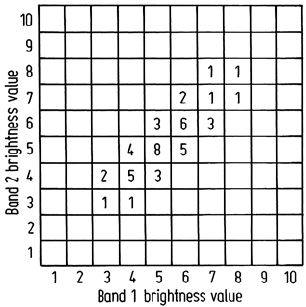
4.3 A two-dimensional histogram for particular two band image data is shown in Fig. 4.21.

Determine the histogram that results from a simple linear contrast stretch on each band indi-

vidually.

Fig. 4.21. Two-dimensional histogram

4.4 Determine, algebraically, the contrast mapping function that equalizes the contrast of an

image which has a Gaussian histogram at the centre of the brightness value range, with the

extremities of the range being three standard deviations from the mean.

4.5 What is the shape of the cumulative histogram of an image that has been contrast (his-

togram) equalized? Can this be used as a ﬁgure of merit in histogram equalization?

4.6 Clouds and large regions of clear, deep water frequently give histograms for near infrared

imagery that have large high brightness level or low brightness value bars respectively. Sketch

histograms of these types. Qualitatively, equalize the histograms using the material of Sect. 4.4

and comment on the undesirable appearance of the corresponding contrast enhanced images.

Show that the situation can be rectiﬁed somewhat by artiﬁcially limiting the large bars to values

not greatly different to the heights of other bars in the histogram, provided the accompanying

cumulative histograms are normalised to correspond to the correct number of pixels in the

image. A similar, but more effective procedure has been given in A. Hogan (1981).

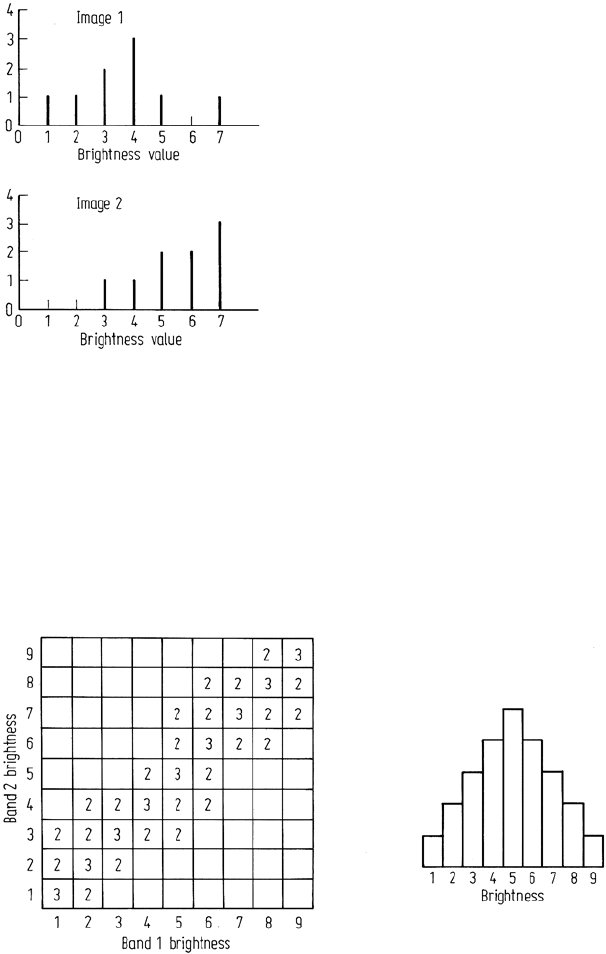
4.7 Two Landsat images are to be joined side by side to form a mosaic for a particular

application. To give the new, combined image a uniform appearance it is decided that the

range and distribution of brightness levels in the ﬁrst image should be made to match those of

the second image, before they are joined. This is to be carried out by matching the histogram

of image 1 to that of image 2. The original histograms are shown in Fig. 4.22. Produce a look

up table that can be used to transform the pixel brightness values of image 1 in order to match

the histograms as nearly as possible. Use the look-up table to modify the histogram of image 1

and comment on the degree to which contrast matching has been achieved.

Problems 107

Fig. 4.22. Histograms of image 1 and image 2

4.8 (a) Contrast enhancement is frequently carried out on remote sensing image data. Describe

the advantages in doing so, if the data is to be analysed by

(i) photointerpretation

(ii) quantitative computer methods.

(b) A particular two band image has the two dimensional histogram shown in Fig. 4.23. It is

proposed to enhance the contrast of the image by matching the histograms in each band to

the triangular proﬁle shown. Produce look-up tables to enable each band to be enhanced, and

from these produce the new two-dimensional histogram for the image.

Fig. 4.23. Two dimensional histogram

108 4 Radiometric Enhancement Techniques

4.9 Plot the equilized histogram for the example of Table 4.2. Compare it with Fig. 4.9 and

comment on the effect of restricting the range of output brightnesses. Repeat the exercise for

the cases of 4 and 2 output brightness values.

4.10 Suppose a particular image has been modiﬁed by (i) linear contrast enhancement and

(ii) by histogram equalisation. Suppose you have available the digital image data for both

the original image and the contrast modiﬁed versions. By inspecting the data (or histograms)

describe how you would determine quantitatively which technique was used in each case.

Geometric Enhancement

Using Image Domain Techniques

5.1

Neighbourhood Operations

This chapter presents methods by which the geometric detail in an image may be

modiﬁed and enhanced. The speciﬁc techniques covered are applied to the image data

directly and could be called image domain techniques. These are alternatives to pro-

cedures used in the spatial frequency domain which require Fourier transformation

of the image beforehand. Those are treated in Chap. 7.

In contrast to the point operations used for radiometric enhancement, techniques

for geometric enhancement are characterised by operations over neighbourhoods.

The procedures still determine modiﬁed brightness values for an image’s pixels;

however, the new value for a given pixel is derived from the brightnesses of a set of the

surrounding pixels. It is this spatial interdependence of the pixel values that leads to

variations in the perceived image geometric detail. The neighbourhood inﬂuence will

be apparent readily in the techniques of this chapter; for the Fourier transformation

methods of Chap. 7 it will be discerned in the deﬁnition of the Fourier operation.

5.2

Template Operators

Geometric enhancements of most interest in remote sensing generally relate to

smoothing, edge detection and enhancement, and line detection. Enhancement of

edges and lines leads to image sharpening. Each of these operations is considered in

the following sections. Most of the methods to be presented are, or can be expressed

as, template techniques in which a template, box or window is deﬁned and then

moved over the image row by row and column by column. The products of the pixel

brightness values, covered by the template at a particular position, and the template

entries, are taken and summed to give the template response. This response is then

used to deﬁne a new brightness value for the pixel currently at the centre of the

template. When this is done for every pixel in the image, a radiometrically modiﬁed

110 5 Geometric Enhancement Using Image Domain Techniques

Fig. 5.1. A3× 3 template positioned over a group of nine image pixels, showing the relative

locations of pixels and template entry addresses

image is produced that enhances or smooths geometric features according to the

speciﬁc numbers loaded into the template. A 3 ×3 template is illustrated in Fig. 5.1.

Templates of any size can be deﬁned, and for an M by N pixel sized template, the

response for image pixel i, j is

r(i,j) =



m=1



n=1

φ(m, n) t (m, n) (5.1)

where φ(m, n) is the pixel brightness value, addressed according to the template

position and t (m, n) is the template entry at that location. Often the template entries

collectively are referred to as the ‘kernel’ of the template and the template technique

generally is called convolution, in view of its similarity to time domain convolution

in linear system theory. This concept is developed in Sect. 5.3 below.

5.3

Geometric Enhancement as a Convolution Operation

This section presents a brief linear system theory basis for the use of the template

expression of (5.1). It contains no results essential to the remainder of the chapter

and can be safely passed over by the reader satisﬁed with (5.1) from an intuitive

viewpoint.

Consider a signal in time represented as x(t). Suppose this is passed through a

system of some sort to produce a modiﬁed signal y(t) as depicted in Fig. 5.2. The

system here could be an intentional one such as an ampliﬁer or ﬁlter, inserted to

change the signal in a predetermined way; alternatively it could represent uninten-

tional modiﬁcation of the signal such as by distortion or the effect of noise. The

properties of the system can be described by a function of time h(t). This is called

Fig. 5.2. Signal model of a linear system