Richard S. Gallagher. Computer Visualization: Graphics Techniques for Engineering and Scientific Analysis

Подождите немного. Документ загружается.

Previous Table of Contents Next

reserved. Reproduction whole or in part in any form or medium without express written permission of

EarthWeb is prohibited. Read EarthWeb's privacy statement.

Search Tips

Advanced Search

Computer Visualization: Graphics Techniques for Engineering and Scientific Analysis

by Richard S. Gallagher. Solomon Press

CRC Press, CRC Press LLC

ISBN: 0849390508 Pub Date: 12/22/94

Search this book:

Previous Table of Contents Next

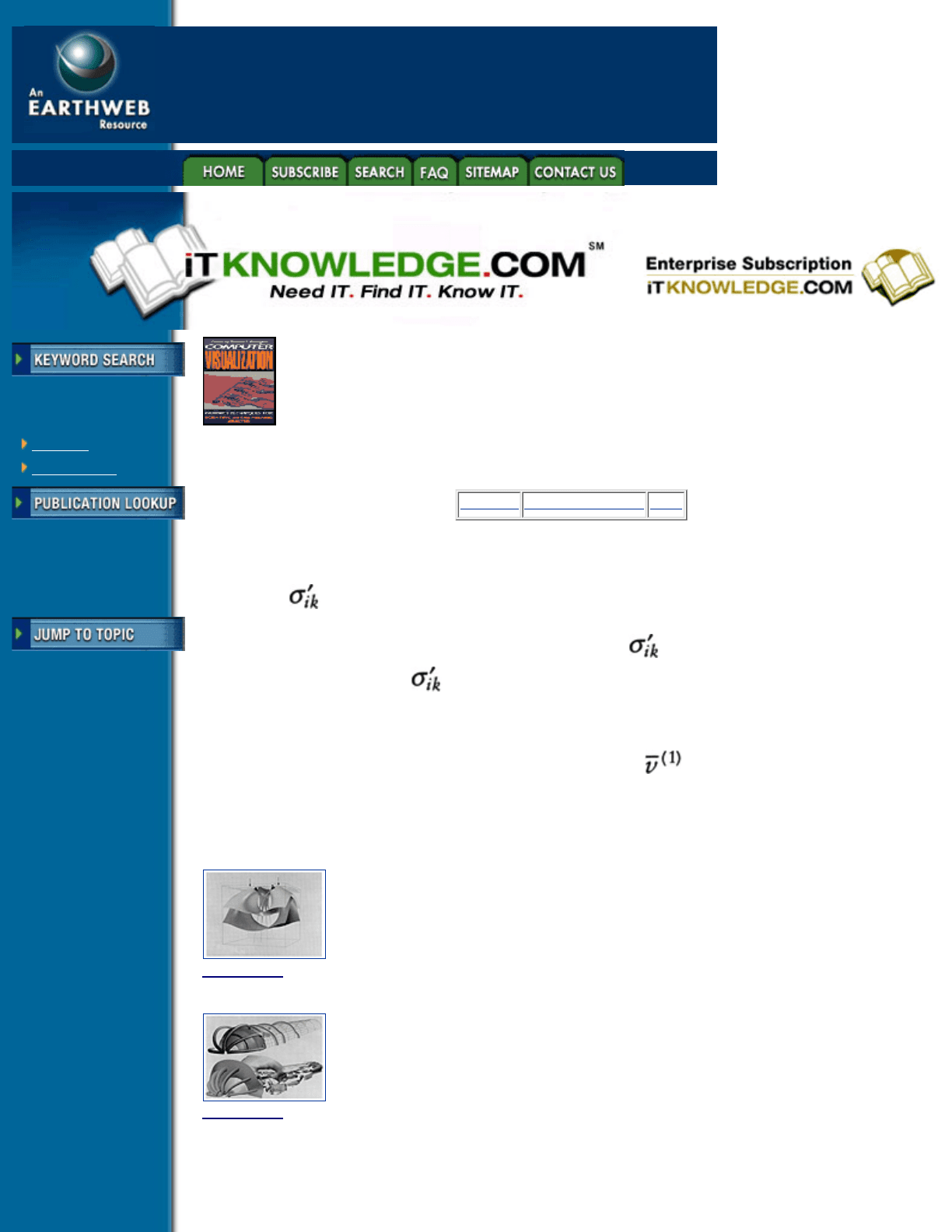
We can modify the coloring scheme of hyperstreamlines to represent other aspects of the data. For example,

we can color a tube in function of the angle between the radial vector

in the plane of the tube’s

cross-section and the force

acting on a facet with normal . Color therefore discriminates among

tensile, compressive, and pure shear transverse directions [9].

Reversible momentum flux density. A specific example of flow data illustrates how hyperstreamlines may be

used to correlate several different physical quantities. For the reversible part of the momentum flux density

tensor,

in Table 5.2 (see page 152) one may correlate pressure p, velocity direction , and kinetic

energy density k. Indeed, the major eigenvalue of

, and the corresponding unit

eigenvector is the velocity direction. The other eigenvalues are degenerate (»

(2)

= »

(3)

= p) in the whole space.

It follows that only major tubes can be used. Tube trajectories are everywhere tangent to the velocity direction

and are therefore streamlines of the velocity field. Cross-sections are circular, with a diameter proportional to

the pressure. In addition, the color of the tubes is chosen as

so as to represent the kinetic energy density k. Thus, the trajectory, diameter, and color of the major tubes

encode the velocity direction, pressure and kinetic energy density, respectively.

Figure 5.21 Four different stages of a minor tube in an elastic stress tensor field. (From Delmarcelle and

Figure 5.22 shows

in the flow past a hemisphere cylinder. The direction of the incoming flow is 5° to

the left of the hemisphere axis. The detachment at the end of the cylinder is clearly visible. The pattern of

Title

-----------

hyperstreamlines indicates that the momentum is transferred fairly uniformly from the tip of the body to the

end with a globally decreasing kinetic energy shown by color variations. However, there is a region on the

front side of the body where direction, color, and diameter of the first five tubes vary suddenly. These

variations indicate correlated changes in velocity direction, kinetic energy density, and pressure, respectively.

5.4.2 Global Icons

Global icons of vector fields, such as vector field topology and vortex cores, display the collective behavior of

a large set of streamlines. By analogy, global icons of tensor data are obtained by encoding the behavior of a

large number of hyperstreamlines.

Consider the collection

of hyperstreamlines propagating along the eigenvector field given by

Equation 5.10. Important features exist in both the trajectory and the cross-section of these hyperstreamlines.

For example, the locus

is the set of the critical points in the trajectory of the hyperstreamlines . (Here, we use “critical points”

literally. They are points where the magnitude of the longitudinal eigenvector field

vanishes. We do not

presuppose any specific pattern of the neighboring hyperstreamlines.) Further, the surface

where »

(i)

and »

(k)

are the transverse eigenvalues, is the locus of points where the cross-section of the

hyperstreamlines

is singular; i.e., reduced to a straight line or a point. In general, surfaces of constant

eccentricity are loci where the cross-section of each hyperstreamline in

has the same shape,

regardless of its orientation and scaling. In particular, the locus

is the set of points where the cross-section degenerates into a circle (zero eccentricity). We refer the reader to

Reference [84] for a detailed discussion of the topology of tensor fields.

Figure 5.22 Reversible momentum flux density tensor in the flow past a hemisphere cylinder. Color scale is

section plate 5.22.)

A global icon of the stress tensor of Figures 5.19 and 5.20 is given in Figure 5.23. The yellow surface is the

locus of critical points of the medium eigenvector

and the green surface represents the critical points of

the major eigenvector

. On both of these surfaces, the cross-section of each minor tube—four of them

are shown—reduces to a straight line. On the blue surface, the transverse eigenvalues are opposite to each

other, and the cross-section is circular. Below the yellow surface, both transverse eigenvalues are positive and

every transverse direction in the cross-section of the minor tubes is in tension. Above the yellow surface, the

medium eigenvalue becomes negative and some transverse directions are in tension while others are

compressive. Inside the green surface, however, every transverse direction is in compression.

Previous Table of Contents Next

reserved. Reproduction whole or in part in any form or medium without express written permission of

EarthWeb is prohibited. Read EarthWeb's privacy statement.

Search Tips

Advanced Search

Computer Visualization: Graphics Techniques for Engineering and Scientific Analysis

by Richard S. Gallagher. Solomon Press

CRC Press, CRC Press LLC

ISBN: 0849390508 Pub Date: 12/22/94

Search this book:

Previous Table of Contents Next

Stresses and viscous stresses. The former concepts are applied to visualize the stress tensor Ãik and viscous

stress tensor

in the flow past a hemisphere cylinder. As shown in Table 5.2 (see page 152), these two

tensors differ only by an isotropic pressure component, implying that their unit eigenvectors are identical.

However, the eigenvalues of Ã

are equal to the eigenvalues of minus a large pressure component. Table

5.2 also shows that visualizing

is equivalent to visualizing the rate-of-strain tensor e

in incompressible

flows.

Hyperstreamlines of the stress tensor are shown in Figure 5.24 (top) (the flow is the same as in Figure 5.22).

The major tubes in front are along the least compressive direction

. Their trajectory show how forces

propagate from the region in front of the cylinder to the surface of the body. The cross-section of the tubes is

very circular, indicating, as expected, that the pressure component of the stresses is dominant. However, the

viscous stresses close to the body create a slightly anisotropic cross-section. On the yellow surface, for

example, the eccentricity is equal to 10%.

Figure 5.23 Global icon of the stress tensor of Figures 5.19 and 5.20. (Frorr Delmarcelle and Hesselink,

Figure 5.24 Stress tensor (top) and viscous stress tensor (bottom) in the flow past a hemisphere cylinder.

The helices are along the medium eigenvector field. They propagate mainly parallel to the cylinder surface,

Title

-----------

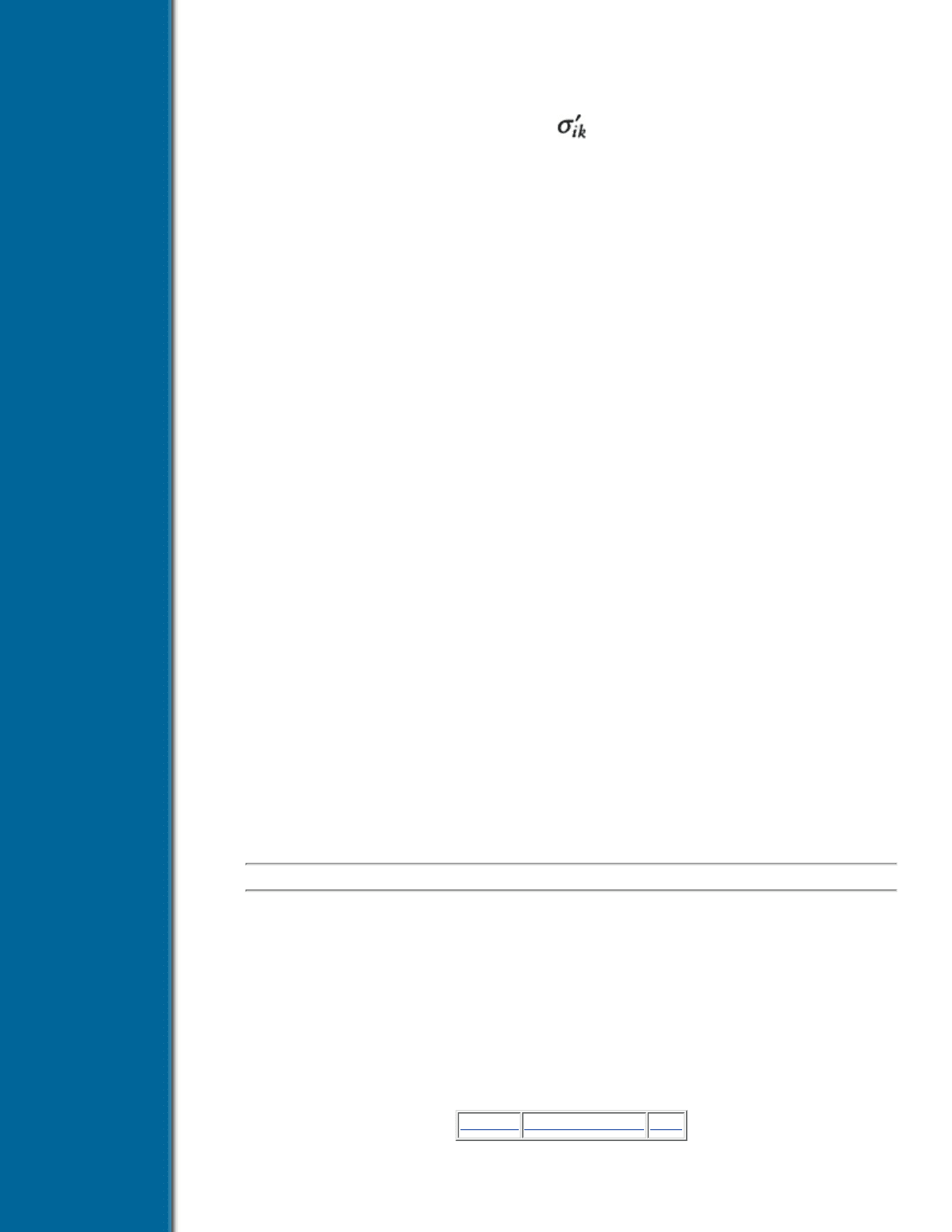
and the orientation of their arms indicates a fairly constant direction of the two transverse

eigenvectors—respectively, the least and most compressive eigendirections. The third helix exhibits a more

complex behavior, suggesting that the stress tensor is less uniform in the region of contact between the tubes

and the body than in other parts of the flow.

Figure 5.24 (bottom) shows the viscous stress tensor

in the same flow. As expected, the trajectories are

similar to those in Figure 5.24(top), but removing the large isotropic pressure contribution dramatically

enhances the anisotropy of the cross-section of the tubes. The surface corresponds to a constant eccentricity of

90 and is crossed twice by each tube.

5.5 Conclusions

A unified view of vector and tensor field visualization techniques in computational fluid dynamics has been

presented in this chapter. Many diverse application-dependent visualization mappings are described in a

unified framework by considering the semiotics of data representation and by identifying attributes of icons.

Visualization mappings are classified as a function of their object, spatial domain, and information level. Line

and surface icons improve the display of elementary information by using point icons. Local icons represent

data gradients, and global icons reveal the complete structure of the data field. The concepts are illustrated

here mainly by examples of aerodynamical flows, but apply to a much wider variety of data.

Undoubtedly, there are various types of icons suggested by our classification that are yet to be designed. For

example, empty boxes in Figure 5.2 suggest that research be carried out in order to design local surface icons

of vector fields, as well as elementary surface and local icons of tensor fields. In addition, global icons of

vector and tensor data must still be improved and new mappings are to be designed.

5.6 Appendix: Software Environments for Flow Visualization

This appendix completes the former theoretical discussion by describing actual implementations of various

visualization mappings. Many different software packages for scientific visualization have appeared during

the last few years, and extensive reviews are given, for example, in References [73, 74]. In the following, we

first discuss FAST, a powerful visualization environment that includes facilities for computational

aerodynamics. Then, we mention other visualization software capable of displaying scalar and vector fields.

To our knowledge, tensor field mappings have not yet been implemented in multipurpose visualization

packages, with the notable exception of NCSA’s RIVERS project [2].

FAST. (Flow Analysis Software Toolkit)

is a flow visualization environment made up of several programs

(modules) providing visualization tools for scalar and vector fields defined over single or multi-zoned grids

[75]. The user commands the different modules by means of interactive graphical interfaces built with the

Panel Library [76]. Every graphical object created with FAST, as well as grids, solution files, scalar and

vector fields, are placed in shared memory and are accessible by all modules. FAST currently runs on Silicon

Graphics 4D workstations. Its portability is enhanced, however, by the use of modular programming methods,

a graphics library standard, and common network communication protocols for the distribution of processing

(Unix sockets). In addition, FAST is extensible and facilities are provided for implementing new modules and

customizing the graphical interface.

Contact Cosmic, The University of Georgia, 382 East Broad Street, Athens, GA 30602-4272 USA.

FAST supports both structured and unstructured grid files and solution files, as well as any precomputed

scalar or vector data in PLOT3D format. FAST is also capable of loading and rendering ArcGraph metafiles

[77].

A calculator module computes various scalar and vector functions from the input data and performs different

mathematical operations on the resulting fields. It has the appearance and functionality of real programmable

calculators, but, instead of operating on numbers, it operates on fields of scalar numbers and vectors. More

than a hundred scalar and vector functions are preprogrammed, but the user can interactively create and

execute any formula that transforms scalar and vector fields.

Previous Table of Contents Next

reserved. Reproduction whole or in part in any form or medium without express written permission of

EarthWeb is prohibited. Read EarthWeb's privacy statement.

Search Tips

Advanced Search

Computer Visualization: Graphics Techniques for Engineering and Scientific Analysis

by Richard S. Gallagher. Solomon Press

CRC Press, CRC Press LLC

ISBN: 0849390508 Pub Date: 12/22/94

Search this book:

Previous Table of Contents Next

Another module displays grid geometry and performs surface rendering of scalar and vector fields across grid

planes; facilities include contour lines, arrows, displacement and polygonal surfaces. For example, this

module was used to render the body in Figure 5.4 and 5.18, the arrow plot in Figure 5.4, and the helicity

density contours in Figure 5.18. Most of the modalities for scalar fields are also available for unstructured

grids. An additional module discussed in length in Reference [35] computes scalar isosurfaces and cutting

planes of scalar and vector data.

Streamlines and rakes of streamlines can be computed interactively. Extraction and display of critical points,

vortex cores, and skin-friction topology are performed by a topology module [56, 48], a unique feature of

FAST that was used in Figures 5.16 and 5.18. The latest release of FAST includes an audio module,

streamribbons, and streamtubes, which was used to create Figure 5.12.

Software for distributed computing. As mentioned in Section 5.3.1.2, distributed computing is being explored

as an enabling technology for interactive flow visualization. Examples of NASA software linking Cray

supercomputers and Silicon Graphics workstations include a distributed version of PLOT3D and RIP, a

remote interactive particle tracer [40]. In addition, Cray supports a commercial version of MPGS

(Multi-Purpose Graphics System), a distributed graphics program providing facilities for structured and

unstructured data, such as arrows, particle traces, contour lines, and isosurfaces.

Other software. In addition to the general and flexible application builders which can be programmed for flow

visualization, such as apE,

AVS,

Explorer,

or Khoros

—other packages exist that are useful for

displaying scalar and vector data. For example,

TaraVisual Corporation, Inc.

Stardent Computer, Inc.

Silicon Graphics, Inc.

Available by anonymous ftp at pprg.eece.unm.edu in the U.S. and ftp.uni-erlangen.de in Germany.

VISUAL3,

displays the data in multiple windows containing correlated cursors—one window represents the

volumetric data and two other windows display 2-D and 1-D cuts. Specific facilities include streamribbons,

streamtubes, and X-Rays for rendering of scalar data [62, 78].

Massachussets Institute of Technology.

Title

-----------

VISAGE

—an object-oriented visualization system for structured or unstructured grids—provides facilities

such as isosurfaces, streamtubes, streamribbons, arrows and cutting planes [79].

General Electric Corporate Research and Development.

The Data Visualizer

handles structured and unstructured grids, and different versions exist for a large variety

of hardware configurations. Facilities include 2-D and 3-D graphics, arrows, cutting planes, streamlines,

volume rendering, and streamribbons.

Wavefront Technologies, Inc.

FIELDVIEW,

which runs on a variety of UNIX workstations, provides cutting planes, isosurfaces, arrows,

contour lines, streamlines, as well as a calculator module for field operations [80]. Finally,

Intelligent Light, Inc.

PV-WAVE

is a visualization package intended for the display and analysis of large multidimensional data

sets. It is not specifically intended for flow visualization but may be used to display scalar and vector data.

Precision Visuals, Inc.

5.6 Acknowledgements

The authors are grateful to J. Helman, M. Briscolini, P. Santangelo, J. Hultquist, W. Schroeder, C. Volpe, and

W. Lorensen for contributing images that greatly enhanced the scope of this chapter. Valuable comments on

earlier versions of this chapter were given by Paul Ning, Mark Peercy and Tomiko Yoda. Paul Ning

implemented the Marching Cubes algorithm on which our isosurface extraction algorithm is based. Yuval

Levy computed the data represented in Figures 5.22 and 5.24, Rogers et al.[81] computed the data in Figure

5.8, and Ying et al.[82] computed the data in Figures 5.4, 5.5 5.11, 5.16, 5.17 and 5.18. Cantwell and Coles

[83] measured the data displayed in Figures 5.14 and 5.15. Extensive use of FAST Beta version 2.1 greatly

facilitated this work. The authors are supported by NASA under contract NCA-781 which includes support

from the NASA Ames Numerical Aerodynamics Simulation Program and the NASA Ames Fluid Dynamics

Division, and also by NSF under grant ECS8815815.

Previous Table of Contents Next

reserved. Reproduction whole or in part in any form or medium without express written permission of

EarthWeb is prohibited. Read EarthWeb's privacy statement.

Search Tips

Advanced Search

Computer Visualization: Graphics Techniques for Engineering and Scientific Analysis

by Richard S. Gallagher. Solomon Press

CRC Press, CRC Press LLC

ISBN: 0849390508 Pub Date: 12/22/94

Search this book:

Previous Table of Contents Next

5.7 References

1 B. H. McCormick, T. A. DeFanti, and M. D. Brown, “Visualization in scientific computing: a

synopsis,” IEEE Computer Graphics and Applications, vol. 7, no. 4, pp. 61–70, 1987.

2 R. B. Haber, “Visualization techniques for engineering mechanics,” Computing Systems in

Engineering, vol. 1, no. 1, pp. 37–50, 1990.

3 R. B. Haber and D. A. McNabb, “Visualization idioms: a conceptual model for scientific

visualization systems,” in Visualization in Scientific Computing (G. M. Nielson and B. Shriver, eds.),

pp. 74–93, CS Press, Los Alamitos, CA, 1990.

4 R. Ning and L. Hesselink, “Fast volume rendering of compressed data,” in Proc. IEEE Visualization

’93, CS Press, Los Alamitos, CA., 1993.

5 A. I. Borisenko and I. E. Tarapov, Vector and Tensor Analysis with Applications. Dover

Publications, New York, 1979.

6 W. E. Lorensen and H. E. Cline, “Marching cubes: A high resolution 3-D surface construction

algorithm,” Computer Graphics, vol. 21, no. 4, pp. 163–169, 1987.

7 M. Levoy, “Display of surfaces from volume data,” IEEE Computer Graphics and Applications, vol.

8, no. 3, pp. 29–37, 1988.

8 R. A. Drebin, L. Carpenter, and P. Hanrahan, “Volume rendering,” Computer Graphics, vol. 22, no.

4, pp. 110–119, 1988.

9 T. Delmarcelle and L. Hesselink, “Visualizing second-order tensor fields with hyperstreamlines,”

IEEE Computer Graphics and Applications, vol. 13, no. 4, pp. 25–33, 1993. Special issue on scientific

visualization.

10 T. Delmarcelle and L. Hesselink, “Visualization of second order tensor fields and matrix data,” in

Proc. IEEE Visualization ’92, pp. 316–323, CS Press, Los Alamitos, CA., 1992.

11 C. Upson, R. Wolff, R. Weinberg, and D. Kerlick, Two and Three Dimensional Visualization

Workshop. ACM SIGGRAPH, 1989. SIGGRAPH 1989 course notes 13.

12 M. M. Blattner, R. M. Greenberg, and M. Kamegai, “Listening to turbulence: an example of

scientific audiolization,” in Multimedia Interface Design (M. M. Blattner and R. B. Dannenberg, eds.),

ch. 6, ACM Press, Addison-Wesley, New York, 1992.

Title

-----------