Решение задач из сборника Павлова К.Ф., Романкова П.Г., Носкова А.А. 1. Основы прикладной гидравлики

Подождите немного. Документ загружается.

1) Физические свойства диоксида углерода при 75 °C и избыточном давлении

2 кгс/см

плотность – по формуле (1.5)

525,4

34810013,1

)1081,9210013,1(273

4,22

кг

ТР

РТ

абсо

СО

⋅⋅

⋅⋅+⋅⋅

⋅=

⋅

⋅=

;

динамический коэффициент вязкости по номограмме VI:

µ = 0,017·10

-3

Па·с.

2) Массовая скорость движения диоксида углерода представляет собой:

mass

= ρ·W [кг/м

· м/с = кг/(м

·с)];

W =

.6,6

4,525

mass

3) Критерий Рейнольдса:

Re =

175676

100,017

4,5250,16,6

экв

⋅

4) Коэффициент трения найдём по формуле (1.42):

























+⋅−=

9,0

81,6

7,3

lg2

;

выразим λ:

.03431,0

175676

81,6

3,7100

0,7

lg4

81,6

7,3

lg4

9,0

























⋅

























+⋅

5) По таблице XIII находим коэффициенты местных сопротивлений:

колено

кол

(для диаметра 100 мм данных нет, но при увеличении диаметра на

25 мм коэффициент сопротивления уменьшается в 2 раза) = 0,3

задвижка

задв

= 0,5;

вход в трубу

вх

= 0,5;

.2,25,05,03,044 =++⋅=++⋅=

∑

вхзадвкол

ξξξξ

6) Находим полное гидравлическое сопротивление сети по формуле (1.49):

=−+⋅⋅+













⋅

+⋅

⋅

=∆

∑

)(1

экв

PPHg

ρξ

λρ

Па6,33582,2

1,0

9003431,0

525,46,6













⋅

+⋅

⋅

7) Определяем объёмный расход газа:

G = ρ·W·S = W

mass

·S;

Q = W·S =

.052,0

4525,4

1,0785,030

322

мdWSW

massmass

⋅

⋅⋅

⋅

⋅⋅

⋅

8) Находим мощность потребляемую насосом по формуле (1.33):

кВт



35,0

0,51000

6,33580,052

1000

⋅

∆

⋅

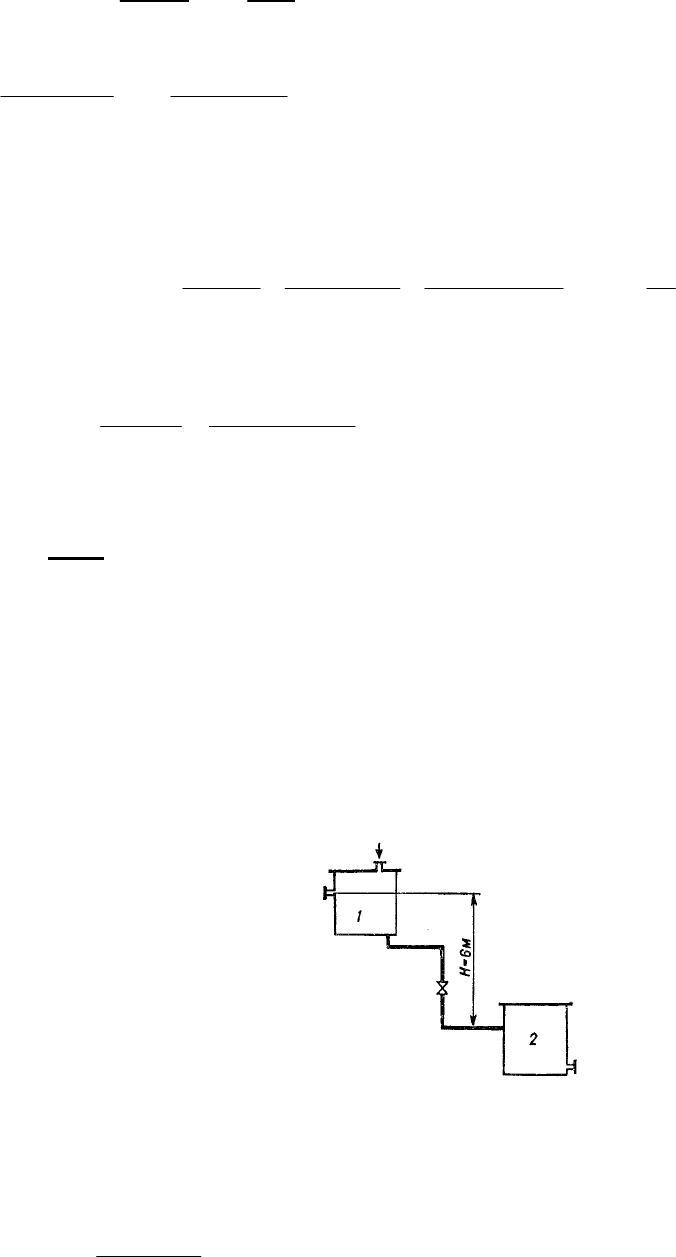
№46. 40%-ный этиловый спирт спускается из бака по трубе

диаметром 33,5

2,8 мм. На трубе имеются кран и 2 колена под углом 90°.

Общая длина трубопровода 49 м. Определить скорость спирта в

трубопроводе (при разности высот 7,2 м). Коэффициент трения принять

приближённо равным 0,025. Найдя скорость спирта проверить значение

коэффициента трения. Температура спирта 35°С.

К этой задаче см. пример 1.28. Рисунок не к этой задаче, а просто для нагляд-

ности.

1) Физические свойства 40%-ного этанола при 35 °C находим интерполяцией

табличных значений:

ρ = 935 – (935 – 923)·15/20 = 926 кг/м

(табл. IV);

µ =

48,102,2

= 1,75 мПа·с = 1,75·10

-3

Па·с (табл. IX).

2) Запишем уравнение Бернулли (формула 1.27а):

000-0

0-0

111-1

1-1

Z +

⋅

−

ρρ

Сечение (1-1) расположим на поверхности жидкости в баке 1, скорость

движения жидкости в нём W

1-1

можно приближённо принять равной нулю. За

нулевое (0-0) сечение возьмём место входа трубы в бак, который принимает

спирт, т.е. Z

0-0

= 0, а Z

1-1

= 7,2 м, Р

0-0

= Р

1-1.

м.с.тр

001-1

ZZ ++

⋅

=−

−−

−

Умножим правую и левую части на ρ·g:

..тр

см

Hg ++

⋅

=⋅⋅

−

или













⋅

=⋅⋅

∑

−

3) По таблице XIII находим коэффициенты местных сопротивлений:

колено

кол

(для условного прохода 27,9 мм) = 2;

кран

= 2;

вход в трубу

вх

= 0,5;

.5,65,02222 =++⋅=++⋅=

∑

вхкранкол

ξξξξ

4) Выражаем скорость движения спирта:

.7,166,1

5,6

0279,0

49025,0

2,781,92

W ≈=













⋅

⋅⋅













⋅

+⋅

⋅⋅⋅

∑

−

5) Проверяем значение коэффициента трения:

а) критерий Рейнольдса:

Re =

25097

101,75

9260,02791,7

экв

⋅

б) подбором параметра в Exсel выяснил, что трубопровод имеет

шероховатость стенки е = 0,015 мм, что соответствует алюминиевым

технически гладким трубам (в примере 1.28 те же трубы).

Для гидравлически гладких труб коэффициент трения находим по

формуле (1.40):

0251,0

25097

316,0

25,00,25

===

- т. е. коэффициент трения был принят

достаточно точно.

№47. По трубопроводу диаметром 26,8

2,5 мм стекает нитробензол

с температурой 44 °С. Начальная точка трубопровода выше конечной на

200 мм. Длина горизонтальной части трубопровода 242 м. Учесть только

сопротивление трения. Найти массовый расход нитробензола и

проверить принятый режим его движения.

1) Физические свойства нитробензола при 44°С находим интерполяцией

табличных значений:

ρ = 1183 – (1183 – 1163)·4/20 = 1179 кг/м

(табл. IV);

µ = 1,44 – (1,44 – 1,24)·4/10= 1,36 мПа·с = 1,36·10

-3

Па·с (табл. IX).

2) Трубопровод состоит из прямого участка длиной 242 м, соединённого с

начальной точкой двумя отводами и перемычкой.

Запишем уравнение Бернулли (формула 1.27а):

000-0

0-0

111-1

1-1

Z +

⋅

−

ρρ

Сечение (1-1) расположим на уровне оси потока нитробензола в начальной

точке трубопровода. За нулевое (0-0) сечение возьмём ось потока прямого

участка трубы, уровень которой ниже сечения (1-1) на 200 мм, т.е. Z

0-0

= 0, а

1-1

= 0,2 м, Р

0-0

= Р

1-1

, скорости потока в обоих сечениях можно приближённо

считать равными W

0-0

= W

1-1

м.с.трп001-1

hhhНZZ

−

По условию h

м.с.

= 0, т. е. H = h

тр

3) Потери напора связаны со скоростью движения потока формулой (1.36), но

так как нам нужно, чтобы они были выражены в метрах эту формулу

необходимо привести к виду:

ПаР

⋅

⋅⋅=

⋅

⋅⋅=

⋅

⋅⋅

⋅

∆

][

]м[

λλ

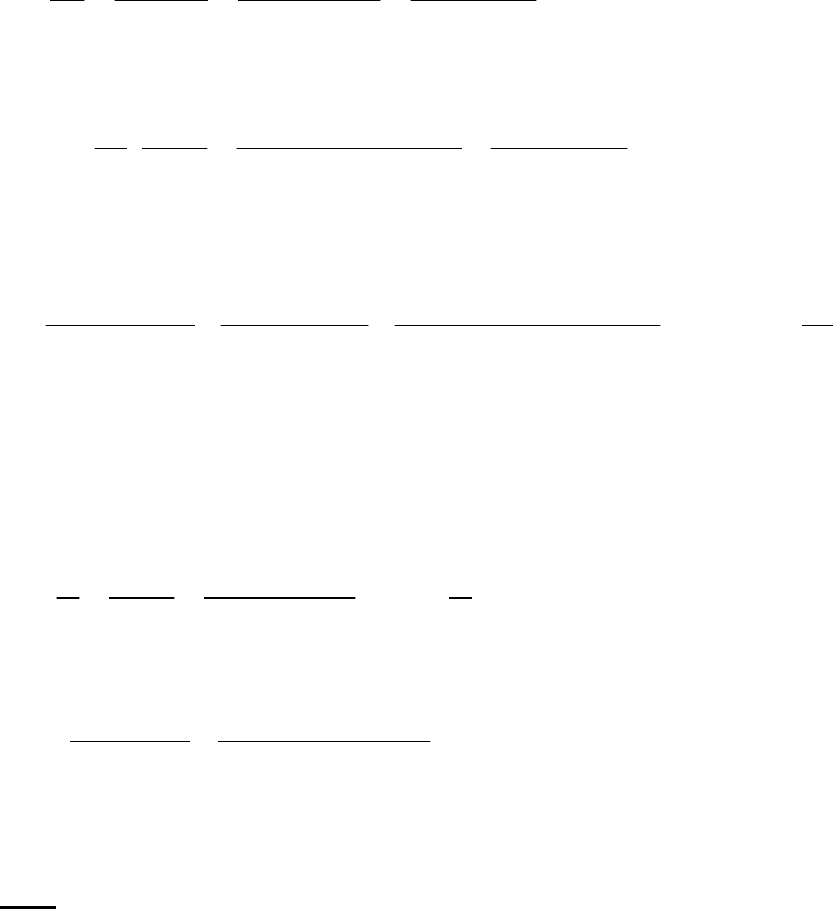
4) Примем для начала ламинарный режим течения нитробензола, тогда

коэффициент трения рассчитывается по формуле (1.38):

πµ

⋅

⋅⋅⋅

⋅⋅

⋅

6464

5) Подставляем в выражение потерь напора:

gdQ

QLd

⋅⋅⋅

⋅⋅⋅⋅

⋅⋅⋅⋅⋅⋅

⋅

⋅⋅=

πρ

πµ

425

тр

1288168

6) Выражаем объёмный расход нитробензола:

диаметр трубопровода округлим до 0,022 м

gdН

gdh

00004039,0

2421036,1128

81,914,3022,011792,0

128128

⋅⋅⋅

⋅⋅⋅⋅

⋅⋅

⋅⋅⋅⋅

⋅⋅

⋅⋅⋅⋅

−

πρ

7) Массовый расход нитробензола находим по формуле (1.18):

G = Q·ρ = 0,00004039·1179 = 0,0476 кг/с = 4,76·10

-2

кг/с.

8) Проверяем принятый режим течения:

а) скорость потока – из формулы (1.17):

W 106,0

0,0220,785

,0000403904

⋅

;

б) критерий Рейнольдса:

Re =

2022

101,36

11790,0220,106

экв

⋅

< 2320 - ламинарный режим

принят правильно.

№48. В аппарат, работающий под давлением Р

абс

= 0,2 МПа, надо

подавать насосом воду из открытого резервуара по трубопроводу

внутренним диаметром 70 мм. Верхняя точка трубопровода выше

уровня воды в резервуаре на 5 метров. Расчётная длина трубопровода

(собственная плюс эквивалентная длина местных сопротивлений) 350 м.

Коэффициент трения λ = 0,03. Найти зависимость между расходом воды,

протекающей по трубопроводу и потерей давления на преодоление всех

сопротивлений трубопровода (найти уравнение характеристики сети).

В общем случае полное гидравлическое сопротивление сети рассчитывается

по формуле (1.50):

(

)

).(

экв

РРHg

−+⋅⋅+

⋅













+⋅

+=∆

∑

Для следующей задачи нам нужно гидравлическое сопротивление,

выраженное в метрах. Для этого поделим обе части этого выражения на ρ·g:

(

)

РР

⋅

−

⋅













+⋅

∑

)(

экв

По формуле (1.17) скорость потока:

Q = W·S;

W =

⋅

Подставляем:

(

)

РР

⋅

−

⋅⋅

⋅













+⋅

∑

)(

экв

Плотность воды примем равной 1000 кг/м

81,91000

10013,1102,0

81,907,014,3

07,0

35003,0

⋅

⋅−⋅

⋅⋅

⋅













⋅

;

h = 15 + 520171·Q

– это и есть уравнение характеристики сети.

№49. Центробежный насос имеет следующую паспортную

характеристику:

Расход воды м

/ч 12 18 24 30

Создаваемый напор, м

38 36 32 26

Сколько воды будет подавать этот насос, если поставить его работать на

сеть задачи 48? (Найти рабочую точку).

Представленные в условии данные являются точками кривой характеристики

насоса.

В прошлой задаче было составлено уравнение характеристики сети:

h = 15 + 520171·Q.

Чтобы графически его изобразить для нескольких произвольных значений

расхода найдём потери напора:

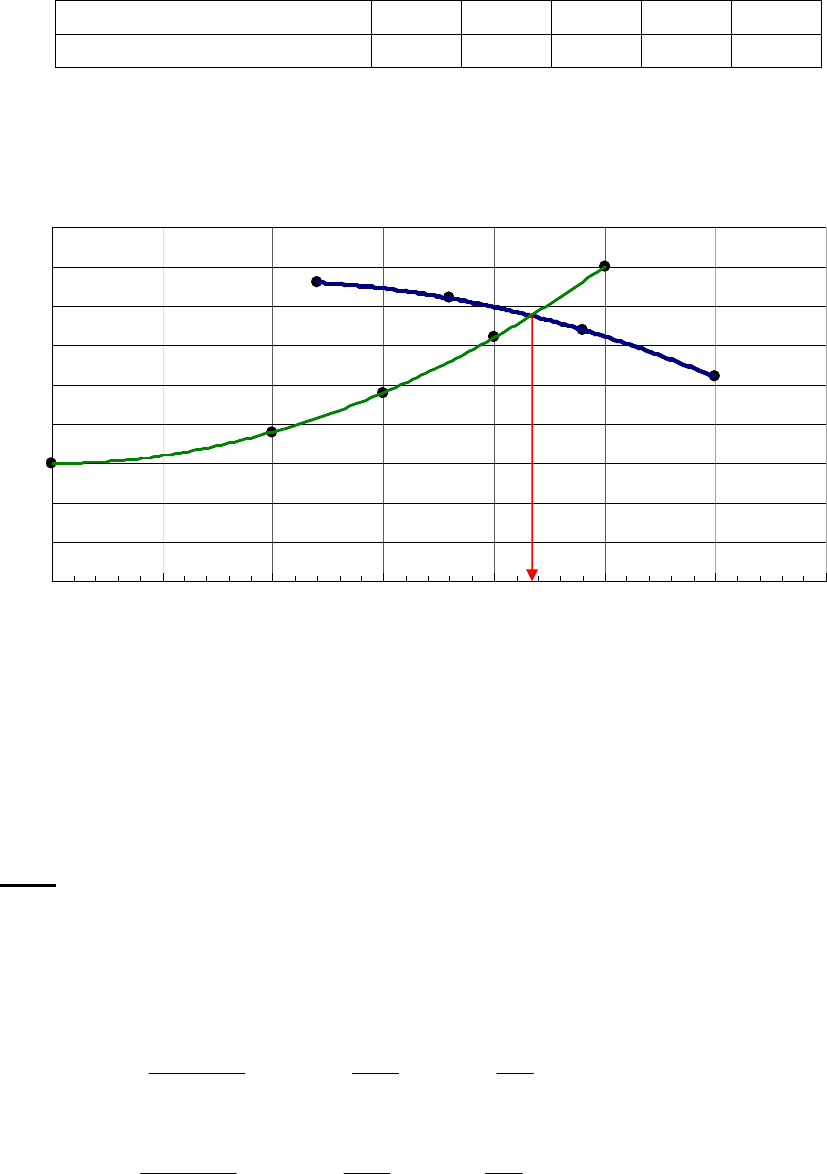
Расход воды м

/ч 0 10 15 20 25

Потери напора, м 15 19 24 31 40

Рабочая точка насоса находится на пересечении кривых этих двух характе-

ристик:

0 5 10 15 20 25 30 35

Расход м

/ч

Напор, м

По графику видно, что данный насос при работе на эту сеть будет подавать

21,7 м

/ч воды.

№50. Вентилятор подаёт воздух, засасывая его из атмосферы.

Подача вентилятора 12500 м

/ч. Какое массовое количество воздуха

подаёт вентилятор зимой (при t = -15°С) и летом (при t = 30°С)?

1) Найдём плотность воздуха при этих температурах по формуле (1.5):

368,1

258

273

293,1

кг

ТР

РТ

абсо

оС

=⋅=

⋅

⋅=

°−

ρρ

;

165,1

303

273

293,1

кг

ТР

РТ

абсо

оС

=⋅=

⋅

⋅=

ρρ

2) По формуле (1.18) ищем массовый расход:

G = ρ·Q.

Зимой:

зим

= 12500·1,368 = 17100 кг/ч = 1,71·10

кг/ч.

Летом:

лет

= 12500·1,165 = 14563 кг/ч

≈

1,46·10

№51. Определить давление, развиваемое вентилятором, который

подаёт воздух из атмосферы при 18 °С в пространство с избыточным

давлением 43 мм вод. ст. Потери давления в трубопроводе 275 Па,

скорость воздуха в нём 11,5 м/с.

1) Найдём плотность воздуха при температуре 18 °C по формуле (1.5):

ТР

РТ

абсо

⋅

⋅=

ρρ

;

абс

= Р

атм

+ Р

изб

Переведём Р

изб

в паскали:

101300 Па ------ 10330 мм вод. ст.

Х ------ 43 мм вод. ст.

Х= Р

изб

= 422 Па;

218,1

29110013,1

)42210013,1(273

293,1

кг

⋅⋅

+⋅⋅

⋅=

2) Давление, развиваемое вентилятором, находим по формуле (2.9):

( )

Па

РРРР

пот

5,777

5,11218,1

275422

⋅

++=

⋅

+∆+−=∆

№52. Какое абсолютное давление (в кгс/см

) должен иметь воздух,

подаваемый в монтежю для подъёма серной кислоты относительной

плотности 1,78 на высоту 21 м? Гидравлическими потерями пренебречь.

1) Плотность кислоты - по формуле (1.2):

ρ = ∆·ρ

= 1,78·1000 = 1780 кг/м

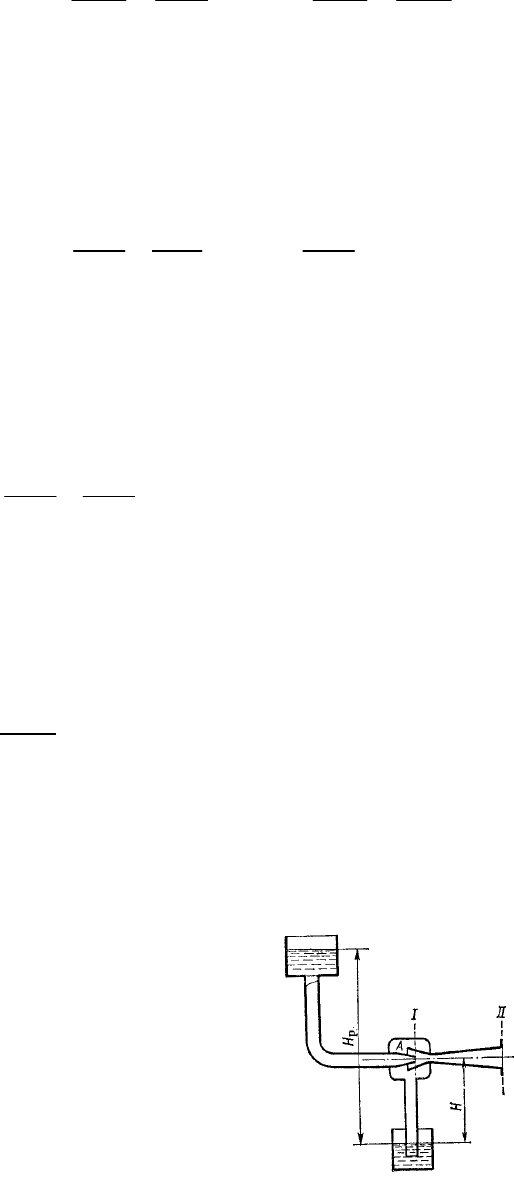
2) Запишем уравнение Бернулли без учёта гидравлических потерь (формула

1.27):

⋅

−

000-0

0-0

111-1

1-1

ρρ

Сечение (1-1) расположим на уровне оси потока кислоты в верхней точке

трубопровода (стрелочка с подписью «кислота»). За нулевое (0-0) сечение

возьмём уровень кислоты в монтежю, т.е. Z

0-0

= 0, а Z

1-1

= 21 м, скорости

движения кислоты в сечении (0-0) равно нулю: W

0-0

= 0.

0-0

111-1

⋅

−

ρρ

Наша задача – найти разность давлений Р

0-0

и P

1-1

, при этом Р

1-1

= P

атм

, т. к.

сечение расположено на оси потока и вышестоящего столба жидкости в нём

нет. Минимальное давление, обеспечивающее перемещение жидкости,

соответствует предельной скорости W

1-1

= 0:

;

0-011

1-10-0

ZZ −=

⋅

−

⋅

−

ρρ

0-0

– P

1-1

= ρ·g·(Z

1-1

– Z

0-0

) = ρ·g·H = 1780·9,81·21 = 366698 Па =

= 366698/(9,81·10

) = 3,74 кгс/см

№53. Скорость струи на выходе из диффузора горизонтального

водоструйного насоса 2,35 м/с. Вода выходит из диффузора под

атмосферным давлением. Диаметр выходного отверстия диффузора

62 мм, диаметр отверстия сопла (сечение I) 30 мм. Пренебрегая

потерями, определить теоретическую высоту H на которую может быть

поднята откачиваемая вода из открытого резервуара.

К этой задаче см. пример 2.8.

Сначала нужно найти теоретическое разрежение в камере А, а уже из него

выразить теоретическую высоту.

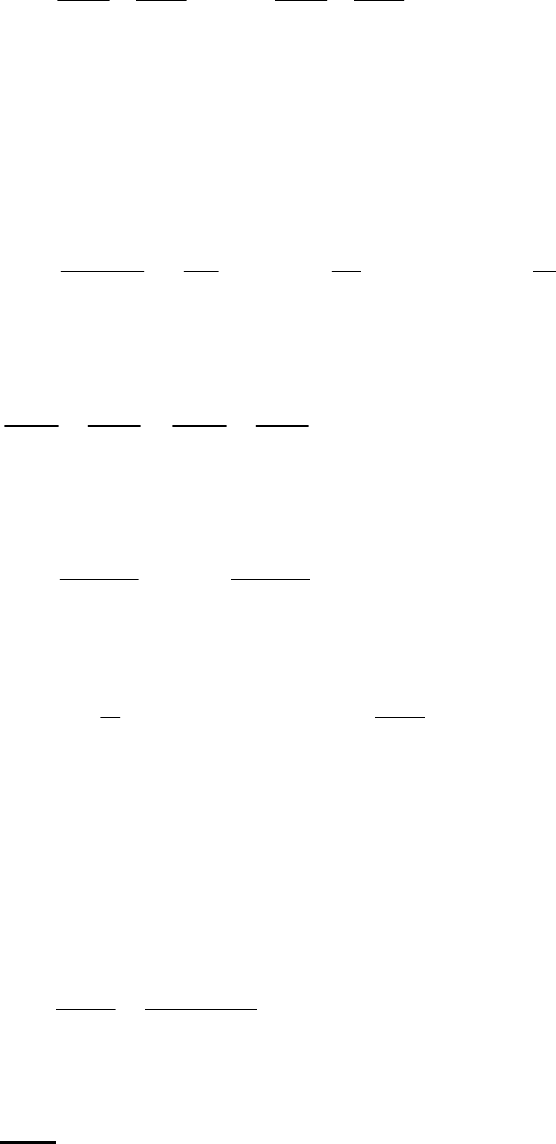
1) Запишем уравнение Бернулли для сечений I и II без учёта потерь (формула

1.27):

III

⋅

ρρ

При горизонтальном расположении насоса Z

= Z

. Скорость на выходе из

диффузора W

= 2,35 м/с, давление на выходе Р

– атмосферное. Скорость

потока в сечении I выразим из уравнения неразрывности:

·S

= W

·S

;

IIII

04,1035,2

=⋅













=⋅













⋅

2) Ищем теоретическое разрежение, равное Р

атм

– Р

III

⋅

⋅ 2g

ρρ

Умножим обе части на ρ·g:

III

WW ⋅

⋅

ρρ

;

примем плотность воды равной 1000 кг/м

;

(

)

(

)

.5366004,1035,2

1000

10013,1

22522

ПаWWPP

IIIIII

=−⋅+⋅=−⋅+=

Теоретическое разрежение:

теор

= Р

атм

– Р

= 1,013·10

– 53660 = 47640 Па.

Теоретическую высоту находим из выражения:

теор

= ρ·g·H;

теор

85,4

81,91000

47640

⋅

№54. Определить гидравлическое сопротивление слоя сухой

насадки высотой 3 м, состоящей из керамических колец 15

2 мм.

Через насадку просасывается воздух при 20 °С и атмосферном давлении

со скоростью 0,4 м/с (скорость фиктивная).

1) Физические свойства воздуха при температуре 20 °C: