Презентация - Семенкин Е.С. Методы оптимизации
Подождите немного. Документ загружается.


Метод квадратичной интерполяции
Еслиизвестнызначенияфункции f(x) втрехточках α, β, γ, равные f
α
, f
β
, f
γ
, то
функция f(x) можетбытьаппроксимированаквадратичнойфункцией ϕ(x)=Ax
2
+Bx+C,
где A,B,Cопределяютсяизсистемыуравнений
A α
2
+Bα+C=f
α
,
Aβ
2
+Bβ+C=f
β
,
Aγ
2
+Bγ+C=f
γ
,
тоестьизсистемытрех линейных уравненийстремянеизвестными.
Таккакквадратичнаяфункция ϕ(x) имеетминимумвточке -B/2A, если A>0, то
точкаминимума f(x) можетбытьаппроксимированазначением
Опишемалгоритм. Пусть f(x) - унимодальнаяфункцияоднойпеременной,A-
начальнаяаппроксимацияположенияминимума, длинашага H являетсявеличиной
тогожепорядка, чтоирасстояниеотточки A доистинногоминимума (условие,
котороенепростоудовлетворить).
Алгоритмквадратичнойинтерполяции:
1. Вычислить f(A), f(A+H).
2
.
Если
f
(A)<
f
(A+H),
то
взять
в
качестве
третьей
точки
A
-
H
и
вычислить
f
(A
-
H)
.
В
(
)
(
)
(
)
( ) ( ) ( )
.
2
1
222222
γβα
γβα
βααγγβ
βααγγβ
δ
fff
fff
−+−+−
+−+−
=
−
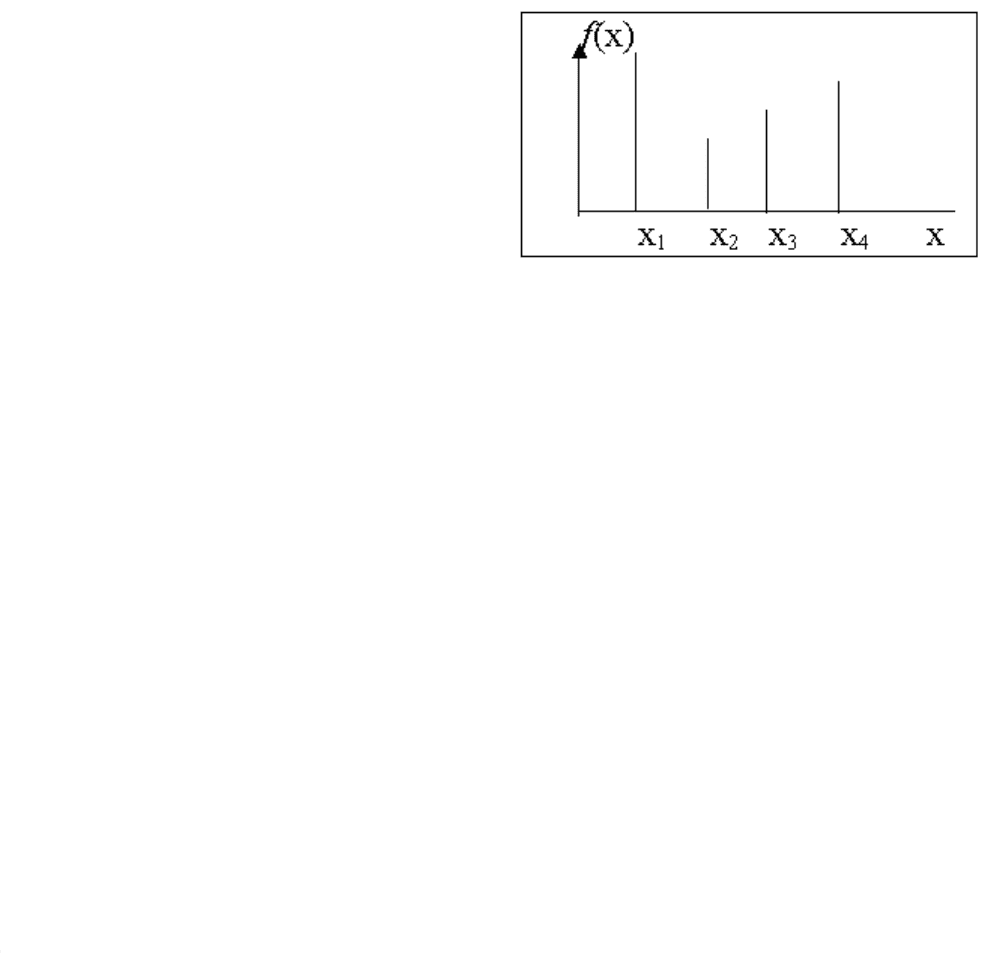
5. Еслипроцедуранезавершиласьнашаге 4, тоточкаснаибольшимзначением
отбрасываетсяивыполняетсяпереходнашаг 3. Ноесли, оставивточкуснаибольшим
значением, мыопределимконечныеграницыинтервала, вкоторомлежитминимум, то
следуетдействительнооставитьэтуточку, отброситьдругуюивернутьсянашаг 3.
Рис. 2. Выбор границ интервала
Впримеренарисунке 2 оставляем x
1
, x
2
, x
3
, ане x
2
, x
3
, x
4
, хотя x
1
идаетнаибольшее
значениефункции.
ОписаннаяпроцедураквадратичнойинтерполяцииназываетсяметодомПауэллаи
является частным (но наиболее часто используемым) случаем так называемого
интерполяционногометодаЛагранжа, которыйпредусматриваетаппроксимациюцелевой
функцииполиномамилюбогопорядка (анетольковторого). Наиболееэффективнаэта
процедураприоптимизацииквадратичныхилиблизкихкнимфункций. Вдругихслучаях
этотметодможетбытьнестольэффективным.
Дляоптимизациинеквадратичныхфункцийпредложенамодификацияэтогометода,
состоящаявтом, чтодляинтерполяциивыбираютсянетри, а четыре точки. Приэтомдве
внутренниеточкииспользуютсяпоочередискрайнимиточкамидляпостроения двух
аппроксимаций точки минимума, выполняемых по алгоритму Пауэлла. Затем их
взвешенная средняя выбирается для новой итерации. Такая процедура повышает
надежность
определения
точки
минимума
для
функций,
не
являющихся
квадратичными
.
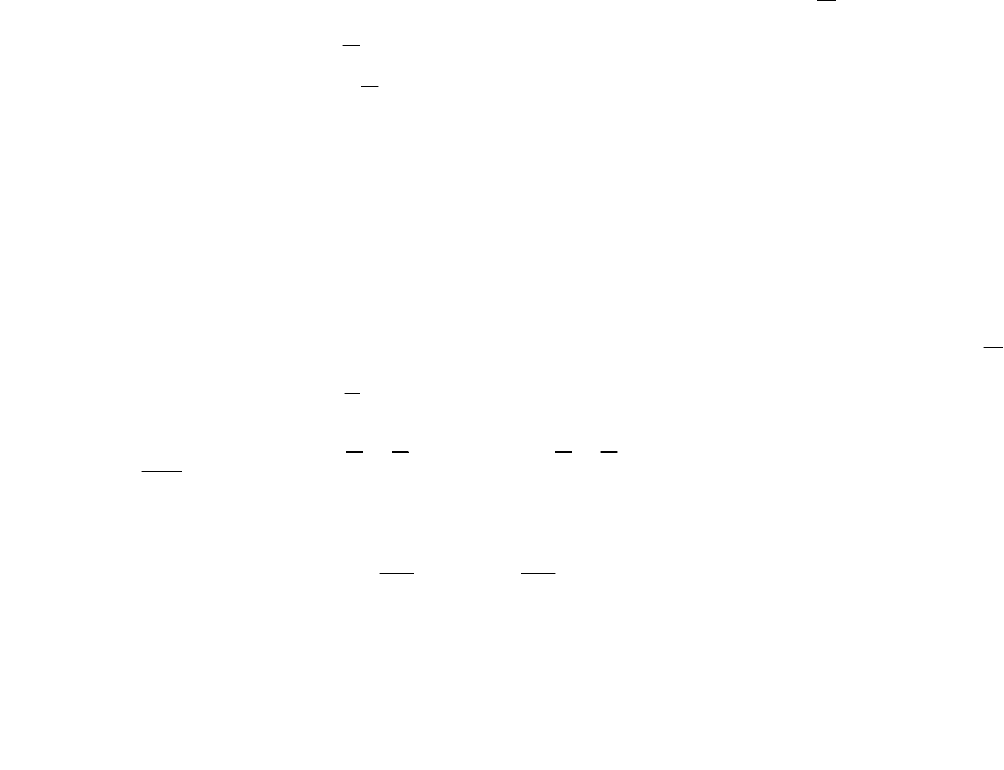
Метод кубической интерполяции
Прирешенииреальныхзадачредкоприходитсяиметьделосфункциямиодной
переменной. Однако методы одномерной оптимизации важны при многомерной
оптимизации, котораявыполняетсявосновномпоследующемуправилу: зафиксировать
некоторую точку, выбрать подходящее направление, выполнить одномерную
оптимизацию из выбранной точки в выбранном направлении. Поэтому методы
интерполяцииполезныдлявыполнениялинейногопоискаприоптимизациифункций
многихпеременных. Вэтомслучаеобычнотребуетсянайтиминимумфункции f(x) в
точкахпрямой x
2
, x
3
, x
4
, где X
0
- заданнаяточка, - определенноенаправление. Значение
функции наэтойпрямойявляютсязначениямифункцииоднойпеременной λ:
РассмотримметодДэвидона, вкоторомфункцияаппроксимируетсякубическим
полиномом, икоторыйобеспечиваетбольшуюточностьопределенияточкиминимума.
Обсуждениеметодапроведемввиде, пригодномдлямногомернойоптимизации.
Для интерполяции используются значения функции и ее производной,
вычисленныевдвухточках.
Пустьминимизируетсяфункция f(x) напрямой , тоестьфункция
Предполагаем, чтоизвестныследующиезначения:
d
(
)
fX d
0
+λ
(
)
.)(
0
dXf λλϕ +=
X d
0
+
λ
(
)
(
)
(
)
ϕ h fX hd fx hdx hd x hd
n n
= + = + + +
0 1
0
1 2
0
2
0
, ,..., .
(
)
(
)
.
00
ddhXgddhXf
h
ΤΤ
+=+∇=
∂
∂ϕ
() () () ()
.,,,
qpqp
Gq
h
Gp
h
qp ====
∂
∂ϕ
∂
∂ϕ
ϕϕϕϕ

Есливыбрать p=0(дляпростоты), тоуравнения, определяющие a,b,c,d, выглядят
так:
Этиуравненияимеютрешение:
Стационарныеточкикубическогополиномаявляютсярешениемуравнения
Точкойминимумакубическогополиномаявляется
(*)
Какужеотмечалось, этовсевыполняетсяпри p=0. Выбор q осуществляетсяиз
следующихсоображений.
Если
G
p
<
0
,
то
следует
выбирать
q
>
0
,
то
есть
сделать
шаг
в
направлении
убывания
a
a bq cq dq
b G
b cq dq G
p
q
p
q
=
+ + + =
=
+ + =
ϕ
ϕ
2 3
2
2 3
(
)
(
)
( )
.
3
,3/2 ,/ , ,
qp
qp
qpppp
GG
q
Z
qZGGdqZGcGba
++
−
=
+
+
=
+
−
=
=
=
ϕϕ
ϕ
( ) ( )
G G Z
h
q
G G Z
h
q
p p p q
− + + + +
=2 2 0
2
.
,
2
+−
−+
=
WGG
GWZ
qr
pq
p
W
Z GG
p q
= −
2
1
2

Дэвидон, ФлетчериПауэллпредложиливыбирать q следующимобразом:
, где ϕ
m
- оценканаименьшегозначения ϕ(h), η =const(2 или 1).
Алгоритмкубическойинтерполяции.
1. Найти ϕ
p
=f(X
0
) и .
2. Проверить, выполняетсялиусловие G
p
<0. Еслиневыполняется, производитьпоиск
внаправлении , иначе - внаправлении . Выбрать q всоответствиисрекомендациями
(приэтомнеобходимо "угадать" ϕ
m
).
3. Вычислить
4. Если G
q
>0 или ϕ
q
> ϕ
p
, тоинтервал, содержащийминимум, найден. Иначеположить
q =2qиперейтик3.
5. Использоватьвыражение (*) дляаппроксимацииточкиминимуманаинтервале
(0, q) значением r.
6. Если , где ε - заданнаяточность, тоостановиться.
7. Вернутьсянашаг 5, используяинтервал (0,r), если G
r
>0, либоиспользуяинтервал
(r,q), если G
r
<0.
(
)
q
G
p m
p
= −
−
min ,η
ϕ ϕ2
(
)
(
)
G gX d
p
=
0
Τ
d−
d
(
)
ϕ
q
fX qd= +
0
( )
[ ]
∂ϕ
∂
ε
h
gX hd d G= + = <
0 0
Τ
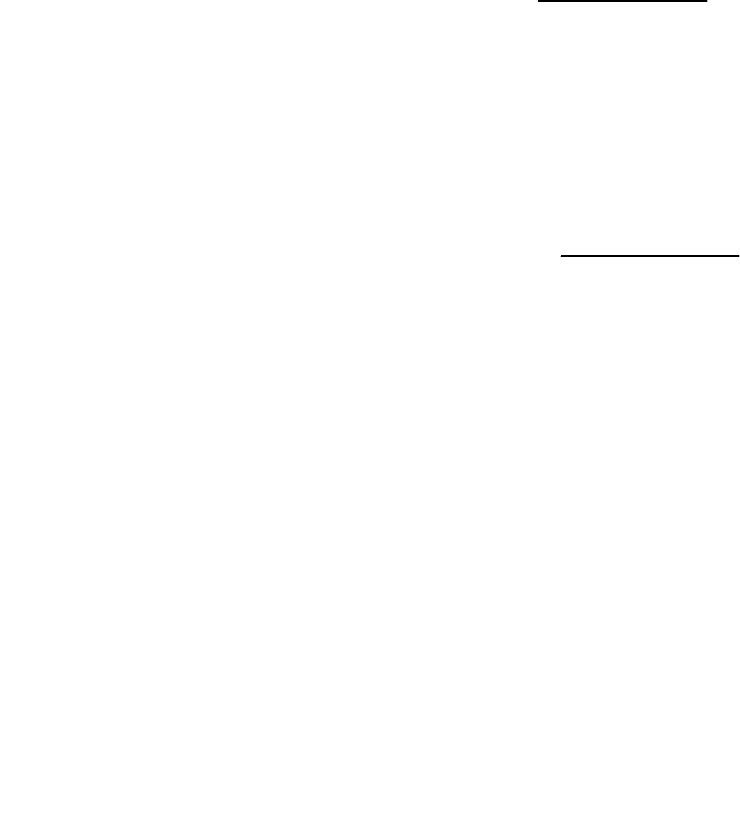
Итерационный метод regula falsi
Хорошоизвестный методсекущих отысканиянуляфункциипервоначально
назывался методом regula falsi или regula falsorum. Этот метод правильно
предсказываетположениенуляфункции, еслионазависитлинейноотсвоего
аргумента. Еслиданыдветочки a и b изначенияфункциивних, тоформула
предсказанияположениянуляфункцииимеетвид:
c = a-f(a) .
Так как процесс отыскания точки минимума целевой функции можно
интерпретироватькакотысканиенуляеепроизводной, тометодсекущихможетбыть
легкоиспользовандляцелейоптимизации. Формулапредсказанияположениянуля
производной (тоестьточкиминимума) принимаетвид:
c = a–f’(a) .
Если f'(с)≠0, топроцедураможетбытьпродолженаитеративносиспользованием
уменьшенногоинтервала [a,c], если f'(c) и f'(b) имеютодинаковыйзнак, или [c,b], если
f'(c) и f'(a) имеютодинаковыйзнак. Если f'(a) и f'(b) имеютодинаковыйзнак, тоточка c
должналежатьвнеотрезка [a,b]. Если f'(c) имеетопятьтотжезнак, то c заменяетту
точку, котораядаетнаибольшеезначениепроизводной. Если f'(c) имеетдругойзнак, то
можнопродолжатьпроцедуру regulafalsi итеративнодотехпор, поканебудет
полученаточкаснулевой (илидостаточномалой) производной.
Метод
работает
надежно
только
в
случае,
если
функция
почти
линейна
или
хотя
)()( afbf
ab
−
−
)()( afbf
ab
′
−
′
−

Итерационный метод Ньютона-Рафсона
ИнтерполяционнаяформулаНьютонадляулучшенияприближенногорешения
уравнения f(x)=0
x
k+1
= x
k
– f(x
k
)/f'(x
k
)
используеттолькооднуточку, нотребуетоценкизначенияфункциииее
производной. Еслифункциялинейнапо x, тонольфункциибудетуказанточно, в
противномслучаебудетполученотолькоулучшенноезначениеипроцессдолжен
бытьповторен. Какивпредыдущемслучаеэтарекуррентнаяформуламожетбыть
примененадляпоискануляпроизводной, тоестьдляопределенияточкиминимума
самой функции. Соответствующая итерационная формула, называемая также
правиломНьютона-Рафсона, имеетвид:
x
k+1
= x
k
– f'(x
k
)/f''(x
k
).
Еслицелеваяфункциянеявляетсяквадратичной, топонадобитсянесколько
итерацийдотехпор, поканебудетудовлетворенкритерийостанова.
Существенным
преимуществом
алгоритма
является
то,
что
требуется
только
одна

Однакоимеютсяинедостатки:
- еслиперваяивтораяпроизводныеоцениваютсяприближеннопоконечным
разностям, то эффективность алгоритма снижается не только из-за ошибок
округления, но и из-за неточности аппроксимации. Это особенно верно в
окрестноститочкиминимума, гдеперваяпроизводнаястановитсясущественно
малой;
- неразличаютсяточкиминимумов, максимумовиперегибов. Ужестартовая
точкадолжнавыбиратьсякакможноближекискомомуминимуму;
- если целевая функция имеет порядок выше второго, то итерации метода
Ньютона-Рафсона могут не сойтись.
Условиемсходимостиявляетсяположительностьвторойпроизводнойдлявсех
точек, встречающихсявпроцессеоптимизации.
Вообщеговоря, надежностьискоростьсходимостивсехинтерполяционных
алгоритмовсущественнозависитоттого, насколькоцелеваяфункциисоответствует
модельнойфункции, положеннойвосновуметода. Внекоторыхслучаяхметоды
деленияинтервалаоказываютсялучше, чеминтерполяционные. Например, поиск
Фибоначчиэффективнеекубическойинтерполяциивслучаелогарифмической
функцииивслучаеполиномавысокойстепени. Поэтомуразрабатываютсяновыеи
болеесложныесхемыодномернойоптимизации, базирующиеся, восновном, на
всевозможных комбинациях интерполяционных подходов и методов деления

Оптимизация функций многих переменных
Разнообразныеметодымногомернойоптимизацииразличаютобычноповиду
информации, котораянеобходимаимвпроцессеработы:
- методыпрямогопоиска (методынулевогопорядка), которымнужнытолько
значенияцелевойфункции;
- градиентныеметоды (методыпервогопорядка), которымдополнительно
требуютсячастныепроизводныепервогопорядкацелевойфункции;
- ньютоновскиеметоды (методывторогопорядка), которыеиспользуюти
частныепроизводныевторогопорядка.
Рекуррентнаясхемабольшинстваметодовмногомернойоптимизацииоснована
навыражении
X
k+1
= X
k
+ λ
k
s
k
.
Ониотличаютсядруготдругаспособомвыборадлинышага λk инаправления
поиска s
k
. Первыйизних - этоскаляр, авторой - векторединичнойдлины.
Каквидно, методымногомернойоптимизациисводятсявтойилиинойформек
методамодномернойоптимизации. Историческипервымиподходамибылипрямые
обобщения одномерных методов (например, поиск Фибоначчи или
интерполяционныеметоды) намногомерныезадачи. Этиподходынебылиособенно
удачнымивсвязистем, чтоихтрудоемкостьрослаэкспоненциальносростом
размерностизадачи ("проклятиеразмерности" поБеллману).
Все
обсуждаемые
ниже
методы
предполагают
ту
или
иную
степень
гладкости

Методы прямого поиска
Методыпрямогопоискаявляютсяметодами, которыеиспользуюттолько
значенияфункцийинеиспользуютникакойвнутреннеймоделицелевойфункции.
Вместоэтогонаправленияспускаидлинышаговвыбираютсяэвристическиилипо
некоторойсхеме, котораяориентируетсянакакую-товнутреннююмодель, ноне
всегдаоптимальнымобразом. Такимобразом, появляетсярискненайтиулучшения
накаком-либошаге. Однаконеудачимогутбытьизученыиповедениеметодаможет
изменитьсявсоответствиисполученнойинформацией. Такойхарактерповедения
алгоритмовпрямогопоискапослужилпричиной, покоторойзанимизакрепилось
общееназваниеметодов пробиошибок. Наразработкутакихметодовбыло
затраченомногоусилийинекоторыеизметодоввыдержалипроверкувременеми
являются эффективными процедурами, нашедшими широкое применение и
используемымидосихпор. Основноедостоинствоэтихметодов - нетеоретическое
доказательствосходимостиилискоростисходимости, апростотареализации,
доказанность их работоспособности на практике и отсутствие сложных
подготовительныхэтапов, вродеаналитическоговычисленияпервыхивторых
производных. Крометого, приоптимизациисложныхфункцийдалеконевсегда
возможноаналитическоеопределениепроизводных, неговоряужеоразрывных
функциях.
Вслучаежевыпуклойиликвадратичнойунимодальнойфункцииметоды
прямогопоискавобщемработаютхужеметодовпервогоивторогопорядка,
обсуждаемых
в
другом
разделе
.
