Powers D.L. Boundary Value Problems and Partial Differential Equations

Подождите немного. Документ загружается.

28 Chapter 0 Ordinary Differential Equations

Substituting the derivative for the slope and making some algebraic adjust-

ments, we obtain



(x + x) − u



(x)



=f (x )x.

Dividing through by x yields



(x +x) − u



(x)

x

=f (x).

In the limit, as x approaches 0, the difference quotient in the left member

becomes the second derivative of u, and the result is the equation

=f (x), (3)

which is valid for x in the range 0 < x < a, where the cable is located. In addi-

tion, u(x) must satisfy the boundary conditions

u(0) = h

, u(a) =h

. (4)

For any particular case, we must choose an appropriate model for the load-

ing, f (x). One possibility is that the cable is hanging under its own weight of

w units of weight per unit length of cable. Then in Eq. (2), we should put

f (x)x = w

s

x

x,

where s represents arc length along the cable. In the limit, as x approaches 0,

s/x has the limit

lim

x→0

s

x



1 +





Therefore, with this assumption, the boundary value problem that determines

the shape of the cable is



1 +





, 0 < x < a, (5)

u(0) = h

, u(a) =h

. (6)

Notice that the differential equation is nonlinear. Nevertheless, we can ﬁnd its

general solution in closed form and satisfy the boundary conditions by appro-

priate choice of the arbitrary constants that appear. (See Exercises 4 and 5.)

Another case arises when the cable supports a load uniformly distributed in

the horizontal direction, as given by

f (x )x = wx.

0.3 Boundary Value Problems 29

Figure 5 Cylinder of heat-conducting material.

This is approximately true for a suspension bridge. The boundary value prob-

lem to be solved is then

, 0 < x < a,

u(0) =h

, u(a) =h

. (7)

The general solution of the differential equation (7) can be found by the

procedures of Sections 1 and 2. It is

u(x) =





x +c

where c

and c

are arbitrary. The two boundary conditions require

u(0) =h

: c

u(a) =h





a +c

Thesetwoaresolvedforc

and c

in terms of given parameters. The result,

after some beautifying algebra, is

u(x) =



−ax



−h

x +h

. (8)

Clearly, this function speciﬁes the cable’s shape as part of a parabola opening

upward.



Example: Heat Conduction in a Rod.

A long rod of uniform material and cross section conducts heat along its axial

direction (see Fig. 5). We assume that the temperature in the rod, u(x),does

not change in time. A heat balance (“what goes in must come out”) applied to

a slice of the rod between x and x + x (Fig. 6) shows that the heat ﬂow rate

q, measured in units of heat per unit time per unit area, obeys the equation

q(x)A +g(x)A x = q(x + x)A, (9)

30 Chapter 0 Ordinary Differential Equations

Figure 6 Section cut from heat-conducting cylinder showing heat ﬂow.

in which A is the cross-sectional area and g is the rate at which heat enters the

slice by means other than conduction through the two faces. For instance, if

heat is generated in the slice by an electric current I, we might have

g(x)A x = I

R x, (10)

where R is the resistance of the rod per unit length. If heat is lost through

the cylindrical surface of the rod by convection to a surrounding medium at

temperature T,theng(x ) would be given by “Newton’s law of cooling,”

g(x)A x =−h(u(x) −T)C x, (11)

where C is the circumference of the rod and h is the heat transfer coefﬁcient.

(This minus sign appears because, if u(x)>T, heat actually leaves the rod.)

Equation (9) may be altered algebraically to read

q(x +x) −q(x)

x

=g(x),

and application of the limiting process leaves

=g(x). (12)

The unknown function u(x) does not appear in Eq. (12). However, a well-

known experimental law (Fourier’s law) says that the heat ﬂow rate through a

unit area of material is directly proportional to the temperature difference and

inversely proportional to thickness. In the limit, this law takes the form

q =−κ

. (13)

The minus sign expresses the fact that heat moves from hotter toward cooler

regions.

Combining Eqs. (12) and (13) gives the differential equation

−κ

=g(x), 0 < x < a, (14)

where a is the length of the rod and the conductivity κ is assumed to be con-

stant.

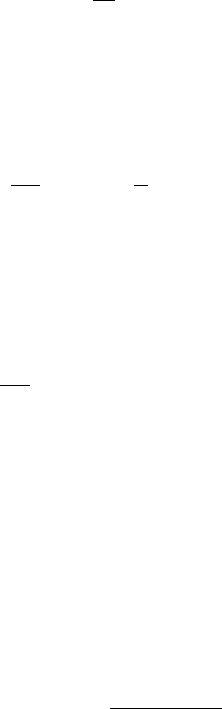
0.3 Boundary Value Problems 31

If the two ends of the rod are held at constant temperature, the boundary

conditions on u would be

u(0) =T

, u(a) =T

. (15)

On the other hand, if heat were supplied at x = 0 (by a heating coil, for in-

stance), the boundary condition there would be

−κA

(0) =H, (16)

where H is measured in units of heat per unit time.

Example.

Solve the problem

−κ

=−hu(x)

, 0 < x < a, (17)

u(0) =T

, u(a) =T

. (18)

(Physically, the rod is losing heat to a surrounding medium at temperature 0,

whilebothendsareheldatthesametemperatureT

.) If we designate µ

hC/κA, the differential equation becomes

−µ

u =0, 0 < x < a,

with general solution

u(x) = c

cosh(µx) +c

sinh(µx).

Application of the boundary condition at x = 0givesc

= T

; the second

boundary condition requires that

u(a) =T

: T

cosh(µa) +c

sinh(µa).

Thus c

(1 −cosh(µa))/ sinh(µa) and

u(x) = T



cosh(µx) +

1 −cosh(µa)

sinh(µa)

sinh(µx)





It should be clear now that solving a boundary value problem is not sub-

stantially different from solving an initial value problem. The procedure is (1)

ﬁnd the general solution of the differential equation, which must contain some

arbitrary constants, and (2) apply the boundary conditions to determine val-

ues for the arbitrary constants. In our examples the differential equations have

32 Chapter 0 Ordinary Differential Equations

Figure 7 Column carrying load P.

Figure 8 Section of column showing forces and moments.

been of second order, causing the appearance of two arbitrary constants, which

are to be determined by the boundary conditions.

The next example is somewhat different in spirit from the others. Instead of

just ﬁnding the solution of a boundary value problem, we will be looking for

parameter values that permit the existence of solutions of special form.

Example: Buckling of a Column.

A long, slender column whose bottom end is hinged carries an axial load as

shown in Fig. 7. The upper end of the column can move up or down but not

sideways. The displacement of the column’s centerline from a vertical reference

line is given by u(x).Ifthecolumnwerecutatanypointx, an upward force P

and a clockwise moment Pu(x) wouldhavetobeappliedtotheupperpartto

keep it in equilibrium (see Fig. 8). This force and moment must be supplied

by the lower part of the column.

0.3 Boundary Value Problems 33

It is known that the internal bending moment (positive when counterclock-

wise) in a column is given by the product

where E is Young’s modulus and I is the moment of inertia of the cross-

sectional area. (The moment I = b

/12 for a column whose cross section is

asquareofsideb .) Thus equating the external moment to the internal mo-

ment gives the differential equation

=−Pu, 0 < x < a, (19)

which, together with the boundary conditions

u(0) =0, u(a) = 0, (20)

determines the function u(x).

In order to study this problem more conveniently, we set

=λ

so that the differential equation becomes

+λ

u =0, 0 < x < a. (21)

Now, the general solution of this differential equation is

u(x) = c

cos(λx) + c

sin(λx).

As u(0) = 0, we must choose c

= 0, leaving u(x) = c

sin(λx). The second

boundary condition requires that

u(a) =0: c

sin(λa) = 0.

If sin(λa) is not 0, the only possibility is that c

= 0. In this case we ﬁnd that

the solution is

u(x) ≡ 0, 0 < x < a.

Physically, this means that the column stands straight and transmits the load

to its support, as it was probably intended to do.

Something quite different happens if sin(λa) = 0, for then any choice of

gives a solution. The physical manifestation of this case is that the column

assumes a sinusoidal shape and may then collapse, or buckle, under the axial

load. Mathematically, the condition sin(λa) = 0meansthatλa is an integer

34 Chapter 0 Ordinary Differential Equations

multiple of π,sincesin(π) = 0, sin(2π) = 0, etc., and integer multiples of π

are the only arguments for which the sine function is 0. The equation λa = π ,

in terms of the original parameters, is



a = π.

It is reasonable to think of E, I,anda as given quantities; thus it is the force

P = EI





called the critical or Euler load, that causes the buckling. The higher critical

loads, corresponding to λa = 2π , λa =3π , etc., are so unstable as to be of no

physical interest in this problem.



The buckling example is one instance of an eigenvalue problem. The gen-

eral setting is a homogeneous differential equation containing a parameter λ

and accompanied by homogeneous boundary conditions. Because both dif-

ferential equations and boundary conditions are homogeneous, the constant

function 0 is always a solution. The question to be answered is: What values

of the parameter λ allow the existence of nonzero solutions? Eigenvalue prob-

lems often are employed to ﬁnd the dividing line between stable and unstable

behavior. We will see them frequently in later chapters.

EXERCISES

1. Of these three boundary value problems, one has no solution, one has

exactly one solution, and one has an inﬁnite number of solutions. Which

is which?

+u = 0, u(0) =0, u(π) = 0;

+u = 1, u(0) =0, u(1) = 0;

+u = 0, u(0) =0, u(π) = 1.

2. Find the Euler buckling load of a steel column with a 2 in. × 3in.rectan-

gular cross section. The parameters are E = 30 × 10

lb/in.

, I = 2in.

a = 10 ft.

3. Find all values of the parameter λ for which these homogeneous boundary

value problems have a solution other than u(x) ≡ 0.

+λ

u =0, u(0) = 0,

(a) =0;

0.3 Boundary Value Problems 35

+λ

u =0,

(0) =0, u(a) = 0;

+λ

u =0,

(0) = 0,

(a) =0.

4. Verify, by differentiating and substituting, that

u(x) = c



cosh



µ(x + c)



is the general solution of the differential equation (5). (Here µ = w/T.

The graph of u(x) is called a catenary.)

5. Find the values of c and c



for which the function u(x) in Exercise 4 satisﬁes

the conditions

u(0) =h, u(a) = h.

6. A beam that is simply supported at its ends carries a distributed lateral

load of uniform intensity w (force/length) and an axial tension load T

(force). The displacement u(x) of its centerline (positive down) satisﬁes

the boundary value problem here. Find u(x).

−

u =−

Lx −x

, 0 < x < L,

u(0) =0, u(L) = 0.

7. The temperature u(x) in a cooling ﬁn satisﬁes the differential equation

κA

(u −T), 0 < x < a,

and boundary conditions

u(0) =T

, −κ

(a) =h



u(a) −T



That is, the temperature at the left end is held at T

> T while the surface

of the rod and its right end exchange heat with a surrounding medium at

temperature T.Findu(x).

8. Calculate the limit as a tends to inﬁnity of u(x), the solution of the prob-

lem in Exercise 7. Is the result physically reasonable?

9. In an electrical heating element, the temperature u(x) satisﬁes the bound-

ary value problem that follows. Find u(x).

κA

(u −T) −

κA

, 0 < x < a,

u(0) =T, u(a) =T.

36 Chapter 0 Ordinary Differential Equations

Figure 9 Poiseuille ﬂow.

10.

Verify that the solution of the problem given in Eqs. (17) and (18) can also

be written as follows, with µ

=Ch/Aκ:

u(x) = T

cosh(µ(x −a/2))

cosh(µa/2)

11. (Poiseuille ﬂow) A viscous ﬂuid ﬂows steadily between two large paral-

lel plates so that its velocity is parallel to the x-axis. (See Fig. 9.) The

x -component of velocity of the ﬂuid at any point (x, y) is a function of

y only. It can be shown that this component u(x) satisﬁes the differential

equation

=−

, 0 < y < L,

where µ is the viscosity and −g is a constant, negative pressure gradi-

ent. Find u(y), subject to the “no-slip” boundary conditions, u(0) = 0,

u(L) =0.

12. If the beam mentioned in Exercise 6 is subjected to axial compression in-

stead of tension, the boundary value problem for u(x) becomes the one

here. Solve for u(x).

u =−

Lx −x

, 0 < x < L,

u(0) = 0, u(L) = 0.

13. For what value(s) of the compressive load P in Exercise 12 does the prob-

lem have no solution or inﬁnitely many solutions?

14. The pressure p(x) in the lubricant under a plane pad bearing satisﬁes the

problem





=−K, a < x < b,

p(a) =0, p(b) = 0.

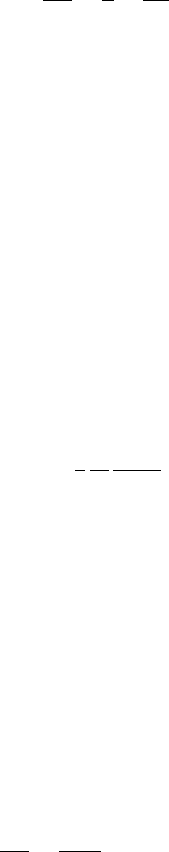
0.3 Boundary Value Problems 37

Find p(x) in terms of a, b,andK (constant). Hint: The differential equa-

tion can be solved by integration.

15. In a nuclear fuel rod, nuclear reaction constantly generates heat. If we treat

a rod as a one-dimensional object, the temperature u(x) in the rod might

satisfy the boundary value problem

κA

(u −T), 0 < x < a,

u(0) = T, u(a) = T.

Here, g is the heat generation rate or power density, and the terms on the

right-hand side represent heat transfer by convection to a surrounding

medium, usually pressurized water. Find u(x).

16. Sketch the solution of Exercise 15 and determine the maximum temper-

ature encountered. Typical values for the parameters are g = 300 W/cm

T = 325

◦

C, κ = 0.01 cal/cm s

◦

C, a = 2.9m,C/A = 4/cm, h =

0.035 cal/cm

◦

C. It will be useful to know that 1 W =0.239 cal/s.

17. An assembly of nuclear fuel rods is housed in a pressure vessel shaped

roughly like a cylinder with ﬂat or hemispherical ends. The temperature

in the thick steel wall of the vessel affects its strength and thus must be

studied for design and safety. Treating the vessel as a long cylinder (that

is, ignoring the effects of the ends), it is easy to derive this differential

equation in cylindrical coordinates for the temperature u(r) in the wall:

(rdu)

=0, a < r < b,

where a and b are the inner and outer radii, respectively. The boundary

conditions both involve convection, with hot pressurized water at the in-

ner radius and with air at the outer radius:

−κu



(a) = h



−u(a)



κu



(b) = h



−u(b)



Find u(r) in terms of the parameters, carefully checking the dimensions.

18. If a beam of uniform cross section is simply supported at its ends and

carries a distributed load w(x) along its length, then the displacement u(x)

of its centerline satisﬁes the boundary value problem

w(x)

, 0 < x < a,

u(0) = 0, u



(0) =0, u(a) = 0, u



(a) =0.