Powers D.L. Boundary Value Problems and Partial Differential Equations
Подождите немного. Документ загружается.


18 Chapter 0 Ordinary Differential Equations
Figure 2 Mass–spring–damper system with an external force.
from rest, with an external sinusoidal force (see Fig. 2) is described by this
initial value problem:
d
2
u
dt
2
+b
du
dt
+ω
2
u =f
0
cos(µt),
u(0) =0,
du
dt
(0) = 0.
See the Section 1 example on the mass–spring–damper system. The coeffi-
cient f
0
is proportional to the magnitude of the force. There are three impor-
tant cases.
b =0, µ = ω: undamped, no resonance. The form of the trial solution is
u
p
(t) = A cos(µt) +B sin(µt).
Substitution and simple algebra lead to the particular solution
u
0
(t) =
f
0
ω
2
−µ
2
cos(µt)
(that is, B = 0).Thegeneralsolutionofthedifferentialequationis
u(t) =
f
0
ω
2
−µ
2
cos(µt) + c
1
cos(ωt) +c
2
sin(ωt).
Applying the initial conditions determines c
1
and c
2
. Finally, the solution of
the initial value problem is
u(t) =
f
0
ω
2
−µ
2
cos(µt) −cos(ωt)
.

0.2 Nonhomogeneous Linear Equations 19
b = 0, µ = ω: resonance.
Now, since ω = µ, the trial solution must be
revised to
u
p
(t) = At cos(µt) +Bt sin(µt).
Substitution into the differential equation and simple algebra give A =0, B =
f
0
/2µ,or
u
p
(t) =
f
0
2µ
t sin(µt).
The general solution of the differential equation is
u(t) =
f
0
2µ
t sin(µt) +c
1
cos(µt) + c
2
sin(µt).
(Remember that b = 0andω = µ.) The initial conditions give c
1
= c
2
= 0, so
the solution of the initial value problem is
u(t) =
f
0
2µ
t sin(µt).
The presence of the multiplier t means that the amplitude of the oscillation is
increasing. This is the phenomenon of resonance.
b > 0: damped motion. The ideas are straightforward applications of the
techniques developed earlier. The trial solution is a combination of cos(µt)
and sin(µt).Somewhatlesssimplealgebragives
u
p
(t) =
f
0
(ω
2
−µ
2
) cos(µt) +µb sin(µt)
,
where = (ω
2
−µ
2
)
2
+µ
2
b
2
.Thegeneralsolutionofthedifferentialequation
may take different forms, depending on the relation between b and ω.(See
Section 1.) Assuming the underdamped case holds, we have
u(t) =
f
0
(ω
2
−µ
2
) cos(µt) +µb sin(µt)
+e
−bt/2
c
1
cos(γ t) + c
2
sin(γ t)
for the general solution of the differential equation. Here, γ =
ω
2
−(b/2)
2
is real because we assumed underdamping.
Applying the initial conditions gives, after some nasty algebra,
c
1
=−
f
0
ω
2
−µ
2
, c
2
=−
f
0
b
γ
ω
2
+µ
2
2
.

20 Chapter 0 Ordinary Differential Equations
Notice that, as t increases, the terms that come from the complementary
solution approach 0, while the terms that come from the particular solution
persist. These cases are illustrated with animation on the CD.
B. Variation of Parameters
Generally, if a linear homogeneous differential equation can be solved, the cor-
responding nonhomogeneous equation can also be solved, at least in terms of
integrals.
1. First-order equations
Suppose that u
c
(t) is a solution of the homogeneous equation
du
dt
=k(t)u. (5)
Then to find a particular solution of the nonhomogeneous equation
du
dt
=k(t)u +f (t), (6)
we assume that u
p
(t) = v(t)u
c
(t). Substituting u
p
in this form into the differ-
ential equation (6) we have
dv
dt
u
c
+v
du
c
dt
=k(t)vu
c
+f (t). (7)
However, u
c
= k(t)u
c
,soonetermontheleftcancelsatermontheright,
leaving
dv
dt
u
c
=f (t), or
dv
dt
=
f (t)
u
c
(t)
. (8)
The latter is a nonhomogeneous equation of simplest type, which can be
solved for v(t) in one integration.
Example.
Use this method to find a solution of the nonhomogeneous equation
du
dt
=5u +t.
We should try the form u
p
(t) = v(t) · e
5t
,becausee
5t
is a solution of u
= 5u.
Substituting the preceding form for u
p
,wefind
dv
dt
·e
5t
+v ·5e
5t
=5ve
5t
+t,
0.2 Nonhomogeneous Linear Equations 21
or, after canceling 5ve
5t
from both sides and simplifying, we find
dv
dt
=e
−5t
t.
This equation is integrated once (by parts) to find
v(t) =
−
t
5
−
1
25
e
−5t
.
From here, we obtain u
p
(t) = v(t) ·e
5t
=−
1
5
t +
1
25
.
2. Second-order equations
To find a particular solution of the nonhomogeneous second-order equation
d
2
u
dt
2
+k(t)
du
dt
+p(t)u = f (t), (9)
we need two independent solutions, u
1
(t) and u
2
(t),ofthecorrespondingho-
mogeneous equation
d
2
u
dt
2
+k(t)
du
dt
+p(t)u = 0. (10)
Then we assume that our particular solution has the form
u
p
(t) = v
1
(t)u
1
(t) +v
2
(t)u
2
(t), (11)
where v
1
and v
2
are functions to be found. If we simply insert u
p
in this form
intoEq.(9),weobtainonecomplicatedsecond-orderequationintwoun-
known functions. However, if we impose the extra requirement that
dv
1
dt
u
1
+
dv
2
dt
u
2
=0, (12)
then we find that
u
p
= v
1
u
1
+v
2
u
2
+v
1
u
1
+v
2
u
2
=v
1
u
1
+v
2
u
2
, (13)
u
p
= v
1
u
1
+v
2
u
2
+v
1
u
1
+v
2
u
2
, (14)
and the equation that results from substituting Eq. (11) into Eq. (9) becomes
v
1
u
1
+v
2
u
2
+v
1
(u
1
+k(t)u
1
+p(t)u
1
) +v
2
(u
2
+k(t)u
2
+p(t)u
2
) =f (t).
This simplifies further: The multipliers of v
1
and v
2
are both 0, because u
1
and
u
2
satisfy the homogeneous Eq. (10).

22 Chapter 0 Ordinary Differential Equations
Thus, we are left with a pair of simultaneous equations,
v
1
u
1
+v
2
u
2
=0, (12
)
v
1
u
1
+v
2
u
2
=f (t), (15)
in the unknowns v
1
and v
2
. The determinant of this system is
u
1
u
2
u
1
u
2
=W(t), (16)
the Wronskian of u
1
and u
2
. Since these were to be independent solutions of
Eq. (10), their Wronskian is nonzero, and we may solve for v
1
(t) and v
2
(t) and
hence for v
1
and v
2
.
Example.
Use variation of parameters to solve the nonhomogeneous equation
d
2
u
dt
2
+u = cos(ωt).
Assume a solution in the form
u
p
(t) = v
1
cos(t) + v
2
sin(t),
because sin(t) and cos(t) are independent solutions of the corresponding ho-
mogeneous equation u
+u = 0. The assumption of Eq. (12) is
v
1
cos(t) + v
2
sin(t) = 0. (17)
Then our equation reduces to the following, corresponding to Eq. (15):
−v
1
sin(t) +v
2
cos(t) = cos(ωt). (18)
Now we solve Eqs. (17) and (18) simultaneously to find
v
1
=−sin(t) cos(ωt), v
2
=cos(t) cos(ωt). (19)
Theseequationsaretobeintegratedtofindv
1
and v
2
,andthenu
p
(t).
Finally, we note that v
1
(t) and v
2
(t) can be found from Eqs. (12) and (15)
in general:
v
1
=−
u
2
f
W
,v
2
=
u
1
f
W
. (20)
Integrating these two equations, we find that
v
1
(t) =−
u
2
(t)f (t)
W(t)
dt,v
2
(t) =
u
1
(t)f (t)
W(t)
dt. (21)

0.2 Nonhomogeneous Linear Equations 23
Now, Eq. (11) may be used to form a particular solution of the nonhomoge-
neous equation (9).
We may a lso o bta in v
1
and v
2
by using definite integrals with variable upper
limit:
v
1
(t) =−
t
t
0
u
2
(z)f (z)
W(z)
dz,v
2
(t) =
t
t
0
u
1
(z)f (z)
W(z)
dz. (22)
Thelowerlimitisusuallytheinitialvalueoft,butmaybeanyconvenient
value. The particular solution can now be written as
u
p
(t) =−u
1
(t)
t
t
0
u
2
(z)f (z)
W(z)
dz +u
2
(t)
t
t
0
u
1
(z)f (z)
W(z)
dz.
Furthermore, the factors u
1
(t) and u
2
(t) can be inside the integrals (which are
not with respect to t), and these can be combined to give a tidy formula, as
follows.
Theorem 3. Let u
1
(t) and u
2
(t) be independent solutions of
d
2
u
dt
2
+k(t)
du
dt
+p(t)u = 0(H)
with Wronskian W(t) = u
1
(t)u
2
(t) −u
2
(t)u
1
(t).Then
u
p
(t) =
t
t
0
G(t, z)f (z) dz
is a particular solution of the nonhomogeneous equation
d
2
u
dt
2
+k(t)
du
dt
+p(t)u = f (t), (NH)
where G is the Green’s function defined by
G(t, z) =
u
1
(z)u
2
(t) −u
2
(z)u
1
(t)
W(z)
. (23)
EXERCISES
In Exercises 1–10, find the general solution of the differential equation.

24 Chapter 0 Ordinary Differential Equations
1.
du
dt
+a(u − T) = 0.
3.
du
dt
+au = e
−at
.
5.
d
2
u
dt
2
+u = cos(t).
7.
d
2
u
dt
2
+3
du
dt
+2u = cosh(t).
9.
1
ρ
2
d
dρ
ρ
2
du
dρ
=−1.
2.
du
dt
+au = e
at
.
4.
d
2
u
dt
2
+u = cos(ωt)(ω=1).
6.
d
2
u
dx
2
−γ
2
(u −U) = 0
(U,γ
2
are constants).
8.
1
r
d
dr
r
du
dr
=−1.
10.
d
2
u
dt
2
=−1.
11. Let h(t) be the height of a parachutist above the surface of the earth. Con-
sideration of forces on his body leads to the initial value problem for h:
M
d
2
h
dt
2
+K
dh
dt
=−Mg,
h(0) =h
0
,
dh
dt
(0) = 0
(M = mass, g = acceleration of gravity, K = parachute constant). Solve
the problem, taking g = 32 ft/s
2
and K/M = 0.1/s.
12. Solve this initial value problem for forced vibrations,
d
2
u
dt
2
+ω
2
u =f
0
sin(µt),
u(0) =0,
du
dt
(0) = 0,
in two cases: (a) µ = ω,(b)µ = ω.
In Exercises 13–19, use variation of parameters to find a particular solution of
the differential equation. Be sure that the differential equation is in the correct
form.
13.
du
dt
+au = e
−at
, u
c
(t) = e
−at
.
14. t
du
dt
=−1, u
c
(t) = 1.
15.
d
2
y
dx
2
+y =tan(x), y
1
(x) = cos(x), y
2
(x) = sin(x).
16.
d
2
y
dx
2
+y =sin(x), y
1
(x) = cos(x), y
2
(x) = sin(x).
0.2 Nonhomogeneous Linear Equations 25
17.
d
2
u
dt
2
=−1, u
1
(t) = 1, u
2
(t) = t.
18.
1
r
d
dr
r
du
dr
=−1, u
1
(r) = 1, u
2
(r) = ln(r).
19. t
2
d
2
u
dt
2
+t
du
dt
−u = 1, u
1
(t) = t, u
2
(t) =
1
t
.
In Exercises 20–22, use Theorem 3 to develop the formula shown for a partic-
ular solution of the differential equation.
20.
d
2
u
dt
2
+γ
2
u =f (t), u
p
(t) =
1
γ
t
0
sin
γ(t − z)
f (z) dz.
21.
du
dt
+au = f (t), u
p
(t) =
t
0
e
−a(t−z)
f (z) dz.
22.
d
2
u
dt
2
−γ
2
u =f (t), u
p
(t) =
1
γ
t
0
sinh
γ(t − z)
f (z) dz.
23. In “Model for temperature estimation of electric couplings suffering heavy
lightning currents” [A.D. Polykriti et al., IEE Proceedings — Generation,
Transmission and Distribution, 151 (2004): 90–94], the authors model the
temperature rise above ambient in a coupling with this initial value prob-
lem:
ρc
dT
dt
=i
2
(t)R(1 +αT), T(0) = 0.
Parameters: ρ is density, c is specific heat, i(t) is the current due to a light-
ening strike, R is the resistance of the coupling at ambient temperature,
and the factor (1 +αT) shows how resistance increases with temperature.
Simplify the differential equation algebraically to get
dT
dt
=Ki
2
(t)(β +T), T(0) = 0,
and identify β and K in terms of the other parameters.
24. (Continuation) The authors model the lightning current with the func-
tion i(t) = I
max
(e
−λt
− e
−µt
)/n,wheren is a factor to make I
max
the ac-
tual maximum. Obtain graphs of this function and the simpler function
i(t) = I
max
e
−λt
, using these values: I
max
= 100 kA, n = 0.93, λ = 2.1,
µ = 150. The unit for time is milliseconds. Graph for t from 0 to 2 ms,
which is the range of interest.
25. (Continuation) Solve the initial value problem using the simpler function
for current. (Don’t forget to square.) Graph the result for t from 0 to 2 ms,
using β = 0.26 and K = 13.

26 Chapter 0 Ordinary Differential Equations
0.3 Boundary Value Problems
A boundary value problem in one dimension is an ordinary differential equa-
tion together with conditions involving values of the solution and/or its deriv-
atives at two or more points. The number of conditions imposed is equal to
the order of the differential equation. Usually, boundary value problems of any
physical relevance have these characteristics: (1) The conditions are imposed
at two different points; (2) the solution is of interest only between those two
points; and (3) the independent variable is a space variable, which we shall
represent as x. In addition, we are primarily concerned with cases where the
differential equation is linear and of second order. However, problems in elas-
ticity often involve fourth-order equations.
In contrast to initial value problems, even the most innocent looking
boundary value problem may have exactly one solution, no solution, or an
infinite number of solutions. Exercise 1 illustrates these cases.
When the differential equation in a boundary value problem has a known
general solution, we use the two boundary conditions to supply two equations
that are to be satisfied by the two constants in the general solution. If the dif-
ferential equation is linear, these are two linear equations and can be easily
solved, if there is a solution.
In the rest of this section we examine some physical examples that are natu-
rally associated with boundary value problems.
Example: Hanging Cable.
First we consider the problem of finding the shape of a cable that is fastened
at each end and carries a distributed load. The cables of a suspension bridge
provide an important example. Let u(x) denote the position of the centerline
of the cable, measured upward from the x-axis, which we assume to be hori-
zontal. (See Fig. 3.) Our objective is to find the function u(x).
The shape of the cable is determined by the forces acting on it. In our analy-
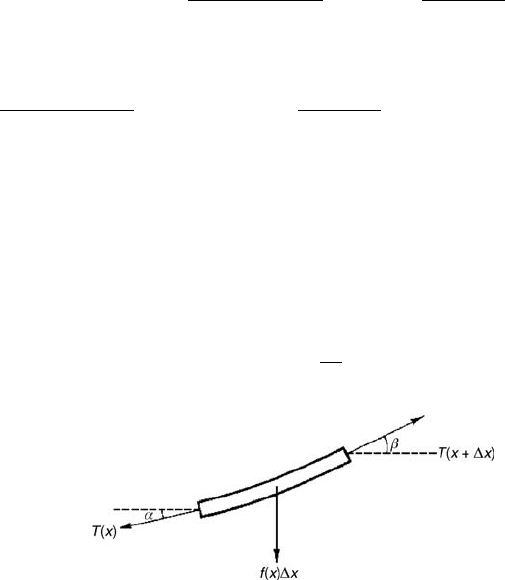
sis, we consider the forces that hold a small segment of the cable in place. (See
Fig. 4.) The key assumption is that the cable is perfectly flexible. This means
that force inside the cable is always a tension and that its direction at every
point is the direction tangent to the centerline.
Figure 3 The hanging cable.
0.3 Boundary Value Problems 27
We suppose that the cable is not moving. Then by Newton’s second law,
the sum of the horizontal components of the forces on the segment is 0, and
likewise for the vertical components. If T(x) and T(x+x) are the magnitudes
of the tensions at the ends on the segment, we have these two equations:
T(x + x) cos
φ(x + x)
−T(x) cos
φ(x)
=0 (Horizontal), (1)
T(x + x) sin
φ(x + x)
−T(x) sin
φ(x)
−f (x)x = 0 (Ve r t i c a l ). (2)
In the second equation, f (x) is the intensity of the distributed load, measured
in force per unit of horizontal length, so f (x)x is the load borne by the small
segment.
From Eq. (1) we see that the horizontal component of the tension is the same
at both ends of the segment. In fact, the horizontal component of tension has
the same value — call it T — at every point, including the endpoints where
the cable is attached to solid supports. By simple algebra we can now find the
tension in the cable at the ends of our segment,
T(x + x) =
T
cos
φ(x + x)
, T(x) =
T
cos
φ(x)
,
and substitute these into Eq. (2), which becomes
T
cos
φ(x + x)
sin
φ(x + x)
−
T
cos
φ(x)
sin
φ(x)
−f (x)x = 0
or
T
tan
φ(x + x)
−tan
φ(x)
−f (x)x = 0.
Before going further we should note (Fig. 4) that φ(x) measures the angle
between the tangent to the centerline of the cable and the horizontal. As the
position of the centerline is given by u(x),tan(φ(x)) is just the slope of the
cable at x. From elementary calculus we know
tan
φ(x)
=
du
dx
(x).
Figure 4 Section of cable showing forces acting on it. The angles are α = φ(x),
β =φ(x +x).
