Powers D.L. Boundary Value Problems and Partial Differential Equations

Подождите немного. Документ загружается.

338 Chapter 5 Higher Dimensions and Other Coordinates

(x) = 1

(x) = x

(x) = (3x

−1)/2

(x) = (5x

−3x)/2

(x) = (35x

−30x

+3)/8

Tab le 3 Legendre polynomials

Figure 12 Graphs of the ﬁrst ﬁve Legendre polynomials.

index are also zero. Hence, one of the solutions of



1 −x





−2xy



+12y =0

is the polynomial a

(x − 5x

/3).Theothersolutionisanevenfunctionun-

bounded at both x =±1.

Now we see that the boundedness conditions can be satisﬁed only if µ

one of the numbers 0, 2, 6,...,n(n + 1),.... In such a case, one solution of

the differential equation is a polynomial (naturally bounded at x =±1). When

normalized by the condition y(1) = 1, these are called Legendre polynomials,

written P

(x). Table 3 provides the ﬁrst ﬁve Legendre polynomials. Figure 12

shows their graphs.

5.9 Spherical Coordinates; Legendre Polynomials 339

Since the differential equation (5) is easily put into self-adjoint form,



(1 −x







+µ

y = 0, −1 < x < 1,

it is routine to show that the Legendre polynomials satisfy the orthogonality

relation



−1

(x)P

(x) dx = 0, n = m.

By direct calculation, it can be shown that



−1

(x) dx =

2n +1

. (6)

A compact way of representing the Legendre polynomials is by means of Ro-

drigues’ formula,

(x) =

n!2



−1)



. (7)

Elementary algebra and calculus show that the nth derivative of (x

− 1)

apolynomialofdegreen. Substituting this polynomial into the differential

equation (5), with µ

= n(n + 1), shows that it is a solution — bounded, of

course. Therefore, it is a multiple of the Legendre polynomial P

(x).Through

Rodrigues’ formula or otherwise, it is possible to prove the following two for-

mulas, which relate three consecutive Legendre polynomials:

(2n +1)P

(x) = P



n+1

(x) −P



n−1

(x), (8)

(n +1)P

n+1

(x) +nP

n−1

(x) = (2n +1)xP

(x). (9)

In order to use Legendre polynomials in boundary value problems, we need

to be able to express a given function f (x) in the form of a Legendre series,

f (x ) =

∞



n=0

(x), −1 < x < 1.

From the orthogonality relation and the integral, Eq. (6), it follows that the

coefﬁcient in the series must be

2n +1



−1

f (x)P

(x) dx. (10)

The convergence theorem for Legendre series is analogous to the one for

Fourier series in Chapter 1.

340 Chapter 5 Higher Dimensions and Other Coordinates

Theorem. If f (x) is sectionally smooth on the interval −1 < x < 1,thenatevery

point of that interval the Legendre series of f is convergent, and

∞



n=0

(x) =

f (x+) +f (x−)



From Eq. (10) for the coefﬁcient of a Legendre series and from the fact that

the Legendre polynomials are odd or even, we see that an odd function will

have only odd-indexed coefﬁcients that are nonzero, and an even function will

have only even-indexed coefﬁcients that are nonzero. Furthermore, if a func-

tion f isgivenontheinterval0< x < 1, then its odd and even extensions have

odd and even Legendre series, and f is represented by either in that interval:

f (x) =



n even

(x), 0 < x < 1,

= (2n +1)



f (x)P

(x) dx (n even), (11)

f (x) =



n odd

(x), 0 < x < 1,

= (2n +1)



f (x)P

(x) dx (n odd). (12)

Because the P

(x) are polynomials, the integral equation (10) for any spe-

ciﬁc coefﬁcient can be done in closed form for a variety of functions f (x).

However, getting a

as a function of n is not so easy. Fortunately, some ele-

mentary integrals can be done using the differential equation



(1 −x







+n(n + 1)P

=0.

(1) First, separate the two terms of the differential equation and integrate:

n(n +1)



(x) dx =



−



(1 −x







=−



1 −x





(x).

This equation may be solved for the integral if n =0.

(2) Now multiply through the differential equation by x, separate terms, and

integrate:

n(n +1)



(x) dx =



−x



(1 −x







=−x



1 −x









1 −x





=−x



1 −x





1 −x



−



(−2x)P

dx.

5.9 Spherical Coordinates; Legendre Polynomials 341

Next, move the last term to the left-hand member of the equation to ﬁnd

(n +2)(n −1)



(x) dx =



1 −x



(x) −xP



(x)



This equation can be solved for the integral on the left, provided that n = 1.

(For n = 1, the integration is done directly.)

Summary



(x) dx =

−(1 −x

)

n(n +1)



(x), (13)



(x) dx =

(1 −x

)

(n +2)(n −1)



(x) −xP



(x)



(14)

These integration formulas are useful if we can evaluate P

(x) and P



(x)

easily for any x. The relations in Eqs. (8) and (9) are useful for this purpose.

We illustrate by ﬁnding P

(0).First,notethatP

(0) = 0 for odd values of n,

because the Legendre polynomials with odd index are odd functions of x.For

odd n,Eq.(9)gives

(n +1)P

n+1

(0) +nP

n−1

(0) =0,

n+1

(0) =−

n +1

n−1

(0).

Because P

(0) =1, we ﬁnd successively that

(0) =−

, P

(0) =

1 ·3

2 ·4

, P

(0) =−

1 ·3 ·5

2 ·4 ·6

or in general

(0) = (−1)

n/2

1 ·3 ···(n −1)

2 ·4 ···n

, n = 2, 4, 6,...

(0) = 0, n = 1, 3, 5,....

(15)

Similarly, but not as easily, Eq. (8) can be used to ﬁnd the values of P



(0).It

is simpler to use the relation



(0) =nP

n−1

(0), (16)

which can be derived from Eqs. (8) and (9).

342 Chapter 5 Higher Dimensions and Other Coordinates

Example.

Let

f (x ) =



−1, −1 < x < 0,

1, 0 < x < 1.

The Legendre series will contain only odd-indexed polynomials, and their co-

efﬁcients are

= (2n +1)



(x) dx (n odd)

=−

2n +1

n(n +1)



1 −x





(x)



2n +1

n(n +1)



(0) =

2n +1

n +1

n−1

(0)

= (−1)

(n−1)/2

1 ·3 ·5 ···(n −2)

2 ·4 ·6 ···(n −1)

2n +1

n +1

(n =3, 5, 7,...).

Speciﬁcally we ﬁnd b

= 3/2 (by a separate calculation), b

=−7/8, b

11/16,....Becausef (x) is indeed sectionally smooth,

f (x) =

(x) −

(x) +

(x) −···.

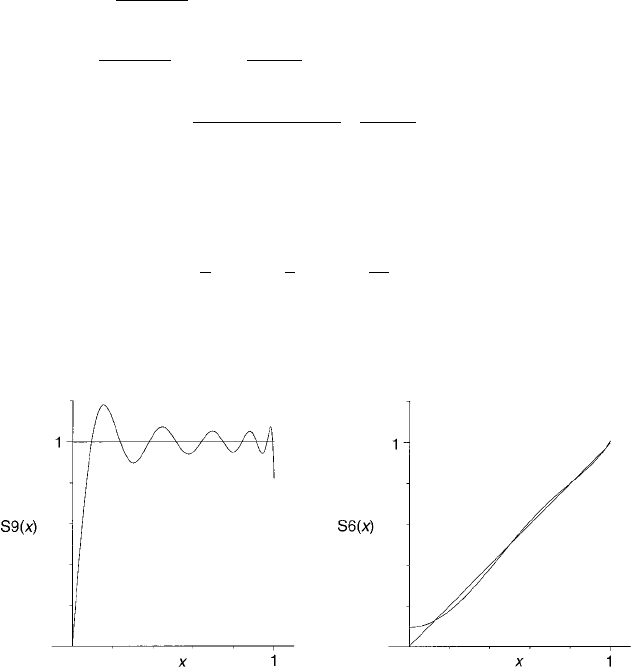
See Fig. 13 for graphs of the partial sums of this series.



(a) (b)

Figure 13 Graphs of a function and a partial sum of its Legendre series:

(a) through P

(x) for the function f (x) in the example; (b) through P

(x) for

f (x) =|x|, −1 < x < 1. Compare with the partial sums of the Fourier series, Figs. 9

and10ofChapter1.

5.9 Spherical Coordinates; Legendre Polynomials 343

Figure 14 The nodal curves of the zonal harmonics are the parallels

(φ = constant) on a sphere, where P

(cos(φ)) = 0. The nodal curves are shown

in projection for n = 1, 2, 3, 4. See the CD for color versions.

Summary

The solution of the eigenvalue problem



(1 −x







+µ

y = 0, −1 < x < 1,

y(x) bounded at x =−1andatx =1,

is y (x) =P

(x), µ

=n(n +1), n = 0, 1, 2,....

The solution of the eigenvalue problem



sin(φ)







+µ

sin(φ) = 0,

(φ) bounded at φ =0andatφ =π,

is (φ) =P

(cos(φ)), µ

=n(n +1), n = 0, 1, 2,....

TheLegendrepolynomialsP

(cos(φ)) are often called zonal harmonics be-

cause their nodal lines (loci of solutions of P

(cos(φ)) = 0) divide a sphere

into zones, as shown in Fig. 14.

EXERCISES

1. Equation (4) may be solved by assuming

(φ) =

∞



cos(kφ).

Find the relations among the coefﬁcients a

by computing the terms of the

equation in the form of series. Use the identities

sin(φ) sin(kφ) =



cos



(k −1)φ



−cos



(k +1)φ



sin(φ) cos(kφ) =−



sin



(k −1)φ



+sin



(k +1)φ



344 Chapter 5 Higher Dimensions and Other Coordinates

Show that the coefﬁcients are all zero after a

if µ

=n(n +1).

2. Derive the formula for the coefﬁcients b

, as shown in Eq. (10).

3. Find P

(x), ﬁrst from the formulas for the a’s and second by using Eq. (9)

with n = 4.

4. Verify Eqs. (6) and (7) for n = 0, 1, 2 and Eq. (9) for n =2, 3.

5. One of the solutions of (1 − x



− 2xy



= 0isy(x) = 1(µ

= 0).Find

another independent solution of this differential equation.

6. Show that the orthogonality relation for the eigenfunctions 

(φ) =

(cos(φ)) is





(φ)

(φ) sin(φ) dφ = 0, n = m.

7. Obtain the relation



n+1

(x) = (n +1)P

(x) +xP



(x)

by differentiating Eq. (9) and eliminating P



n−1

between that and Eq. (8).

Note that Eq. (16) follows from this relation.

8. Let F =(x

−1)

. Show that F satisﬁes the differential equation



−1





=2nxF.

9. Differentiate both sides of the preceding equation n+1 times to show that

the nth derivative of F satisﬁes Legendre’s equation (5). Use Leibniz’s rule

for derivatives of a product.

10. Obtain Eq. (6) by these manipulations:

a. Multiply through Eq. (9) by P

n+1

,integratefrom−1to1,andusethe

orthogonality of P

n+1

with P

n−1

b. Replace (2n + 1)P

by means of Eq. (8).

c. P

n+1

is orthogonal to xP



n−1

, which is a polynomial of degree n.

d. Solve what remains for the desired integral.

11. Find the Legendre series for the function f (x) =|x|, −1 < x < 1.

12. Find the Legendre series for the following function. Note that f (x ) −1/2

is an odd function.

f (x) =



0, −1 < x < 0,

1, 0 < x < 1.

5.10 Some Applications of Legendre Polynomials 345

5.10 Some Applications of Legendre

Polynomials

In this section we follow through the details involved in solving some problems

in which Legendre polynomials are used. First, we complete the problem stated

in the previous section.

A. Potential in a Sphere

We consider the axially symmetric potential equation — that is, with no vari-

ationinthelongitudinal-orθ-direction. The unknown function u might rep-

resent an electrostatic potential, steady-state temperature, etc.



∂

∂ρ



∂u

∂ρ



sin(φ)

∂

∂φ



sin(φ)

∂u

∂φ



=0,

0 <ρ<c, 0 <φ<π, (1)

u(c,φ)=f (φ), 0 <φ<π. (2)

Of course, the function u is to be bounded at the singular points φ = 0, φ =π ,

and ρ = 0. The assumption that u has the product form, u(ρ, φ) = (φ)R(ρ),

allows us to transform the partial differential equation into

(ρ



(r))



R(r)

(sin(φ)



(φ))



sin(φ)(φ)

=0.

FromhereweobtainequationsforR and  individually,







−µ

R =0, 0 <ρ<c, (3)



sin(φ)







+µ

sin(φ) = 0, 0 <φ<π. (4)

In Section 5.9 we found the eigenfunctions of Eq. (4), subject to the bound-

edness conditions at φ = 0andπ ,tobe

(φ) = P

(cos(φ)), corresponding

to the eigenvalues µ

= n(n + 1). We must still solve Eq. (3) for R.Afterthe

differentiation has been carried out, the problem for R becomes



+2ρR



−n(n + 1)R

=0, 0 <ρ<c,

bounded at ρ =0.

The equation is of the Cauchy–Euler type, solved by assuming R = ρ

and

determining α. Two solutions, ρ

and ρ

−(n+1)

, are found, of which the sec-

ond is unbounded at ρ =0. Hence R

= ρ

, and our product solutions of the

potential equation have the form

(ρ, φ) = R

(ρ)

(φ) = ρ



cos(φ)



346 Chapter 5 Higher Dimensions and Other Coordinates

The general solution of the partial differential equation that is bounded in the

region 0 <ρ<c,0<φ<π is thus the linear combination

u(ρ, φ) =

∞



n=0



cos(φ)



. (5)

At ρ = c, the boundary condition becomes

u(c,φ)=

∞



n=0



cos(φ)



=f (φ), 0 <φ<π. (6)

The coefﬁcients b

are then found to be

2n +1



f (φ)P



cos(φ)



sin(φ) dφ. (7)

B. Heat Equation on a Spherical Shell

The temperature on a spherical shell satisﬁes the three-dimensional heat equa-

tion. If initially there is no dependence on θ , then there will never be such de-

pendence. Furthermore, if the shell is thin (thickness much less than average

radius R), we may also assume that temperature does not vary in the radial

direction. The heat equation then becomes one-dimensional:

sin(φ)

∂

∂φ



sin(φ)

∂u

∂φ



∂u

∂t

, 0 <φ<π, 0 < t, (8)

u(φ, 0) = f (φ), 0 <φ<π. (9)

Naturally, we require boundedness of u at φ =0andφ = π .

The assumption of a product form for the solution, u(φ, t) = (φ)T(t),

leads to the conclusion that

(sin(φ)



(φ))



sin((φ))



(t)

kT(t)

=−µ

Thus, we have the eigenvalue problem



sin(φ)







+µ

sin(φ) = 0, 0 <φ<π,

(0) and (π) bounded.

The solution of this problem was found in Section 5.9 to be µ

=n(n +1) and



(φ) = P



cos(φ)



, n =0, 1, 2,....

Obviously, the other factor in a product solution must be

(t) = exp



−n(n +1)kt/R



5.10 Some Applications of Legendre Polynomials 347

Now, a series of constant multiples of product solutions is the most general

solution of our problem:

u(φ, t) =

∞



n=0



cos(φ)



−n(n+1)kt/R

. (10)

The initial condition, Eq. (9), now takes the form of a Legendre series,

∞



n=0



cos(φ)



=f (φ), 0 <φ<π. (11)

From the information in Section 5.9, we know that the coefﬁcients b

must be

chosen to be

2n +1





cos(φ)



f (φ) sin(φ) dφ.

Then if f (φ) is sectionally smooth for 0 <φ<π, the series of Eq. (11) actually

equals f (φ), and thus the function u(φ, t) in Eq. (10) satisﬁes the problem

originally posed.

For instance, if f (φ) = T

in the northern hemisphere (0 <φ<π/2) and

f (φ) =−T

in the southern (π/2 <φ<π), then the coefﬁcients are

2n +1



f (φ)P



cos(φ)



sin(φ) dφ

2n +1





−1



cos

−1

(x)



(x) dx



= T

2n +1

n +1

n−1

(0),

as found in the previous section. Figure 15 shows graphs of u(φ, t) as a func-

tion of φ in the interval 0 <φ<π for various times. The CD shows an ani-

mated version of the solution.

C. Spherical Waves

In Section 5.8, we solved the wave equation in spherical coordinates for the

case where the initial conditions depend only on the radial variable ρ.Nowwe

consider the case where the variable φ is also present. A full statement of the