Поттосин Ю.В. Дискретная математика и теория проектирования цифровых устройств и систем
Подождите немного. Документ загружается.

171
Два перехода q
i
→ q
j
и q
k
→ q
l
, совершаемые автоматом при одном и том
же входном сигнале в различные состояния (q
j
≠ q
l
), назовем парой переходов.
Тогда условие отсутствия опасных состязаний формулируется следующим
образом.
У т в е р ж д е н и е 22.1. При одновременном возбуждении элементов
памяти в процессе перехода опасные состязания отсутствуют тогда и только
тогда, когда для каждой пары переходов q
i
→ q
j
, q
k
→ q
l
имеет место
U(q
i
, q
j
) ∩ U(q
k
, q
l
) = ∅.
Множества U(q
i
, q
j
) и U(q
k
, q
l
) можно формально представить как
множества кодов соответствующих состояний, а те, в свою очередь,
представляются троичными векторами, полученными из кодов состояний q
i
, q
j
,
q
k
и q
l
. Обозначим эти векторы t(q
i
, q
j
) и t(q
k
, q
l
). Компоненты вектора t(q
i
, q
j
)
принимают значения одноименных компонент кодов q
i
и q
j
, если они
совпадают, и принимают значение «–» в противном случае. Например, если
коды состояний q
i
и q
j
соответственно (0 0 0 1) и (0 1 0 1), то t(q
i
, q
j
) = (0 – 0 1).
Необходимым и достаточным условием непересечения множеств U(q
i
, q
j
) и
U(q
k
, q
l
) является ортогональность векторов t(q
i
, q
j
) и t(q
k
, q
l
). К этому условию
надо добавить еще необходимое требование того, что для реализации
различных состояний их коды должны быть ортогональными.
Для автомата, таблицей переходов которого является табл. 22.1, имеются
следующие пары переходов:
для а
1
для а
3
q
1
→ q
1
, q
4
→ q
5
; q
1
→ q
4
, q
2
→ q
2
;
q
1
→ q
1
, q
5
→ q
5
; q
1
→ q
4
, q
5
→ q
2
;
q
2
→ q
1
, q
4
→ q
5
; q
2
→ q
2
, q
4
→ q
4
;
q
2
→ q
1
, q
5
→ q
5
; q
4
→ q
4
, q
5
→ q
2
.
q
3
→ q
1
, q
4
→ q
5
;
q
3
→ q
1
, q
5
→ q
5
;
Для входного сигнала а
2
пары переходов согласно определению этого
понятия отсутствуют. Легко проверить, что кодирование состояний,
представленное следующей матрицей, обеспечивает отсутствие опасных
состязаний:
C =
5
4
3
2
1
321
1
0
1
0
1
1
0
1
1
0
0
0
q
q
q
q
q
zzz
−
−
−
.
172
Функции возбуждения элементов памяти, описывающие сигналы, которые
устанавливают элементы памяти в нужные состояния, при фиксированных
значениях двоичных входных сигналов определяются на интервалах, которым
соответствуют множества U(q
i
, q
j
). Для любого U(q
i
, q
j
) такой интервал
представляется троичным вектором t(q
i
, q
j
). Пусть, например, коды состояний
автомата, поведение которого описывается с помощью табл. 22.1, представлены
приведенной выше матрицей С. Для кодирования входных сигналов
используются переменные х
1
, х
2
, значениями которых являются соответственно
0, 0 для а
1
, 0, 1 – для а
2
и 1, 0 – для а
3
. Тогда булевы функции, описывающие
рассматриваемый автомат, можно задать следующими матрицами, в которых
удалены строки, соответствующие поглощаемым интервалам:
U =
−
−
−
−
−
−
−
−
−
−
−
1
0
1
0
0
0
1
0
0
1
1
0
0
0
32121
zzzxx
, V =
−
−
−
+++
0
1
1
0
1
1
0
0
1
0
1
0
321
zzz
.
22.3. Минимизация длины кода
Кодирование состояний, обеспечивающее отсутствие опасных состязаний
(гонок), называется противогоночным. Естественно, здесь возникает задача
минимизации длины кода состояния, приводящая к наименьшему числу
элементов памяти в реальной схеме.
Условия отсутствия опасных состязаний можно выразить троичной
матрицей, в которой столбцы соответствуют состояниям автомата и для каждой
пары переходов q
i
→ q
j
, q
k
→ q
l
имеется хотя бы одна строка, где компоненты i
и j имеют одно значение, 0 или 1, а компоненты k и l – противоположное ему
значение. Остальные компоненты имеют значение «–». Эта матрица может
быть избыточна, если некоторые строки находятся в отношении импликации.
Троичный вектор a имплицирует троичный вектор b, если b получается из
a заменой некоторых нулей или единиц значением «–» и, возможно,
инвертированием полученного результата. Например, вектор (1 0 – – 1 0 1)
имплицирует (1 0 – – – 0 1) и (0 1 – – – 1 –). Смысл этого отношения в том, что
условие, представленное вектором b, автоматически выполняется при
соблюдении условия, представленного вектором a. Данное отношение обладает
свойствами рефлексивности и транзитивности.
Представим все условия отсутствия опасных состязаний в виде троичной
матрицы, удалим из нее имплицируемые строки и назовем полученную
матрицу матрицей условий.
173
Для автомата, таблицей переходов которого является табл. 22.1, условия
отсутствия опасных состязаний, определяемых парами переходов q
1
→ q
1
,
q
4
→ q
5
; q
1
→ q
1
, q
5
→ q
5
и q
2
→ q
1
, q
4
→ q
5
, могут быть представлены
следующими строками:
q
1
q
2
q
3
q
4
q
5
0 – – 1 1
0 – – – 1
0 0 – 1 1.
Здесь только последняя строка останется в матрице условий. Остальные строки
имплицируются последней строкой и в матрицу условий не включаются.
Будем говорить, что троичная матрица R имплицирует троичную матрицу
S, если для каждой строки матрицы S в матрице R найдется имплицирующая ее
строка.
Задача противогоночного кодирования сводится к нахождению матрицы с
минимальным числом строк, имплицирующей матрицу условий. Столбцы этой
матрицы будут представлять искомые коды состояний, т. е., чтобы получить
матрицу кодирования С, надо транспонировать кратчайшую имплицирующую
форму матрицы условий.
Множество строк матрицы условий называется совместимым, если
существует вектор, имплицирующий каждую строку этого множества. Заметим,
что множество строк, в котором каждая пара строк является совместимой, не
всегда является совместимым множеством. Действительно, пусть имеется три
троичных вектора: и = (0 1 – – 0 1), v = (– 1 0 – 0 –) и w = (– –1 – – 1). Для и и v
общим имплицирующим вектором является (0 1 0 – 0 1), для и и w – вектор
(0 1 1 – 0 1), а для v и w – вектор (– 0 1 – 1 1). Любой имплицирующий вектор
для двух векторов не является таковым для третьего. Совместимое множество
называется максимальным, если оно не является собственным подмножеством
другого совместимого множества.
Чтобы получить кратчайшую имплицирующую форму для троичной
матрицы, надо найти все максимальные совместимые множества ее строк, а
затем получить кратчайшее покрытие строк этими множествами.
Пусть табл. 22.2 представляет таблицу переходов заданного асинхронного
автомата. Для того чтобы учесть требование ортогональности кодов для
различных состояний, можно ввести в таблицу переходов еще один столбец,
где присутствуют все состояния, которые являются устойчивыми. Тогда
выполнение данного требования обеспечивается введением в матрицу условий
строк, не имплицируемых другими строками и выражающих отсутствие
опасных состязаний, которые соответствуют данному столбцу. При этом
табл. 22.2 примет вид табл. 22.3. Заметим, что неортогональные коды могут
оказаться у состояний, которым соответствуют одинаковые строки таблицы
переходов, и введение дополнительного столбца делает все строки различными.
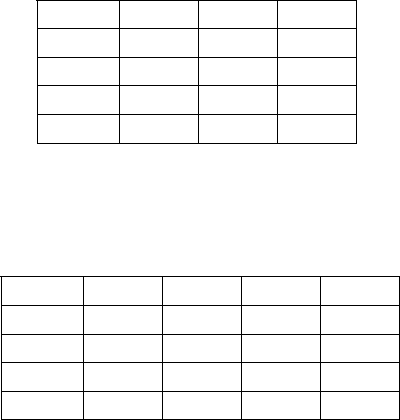
Таблица 22.2
174
Таблица переходов асинхронного автомата
а
1
а
2
а
3
а
4
q
1
q
1
q
1
q
1
q
5
q
2
q
1
q
2
q
2
q
2
q
3
q
3
q
2
q
4
q
5
q
4
q
3
q
2
q
4
q
5
q
5
– q
5
q
4
q
5
Таблица 22.3
Таблица переходов с дополнительным столбцом
а
1
а
2
а
3
а
4
а
5
q
1
q
1
q
1
q
1
q
5
q
1
q
2
q
1
q
2
q
2
q
2
q
2
q
3
q
3
q
2
q
4
q
5
q
3
q
4
q
3
q
2
q
4
q
5
q
4
q
5
– q
5
q
4
q
5
q
5
Анализируя табл. 22.3, нетрудно найти, в частности, что условия
отсутствия опасных состязаний при входном сигнала а
1
выражаются
следующими тироичными векторами (справа показаны рассматриваемые при
этом пары переходов)
q
1
q
2
q
3
q
4
q
5
0 – 1 – – q
1
→ q
1
, q
3
→ q
3
;
0 0 1 – – q
2
→ q
1
, q
3
→ q
3
;
0 – 1 1 – q
1
→ q
1
, q
4
→ q
3
;
0 0 1 1 – q
2
→ q
1
, q
4
→ q
3
.
В данном случае строка (0 0 1 1 –) имплицирует каждую из трех
остальных, которые, следовательно, не надо включать в матрицу условий.
Рассматривая остальные пары переходов и формируя для них соответствующие
троичные векторы, получим следующую матрицу условий, которая для
удобства обозрения разбита на секции, соответствующие различным столбцам
табл. 22.3:
175
S =
}
}
5
4
3
2
1
54321
10
9
8
7
6
5
4
3
2
1
1
0
1
1
1
1
1
1
1
0
1
1
0
1
0
1
1
0
1
0
0
0
1
1
0
0
0
0
0
0
a
a
a
a
a
qqqqq
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
.
Каждому совместимому множеству строк троичной матрицы согласно его
определению соответствует вектор, имплицирующий все строки, являющиеся
элементами этого множества. Для данной троичной матрицы S получим
следующие максимальные совместимые множества и соответствующие им
векторы:
{1, 6, 7, 9} (0 0 1 1 1);
{2, 3, 4, 5, 8} (0 1 1 1 0);
{2, 3, 6} (0 1 1 1 1);
{2, 4, 7, 8, 10} (0 1 1 0 0);
{3, 5, 8, 9, 10} (0 1 0 1 0);
{3, 6, 10} (0 1 0 1 1);
{4, 6, 7, 10} (0 0 0 1 1);
{7, 8, 9} (0 1 0 0 0).
Кратчайшее покрытие множества строк матрицы S составляют множества
{1, 6, 7, 9}, {2, 3, 4, 5, 8} и {2, 4, 7, 8, 10}. Соответствующие им векторы
являются вектор-столбцами матрицы кодирования заданного асинхронного
автомата:
C =
5
4
3
2
1
321
0
0
1
1
0
0
1
1
1
0
1
1
1
0
0
q
q
q
q
q
zzz
.
176
Литература
1. Ангер С. Асинхронные последовательностные схемы. – М.: Наука,
1977. – 400 с.
2. Ахо А., Хопкрофт Дж., Ульман Дж. Построение и анализ
вычислительных алгоритмов. – М.: Мир, 1979.
3. Баранов С.И. Синтез микропрограммных автоматов. – Л.: Энергия,
1979. – 232 с.
4. Вавилов Е.Н., Портной Г.П. Синтез схем электронных цифровых
машин. – М.: Советское радио, 1964. - 440 с.
5. Глушков В.М. Синтез цифровых автоматов. – М.: ГИФМЛ, 1962. – 476 с.
6. Закревский А.Д. Логический синтез каскадных схем. – М.: Наука. 1981. –
414 с.
7. Закревский А.Д., Поттосин Ю.В., Черемисинова Л.Д. Основы
логического проектирования. В 3 кн. Кн.1. Комбинаторные алгоритмы
дискретной математики. – Мн.: ОИПИ НАН Беларуси, 2004. – 226 с.
8. Закревский А.Д., Поттосин Ю.В., Черемисинова Л.Д. Основы
логического проектирования. В 3 кн. Кн.2. Оптимизация в булевом
пространстве. – Мн.: ОИПИ НАН Беларуси, 2004. – 240 с.
9. Закревский А.Д., Поттосин Ю.В., Черемисинова Л.Д. Основы
логического проектирования. В 3 кн. Кн.3. Проектирование устройств
логического управления. – Мн.: ОИПИ НАН Беларуси, 2006. – 254 с.
10. Зыков А.А. Основы теории графов. – М.: Наука, 1987.
11. Кристофидес Н. Теория графов. Алгоритмический подход. – М.: Мир,
1978. – 432 с.
12. Кузнецов О.П., Адельсон-Вельский Г.М. Дискретная математика для
инженеров. – М.: Энергия, 1988. – 480 с.
13. Лазарев В.Г., Пийль Е.И. Синтез управляющих автоматов. – М.:
Энергоатомиздат, 1989. – 328 с.
14. Лекции по теории графов / Емеличев В.А., Мельников О.И.,
Сарванов В.И., Тышкевич Р.И. – М.: Наука, 1990. – 384 с.
15. Миллер Р. Теория переключательных схем, т.I. – М.: Наука, 1970. –
416 с.
16. Миллер Р. Теория переключательных схем, т.II. – М.: Наука, 1971. –
304 с.
17. Поспелов Д.А. Логические методы анализа и синтеза схем. – М.; Л.:
Энергия, 1964. – 320 с.
18. Скляров В.А. Синтез автоматов на матричных БИС. – Минск: Наука и
техника, 1984. – 287 с.
19. Фридман А., Менон П. Теория и проектирование переключательных
схем. – М.: Мир, 1978. – 580 с.
20. Яблонский С.В. Введение в дискретную математику. – М.: Наука,
1986. – 384 с.
177
Предметный указатель
Автомат асинхронный 137
– конечный 136
– Мили 136
– Мура 136
– не полностью определенный 137
– полностью определенный 137
– синхронный 137
– частичный 137
алгебра булева 56
− логики 55
алгоритм жадный 38
антисимметричность 20
антиядро 98
аргумент 18
– существенный 54
– фиктивный 54
ассоциативность 12
Базис 72
булево пространство 52
булевы переменные 52
Вектор булев 52
– троичный 53
вершина графа 22
высказывание 60
Гиперкуб 66
граф 22
− бихроматический 39
− двудольный 24
− неориентированный 22
− ориентированный 22
– поведения автомата 138
− полный 23
группировка 150
– правильная 150
– – минимальная 150
Декартово произведение 15
дерево поиска 44
дизъюнкция 55
– с исключением 55
– элементарная 64
дистрибутивность 12
дихотомия 20
ДНФ (дизъюнктивная нормальная форма)
62
− безызбыточная 86
– кратчайшая 90
– минимальная 90
− совершенная 63
– сокращенная 90
дополнение графа 23
− множества 11
дуга графа 22
Закон двойного отрицания 57
− поглощения 57
− простого склеивания 57
законы де Моргана 57
значение функции 18
Импликанта 90
– простая 90
импликация 55
– формальная 86
инверсия 54
интервал булева пространства 53
– максимальный 90
– обязательный 94
Карта декомпозиции 115
– Карно 68
класс эквивалентности 20
КНФ (конъюнктивная нормальная форма)
64
код Грея 69
коммутативность 12
композиция отношений 17
компонента (связности) 27
конституента единицы 64
− нуля 65
корень дерева 44
контур 27
конъюнкция полная 62
– элементарная 62
кратчайшая имплицирующая форма 173
178
Литерал 62
Матрица булева 15
− инцидентности 26
– программируемая логическая (ПЛМ) 75
− различий 111
− смежности 25
– совместимости 152
– троичная 53
– − вырожденная 79
– условий 173
метод Блейка–Порецкого 95
– Квайна–МакКласки 90
минор 80
множество 8
– интервально поглощаемое 108
– – – максимальное 108
− независимое 30
− − максимальное 30
− − наибольшее 30
– непосредственно производное 150
− пустое 8
– совместимое 154
– характеристическое 52
мощность множества 9
мультиграф 27
Область значений функции 16
– определения функции 16
объединение множеств 11
окрестность вершины 23
отношение 15
− бинарное 15
− взаимно однозначное 18
– между матрицами 78
– – – – импликации 173
– – – – эквивалентности 78
– между векторами 77
– – – ортогональности 77
– – – пересечения 77
– – – поглощения 77
– – – смежности 77
– – – соседства 77
– реализации между булевыми функциями
106
Пара переходов 171
пересечение множеств 11
петля 23
подграф 26
− остовный 26
− полный 35
− порожденный 27
подмножество 8
− несобственное 8
покрытие 46
− кратчайшее 46
− столбцовое 111
полнота системы функций 72
полный перебор 42
порядок 20
− лексикографический 21
правила редукции 49, 81
принцип двойственности 13
противогоночное кодирование 172
Равносильность формул 11
размерность булева пространства 52
ранг интервала 67
– конъюнкции 62
раскраска графа 36
расстояние в графе 27
ребро графа 22
редукционный метод 80
рефлексивность 20
Сечение 16
симметричность 20
склеивание 13
– обобщенное 14
− простое 13
совместимость 20
– состояний 152
– строк матрицы условий 173
соответствие 15
состояние автомата 136
состязания 170
сравнимость 53
степень множества 15
– вершины 23
сумма множеств 11
– по модулю два 55
суперпозиция функций 55
179
схема комбинационная 135
Таблица выходов 138
– истинности 52
– переходов 138
– – и выходов 138
транзитивность 20
Факторизация 47.4 396
формула 55
функция 18
– булева 52
– – не полностью определенная 54
– – полностью определенная 54
– – слабо определенная 108
– – частичная 54
− возбуждения 172
− всюду определенная 18
– выходов 136
– переходов 136
Цепь 27
− порождаемая парой состояний 145
цикл 27
Число доминирования 29
− независимости 30
− хроматическое 36
Эквивалентность состояний 144
эквивалентные матрицы 78
эквиваленция 55
элемент определяющий 94
Ядро 98
180
