Поттосин Ю.В. Дискретная математика и теория проектирования цифровых устройств и систем
Подождите немного. Документ загружается.

131
Как видно, выполнение операции 3 уменьшает число единиц в строках
матрицы Х
′
. Операции 2 и 3 повторяются до тех пор, пока в каждой строке
матрицы Х
′
число единиц будет не более чем k.
4. Для i-й строки матрицы Х
′
в получаемую систему уравнений вносится
уравнение K
i
=
p
iii
zzz ∧∧∧ ...
21
(i = 1, 2, … , т), где т – число строк матрицы
Х
′
,
j
i
z (j = 1, 2, … , p) – литерал, соответствующий столбцу, с единицей в i-й
строке матрицы Х
′
, р – число единиц в i-й строке матрицы Х
′
.
В результате выполнения описанных действий получим систему
уравнений, описывающую ту часть синтезируемой схемы, которая реализует
элементарные конъюнкции из заданной системы ДНФ.
17.2. Реализация дизъюнкций
Для реализации дизъюнкций выполняются следующие действия, в
основном подобные тем действиям, которые выполнялись при реализации
конъюнкций.
1. Путем транспонирования матрицы Y получается матрица Y
′
.
2. В матрице Y
′
отыскивается минор, содержащий только единицы и
образованный не более чем k столбцами и как можно большим числом строк.
3. Все единицы матрицы Y
′
, входящие в полученный минор, заменяются
нулями, в матрицу Y
′
добавляется столбец g
j
+ 1
, где j – число столбцов, которое
к данному моменту приобрела матрица Y
′
в результате выполнения
рассматриваемых действий. Этот столбец имеет единицы в строках минора и
нули – в остальных строках. В формируемую систему уравнений вносится
уравнение g
j
+ 1
=
p
iii
zzz ∨∨∨ ...
21
, где
j
i
z (j = 1, 2, … , p) – литерал,
соответствующий столбцу, входящему в выделенный минор.
Так же, как в предыдущем процессе, операции 2 и 3 повторяются до тех
пор, пока в каждой строке матрицы Y
′
число единиц будет не более чем k.
4. Для i-й строки матрицы Y
′
в получаемую систему уравнений вносится
уравнение у
i
=
p
iii
zzz ∨∨∨ ...
21
(i = 1, 2, … , т), где т – число строк матрицы
Y
′
,
j
i
z
(j = 1, 2, … , p) – литерал, соответствующий столбцу, с единицей в i-й
строке матрицы Y
′
, р – число единиц в i-й строке матрицы Y
′
.
В результате выполнения описанных действий получим систему
уравнений, описывающую ту часть синтезируемой схемы, которая реализует
дизъюнкции.

132
17.3. Пример
Для демонстрации описанного метода зададим базис элементов с числом
входных полюсов 2 и возьмем в качестве примера систему ДНФ, заданную
следующей парой матриц:
Х =
−
−
−
− 0
0
1
1
0
0
0
0
1
1
0
0
1
1
1
1
0
0
1
0
4321
xxxx
, Y =
6
5
4
3
2
1
0
0
1
1
0
1
0
1
0
1
1
0
1
0
0
1
0
1
321
yyy
.
В результате преобразования матрицы Х получим следующую матрицу:
Х
′
=
1
0
1
0
0
0
0
0
0
1
1
0
1
1
1
1
0
0
0
0
0
0
1
1
1
1
0
0
0
0
0
0
1
0
1
1
0
0
1
1
0
1
0
1
0
0
1
0
4
4
3
3
2
2
1
1
xxxxxxxx
.
В этой матрице замечаем минор, образованный строками 1, 2 и столбцами
х
1
, х
2
. Выполняя пункты 2 и 3 процесса реализации конъюнкций, получаем
следующие матрицу и уравнение:
Х
′
=
0
0
0
0
1
1
1
0
1
0
0
0
0
0
0
1
1
0
1
1
1
1
0
0
0
0
0
0
0
0
1
1
0
0
0
0
0
0
1
0
0
0
0
0
1
1
0
1
0
1
0
0
1
0
1
4
4
3
3
2
2
1
1
gxxxxxxxx
, g
1
= x
2
x
3
.
Повторяя те же действия, получаем следующие матрицы и уравнения:

133
Х
′
=
0
0
1
1
0
0
0
0
0
0
1
1
1
0
1
0
0
0
0
0
0
1
1
0
1
1
0
0
0
0
0
0
0
0
0
0
1
1
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
1
0
1
0
0
1
0
21
4
4
3
3
2
2
1
1
ggxxxxxxxx
, g
2
=
x
1
x
3
;
Х
′
=
1
1
0
0
0
0
0
0
1
1
0
0
0
0
0
0
1
1
1
0
1
0
0
0
0
0
0
1
1
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
1
0
1
0
0
1
0
321
4
4
3
3
2
2
1
1
gggxxxxxxxx
, g
3
=
x
2
x
3
;
Х
′
=
0
0
0
0
1
0
1
1
0
0
0
0
0
0
1
1
0
0
0
0
0
0
1
1
1
0
1
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
1
0
1
0
0
0
0
4321
4
4
3
3
2
2
1
1
ggggxxxxxxxx
, g
4
= x
1
x
4
;
Х
′
=
0
0
1
0
0
0
0
0
0
0
1
0
1
1
0
0
0
0
0
0
1
1
0
0
0
0
0
0
1
1
1
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
1
0
1
0
0
0
0
54321
4
4
3
3
2
2
1
1
gggggxxxxxxxx
, g
5
=
x
2
x
4
.
В последней матрице все строки имеют ровно по две единицы. Им
соответствуют уравнения K
1
=
x
1
g
1
, K
2
= g
1
g
4
, K
3
= x
4
g
2
, K
4
= g
2
g
5
, K
5
= x
1
g
3
,
K
6
=
x
4
g
3
.
134
Результатом транспонирования матрицы Y является матрица
Y
′
=
3
2
1
654321
0
0
1
0
1
0
1
0
0
1
1
1
0
1
0
1
0
1
y
y
y
KKKKKK
.
Эта матрица имеет только один минор с единицами, содержащий более
одной строки. Он образован строками у
1
, у
3
и столбцами K
1
, K
3
. Для
уменьшения числа единиц в строке у
2
берем однострочный минор со столбцами
K
2
, K
3
. В результате получаем следующую матрицу и соответствующие
уравнения:
Y
′
=
3
2
1
76654321
0
1
0
1
0
1
0
0
1
0
1
0
1
0
0
0
0
0
0
0
0
0
0
0
y
y
y
ggKKKKKK
, g
6
= K
1
∨ K
2
, g
7
= K
2
∨ K
3
.
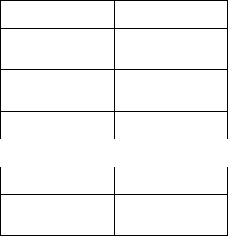
Полное описание схемы представляется следующей системой уравнений:
g
1
= x
2
x
3
; g
5
=
x
2
x
4
; K
4
= g
2
g
5
; g
6
= K
2
∨ K
3
;
g
2
=
x
1
x
3
; K
1
=
x
1
g
1
; K
5
= x
1
g
3
; у
1
= K
6
∨ g
6
;
g
3
=
x
2
x
3
; K
2
= g
1
g
4
; K
6
=
x
4
g
3
; у
2
= K
5
∨ g
7
;
g
4
=
x
1
x
4
; K
3
= x
4
g
2
; g
6
= K
1
∨ K
2
; у
3
= K
4
∨ g
6
.
135
Г л а в а 18
Конечный автомат. Типы
18.1. Автомат с памятью
До сих пор рассматривались устройства, не обладающие памятью. Такие
устройства в любой момент времени на любую комбинацию входных двоичных
сигналов реагируют однозначно, т. е. каждой комбинации двоичных сигналов
на входе устройства соответствует определенная комбинация двоичных
сигналов на выходе независимо от того, какие сигналы приходили на вход
раньше. Отсюда происходят названия «комбинационный автомат» или
«комбинационная схема».
Общепринятой моделью поведения такого устройства является система
булевых функций. Комбинации двоичных сигналов иногда удобно обозначать
абстрактными символами или буквами некоторого заданного алфавита. Пусть
имеется входной алфавит А = {a
1
, a
2
, … , a
α
} и выходной алфавит
В = {b
1
, b
2
, … , b
β
}. Тогда общий вид описания поведения комбинационного
автомата можно представить табл. 18.1, где
j
i
b ∈ В. Эта таблица является
аналогом таблицы истинности. Она полностью определяет алгоритм
функционирования заданного устройства.
Таблица 18.1
Пример задания комбинационного автомата
Вход Выход
а
1
1
i
b
а
2
2
i
b
… …
а
α
α
i
b
Часто алгоритм функционирования устройства бывает таким, что простым
соответствием вида табл. 18.1 его задать невозможно. Для его описания
необходимо ввести время, и работа устройства рассматривается во времени.
Время носит дискретный характер, т. е. течение времени представляется как
последовательность моментов. В любой момент времени устройство принимает
сигнал на входе и выдает сигнал на выходе. В различные моменты устройство
может реагировать на один и тот же входной сигнал по-разному. Пусть,
например, на вход устройства с входным и выходным алфавитами
А = {a
1
, a
2
, а
3
, a
4
} и В = {b
1
, b
2
, b
3
} пришла последовательность сигналов
a
1
a
1
а
3
a
2
a
2
а
4
a
3
,
136
а на выходе наблюдается последовательность сигналов
b
2
b
3
b
2
b
1
b
3
b
2
b
1
.
В первый момент времени устройство на входной сигнал а
1
реагировало
выходным сигналом b
2
, а во второй момент на тот же сигнал – сигналом b
3
. На
сигналы а
2
и а
3
в разные моменты оно реагировало также по-разному, т. е.
поведение устройства нельзя описать тем же способом, что использовался для
описания поведения комбинационного автомата.
Эта неоднозначность устраняется, если ввести понятие внутреннего
состояния или просто состояния. Тогда то, что устройство реагирует на один и
тот же сигнал в разные моменты по-разному, можно объяснить так, что оно
находится при этом в разных состояниях. Приняв входной сигнал, устройство
выдает выходной сигнал и может перейти в другое состояние.
Состояния образуют множество Q = {q
1
, q
2
, … , q
γ
}. Тогда алгоритм
функционирования устройства можно представить совокупностью строк вида
(a
i
, q
j
) → (q
s
, b
t
),
где a
i
∈ А, b
t
∈ В, q
j
, q
s
∈ Q. Устройство, поведение которого можно задать в
таком виде, носит название «автомат с памятью» или
«последовательностный автомат». Последний термин заключает в себе смысл
отображения входной последовательности в другую.
Соответствие (a
i
, q
j
) → (q
s
, b
t
) можно задать таблицей, подобной табл. 18.1,
где фактически представлены две функции, определенные на множестве A × Q.
Областью значений одной функции является множество Q, другой функции –
множество В.
Моделью описанного устройства является конечный автомат,
представляющий собой совокупность следующих объектов:
А = {a
1
, a
2
, … , a
α
} – множество входных символов, или входной алфавит;
В = {b
1
, b
2
, … , b
β
} – множество выходных символов, или выходной
алфавит;
Q = {q
1
, q
2
, … , q
γ
} – множество состояний, или внутренний алфавит;
Ψ : A × Q → Q – функция переходов;
Φ : A × Q → В – функция выходов.
Для конечного автомата используется обозначение (A, B, Q, Ψ, Φ). Слово
«конечный» подчеркивает, что все три множества, входящие в состав данной
модели, конечны. В том виде, в каком эта модель здесь представлена, она носит
название «автомат Мили». Другой разновидностью данной модели является
автомат Мура, отличающийся от автомата Мили только тем, что функция
выходов не зависит от входного символа, т. е. представляет собой отображение
Φ : Q → В.
137
Значением функции Ψ(a, q) является состояние q
+
, в которое переходит
автомат из состояния q, если на вход его подан символ а. Значением функции
Φ(a, q) является выходной символ, выдаваемый автоматом в состоянии q при
поступлении на его вход символа а, а значением функции Φ(q) автомата Мура –
выходной символ b, который выдает автомат, находясь в состоянии q. Если
значения функций Ψ(a, q) и Φ(a, q) определены для любой пары значений
аргументов а и q, а в модели Мура функция Φ(q) определена для всех значений
q, то автомат является полностью определенным, или полным автоматом. Иногда
приходится иметь дело с не полностью определенным, или частичным
автоматом, у которого эти функции могут быть определены не везде.
Конечный автомат является абстрактной математической моделью
дискретного устройства. Поведение, описанное данной моделью, может быть
по-разному реализовано в дискретном устройстве. При синхронной реализации
моменты времени, когда определяется состояние, в которое переходит
устройство, а в случае автомата Мили и выходной символ, зафиксированы.
Технически это осуществляется введением генератора синхронизирующих
сигналов, которые инициируют соответствующие действия. Период следования
таких сигналов не должен быть меньше чем время, необходимое для
завершения переходных процессов в устройстве. Реализованный таким образом
конечный автомат называется синхронным автоматом.
При асинхронной реализации указанные моменты времени не
фиксированы. Они связаны с моментами, в которые происходит изменение
входного сигнала. Реализованный таким образом автомат называется
асинхронным автоматом. Если синхронный автомат различает
последовательности разной длины из одинаковых входных символов, т. е.
может реагировать на них различными выходными последовательностями, то
асинхронный автомат воспринимает последовательность одинаковых входных
символов любой длины как один символ. В схеме такого устройства генератор
синхронизирующих сигналов отсутствует.
В асинхронном автомате переход из состояния в состояние происходит за
некоторый конечный промежуток времени, в течение которого не должен
меняться входной сигнал. При действии любого входного сигнала автомат
приходит в некоторое устойчивое состояние, из которого он не выходит до
конца действия данного сигнала. При этом должно выполняться требование
прямого перехода, которое формально выражается следующим образом: если
Ψ(a, q
i
) = q
j
, то Ψ(a, q
j
) = q
j
. Иногда допускается выполнение следующей
цепочки переходов: Ψ(a, q
i
) = q
r
, Ψ(a, q
r
) = q
s
, … , Ψ(a, q
t
) = q
j
, Ψ(a, q
j
) = q
j
.
18.2. Представления автомата
Конечный автомат удобно представлять таблицей переходов и таблицей
выходов. Строкам этих таблиц соответствуют состояния автомата, столбцам –
входные символы. На пересечении строки, соответствующей состоянию q, и

138
столбца, соответствующего входному символу а, в таблице переходов
записывается значение Ψ(a, q), а в таблице выходов – значение Φ(a, q).
Другими словами, в первом случае в клетке таблицы указывается состояние, в
которое автомат переходит из состояния q при поступлении на его вход
символа а, а во втором случае – выходной символ, который при этом выдает
автомат. Табл.18.2 и табл.18.3 представляют собой пример описанного
представления автомата Мили, у которого А = {a
1
, a
2
, a
3
, a
4
}, В = {b
1
, b
2
} и
Q = {q
1
, q
2
, q
3
}.
Таблица 18.2 Таблица 18.3
Функция Ψ Функция Φ
a
1
a
2
a
3
a
4
a
1
a
2
a
3
a
4
q
1
q
1
q
2
q
1
q
2
q
1
b
1
b
1
b
2
b
1
q
2
q
3
q
1
q
3
q
1
q
2
b
1
b
2
b
2
b
1
q
3
q
3
q
1
q
1
q
1
q
3
b
2
b
2
b
1
b
1
Зная начальное состояние автомата и входную последовательность,
нетрудно получить по этим таблицам соответствующую последовательность
выходных символов. Приведем пример такого соответствия для автомата,
заданного табл. 18.2 и 18.3, на вход которого поступила последовательность
символов а
1
, а
2
, а
2
, а
1
, а
3
, а
4
, а
1
, а
4
при начальном состоянии q
1
. Покажем также
состояния, которые проходит автомат:
а
1
а
2
а
2
а
1
а
3
а
4
а
1
а
4
q
1
q
1
q
2
q
1
q
1
q
1
q
2
q
3
b
1
b
1
b
2
b
1
b
2
b
1
b
1
b
1
.
Автомат Мура представляется одной таблицей переходов, к которой
добавлен один столбец со значениями функции выходов (табл. 18.4).
Можно свести таблицу переходов и таблицу выходов автомата Мили в
одну таблицу, которую называют таблицей переходов и выходов. Такая таблица
для автомата, заданного в виде табл. 18.2 и табл. 18.3, имеет вид табл. 18.5.
Более наглядным при небольшом числе состояний является представление
автомата в виде графа поведения автомата, который представляет собой
ориентированный граф. Его вершины соответствуют состояниям автомата, а
дуги – переходам между состояниями. При этом дуга помечается всеми
входными символами, которые вызывают соответствующий переход, и
выходными символами, сопровождающими данный переход (в случае автомата
Мили). В случае автомата Мура выходными символами помечаются вершины,
соответствующие состояниям, в которых находится автомат при выдаче данных
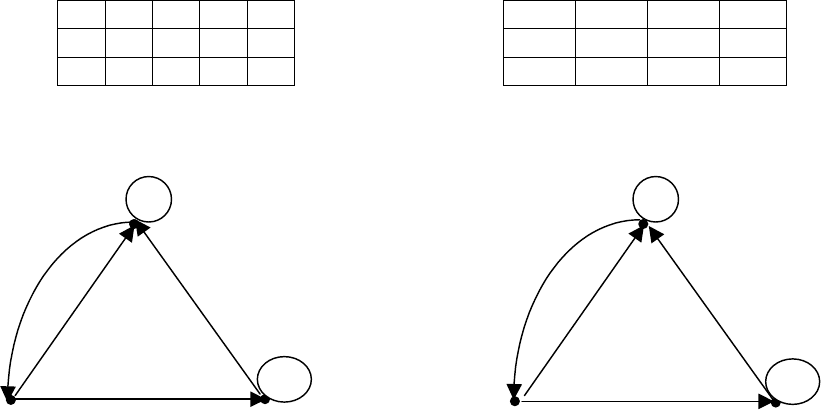
символов. На рис. 18.1 изображены графы переходов автоматов, заданных
табл. 18.4 и 18.5.
139
Таблица 18.4 Таблица 18.5
Таблица переходов автомата Мура Таблица переходов и выходов
автомата Мили
a
1
a
2
a
3
a
4
Φ
a
1
a
2
a
3
a
4
q
1
q
1
q
2
q
1
q
2
b
1
q
1
q
1
,b
1
q
2
,b
1
q
1
,b
2
q
2
,b
1
q
2
q
3
q
1
q
3
q
1
b
1
q
2
q
3
,b
1
q
1
,b
2
q
3
,b
2
q
1
,b
1
q
3
q
3
q
1
q
1
q
1
b
2
q
3
q
3
,b
2
q
1
,b
2
q
1
,b
1
q
1
,b
1
a
1
, a
3
a
1
/b
1
, a
3
/b
2
q
1
, b
1
a
2
/b
1
, a
4
/b
1
q
1
a
2
/b
2
, a
3
/b
1
, a
4
/b
1
a
2
, a
4
a
2
, a
3
, a
4
a
2
, a
4
a
2
/b
2
, a
4
/b
1
a
1
/b
2
a
1
q
2
, b
1
a
1
, а
3
q
3
, b
2
q
2
a
1
/b
1
, а
3
/b
2
q
3
а) б)
Рис. 18.1. Примеры графов поведения: а) автомата Мура; б) автомата Мили
Еще одним способом представления автомата является матрица
поведения, представляющая собой квадратную матрицу, строки и столбцы
которой помечаются состояниями автомата. В случае автомата Мура на
пересечении строки q
i
и столбца q
j
матрицы поведения записываются входные
символы, переводящие автомат из состояния q
i
в состояние q
j
, а строки
помечаются также и выходными символами. В случае автомата Мили элементы
матрицы поведения, кроме входных символов, вызывающих соответствующие
переходы, содержат выходные символы, которые сопровождают эти переходы.
Если из состояния q
i
нет перехода в состояние q
j
, то на пересечении строки q
i
и
столбца q
j
ставится прочерк. Для рассмотренных автоматов ниже представлены
матрицы поведения, причем первая из них – матрица поведения автомата Мура,
вторая – матрица поведения автомата Мили.
−
−
−
1
1
42
432
42
31
23
12
11
321
,
,,
,
,
,
,
,
a
a
aa
aaa
aq
aa
bq
bq
bq
qqq
,

140
−
−
−
21
11
1412
141332
1422
2311
3
2
1
321
/
/
/ ,/
/ ,/ ,/
/ ,/
/ ,/
ba
ba
baba
bababa
baba
baba
q
q
q
qqq
.
18.3. Связь между моделями Мили и Мура
Всякое отображение входных последовательностей в выходные может
быть реализовано как с помощью модели Мили, так и с помощью модели Мура.
Определим преобразование, переводящее любой автомат Мили в
эквивалентный ему автомат Мура, а также преобразование, переводящее любой
автомат Мура в эквивалентный ему автомат Мили.
Пусть задан автомат Мура М = (A, B, Q, Ψ, Φ) и требуется получить
эквивалентный ему автомат Мили М
∗
= (A
∗
, B
∗
, Q
∗
, Ψ
∗
, Φ
∗
).
Очевидно, А
∗
= А и В
∗
= В. Положим Q
∗
= Q и Ψ
∗
= Ψ, а Φ
∗
определим
следующим образом. Пусть Ψ(a, q) = q
′
и Φ(q
′
) = b, где q, q
′
∈ Q, a ∈ А и b ∈ В.
Это означает, что автомат, будучи в состоянии q, отвечает на входной символ а
выходным символом b, который выдается в следующий момент времени, когда
автомат окажется в состоянии q
′
. Следовательно, можно считать, что
Φ
∗
(а, q) = b. Автомат Мура и эквивалентный ему автомат Мили представлены в
табл. 18.6 и 18.7 соответственно.
Пусть теперь задан автомат Мили М = (A, B, Q, Ψ, Φ) и требуется получить
эквивалентный ему автомат Мура М
∗
= (A
∗
, B
∗
, Q
∗
, Ψ
∗
, Φ
∗
). Как и в предыдущем
случае, имеем А
∗
= А и В
∗
= В. Определим Q
∗
следующим образом. Рассмотрим
все такие пары вида (q, b), где q ∈ Q, b ∈ B, что для каждой (q, b) имеется такая
пара (a, q
′
), что Ψ(a, q
′
) = q и Φ(a, q
′
) = b (a ∈ A, q
′
∈ Q). Каждой паре (q, b)
поставим в соответствие состояние q
∗
∈ Q
∗
и определим функции Ψ
∗
и Φ
∗
следующим образом:
Ψ
∗
(a, q
∗
) = Ψ
∗
(a, (q, b)) = (Ψ(a, q), Φ(a, q)); Φ
∗
(q
∗
) = Φ
∗
((q, b)) = b.
Таблица 18.6 Таблица 18.7
a
1
a
2
a
3
Φ
a
1
a
2
a
3
q
1
q
3
q
2
q
2
0 q
1
q
3
,0 q
2
,1 q
2
,1
q
2
q
1
q
4
q
3
1 q
2
q
1
,0 q
4
,1 q
3
,0
q
3
q
2
q
2
q
1
0 q
3
q
2
,1 q
2
,1 q
1
,0
q
4
q
3
q
4
q
4
1 q
4
q
3
,0
q
4
,1
q
4
,1
Если автомат имеет состояние, в которое он никогда не переходит (это
может быть начальное состояние), то всякому такому состоянию ставится в
