Поттосин Ю.В. Дискретная математика и теория проектирования цифровых устройств и систем
Подождите немного. Документ загружается.


141
соответствие состояние автомата Мура, переходы из него определяются
аналогично, а выходной символ при нем не определен.
Если автомат является частичным, то достаточно ввести новое состояние,
соответствующее неопределенному состоянию, и новый выходной символ,
соответствующий неопределенному выходному символу, и после описанных
преобразований вернуться к неопределенному состоянию и неопределенному
выходному символу. Переходы из такого состояния не определены. Автомат
Мили и эквивалентный ему автомат Мура представлены в табл. 18.8 и 18.9
соответственно.
Таблица 18.8 Таблица 18.9
a
1
a
2
a
3
a
4
a
1
a
2
a
3
a
4
Φ
∗
q
1
−,b
1
q
2
,b
1
−,−
q
2
,b
1
q
1
→
q
∗
1
q
∗
6
q
∗
2
−
q
∗
2
−
q
2
q
3
,b
1
−,b
2
q
3
,−
q
2
,b
1
q
2
,b
1
→
q
∗
2
q
∗
3
q
∗
7
q
∗
5
q
∗
2
b
1
q
3
q
3
,b
2
−,−
q
2
,b
1
q
2
,b
1
q
3
,b
1
→
q
∗
3
q
∗
4
−
q
∗
2
q
∗
2
b
1
q
3
,b
2
→
q
∗
4
q
∗
4
−
q
∗
2
q
∗
2
b
2
q
3
,−
→
q
∗
5
q
∗
4
−
q
∗
2
q
∗
2
−
−,b
1
→
q
∗
6
− − − −
b
1
−,b
2
→
q
∗
7
− − − −
b
2
18.4. Автомат с абстрактным состоянием. Булев автомат
Широко распространенным типом автомата является модель, описываемая
одной многозначной внутренней переменной q и многими входными и
выходными булевыми переменными х
1
, х
2
, … , х
п
и у
1
, у
2
, … , у
т
. Поведение
такого автомата задается системой уравнений
q
+
= ψ(х
1
, х
2
, … , х
п
; q);
y
1
= ϕ
1
(х
1
, х
2
, … , х
п
; q);
y
2
= ϕ
2
(х
1
, х
2
, … , х
п
; q);
…
y
m
= ϕ
m
(х
1
, х
2
, … , х
п
; q),
более компактно представляемой в векторной форме
q
+
= ψ(х, q);
y = ϕ(х, q).
Функции ψ и ϕ отличаются от введенных ранее Ψ и Φ только тем, что
многозначные входная и выходная переменные оказались замененными на
соответствующие булевы векторы, но внутренняя переменная осталась
многозначной.
142
Описанная модель называется автоматом с абстрактным состоянием.
Ею удобно пользоваться на начальных этапах логического проектирования
дискретных устройств, когда вход и выход устройства описываются как
некоторые множества булевых переменных, имеющих конкретную
техническую интерпретацию, в то время как множество внутренних
переменных представляется пока в простейшей форме, в виде одной
многозначной переменной q. Число значений переменной q полагается равным
числу различных состояний автомата, при котором он может реализовать
заданное функциональное отношение между входом и выходом.
Если заменить внутреннюю переменную q на соответствующий булев
вектор z = (z
1
, z
2
, … , z
k
), то получится система уравнений, в которой все
переменные и все функции оказываются булевыми:
z
1
+
= ψ
1
(х
1
, х
2
, … , х
п
; z
1
, z
2
, … , z
k
);
z
2
+
= ψ
2
(х
1
, х
2
, … , х
п
; z
1
, z
2
, … , z
k
);
…
z
k
+
= ψ
k
(х
1
, х
2
, … , х
п
; z
1
, z
2
, … , z
k
);
y
1
= ϕ
1
(х
1
, х
2
, … , х
п
; z
1
, z
2
, … , z
k
);
y
2
= ϕ
2
(х
1
, х
2
, … , х
п
; z
1
, z
2
, … , z
k
);
…
y
m
= ϕ
m
(х
1
, х
2
, … , х
п
; z
1
, z
2
, … , z
k
).
Эта модель называется булевым автоматом. Ее также можно представить
в компактной векторной форме:
z
+
= ψ(х, z);
y = ϕ(х, z).
Булев автомат в определенном смысле ближе к реальным дискретным
устройствам, поскольку его переменные непосредственно реализуются
физическими переменными устройства, в частности, на типичных для
современной техники элементах с двумя устойчивыми состояниями. Векторы х,
у и z показывают структуру абстрактных символов а и b и состояния q.
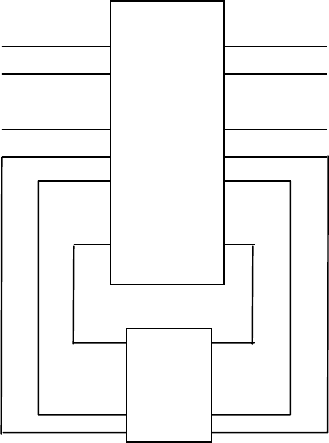
Приведенная выше система функций соответствует структуре, изображенной
на рис. 18.2, где КС – комбинационная схема, реализующая приведенную выше
систему, а П – блок памяти, осуществляющий задержку на период между
соседними моментами времени.
Переменная z
i
представляет состояние i-го двоичного элемента памяти, а
выражение
z
i
+
= ψ
i
(х
1
, х
2
, … , х
п
; z
1
, z
2
, … , z
k
)
143
надо понимать так, что состояние i-го элемента памяти определяется
значениями входных символов и состояниями элементов памяти в предыдущий
момент времени.
х
1
у
1
х
2
у
2
… …
х
п
у
т
z
1
z
1
+
z
2
z
2
+
… …
z
k
z
k
+
… …
Рис. 18.2. Структура булева автомата
KC
П
144
Г л а в а 19
Минимизация полных автоматов
19.1. Эквивалентность состояний. Постановка задачи минимизации
Одно и то же поведение может быть задано автоматами с различным
числом состояний. Отсюда возникает задача минимизации числа состояний
автомата, или просто минимизации автомата.
Основным понятием, используемым в данной задаче, является
эквивалентность состояний автомата. Состояние q
i
автомата М
1
и состояние q
j
автомата М
2
эквивалентны, если автомат М
1
при начальном состоянии q
i
и
автомат М
2
при начальном состоянии q
j
под воздействием любой входной
последовательности выдают одинаковые последовательности на выходе. При
этом М
1
и М
2
могут представлять собой один и тот же автомат.
Отношение эквивалентности состояний обладает свойствами
рефлексивности (каждое состояние эквивалентно самому себе),
симметричности (если состояние q
i
эквивалентно состоянию q
j
, то q
j
эквивалентно q
i
) и транзитивности (если состояние q
i
эквивалентно состоянию
q
k
, а q
k
эквивалентно состоянию q
j
, то q
i
эквивалентно q
j
). Как известно (см.
гл. 2), бинарное отношение на некотором множестве, обладающее такими
свойствами, определяет разбиение данного множества на классы
эквивалентности.
Автомат М
1
и автомат М
2
эквивалентны, если для каждого состояния
одного из них имеется хотя бы одно эквивалентное ему состояние другого.
Задача минимизации полного автомата ставится следующим образом: для
заданного автомата М найти эквивалентный ему автомат с минимальным
числом состояний.
Пусть задан автомат М = (A, B, Q, Ψ, Φ) и требуется найти эквивалентный
ему автомат М
′
= (A, B, Q
′
, Ψ
′
, Φ
′
), обладающий минимальным числом
состояний. Допустим, установлено отношение эквивалентности на множестве
состояний автомата М и определены классы эквивалентности S
1
, S
2
, … , S
т
.
Обозначим символом q
(
i
)
любое состояние, принадлежащее классу S
i
. Тогда
минимальный автомат строится следующим образом.
Формируется множество состояний Q
′
= {q
′
1
, q
′
2
, … , q
′
т
}, где каждому q
′
i
поставлен во взаимно однозначное соответствие класс эквивалентности S
i
.
Если для некоторых q
(
i
)
∈ S
i
и а ∈ А имеет место Φ(а, q
(
i
)
) = b, где b ∈ В, то
Φ
′
(а, q
′
i
) = b.
Если для некоторых q
(
i
)
∈ S
i
и а ∈ А имеет место Ψ(а, q
(
i
)
) = q
(
j
)
, где q
(
j
)
∈ S
j
,
то Ψ
′
(а, q
′
i
) = q
′
j
.
145
19.2. Установление эквивалентности состояний
В следующих трех случаях эквивалентность или неэквивалентность
состояний определяется непосредственно по таблицам переходов и выходов.
1. Найдется такой входной сигнал а ∈ А, что Φ(а, q
i
) ≠ Φ(а, q
j
). Тогда
состояния q
i
и q
j
явно неэквивалентны. В таблице выходов это соответствует
столбцу, где элементы в строках q
i
и q
j
различны.
2. Для всех а ∈ А имеют место Φ(а, q
i
) = Φ(а, q
j
) и Ψ(а, q
i
) = Ψ(а, q
j
). Здесь
состояния q
i
и q
j
явно эквивалентны. В таблице переходов и таблице выходов
строки q
i
и q
j
совпадают.
3. Строки q
i
и q
j
таблицы выходов совпадают, а строки q
i
и q
j
таблицы
переходов совпадут после замены каждого значения q
i
на q
j
или каждого
значения q
j
на q
i
(если, конечно, такие значения присутствуют в этих строках).
В этом случае состояния q
i
и q
j
также являются явно эквивалентными.
Если состояния не являются явно эквивалентными или явно
неэквивалентными, то для решения вопроса об их эквивалентности приходится
применять более глубокий анализ.
Пусть q
i
≠ q
j
. Цепью, порождаемой парой состояний 〈q
i
, q
j
〉 полного
автомата М, назовем множество С, элементами которого являются следующие
пары: 1) сама пара 〈q
i
, q
j
〉; 2) если 〈q
k
, q
l
〉 ∈ C, то все пары вида
〈Ψ(a, q
k
), Ψ(a, q
l
)〉, где Ψ(a, q
k
) и Ψ(a, q
l
) различны. Другие пары не входят в С.
Таким образом, цепь С, порождаемая парой состояний 〈q
i
, q
j
〉, содержит все
пары состояний, в которые автомат переходит из состояний q
i
и q
j
под
воздействием всевозможных входных последовательностей (конечных и
бесконечных). Само название «цепь» связано с характером образования этого
множества: реализуется процесс, подобный цепной реакции (появление одного
элемента в цепи вызывает вовлечение множества других элементов).
Справедливо следующее утверждение.
У т в е р ж д е н и е 19.1. Состояния q
i
и q
j
автомата М являются
эквивалентными, если и только если в цепи, порождаемой парой состояний
〈q
i
, q
j
〉, нет ни одной пары явно неэквивалентных состояний. В этом случае все
пары, принадлежащие данной цепи, являются парами эквивалентных
состояний.
Действительно, пусть состояние q
i
автомата М эквивалентно состоянию q
j
,
а цепь С, порождаемая парой 〈q
i
, q
j
〉, содержит пару явно неэквивалентных
состояний, скажем, 〈q
k
, q
l
〉. Тогда существует входная последовательность,
переводящая автомат М из состояний q
i
и q
j
в состояния q
k
и q
l
. Она вызывает
различные выходные последовательности, что противоречит условию. С другой
стороны, поскольку в С нет ни одной пары явно неэквивалентных состояний,
выходные последовательности при одной и той же входной последовательности
и при начальных состояниях q
i
и q
j
одинаковы.
146
Эквивалентность состояний можно представить матрицей
эквивалентности – булевой матрицей, строки и столбцы которой
соответствуют состояниям автомата. Элемент, расположенный на пересечении
i-й строки и j-го столбца, имеет значение 1, если и только если состояния q
i
и q
j
эквивалентны.
Рассмотрим процесс минимизации полного автомата на примере
(табл. 19.1).
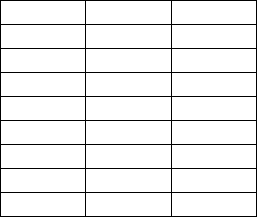
Таблица 19.1
Таблица переходов и выходов минимизируемого автомата
а
1
а
2
а
3
1 2,1 2,0 5,0
2 1,0 4,1 4,1
3 2,1 2,0 5,0
4 3,0 2,1 2,1
5 6,1 4,0 3,0
6 8,0 9,1 6,1
7 6,1 2,0 8,0
8 4,1 4,0 7,0
9 7,0 9,1 7,1
Сначала находим явно эквивалентные и явно неэквивалентные состояния.
В силу рефлексивности и симметричности отношения эквивалентности
достаточно иметь только часть матрицы эквивалентности, расположенную
выше (или ниже) главной диагонали. Получим следующую матрицу, пустые
элементы в верхней части которой соответствуют парам. Для этих пар
непосредственно из таблицы переходов и выходов не видно, эквивалентны в
них состояния или нет, т. е. не являются ни явно эквивалентными, ни явно
неэквивалентными:
8
7
6
5
4
3
2
1
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
10
98765432
.
Для пар состояний, которым соответствуют пустые места в этой матрице,
надо строить порождаемые ими цепи, которые удобно представлять
ориентированными графами. Вершинам такого графа соответствуют пары,
147
принадлежащие формируемой цепи. Из вершины 〈q
i
, q
j
〉 в вершину 〈q
k
, q
l
〉
направлена дуга, если 〈q
k
, q
l
〉 = 〈Ψ(a, q
i
), Ψ(a, q
j
)〉. Не обязательно строить всю
цепь, если порождающая ее пара не является эквивалентной. Можно прекратить
процесс после появления первой пары, которой соответствует нулевое значение
элемента матрицы эквивалентности. Тогда неэквивалентными объявляются все
пары, лежащие на пути к данной паре от порождающей пары.
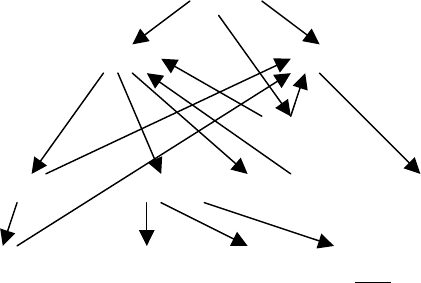
Часть цепи, порождаемой парой 〈1, 5〉, изображена на рис. 19.1. Она
содержит пару явно неэквивалентных состояний 〈2, 7〉. Дальше цепь можно не
строить, так как ясно, что пара 〈1, 5〉 оказалась неэквивалентной и, кроме нее,
неэквивалентными оказались пары 〈4, 9〉 и 〈2, 6〉, лежащие на пути из вершины
〈1, 5〉 к вершине 〈2, 7〉.
〈1, 5〉
〈2, 6〉 〈2, 4〉
〈3, 5〉
〈1, 8〉 〈4, 9〉 〈4, 6〉 〈1, 3〉
〈5, 7〉 〈3, 7〉 〈2, 9〉 〈2, 7〉
Рис. 19.1. Часть цепи, порождаемой парой 〈1, 5〉
Таким образом, матрица дополняется нулями в виде значений элементов,
соответствующих парам 〈1, 5〉, 〈2, 6〉 и 〈4, 9〉:
8
7
6
5
4
3
2
1
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
10
98765432
.
Состояния, принадлежащие паре 〈1, 7〉, также оказались
неэквивалентными. Цепь, порождаемая парой 〈1, 8〉 (рис. 19.2), не содержит пар

148
неэквивалентных состояний. Поэтому любая из пар, принадлежащих этому
множеству, является парой эквивалентных состояний. Окончательно получим
следующую матрицу эквивалентности:
8
7
6
5
4
3
2
1
0
0
0
0
0
0
0
0
0
0
0
0
1
0
1
0
1
0
0
0
0
0
0
0
0
0
0
0
0
0
0
1
0
0
10
98765432
.
〈1, 8〉
〈2, 4〉 〈5, 7〉
〈1, 3〉 〈3, 8〉
Рис. 19.2. Цепь,порождаемая парой 〈1, 8〉
Классы {1, 3, 8}, {2, 4}, {5, 7}, {6} и {9} определяются по строкам матрицы
эквивалентности с учетом свойства транзитивности и симметричности
отношения эквивалентности. Полученным классам эквивалентности ставим в
соответствие состояния нового автомата 1, 2, 3, 4 и 5, в результате чего
получим табл. 19.2, представляющую минимальный автомат, эквивалентный
заданному.
Таблица 19.2
Таблица переходов и выходов
минимального автомата
а
1
а
2
а
3
1 2,1 2,0 3,0
2 1,0 2,1 2,1
3 4,1 2,0 1,0
4 1,0 5,1 4,1
5 3,0 5,1 3,1
149
Г л а в а 20
Минимизация частичных автоматов
20.1. Отношение реализации. Постановка задачи минимизации
В случае полного автомата задача минимизации сводится к установлению
эквивалентности состояний и требуется найти автомат, поведение которого
совпадает с поведением исходного автомата. В случае частичного автомата
поведение искомого автомата с минимальным числом состояний должно
совпадать в тех ситуациях, где оно определено для исходного автомата. Здесь
понятие эквивалентности не подходит. Далее будет показано, что задача
минимизации частичного автомата не сводится к задаче минимизации полного
автомата. Для строгой формулировки задачи введем ряд понятий.
Пусть задан частичный автомат М = (A, B, Q, Ψ, Φ).
Входная последовательность
p
iii
aaa ...
21
называется допустимой для
состояния
1
i
q автомата М, если существует последовательность состояний
p
iii
qqq ...
21
, такая, что значение Φ ),(
pp
ii
qa и значения Ψ ),(
jj
ii
qa для 1 ≤ j ≤ p – 1
определены и Ψ
),(
jj
ii
qa
=
1+
j
i
q
.
При допустимой для некоторого состояния входной последовательности
автомат, выйдя из данного состояния, проходит вполне определенную
последовательность состояний. Выход автомата должен быть определен для
заключительного символа входной последовательности. Для промежуточных
символов это не обязательно. Если при какой-то входной последовательности
встретился неопределенный переход, то данная последовательность не является
допустимой для соответствующего начального состояния.
Состояние q
j
автомата М
2
реализует состояние q
i
автомата М
1
, если любая
входная последовательность, допустимая для q
i
, допустима и для q
j
, а
отвечающие ей выходные последовательности, полученные от автомата М
1
при
начальном состоянии q
i
и от автомата М
2
при начальном состоянии q
j
, совпадают
везде, где выходы автомата М
1
определены.
Отношение реализации, очевидно, является рефлексивным (любое
состояние реализует само себя) и транзитивным (из того, что q
i
реализует q
j
, а q
j
реализует q
k
, следует, что q
i
реализует q
k
). Это отношение не является
симметричным, т. е. из того, что q
i
реализует q
j
, не следует, что q
j
реализует q
i
.
Симметричность не обеспечивается из-за того, что реализующее состояние
может иметь более широкую область допустимых последовательностей, чем
реализуемое состояние.
Автомат М
2
реализует автомат М
1
, если для каждого состояния q
i
автомата
М
1
имеется по крайней мере одно состояние q
j
автомата М
2
, реализующее
150
состояние q
i
. Поведение автомата М
2
, реализующего автомат М
1
, совпадает с
поведением автомата М
1
везде, где поведение автомата М
1
определено.
Задача минимизации частичного автомата ставится следующим образом:
для заданного автомата М = (A, B, Q, Ψ, Φ) найти реализующий его автомат
М
′
= (A, B, Q
′
, Ψ
′
, Φ
′
) с минимальным числом состояний.
Сформулированная задача сводится к группированию состояний
исходного автомата в некоторые подмножества, в общем случае
пересекающиеся, и сопоставлению каждого такого подмножества с состоянием
нового автомата, реализующим любое состояние из этого подмножества. При
этом необходимо, чтобы число таких подмножеств было минимальным, а
объединение их составляло множество всех состояний исходного автомата.
Пусть имеется некоторая совокупность S подмножеств множества Q
состояний автомата М. Эти подмножества могут пересекаться, но ни одно из
них не содержится в другом. Совокупность S называется группировкой автомата
М, если каждое его состояние входит хотя бы в одно из подмножеств данной
совокупности.
Некоторое множество состояний {q
r
, q
s
, … , q
t
} ⊆ Q назовем
непосредственно производным по входному символу а ∈ А множеством от
множества состояний {q
i
, q
j
, … , q
k
} ⊆ Q, если значения
Ψ(а, q
j
), Ψ(а, q
j
), … , Ψ(а, q
k
) составляют множество {q
r
, q
s
, … , q
t
}.
Для множества состояний {q
r
, q
s
, … , q
t
} непосредственно производным от
него по входному символу а является множество тех состояний, в которые
автомат переходит из состояний q
r
, q
s
, … , q
t
при поступлении на его вход
символа а.
Множество состояний Q
i
⊆ Q называется непосредственно производным от
Q
j
⊆ Q, если найдется такой входной символ а ∈ А, что Q
i
является
непосредственно производным по а от Q
j
.
Группировка S называется правильной, если для каждого ее элемента S
i
справедливо следующее:
–
любое непосредственно производное от него множество является
подмножеством какого-то из элементов S;
–
для любых q
j
, q
k
∈ S
i
и для любого а ∈ А справедливо Φ(а, q
j
) = Φ(а, q
k
)
всегда, когда эти значения оба определены.
Для любого элемента S
i
правильной группировки автомата М и любого
входного символа а ∈ А можно найти в этой же группировке элемент,
содержащий все состояния, в которые переходит автомат М из состояний,
принадлежащих S
i
, при поступлении на его вход символа а.
Правильная группировка автомата М, имеющая минимальное число
элементов среди всех правильных группировок автомата М, называется
минимальной.
От любой правильной группировки автомата М можно перейти к автомату
М
′
, реализующему М, путем совмещения состояний, входящих в один и тот же
элемент группировки. Если {q
i
, q
j
, … , q
k
} – элемент правильной группировки S
