Пинчук С.И. Организация эксперимента при моделировании и оптимизации технических систем
Подождите немного. Документ загружается.


101
Статистической называют гипотезу о виде неизвестного рас-
пределения случайных величин или о параметрах известных рас-
пределений. Решение на основе выборочных наблюдений о том,
таков ли параметр генеральной совокупности или нет, называется
проверкой гипотезы. Если выдвинутая гипотеза неверна, мы её от-
брасываем.
Наряду с выдвинутой гипотезой, которую обычно называют нуле-
вой или основной и обозначают Н
0
, рассматривают и альтернатив-
ную гипотезу
Н
1
, противоречащую нулевой.
Вероятность того, что будет отброшена верная гипотеза
Н
0
, на-
зывают уровнем значимости и обычно обозначают
α. Величина α
выбирается равной 0,05 или 0,01 и связана с величиной надёжнос-
ти статистической оценки
γ следующим соотношением:
α = 1 – γ. (5.74)
Так,
α = 0,05, т.е. 5%-ный уровень значимости соответствует до-
верительной вероятности (надёжности) вывода γ = 0,95.
Ошибка, при которой гипотеза неверно отбрасывается, называ-
ется ошибкой первого рода. Принимая гипотезу, которая на самом
деле неверна, мы совершаем ошибку, которая называется ошибкой
второго рода, её вероятность обычно обозначается β.
Возвратимся к названному выше методу обнаружения промахов.
Вычисляют абсолютную величину максимального относительного
отклонения
τ = |x
i
– x|
max
/S (5.75)
и выдвигают гипотезу о том, что оно меньше критической величи-
ны
τ, определяемой по таблицам при выбранном уровне значимос-
ти
α и числе степеней свободы f = n – 2:
τ ≤ τ
табл.α;f
. (5.76)
Если это соотношение соблюдается, то проверяемый результат
измерения признаётся доброкачественным. В противном случае
гипотеза о доброкачественности проверяемого результата изме-
рения отбрасывается. Этот результат должен быть исключён из вы-
борки.
Сначала проверяют наибольший и/или наименьший по абсолют-
ной величине элементы выборки, по которой рассчитывались
x и S,
затем процедуру проверки можно повторить и для следующих по
величине результатов измерений и их отклонений.
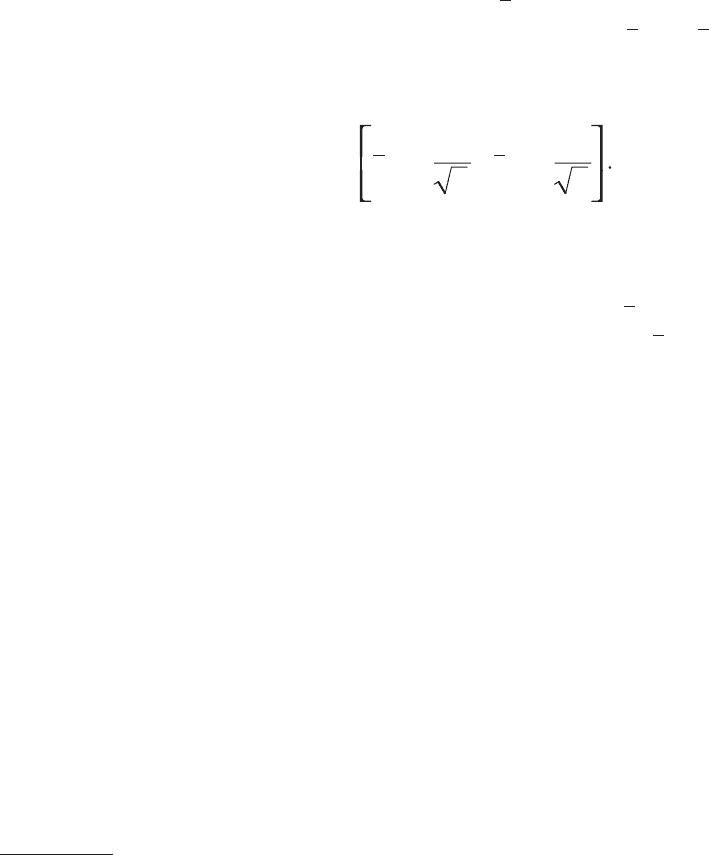
102
Допускается исключение одного или двух промахов из выбор-
ки. При этом целесообразно, по возможности, выполнить дополни-
тельные измерения для восстановления первоначального объёма
выборки. Если же обнаруживается более двух промахов, то вся вы-
борка признаётся недоброкачественной.
После исключения того или иного наблюдения характеристики
эмпирического распределения должны быть пересчитаны по доб-
рокачественным данным.
5.5.3
интервальная оценка истинного значения
измеряемого параметра
Истинное значение измеряемого параметра
Х можно оценить по
величине математического ожидания x при помощи доверительных
интервалов. Доверительным является интервал
[x
– δ, x
+ δ], где
для определения
δ используют выборочную оценку стандартного
отклонения S и t-критерий Стьюдента t
γ
:
x
– t
γ
S
,
n
x
+ t
γ
S
n
(5.77)
Значение
t
γ
определяют по таблице.
Напомним, что надёжностью или доверительной вероятностью
оценки измеряемой величины параметра
Х по x
называют веро-
ятность γ
, с которой осуществляется неравенство |x
– X| < δ. При
этом интервал значений х
і
, в который с заданной надёжностью по-
падает истинное значение измеряемого параметра Х, называется
доверительным интервалом. Доверительный интервал характери-
зует точность измерений в данной выборке, доверительная веро-
ятность – достоверность измерений.
5.5.4
сравнение интервальных оценок измеряемого параметра
Иногда необходимо проверить гипотезу о статистической зна-
чимости различия выборочных средних значений измеряемого
параметра в двух сериях измерений при различной величине до-
верительных интервалов. Целью эксперимента нередко бывает вы-
явление различий между оценками изучаемого параметра в разных
объектах исследования, а не только в разных сериях измерений.
Для выяснения вопроса о случайном или неслучайном расхож-
дении оценок параметра
Х по результатам двух серий измерений
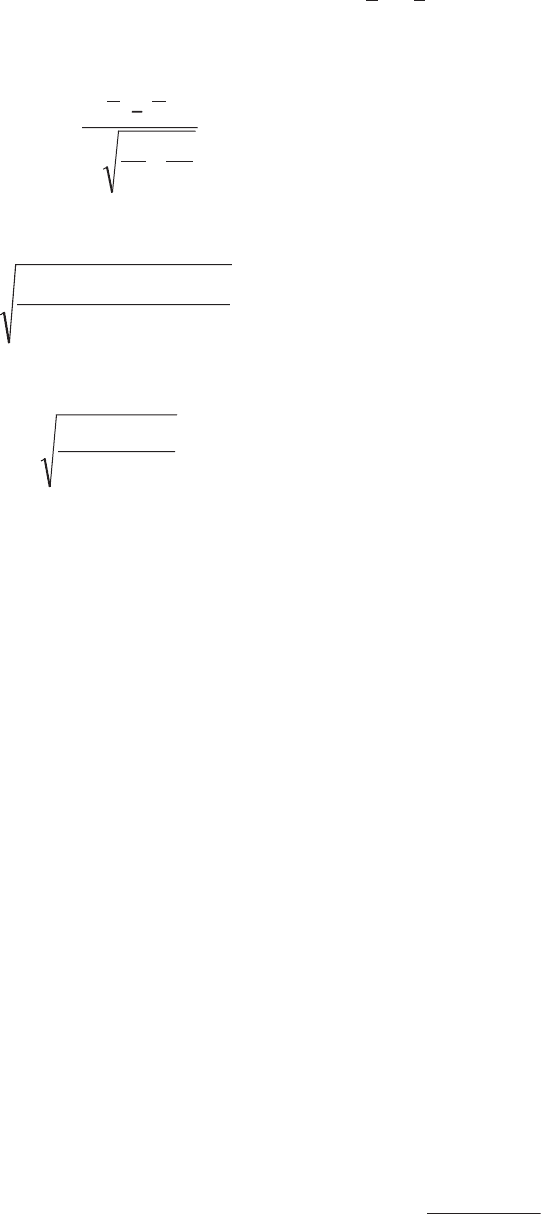
103
для каждой из них подсчитывают: средние арифметические x
1
и x
2
из
n
1
и n
2
числа измерений, дисперсии
S
1
2
и
S
2
2
, а затем рассчитыва-
ют значение
t
расч.
:
.
n
1
+
n
1
Q
хх
=t
21
21
расч.
(5.78)
Величина
Q может быть определена из выражения:
,
)1–)+(n1–(n
) S1–+ (n) S1–(n
Q
21
2
22
2
11
=
(5.79)
либо (при достаточно больших
n
1
и n
2
) из выражения:
.
2–+ nn
S+ nSn
Q =
21
2
22
2
11
(5.80)
Гипотеза о статистической значимости различия между оценка-
ми параметра Х по результатам двух серий измерений принимает-
ся, если выполняется соотношение:
|t
расч.
| ≥ t
табл. α; f = n
1
+ n
2
– 2
. (5.81)
5.5.5 проверка гипотезы о нормальности распределения
случайных ошибок измерений
При большом объёме выборки для основательной проверки ги-
потезы о нормальности распределения применяют правило трёх
сигм либо
χ
2
– критерий.
Для выборок небольшого объёма (n ≤ 20÷30) могут быть
использованы приближённые методы проверки гипотезы о нор-
мальности распределения случайных ошибок измерений.
Метод, основанный на сравнении выборочных исправленных
среднего абсолютного и квадратичного отклонений
m и S
Если m ≈ 0,8S или, соответственно, S ≈ 1,25m, то гипотеза о нор-
мальности распределения может быть принята.
Для выборки, имеющей приблизительно нормальное распреде-
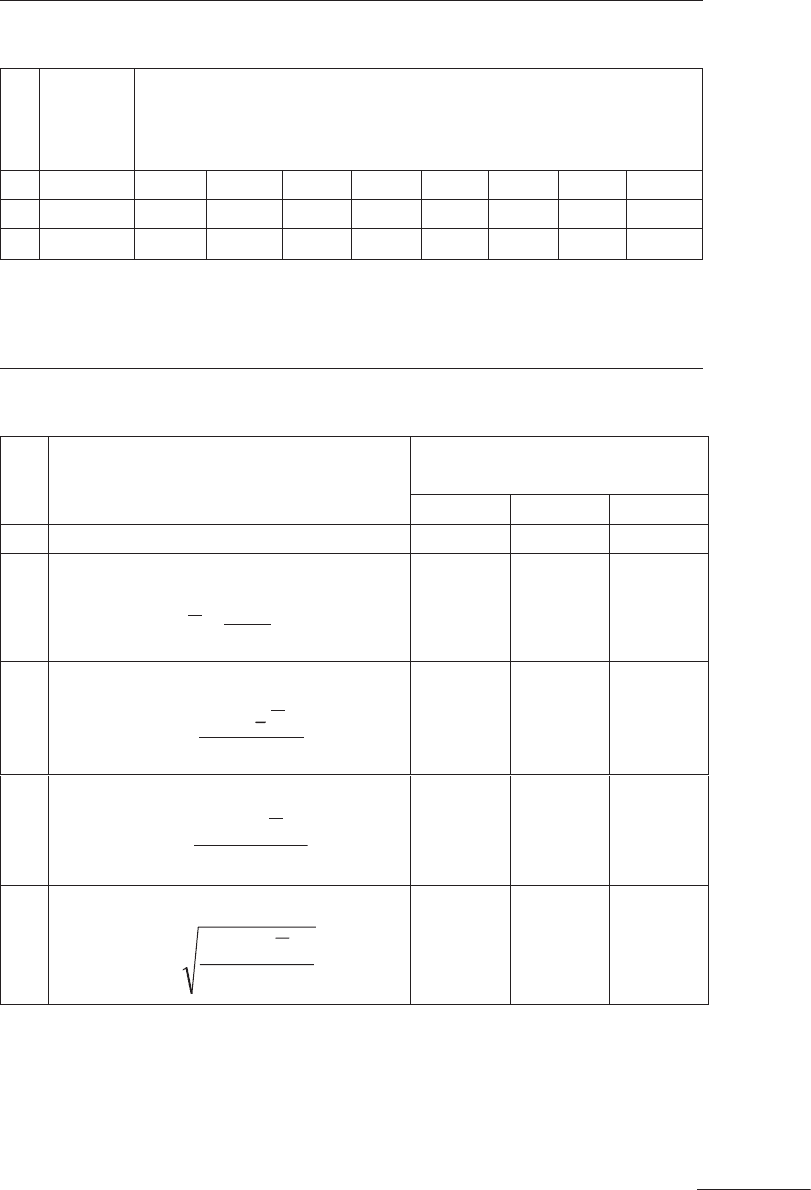
ление, должно быть справедливым также соотношение:

104
|f/S – 0,7979| < 0,4/
√n
, (5.82)
где величина среднего абсолютного отклонения
f определяется по
формуле (5.44).
Метод, основанный на использовании размаха варьирования
R
Сравнивают отношение R/S c критическими (при выбранном
уровне значимости
α) верхней и нижней границами этого отноше-
ния, приведёнными в таблице. Если
R/S меньше нижней или боль-
ше верхней критической границы, гипотеза о нормальности рас-
пределения не принимается.
Метод, основанный на использовании коэффициентов
асимметрии и эксцесса
Если коэффициенты асимметрии и эксцесса не равны
0 и выпол-
няются условия:
|A| ≤ 2S
A
или |A
1
| ≤ 3S
A
1
; (5.83)
|E| ≤ 3S
E
или |E
1
| ≤ 5S
E
1
, (5.84)
то гипотеза о нормальности распределения случайных ошибок из-
мерений может быть принята.
5.6 пример первичной обработки
экспериментальных данных
Рассмотрим приёмы первичной обработки данных однофак-
торного эксперимента при изучении зависимости плотности прес-
совок металлического порошка никеля от давления прессования*.
Из трёх партий прессовок порошка никеля, полученных при давлени-
ях прессования (МПа) Р
1
= 220; Р
2
= 370 и Р
3
= 480, случайным обра-
зом отобрали по 8 прессовок и измерили их плотность ρ (г/см
3
).
Результаты измерений приведены в табл. 5.3.
*Примечание. Изделия из металлических порошков получают метода-
ми порошковой металлургии. Технология предусматривает загрузку подго-
товленных порошков или их смесей в пресс-формы для получения «формо-
вок», их прессование при определённых давлениях для придания требуемой
плотности и других характеристик и последующее спекание полученных
таким образом «прессовок».
105
Таблица 5.3
Результаты измерений плотности прессовок
Выборка
Давле-
ние
Р, МПа
Плотность ρ, г/см
3
1 220 5,414 5,245 5,278 5,240 5,129 5,662 5,598 5,509
2 370 6,264 5,644 6,171 5,993 5,995 5,530 6,201 5,232
3 480 6,349 6,142 6,133 6,001 5,862 6,094 6,063 5,778
В табл. 5.4 приведены численные характеристики выборок.
Таблица 5.4
Численные характеристики выборок
№
Наименование и формулы
для вычисления
Численные значения
характеристик выборок
1 2 3
1 2 3 4 5
1
Математическое ожидание
n
ρ
=
ρ
i
∑
5,3844 5,8788 6,0528
2
Дисперсия
n
)
ρ
(
ρ
=σ
2
i
2
∑
0,0320 0,1199 0,0273
3
Несмещённая дисперсия
1–n
)
ρ–(ρ
=S
2
i
2
∑
0,03656 0,1370 0,0312
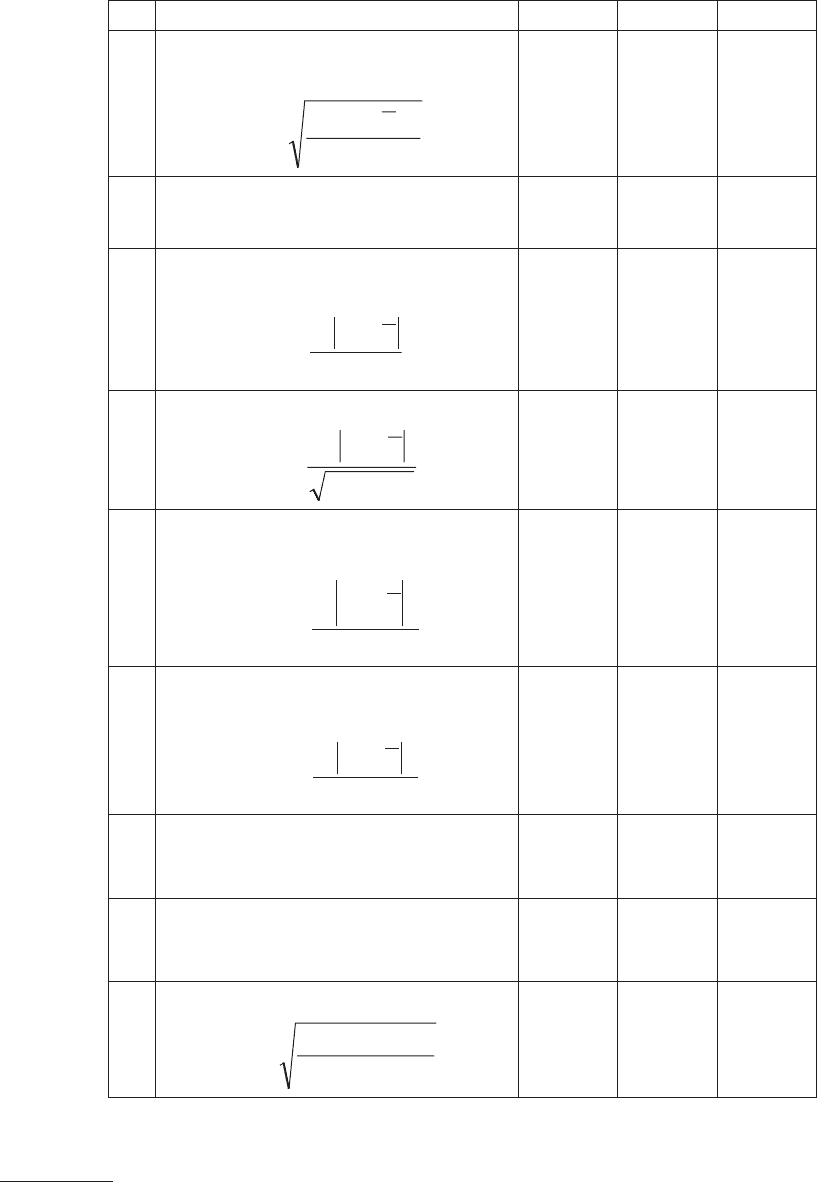
4
Стандартное отклонение
n
)ρ–(ρ
σ =
2
i
∑
0,1789 0,3463 0,1653
106
1 2 3 4 5
5
Исправленное стандартное
отклонение
1–n
)ρ–(ρ
S =
2
i
∑
0,1912 0,3702 0,1767
6
Размах варьирования
R = ρ
max
– ρ
min
0,5330 1,0320 0,5710
7
Среднеарифметическое
отклонение (САО)
f =
n
ρ–ρ
i
∑
0,1614 0,3076 0,1293
8
Исправленное САО
)1–n(n
ρ–ρ
m =
i
∑
0,1725 0,3288 0,1382
9
Центральный
момент М
3
=M
3
n
ρ–
i
ρ
3
∑
0,00709 0,05557 0,00689
10
Центральный
момент М
4
=M
4
n
ρ–ρ
4
i
∑
0,00168 0,0292 0,0019
11
Коэффициент асимметрии А
2/3
23
/MА = M
1,2383 1,3383 1,5261
12
Эксцесс Е
3–/ME = M
2
2
4
–1,3561 –0,9721 –0,5140
13
Стандартное отклонение А
)3)(n +1(n +
)1–n(n 6
=S
A
1,8423 1,8423 1,8423
Продолжение табл. 5.4.
107
1 2 3 4 5
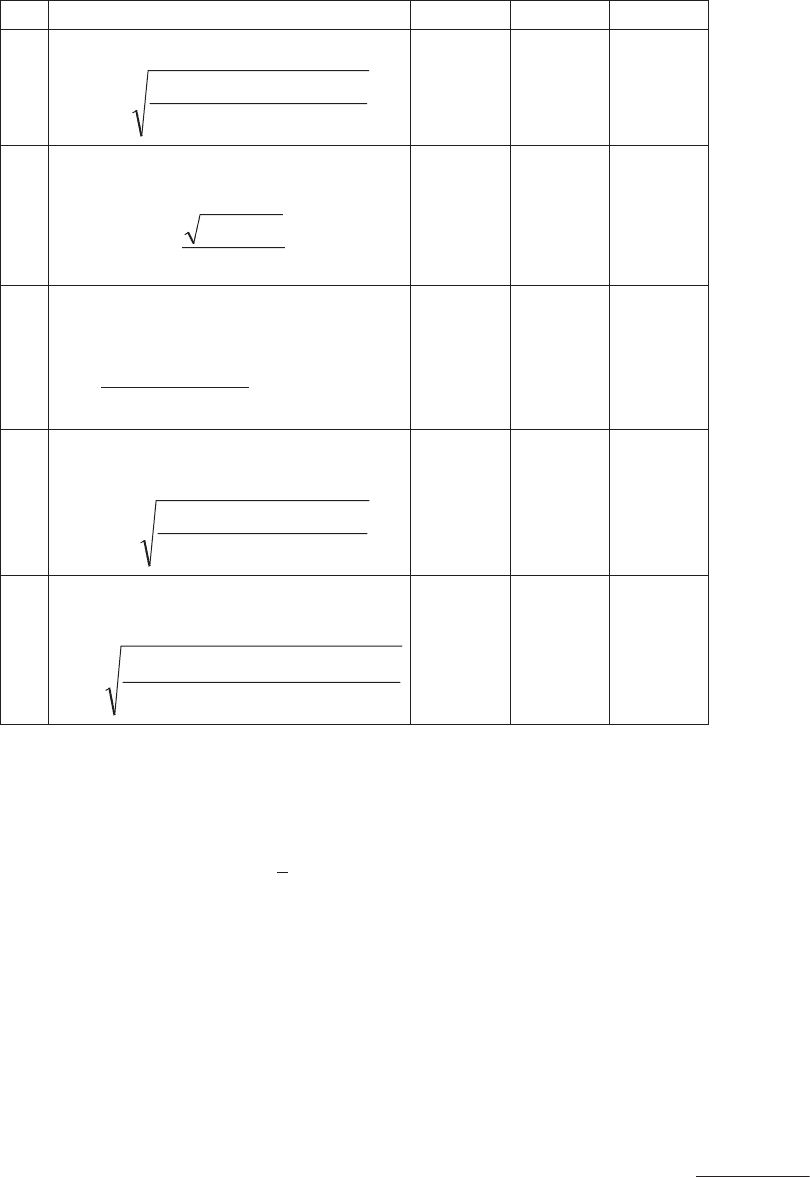
14 Стандартное отклонение Е
)5)(n +3(n +)1–(n
)3–)(n2–n(n24
=S
2
E
0,9067 0,9067 0,9067
15
Несмещённая оценка выбороч-
ного коэффициента асимметрии
· A
2–n
)1–n(n
=
A
1
1,5445 1,6692 1,9034
16
Несмещённая оценка
выборочного эксцесса
[]
6) E +1(n +
)3–)(n2–(n
1–n
=E
1
–1,4479 –0,6414 0,3207
17
Исправленная оценка стандарт-
ного отклонения A
1
)3)(n1)(n2–(n
)1–n(n6
=S
1
A
++
0,7521 0,7521 0,7521
18
Исправленная оценка стандарт-
ного отклонения E
1
)5)(n3)(n2–)(n3–(n
)1–n(n24
=S
2
E
1
++
1,4809 1,4809 1,4809
5.6.1 проверка наличия промахов в выборках
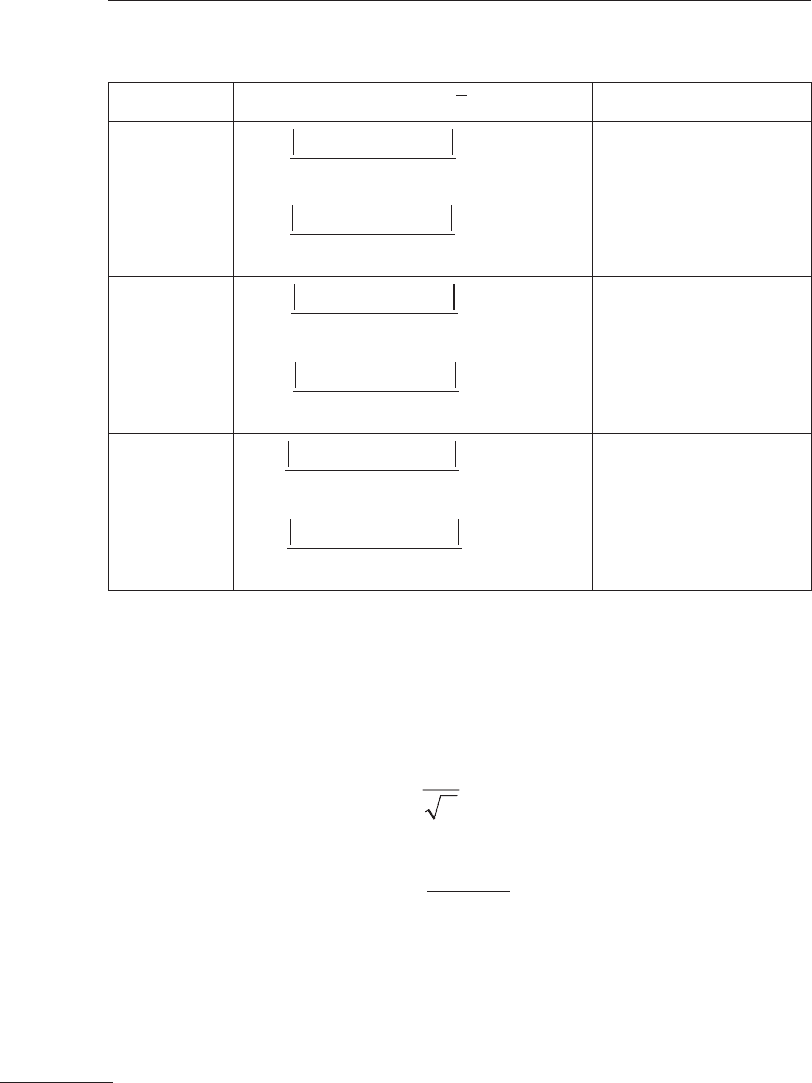
Проверку гипотезы о наличии грубых ошибок (промахов) при оп-
ределении плотности прессовок выполняем путём сопоставления
величин отношений
|ρ
i
– ρ
|/S в выборках с табличным значением
максимального (критического) относительного отклонения
τ
α, f = n–2
.
Для проверки наличия промахов используем первую и пятую по-
зиции табл. 5.4.
Продолжение табл. 5.4.
108
При объёме выборок n = 8 и f = 6 табличная величина τ
α, f
со-
ставляет
2,172. Сопоставление рассматриваемых параметров пред-
ставлено в табл. 5.5.
Таблица 5.5
Данные для проверки гипотезы о наличии промахов
при определении плотности прессовок
Выборка
Расчёт
|ρ
i
– ρ
|/S
Вывод
1
336,1=
1912,0
3844,5–129,5
452,1=
1912,0
3844,5–662,5
Выборка промахов
не имеет
2
747,1=
3702,0
8788,5–232,5
041,1=
3702,0
8788,5–264,6
Выборка промахов
не имеет
3
555,1=
1767,0
0528,6–778,5
676,1=
1767,0
0528,6–349,6
Выборка промахов
не имеет
Итак, промахов в выборках не обнаружено, все значения
ρ
i
, при-
веденные в табл. 5.3., доброкачественны и пересчёту не подлежат.
5.6.2 Определение интервальных оценок
плотности прессовок
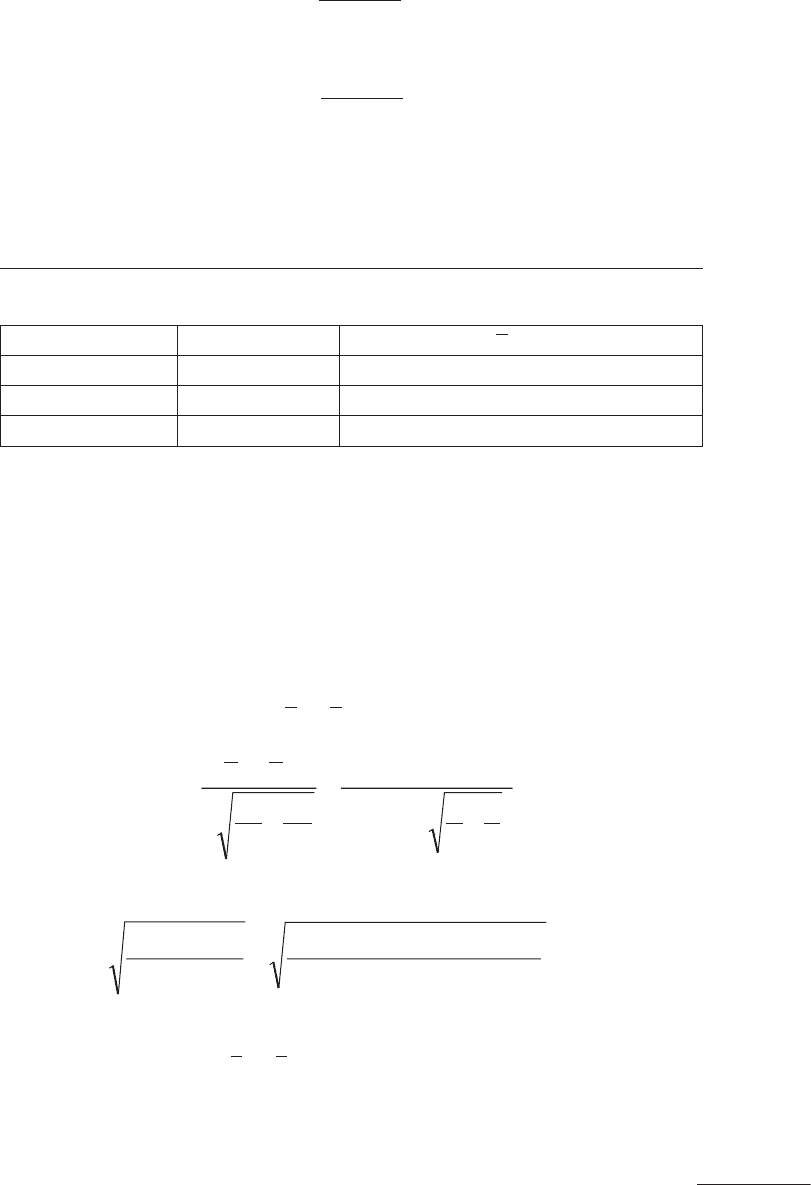
Вычисляем значения
n
S
δ = t
γ
. При α = 0,05 и n = 8 табличное
значение t
y
= 2,31.
1562;,0=
8284,2
1912,0
31,2=δ
1
109
3023;,0=
8284,2
3702,0
31,2=δ
2
.1443,0=
8284,2
1767,0
31,2=δ
3
В таблице 5.6 приведены интервальные оценки плотности прес-
совок из порошка никеля при давлениях прессования
Р
1
, Р
2
и Р
3
.
Таблица 5.6
Интервальные оценки плотности прессовок
Выборка
δ ρ
± δ
1 0,1562 0,1912 ± 0,1562
2 0,3023 0,3702 ± 0,3023
3 0,1443 0,1767 ± 0,1443
5.6.3 проверка гипотезы о статистической значимости
различия плотности прессовок, полученных
при различных давлениях прессования
Если
|t
расч.
| ≥ t
табл. α; f
, то различия сравниваемых плотностей
прессовок статистически значимы.
При
α = 0,05 и n
1
= n
2
= n
3
= 8 f = 14 и t
табл.
= 2,15.
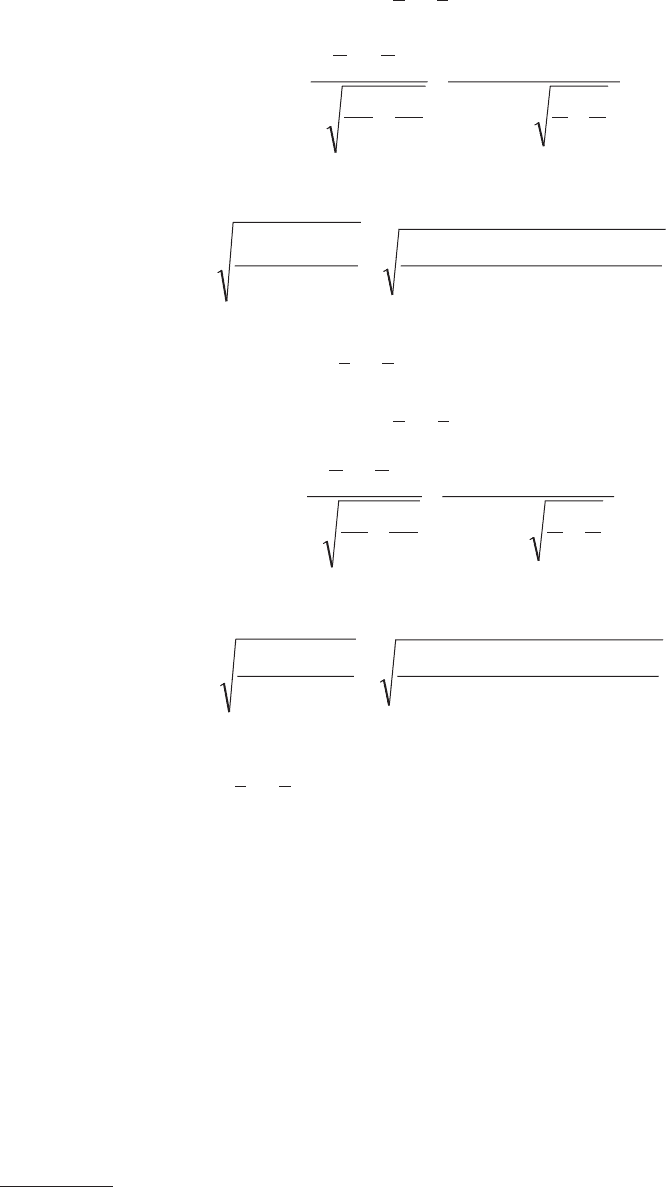
Проверяем гипотезу о статистической значимости различия меж-
ду значениями плотностей
ρ
1
и ρ
2
.
,139,3=
8
1
+
8
1
3149 ·,0
8788,5–3844,5
=
n
1
+
n
1
S
ρ–ρ
=t
21
21
расч.
где
.3149,0=
2–8+8
3702,08 ·+1912,08 ·
=
2–+ nn
S+nSn
S=
22
21
2
22
2
11
Так как 3,139 > 2,15, то гипотеза о статистической значимости
различия плотностей ρ
1
и ρ
2
принимается.
110
Проверяем гипотезу о статистической значимости различия меж-
ду значениями плотностей
ρ
2
и ρ
3
.
,122,1=
8
1
+
8
1
3101 ·,0
0528,6–8788,5
=
n
1
+
n
1
S
ρ–ρ
=t
32
32
расч.
где
.3101,0=
2–88
1767,08 ·+3702,08 ·
=
2–nn
S+ nSn
S =
22
32
2
33
2
2
2
++
Так как 1,122 < 2,15, то гипотеза о статистической значимости
различия плотностей
ρ
2
и ρ
3
не принимается.
Проверяем гипотезу о статистической значимости различия меж-
ду значениями плотностей ρ
1
и ρ
3
.
,793,6=
8
1
+
8
1
1968 ·,0
0528,6–3844,5
=
n
1
+
n
1
S
ρ–ρ
=t
31
31
расч.
где
.1968,0=
2–8+8
1767,08 ·+1912,08 ·
=
2–+ nn
S+nSn
S =
22
31
2
33
2
11
Так как 6,793 > 2,15, то гипотеза о статистической значимости
плотностей
ρ
1
и ρ
3
принимается.
