Пинчук С.И. Организация эксперимента при моделировании и оптимизации технических систем
Подождите немного. Документ загружается.


91
Легко «исправить» выборочную дисперсию так, чтобы ее мате-
матическое ожидание было равно генеральной дисперсии. Доста-
точно для этого умножить
D
в
на дробь
1n
n
−
.
Сделав это, получим «исправленную дисперсию», которую обыч-
но обозначают через
S
2
:
1n
)x(xn
n
)x(xn
1n
n
D
1n
n
S
2
в
ii
2
в
ii
в
2
−
∑
−
=
∑
−
·
−
=
−
=
.
(5.37)
Исправленная дисперсия является несмещённой оценкой гене-
ральной дисперсии.
Для оценки среднего квадратичного отклонения генеральной сово-
купности используют «исправленное» среднее квадратичное отклоне-
ние, которое равно квадратному корню из исправленной дисперсии:
1n –
)x–(xn
S =
2
в
ii
∑
. (5.38)
S не является несмещенной оценкой; чтобы отразить этот факт, далее
будем писать так: «исправленное среднее квадратичное отклонение».
5.4.6 точность оценки, доверительная вероятность (надёжность).
доверительный интервал
Точечной называют оценку, которая определяется одним числом.
Все оценки, рассмотренные выше, – точечные. При выборке малого
объёма точечная оценка может значительно отличаться от оцени-
ваемого параметра, т.е. приводить к грубым ошибкам. По этой при-
чине при небольшом объеме выборки следует пользоваться ин-
тервальными оценками.
Интервальной называют оценку, которая определяется двумя
числами – концами интервала. Интервальные оценки позволяют ус-
тановить точность и надежность оценок.
Пусть найденная по данным выборки статистическая характерис-
тика
Θ* служит оценкой неизвестного параметра Θ. Будем считать
Θ постоянным числом (Θ может быть случайной величиной). Ясно, что
Θ* тем точнее определяет параметр Θ, чем меньше абсолютная вели-
чина разности |Θ – Θ*|. Другими словами, если δ > 0 и |Θ – Θ*| < δ то,
чем меньше δ, тем оценка точнее. Таким образом, положительное
число δ характеризует точность оценки.
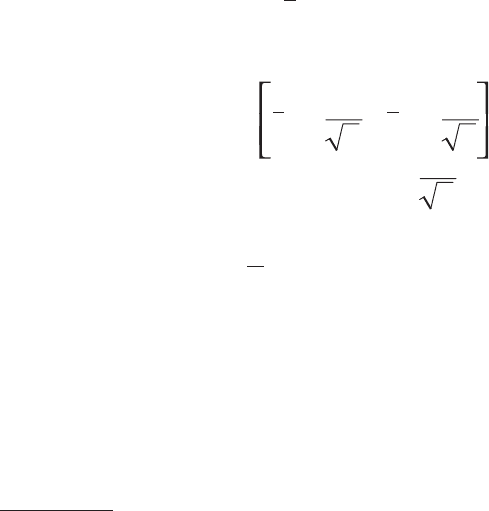
92
Однако, статистические методы не позволяют категорически ут-
верждать, что оценка
Θ* удовлетворяет неравенству |Θ – Θ*| < δ,
можно лишь говорить о вероятности
γ, с которой это неравенство
осуществляется.
Надежностью (доверительной вероятностью) оценки Θ по Θ*
называют вероятность
γ, с которой осуществляется неравенство
|Θ – Θ*| < δ. Обычно надежность оценки задается наперед, причем
в качестве
γ берут число, близкое к единице. Наиболее часто задают
надежность, равную
0,95; 0,99 и 0,999.
Пусть вероятность того, что |Θ – Θ*| < δ равна γ:
P[|Θ – Θ*| < δ] = γ.
Заменим неравенство |Θ – Θ*| < δ равнозначным ему двойным
неравенством
– δ < (Θ – Θ*) < δ или (Θ* – δ) < Θ < (Θ* + δ). (5.39)
Тогда
P[(Θ* – δ) < Θ < (Θ* + δ)] = γ. (5.40)
Это соотношение следует понимать так: вероятность того, что
интервал
[Θ* – δ, Θ* + δ] заключает в себе (покрывает) неизвест-
ный параметр Θ, равна γ.
Доверительным называют интервал [Θ* – δ, Θ* + δ], который
покрывает неизвестный параметр с заданной надежностью γ.
Если случайная величина X распределена нормально, то выбо-
рочная средняя
x
в
, найденная по независимым наблюдениям, так-
же распределена нормально. При известном среднеквадратичном
отклонении σ с надежностью γ можно утверждать, что доверитель-
ный интервал
x
в
– t
σ
;
n
x
в
+ t
σ
n
покрывает неизвестный пара-
метр Х; точность оценки
δ
= t
σ
n
. Число t определяется по таблице
(находят аргумент
t, ему соответствует значение функции Лапласа
Ф(t), равное
2
γ
).
При возрастании объема выборки n число δ убывает и, следо-
вательно, точность оценки увеличивается. Увеличение надежности
оценки γ приводит к увеличению t, a следовательно, и к возраста-
нию δ. Другими словами, увеличение надежности оценки влечет за
собой уменьшение ее точности.

93
При неизвестном среднеквадратичном отклонении σ можно найти
доверительный интервал, покрывающий неизвестный параметр
Х с
надежностью
γ, пользуясь распределением Стьюдента и величиной S.
x
в
– t
γ
S
;
n
x
в
+ t
γ
S
n
(5.41)
Здесь использованы величины
x
в
и S, найденные по выборке, а
по заданным
n и γ можно найти значения t
γ
(t - критерия Стьюден-
та) по таблице.
Распределение Стьюдента определяется параметром n – объе-
мом выборки (или числом степеней свободы*) и не зависит от неиз-
вестных параметров
Х и σ. Эта особенность является большим до-
стоинством распределения Стьюдента.
При неограниченном возрастании объема выборки
n распре-
деление Стьюдента стремится к нормальному. Поэтому при
n > 30
можно вместо распределения Стьюдента пользоваться нормаль-
ным распределением.
Однако, важно подчеркнуть, что для малых выборок
(n < 20÷30),
в особенно для малых значений n, замена распределения нормаль-
ным может приводить к грубым ошибкам, а именно: к неоправдан-
ному сужению доверительного интервала, т.е. к неоправданному
повышению точности оценки.
Итак, истинное значение измеряемого параметра можно оцени-
вать по среднему арифметическому результатов отдельных измере-
ний при помощи доверительных интервалов.
5.4.7
другие характеристики вариационного ряда
Кроме выборочной средней и выборочной дисперсии применя-
ются и другие характеристики вариационного ряда.
Модой М
0
называют варианту, которая имеет наибольшую часто-
ту. Например, для ряда
х
i
1 4 7 9
n
i
5 1 20 6
мода равна 7.
*Числом степеней свободы называется число наблюдений минус число
оцененных по ним параметров.

94
Медианой m
е
называют варианту, которая делит вариационный
ряд на две части, равные по числу вариант. Если число вариант не-
четно, т.е.
n = 2k + 1, то m
e
= х
(k + 1)
; при четном n = 2k медиана
2
+ xx
=m
)1(k+k
e
(5.42)
Например, для ряда вариант
2 3 5 6 7 медиана равна 5; для ряда
вариант
2 3 5 6 7 9 медиана равна
5,5=
2
5 + 6
.
Размахом варьирования
R называют разность между наибольшей
и наименьшей вариантами:
R = x
max
– x
min
. (5.43)
Например, для ряда варианта
1 3 4 5 6 10
размах
R равен 10 – 1 = 9.
Размах является простейшей характеристикой рассеяния вариа-
ционного ряда.
Средним абсолютным отклонением
f называют среднее арифме-
тическое абсолютных отклонений:
∑
∑
i
в
ii
n
xxn
f =
. (5.44)
Например, для ряда
х
i
1 3 6 16
n
i
4 10 5 1
имеем:
;4=
20
80
=
4 + 10 + 5 + 1
4 · 1 + 10 · 3 + 5 · 6 + 1 · 16
=
x
в
= 2,2.
20
4 ·
|1 – 4| + 10 · |3 – 4| + 5 · |6 – 4| + 1 · |16 – 4|
f =
Среднее абсолютное отклонение служит для характеристики
рассеяния вариационного ряда.
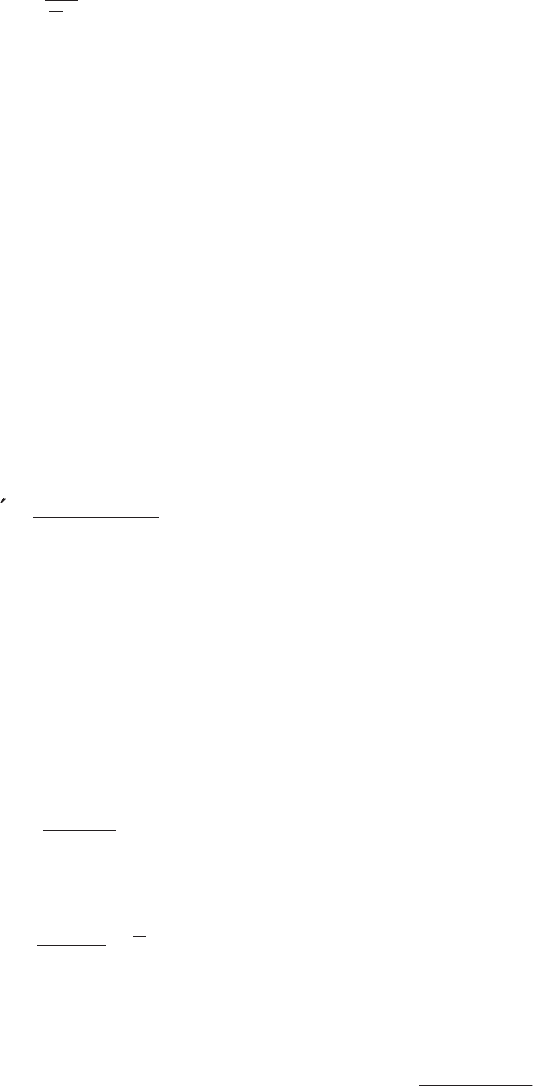
95
Коэффициентом вариации υ называют выраженное в процентах
отношение выборочного среднего квадратичного отклонения к вы-
борочной средней:
, %100
x
σ
υ =
в
в
. (5.45)
Коэффициент вариации служит для сравнения величин рассея-
ния двух вариационных рядов: тот из рядов имеет большее рассея-
ние, у которого коэффициент вариации больше.
Выше предполагалось, что вариационный ряд составлен по дан-
ным выборки, поэтому все описанные характеристики называют вы-
борочными. Если вариационный ряд составлен по данным генераль-
ной совокупности, то характеристики называют генеральными.
Для вычисления сводных характеристик выборки удобно поль-
зоваться эмпирическими моментами, определения которых анало-
гичны определениям соответствующих теоретических моментов.
В отличие от тео ретических эмпирические моменты вычисляют по
данным наблюдений.
Обычным эмпирическим моментом порядка k называют среднее
значение
k-x степеней разностей (x
i
– c):
n
c)(xn
=M
k
–
ii
k
∑
,
(5.46)
где
х
i
– наблюдаемая варианта,
n
i
– частота варианты,
п = ∑п
i
– объем выборки,
с – произвольное постоянное число (ложный нуль).
Начальным эмпирическим моментом порядка
k называют обыч-
ный момент порядка k при с = 0.
n
xn
=m
k
ii
k
∑
. (5.47)
В частности,
в
ii
1
x=
n
xn
=m
∑
, (5.48)
т. е. начальный эмпирический момент первого порядка равен вы-
борочной средней.

96
Центральным эмпирическим моментом порядка k называют
обычный момент порядка
k при c =
x
в
.
k
в
ii
k
n
)x–(x∑n
=M
. (5.49)
В частности,
в
2
в
ii
2
= D
n
)x–(xn
=M
∑
, (5.50)
т. е. центральный эмпирический момент второго порядка равен вы-
борочной дисперсии.
Легко выразить центральные моменты через обычные:
M
2
= Mʹ
2
– (Mʹ
1
)
2
; (5.51)
M
3
= Mʹ
3
– 3Mʹ
2
Mʹ
1
+ 2(Mʹ
1
)
3
; (5.52)
M
4
= Mʹ
4
– 4Mʹ
3
Mʹ
1
+ 6Mʹ
2
(Mʹ
1
)
2
– 3(Mʹ
1
)
4
. (5.53)
В случае непрерывного распределения вероятности отдельных
возможных значений равны нулю. Поэтому весь интервал возмож-
ных значений делят на
k непересекающихся интервалов и вычисля-
ют вероятности Р попадания значений X в i-й частичный интервал,
а затем, как и для дискретного распределения, умножают число ис-
пытаний на эти вероятности.
Для оценки отклонения эмпирического распределения от нор-
мального используют различные характеристики, к числу которых
относятся асимметрия и эксцесс. Определения этих характеристик
аналогичны определениям асимметрии и эксцесса теоретического
распределения.
Асимметрия эмпирического распределения определяется ра-
венством
,
М
М
или А =
σ
М
А =
2/3
2
3
3
в
3
(5.54)
где
М
2
и M
3
– центральные эмпирические моменты второго и тре-
тьего порядка,
σ
в
– выборочное среднеквадратичное отклонение, т.е.
√M
2
.

97
Эксцесс эмпирического распределения определяется равенством
,3–
М
М
или
Е =3–
σ
М
Е =
2
2
4
4
в
4
(5.55)
где M
4
– центральный эмпирический момент четвертого порядка.
5.5 приёмы первичной обработки экспериментальных
данных
5.5.1 систематизация данных измерений и нахождение
числовых характеристик измеряемых величин
Важнейшими задачами обработки экспериментальных данных
являются отсеивание результатов измерений с грубыми погреш-
ностями и проверка соответствия распределения результатов из-
мерений законам нормального распределения.
Систематизация экспериментальных данных предполагает их
размещение в таблицах. Материал располагают в хронологической
последовательности (получают временные ряды случайных вели-
чин) либо в соответствии с изменением изучаемых параметров (по-
лучают статистические ряды распределения).
В математической статистике распределение рассматривают как
соответствие между наблюдаемыми значениями параметра и их
частотами – абсолютными либо относительными (см. в разделе 5.4).
Определяют диапазон изменения измеряемых величин, т.е. диапа-
зон варьирования результатов измерений. Количественной оценкой
этого диапазона является размах вариации
R, величина которого оп-
ределяется как разность между полученными максимальным и мини-
мальным значениями измеряемого параметра Х по формуле (5.43):
R = х
max
– х
min
.
Для проверки наличия грубых ошибок измерений параметра
Х
необходимо по данным ряда наблюдений получить статистическую
оценку величины измеряемого параметра и статистические оцен-
ки колеблемости результатов измерений.
Математическое ожидание измеряемого параметра
Х находят
как среднее арифметическое результатов наблюдений по форму-
лам (5.31) либо (5.32).
Для оценки колеблемости результатов измерений переменных
или отклонений результатов их измерений
х
і
от средней величи-
98
ны x используют среднее абсолютное отклонение, дисперсию и
среднее квадратичное (стандартное) отклонение.
Заметим, что характеристики распределения в генеральной со-
вокупности называют параметрами. Их принято обозначать буквами
греческого алфавита, например, дисперсия
σ
2
, среднее квадратич-
ное отклонение
σ. Выборочные характеристики называют оценка-
ми или статистиками. Их принято обозначать буквами латинского
алфавита, например, дисперсия
S
2
и среднее квадратичное откло-
нение
S.
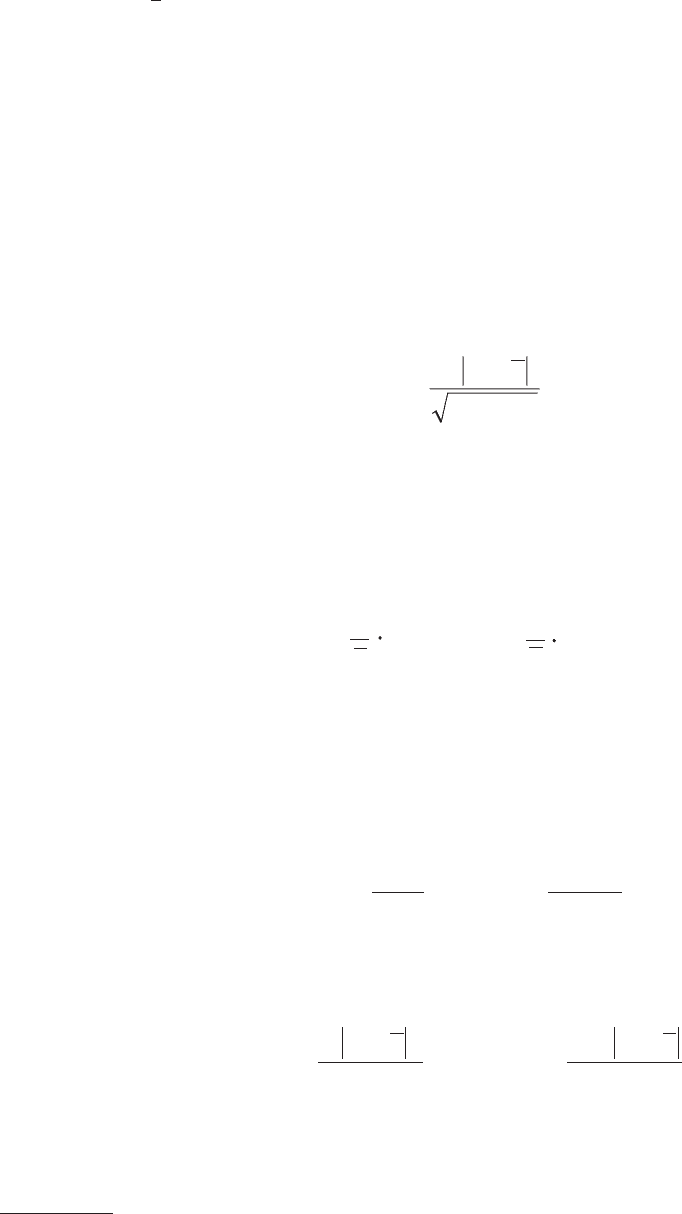
Определяют следующие оценки колеблемости выборочных дан-
ных:
исправленное среднее абсолютное отклонение:
)1n(n
x–
–
x
m =
i
∑
; (5.56)
исправленную дисперсию
S
2
по формуле (5.37) и исправленное сред-
неквадратичное (стандартное) отклонение S по формуле (5.38).
Для сравнения колеблемости переменных, имеющих разные раз-
мерности, удобно применять коэффициенты вариации: для гене-
ральной совокупности – υ
σ
и для выборки – υ
s
:
,%;100
x
σ
=υ
σ
,%.100
x
S
=υ
s
(5.57)
Среднее арифметическое является начальным моментом перво-
го (
m
1
), дисперсия – центральным моментом второго (M
2
) порядка
выборки случайных величин х
і
. Напомним, что начальным момен-
том порядка k случайной величины называется её математическое
ожидание
k-ой степени:
n
x
=m
k
i
k
∑
или
n
xn
=m
k
ii
k
∑
;
центральным моментом порядка k называется математическое ожи-
дание k-ой степени отклонения величины Х от её центра:
=
n
x–x
k
i
∑
или
k
ii
k
n
x–xn
=M
k
M
∑
.
Определяют также центральные моменты третьего и четвёртого
порядка:

99
n
x–x
=M
3
i
3
∑
; (5.58)
n
x–x
=M
4
i
4
∑
, (5.59)
которые могут быть рассчитаны по значениям начальных момен-
тов
m
k
по формулам:
;m–= mM
2
122
(5.60)
;m2+mm3–= mM
3
12133
(5.61)
.m3–mm6+mm4–= mM
4
1
2
2
1
31
44
(5.62)
Вычисляют коэффициент асимметрии и эксцесс:
;/MA = M
2/3
23
(5.63)
3–/ME = M
2
2
4
,
(5.64)
а также их среднеквадратичные отклонения, соответственно, S
А
и S
Е
:
)3)(n +1(n +
)1n(n – 6
=S
A
; (5.65)
.
)5)(n +3(n +)1–(n
)3–)(n2–n(n24
=S
2
E
(5.66)
Приведенные формулы (5.63) – (5.66) позволяют вычислять ста-
тистические оценки
А, Е, S
А
, S
Е
, которые для выборок небольшого
объёма являются смещёнными.
Несмещённые оценки для показателей асимметрии и эксцесса
определяют по формулам:
� A
2–n
)1–n(n
=
A
1
; (5.67)
[]
6) E +1(n +
)3–)(n2–(n
1–n
=E
1
. (5.68)

100
Несмещённые оценки среднеквадратичных отклонений для этих
показателей вычисляют по формулам:
)3)(n1)(n2–(n
)1–n(n6
=S
1
A
++
; (5.69)
)5)(n +3)(n +2–)(n3–(n
)1–n(n24
=S
2
E
1
. (5.70)
Основными показателями точности измерений являются стан-
дартная ошибка (стандарт)
S и дисперсия S
2
.
В генеральной совокупности или выборках большого объёма
практически все случайные ошибки измерения ограничены по аб-
солютной величине значения
±3σ (правило трёх сигм). При нор-
мальном распределении применяют также следующие показатели
точности измерений:
вероятная ошибка
ρ = 0,674σ; (5.71)
средняя абсолютная ошибка
САО =
= 0,7979σ
;
π2
2
σ
(5.72)
мера точности
σ
I
= 0,7071
2σ
I
h =
. (5.73)
5.5.2 Обнаружение грубых ошибок (промахов)
В специальной литературе можно встретить различные реко-
мендации для обнаружения грубых погрешностей измерений и от-
сева промахов.
Если имеется выборка небольшого объёма
n, то можно восполь-
зоваться методом сравнения максимального относительного от-
клонения |x
i
– x
|
max
/S с критическим (при выбранном уровне зна-
чимости и числе степеней свободы f = n – 2), значение которого
определяют по таблице.
Здесь мы впервые сталкиваемся с понятием о статистической
гипотезе.
