Peube J-L. Fundamentals of fluid mechanics and transport phenomena
Подождите немного. Документ загружается.


Thermodynamics of Discrete Systems 23
by any homogenous function S of degree 1. For example, for a fluid, the following
relation can be written:
NpVTSE
P
Differentiating relation [1.13] or [1.14], and comparing with expression [1.10] or
[1.11], we obtain the relations:
(Gibbs Duhem relation)
ii
i
SdT+ X dY =0 -
¦
[1.15]
0
1
¸
¸
¹
·
¨
¨
©
§
¦
i
ii
dZX
T
Ed
[1.16]
1.3.1.3.
The equations of state
An expression relating the extensive and the intensive quantities which
characterize a system is habitually called an
equation of state
.
The intensive variables, being by definition partial derivatives of a function
,...),(
XSE
, are not independent. In practice we rarely use the general equation of
state [1.6], which only relates the extensive quantities, using instead the more usual
equations of state which relate extensive and intensive variables, which can be more
or less dependent.
For example, for a perfect gas, we know that there are two equations of state:
dTmCdENRTpV
v
These are not independent as the first equation of state implies that the specific
heat
C
v
can only be a function of the temperature (Joule’s law; see elementary works
on thermostatics).
1.3.2. Thermodynamic potentials
1.3.2.1.
Introduction
While the preceding presentation assigns a particular role to the extensive
variables, using them to represent a given system does not lead to the most useful
means of studying that system. The temperature or pressure of a fluid are of a more
direct interest than its volume or its energy when it comes to isobaric or isothermal
processes. We often prefer a combination of intensive and extensive variables for
studying a given system. From a mathematical point of view, such changing of
24 Fundamentals of Fluid Mechanics and Transport Phenomena
variables can be relatively complex (e.g. contact or Legendre transformations [IGO
89], [COU 89], [BYU 02]).
Let us consider a simplified situation comprising a function
),( yxf in two
variables. Instead of taking the couple (x,y), we take the new variables ( yfx ww /,):
we thus replace the variable y with the derivative yf ww / , the function f not being
known a priori. We cannot therefore hope to obtain the explicit properties, only
those of the differentials being accessible. We thus perform a change of function,
replacing the differential of the extensive variable with the differential of the
conjugate intensive variable. The simplest example is the introduction of the
enthalpy H:
pVEH(p,S,N)
For a fluid, the differential dH can be written:
dNTdSVdppVEddH
P
whence we see the intensive variable p appears in differential form. This is
particularly convenient for the study of isobaric transformations or shaft work.
1.3.2.2.
Definition of thermodynamic potentials
The preceding method is a general one. Suppose for instance that we want to
choose the collection of independent variables (
ji
YX ,
)
2
: we define the function
ji
YXE ,:
¦
j
jjji
YXEYXE ,
Using relation [1.10]
3
the differential of the function
ji
YXE ,
can be written
as:
¦¦¦
j
jj
i
ii
j
jjjj
dYXdXYdXYdYXdEEd [1.17]
The function
E
is a thermodynamic potential whose partial derivatives:
2 The subscripts i and j correspond respectively to the different couples of extensive and
intensive variables.
3 Here, S is included in extensive variables X and is not explicitly written.

Thermodynamics of Discrete Systems 25
kj
Y
i
X
k
k
Y
E
X
z
¸
¸
¹
·
¨
¨
©
§
w
w
,
with respect to the intensive variables Y
k
, are the corresponding extensive variables
4
.
Using this expression in the definition of
E
, we obtain the Gibbs-Helmholtz
relation (a partial differential equation for
E
as a function of E):
EY
Y
E
E
j
j
j
w
w
¦
[1.18]
Remember that we frequently use:
– the
Helmholtz function
NTVF
,, (free energy);
,,
hence:
with:
FVTN E TS
dF pdV SdT μdN
FF F
pS μ
VT N
ss s
ss s
– the
Gibbs function
NTpG
,, (free enthalpy):
,,
hence:
with:
GpTN E pV TS
dG Vdp SdT μdN
GGG
S μ
p
TN
sss
sss
V
The thermodynamic potentials are first order homogenous functions which
satisfy Gibbs-Duhem relations (section 1.3.1.2). They are useful for the study of
systems where certain intensive variables remain constant.
4 Notation
k
j
Y
i
X
k
Y
z
ww
,
specifies that the chosen independent variables are X
i
and Y
j
.
26 Fundamentals of Fluid Mechanics and Transport Phenomena
For example, during a constant-pressure (p
a
) evolution of a system whose
volume increases by an amount
'
V, the system receives an amount of work
Vp
a
' . from the exterior. If W denotes the work (aside from that due to the
pressure p
a
), the variation of enthalpy
'
H of the system is (section 1.3.2.1):
QWVpEVpEH
aa
'' ' ' ..
[1.19]
Generally speaking, the source of an extensive quantity X
j
, for which the
intensive variable Y
j
is constant, providing the system with 'X
j
by means of a quasi-
static process, leads to a variation of its thermodynamic potential equal to:
QWXYEE
jj
'' '
(
W and Q being respectively the work and heat received from means other than the
source, with Y
j
being constant).
1.3.2.3.
Thermostatics and variables change
The traditional practical problem of thermostatics consists of passing from a
representation of a system with n variables to another representation with n variables
related to the first by means of conjugation properties in the entropic and energetic
representations. The number of possible combinations of n independent variables
among the 2n extensive or intensive variables is clearly large. It is in fact the
principal practical difficulty of thermodynamics. This multiplicity of possible
independent variables leads to the numerous Maxwell relations between the
coefficients of the differential forms of energy, entropy, enthalpy and the different
thermodynamic potentials; the general form can be written by means of the
differential
Ed
[1.17]:
i
j
j
j
i
i
i
i
i
j
j
i
Y
X
Y
X
X
Y
X
Y
Y
Y
X
X
w
w
w
w
w
w
w
w
w
w
w
w
'
'
'
'
We will leave it to the reader to work out examples involving the explicit
functions given below.
Remember the rules for changing variables when using partial derivatives: if the
three variables (x,y,z) are related, it is straightforward to show that:
11
¸
¸
¹
·
¨
¨
©
§
w
w
¸
¸
¹
·
¨
¨
©
§
w
w
¸
¸
¹
·
¨
¨
©
§
w
w
¸
¸
¹
·
¨
¨
©
§
w
w
¸
¸
¹
·
¨
¨
©
§
w
w
z
z
yx
z
x
y
y
x
x
z
z
y
y
x
[1.20]
Thermodynamics of Discrete Systems 27
1.3.2.4.
“Thermodynamic” coefficients
For quasi-static closed process (N=const) we define the coefficients using units
of mass or of volume. The specific heats at constant volume C
v
and at constant
pressure C
p
, and the calorific coefficients h and l are:
dphdTNMCdVldTNMCTdSdQ
pv
from which we can derive the relations:
2
2
,
2
2
,
T
G
NM
T
T
S
NM
T
C
T
F
NM
T
T
S
NM
T
C
Np
p
NV
v
w
w
¸
¸
¹
·
¨
¨
©
§
w
w
w
w
¸
¸
¹
·
¨
¨
©
§
w
w
[1.21]
NVNT
T
p
T
TV
F
T
V
S
Tl
,
2
,
¸
¸
¹
·
¨
¨
©
§
w
w
ww
w
¸
¸
¹
·
¨
¨
©
§
w
w
[1.22]
NPNT
T
V
T
TP
G
T
P
S
Th
,
2
,
¸
¸
¹
·
¨
¨
©
§
w
w
ww
w
¸
¸
¹
·
¨
¨
©
§
w
w
[1.23]
In general, depending on the thermodynamic transformations studied, we may
choose diverse independent variables. For example, we define the calorific
coefficients
O
and
P
:
dvdpTdSdQ
P
O
and the isothermal and adiabatic compressibility coefficients, respectively
F
T
and
F
S
:
S
S
T
T
p
V
Vp
V
V
¸
¸
¹
·
¨
¨
©
§
w
w
¸
¸
¹
·
¨
¨
©
§
w
w
11
FF
[1.24]
Recall the Reech relation (not derived here):
J
F
F
V
p
S
T
C
C
28 Fundamentals of Fluid Mechanics and Transport Phenomena
The speed of sound is defined by the relation (
U
being specific mass):
S
SN
p
c
UFU
1
2
¸
¸
¹
·
¨
¨
©
§
w
w
[1.25]
The coefficients of dilatation are defined by the relations:
VT
F
pT
p
ppT
G
VT
V
V
VP
ww
w
¸
¸
¹
·
¨
¨
©
§
w
w
ww
w
¸
¸
¹
·
¨
¨
©
§
w
w
22
11
;
11
ED
[1.26]
We recall the usual relations, which the reader can verify using identities [1.20]:
T
C
T
T
C
s
c
p
ssp
c
V
T
NMC
p
T
NMC
T
V
NM
T
p
C
T
p
NM
T
V
C
T
p
T
V
NM
T
CC
p
p
p
pp
p
p
V
v
p
T
p
V
T
v
Vp
vp
UDUUUU
J
D
E
PO
U
¸
¸
¹
·
¨
¨
©
§
w
w
¸
¸
¹
·
¨
¨
©
§
w
w
¸
¸
¹
·
¨
¨
©
§
w
w
¸
¸
¹
·
¨
¨
©
§
w
w
¸
¸
¹
·
¨
¨
©
§
w
w
¸
¸
¹
·
¨
¨
©
§
w
w
¸
¸
¹
·
¨
¨
©
§
w
w
¸
¸
¹
·
¨
¨
©
§
w
w
¸
¸
¹
·
¨
¨
©
§
w
w
¸
¸
¹
·
¨
¨
©
§
w
w
¸
¸
¹
·
¨
¨
©
§
w
w
¸
¸
¹
·
¨
¨
©
§
w
w
;;
;;;
;;
22
2
2
2
2
We deduce from this that the differential of the specific entropy (per unit mass) s
as a function of the dp and d
U
variables can be written in one of the following forms:
U
E
U
UDE
UU
U
UU
dcdp
pT
C
d
T
C
dp
pT
C
dcdp
p
s
d
s
dp
p
s
ds
v
p
v
p
2
2
¸
¸
¹
·
¨
¨
©
§
w
w
¸
¸
¹
·
¨
¨
©
§
w
w
¸
¸
¹
·
¨
¨
©
§
w
w
[1.27]
1.3.2.5.
Perfect gas
Consider a perfect gas with constant specific heats
v
C
and
p
C
and of molar mass
M. By reasoning using the unit of mass, state relation [1.6] between the extensive
quantities can be written:

Thermodynamics of Discrete Systems 29
1
1
const exp const
with: ; ;
v
v
es
sCLn e
C
mV NM V s Sm e Em h Hm
¬
¬
®
®
From the intensive variable definitions, we can easily derive the usual state
equations:
const with: . joule/mole
v
prT eCT Rr
U
0
We can thereby obtain expressions for the extensive variables as functions of
other variables, (
e
0
, h
0
, s
0
) being some constants:
00
1
0
1
0000
;
1
;
1
s
p
LnCs
p
T
LnCs
T
LnCs
h
p
hTChe
p
eTCe
vpv
pv
¸
¸
¹
·
¨
¨
©
§
¸
¸
¹
·
¨
¨
©
§
¸
¸
¹
·
¨
¨
©
§
JJJJ
UU
UJ
J
UJ
in addition to expressions for the usual coefficients given below:
.;
;;
1
;
1
;
2
J
FUJ
U
J
ED
U
vpvp
S
CCrCC
rT
p
c
T
hpl
[1.28]
1.4. Out-of-equilibrium states
1.4.1. Introduction
The reasoning of section 1.2.2.4 shows how a system which is not in equilibrium
does not have a general state relation outside of equilibrium conditions. The
extensive quantities remain defined, but they are no longer sufficient to characterize
the state of the system, as the entropy can no longer be defined as a function of these
parameters alone. As seen in section 1.2.2.4, the distribution of extensive variables
is uniquely defined for a system in equilibrium, whereas this is no longer the case
for a system which is not in equilibrium: a more detailed description of the structure
of the system is thus necessary. This implies that
more parameters will be necessary
a priori for a description of an out-of-equilibrium system than for one which is in a
state of equilibrium.
30 Fundamentals of Fluid Mechanics and Transport Phenomena
The general method for describing an out-of-equilibrium system involves
considering the system
as a collection of sub-systems, each of which is in a state of
equilibrium
and which can thus be described by means of their extensive variables.
We suppose (postulate) that such a procedure is always possible.
As the system is no longer in equilibrium, exchanges occur between the
extensive variables of the various sub-systems, and the intensity of these exchanges
must be characterized. It is now essential that time be homogenous, in other words,
for an out-of-equilibrium system whose characteristics do not change, the amounts
of quantities exchanged must be proportional to the duration of the transfers. At this
point, it is sufficient to consider continuous matter at rest, i.e. in a fixed reference
frame.
1.4.2. Discontinuous systems
1.4.2.1. General principles
A real system nearly always comprises a continuous variation of its physical
properties. We therefore represent the latter using piecewise constant functions
defined on a partition of the system in
P sub-systems, each of which is
approximately in a state of equilibrium
, and to which we can therefore apply the
properties of systems in equilibrium. Let
k be the number of independent extensive
variables required for a description of each sub-system (number of moles, volume,
energy, entropy, etc.) in terms of an energetic or entropic representation.
A
knowledge of the state of the system S requires a complete description of the P
sub-systems, i.e. a total of
kP variables. As seen earlier, certain extensive variables
can be replaced by their corresponding intensive variables, which are defined for
each sub-system as a result of the hypothesis that these sub-systems are in a state of
equilibrium. This of course does not change the total number of independent
variables,
kP. For each sub-system p, we have the entropic form of the general
equation of state (the energy of each sub-system, which is not individualized here, is
included in the variables
X
i
):
kiPpXSS
ippp
,...,1;,...,1
where
X
ip
designates the extensive quantity X
i
contained in the sub-system p.
The
extensive quantities of the complete system can be obtained by adding the
corresponding extensive quantities of the sub-systems:
),...,1(;
11
PpXSSXX
P
p
ipp
P
p
ipi
¦¦

Thermodynamics of Discrete Systems 31
Note that in general, it is obviously not possible to obtain a relation between the
extensive quantities
X
i
of a system and its entropy S, since the kP variables X
ip
must
be eliminated from the
k + 1 preceding equations. This fact bears witness to the
absence of a general equation of state for an out-of-equilibrium system.
The extensive quantities
X
i
are generally functions of time. The flux
M
ip
of the
quantity
X
i
received by the component p is defined by:
dt
dX
ip
ip
M
The origin of the quantities
dX
ip
and the flux
M
ip
can be considered individually
for each of the sub-systems. Let
dX
ip,q
(resp. dX
iq,p
) be the amount of extensive
quantity
X
i
received by the sub-system p (resp. q) from the sub-system q (resp. p) in
time
dt. The amount of entropy dS
p,q
(resp. dS
q,p
) received by each of the systems
and associated with the aforementioned transfer is evaluated by means of the
entropic representation differential of each of the sub-systems:
¦¦
k
i
piqiqpq
k
i
qipipqp
dXZdSdXZdS
1
,,
1
,,
The intensive variables
Z
ip
and Z
iq
of two neighboring sub-systems will have
different values if the sub-systems are not in equilibrium, and so the entropy
variations
dS
p,q
and dS
q,p
will have different absolute values. Indeed, there can only
be an exact balance between the two sub-systems if the intensive variables
Z
ip
and
Z
iq
are equal.
With the exception of entropy, “exchanged” quantities obey the principle of
action and reaction which results from the conservation principles (section 1.2.2.3):
0
,,,,
t
pqqppiqqip
dSdSdXdX
[1.29]
During an irreversible transfer of an extensive quantity, the entropy gained by a
body is greater than the entropy lost by the body from which the extensive quantity
is transferred
(this statement is algebraically true).
The distribution of intensive variables is thus a constant function of space within
the spatial bounds of a given sub-system, discontinuities at the frontier of each sub-
system existing in proportion to the degree of thermodynamic imbalance within the
system. Such imbalance leads to an exchange of the quantities
dX
ip,q
between the
sub-systems. It is thus necessary to introduce
relations between these causes and
32 Fundamentals of Fluid Mechanics and Transport Phenomena
their effects. Before dealing with the general problem of these relations, we will
illustrate the methodology using the following elementary example, comprising two
sub-systems which only exchange heat between themselves, or with the exterior.
1.4.2.2.
An insulated thermal system
1.4.2.2.1. Entropy variation
The simplest example is an ensemble which is insulated from the exterior
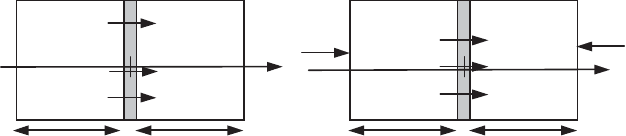
(Figure 1.6a), comprising two conducting blocks separated by a diathermic wall
which creates a resistance to heat transfer (thermal resistance). Each of the subs-
systems is, by assumption, characterized by its calorific energy content
Q
1
(resp. Q
2
)
or its temperature
T
1
(resp. T
2
), assumed to be uniform at every instant. These
quantities vary slowly with time on account of the thermal resistance of the system.
AA
(a) (b)
T
1
T
i
T
2
x
O
M
1e
M
2e
M
T1,2
M
T2,1
T
1
T
i
T
2
A
x
O
A
M
T1,2
M
T2,1
Figure 1.6.
Heat transfer in an (a) insulated or (b) uninsulated system
The ensemble is not in equilibrium and is thus subject to a natural evolution
during which the entropy increases, while the internal energy remains constant. We
will calculate the variation in entropy between the state thus defined and the
equilibrium state.
The entropy of a solid mass
m of constant specific heat capacity C is
const; SmCLnT
the entropy of the ensemble of the two blocks, which are
assumed to be identical, is thus:
12 12
constSS S mCLnTT
As the ensemble is insulated from the exterior, the total amount of heat remains
constant:
12
constmCT mCT
