Peube J-L. Fundamentals of fluid mechanics and transport phenomena

Подождите немного. Документ загружается.

Physics of Energetic Systems in Flow 103

As in Chapter 1, we will begin by considering the simplest discrete system

having mechanical properties: the material particle or the material point. This choice

is made on account of the fact that a geometric point suffices to define its position.

A material system, like any thermodynamic system, is made up of many simple

systems, each comprised of an ensemble of material particles. These are described

by systems whose dimensions are sufficiently small.

The extensive quantity associated with the motion of a material particle is

momentum. The momentum of a material system is the sum of the momentum of its

components. This vector quantity is proportional to the extension of the particle.

The momentum of an isolated mechanical system remains constant.

3.1.3. Momentum and velocity

As space is homogenous, the momentum of an isolated system is a function

neither of its coordinates nor of time. Its expression must be identical in all Galilean

reference frames; this property will impose an expression for the momentum.

We must note firstly that the idea of entropy does not exist in the mechanics of a

particle. It only appears for systems in which the thermodynamic properties are

defined and in which mechanical energy is transformed into heat. We will come

back to this point a little later (section 3.2.5).

The intensive quantity associated with the momentum, for an elementary system,

is the velocity

with components u

, which represents the intensity of motion in a

Galilean reference frame. Velocity depends on the reference frame used.

In a Galilean reference frame, momentum can only be a function of velocity in

that reference frame, and not of position or time. The relationship between

momentum and velocity can be derived from the preceding principles.

In effect, consider an isolated system composed of

two identical particles. These

particles, of constant initial velocities

and

in a Galilean reference frame R,

interact through a collision (whose details are not important) such that after the

collision they have the same constant velocity '

(a soft impact) in this same

reference frame. If





is the momentum of each particle, the momentum

conservation of the two particle system can be written in R as:













VpVpVp



104 Fundamentals of Fluid Mechanics and Transport Phenomena

This equality must be true in all Galilean reference frames moving with constant

velocity

having any value) with respect to the reference frame R. The

following identity is derived, true for all













VVVpVVpVVp

GGG

  '2

This equality implies that the function





is a linear function (take V

successively equal to



and '

 , and then derive the identity













YXpYpXp

  , characteristic of a linear relationship).

The momentum of a particle can thus be written in the form:

Vmpump

jiji

where

m is a constant tensor which characterizes the material particle. As space is

isotropic, this tensor is necessarily spherical (

ijij

A material particle is thus characterized by a scalar

m (mass) which leads to the

relation:

)( Vmpumump

iijiji

[3.1]

Similar reasoning using a Lorentz group for changing reference frames leads to a

different expression of mass in special relativity.

3.1.4. Definition of force

As momentum is an extensive quantity it must satisfy a balance equation. When

a material particle is subjected to an external action, its momentum changes. We call

this external action

force f

; it constitutes a source of momentum for this particle,

whose rate of change

is:

[3.2]

Physics of Energetic Systems in Flow 105

Forces are independent of the Galilean reference frame chosen for their

description (this is no longer true in relativistic mechanics).

The effect of a force during a time interval (

) is characterized by a vector

equal to the momentum variation

between these two instants. This is, by

definition, the

impulse

received by the particle:

pdtfI

[3.3]

The idea of an impulse is useful in the study of collisions, which are often very

rapid events and the detailed modeling of which is replaced by more or less global

assumptions regarding their nature (soft impact, elastic, etc.). The

external force

acting on a material particle is the

impulse quantity

received by the particle per

unit time.

As for the other thermodynamic quantities, this definition is only of interest in so

far as we are able to explain the expression of this force as a function of external

parameters. As with the other thermodynamic quantities, we can distinguish:

–

volume forces

representing actions at a distance, which are due to force fields:

gravity, electromagnetic forces, etc.;

–

contact forces

, due to interactions on the microscopic scale between molecules,

ions, atoms, etc. As for other contact actions, these are modeled by

surface forces

stresses, pressure, viscous or dry friction, etc. We will come back to this point in the

sections covering continuous media.

NOTES

–

1) A force is associated with the material element on which it acts: forces are

localized vectors (bi-points in mathematics) which can only be composed for each

application point considered separately, except in the case of a rigid solid.

2) Forces are actions which obviously exist independent of motion.

106 Fundamentals of Fluid Mechanics and Transport Phenomena

3.1.5. The fundamental law of dynamics (closed systems)

Consider a closed material particle, i.e. one that does not exchange matter with

the exterior; its mass is thus constant. Substituting [3.1] into [3.2] we obtain:





Vmd

[3.4]

This equation, called the

fundamental law of dynamics

(or

Newton’s second law

of motion

), involves the acceleration ;

Ȗ dV / dt

the quantity

is called the

quantity of acceleration.

The quantity of acceleration is only the momentum’s time derivative for systems

of constant mass. A rocket which ejects a certain momentum in order to propel itself

is not a closed system. In fluid mechanics, we will often reason in terms of open

systems which exchange momentum with the exterior.

3.1.6. Kinetic energy

Every extensive quantity has a corresponding form of energy. The term for the

energy differential (kinetic energy

) associated with the extensive quantity

for

the preceding system’s motion is:

iic

dpudE

[3.5]

which, taking account of expression [3.1] for a

particle of constant mass m

, is:

ddumudE

iic

[3.6]

Kinetic energy can thus be expressed by the relation:

Physics of Energetic Systems in Flow 107

The kinetic energy theorem can be obtained by taking the scalar product of the

two sides of equation [3.2] with the velocity V

[3.7]

The quantity

is the power of the force

in the reference frame considered.

As with the kinetic energy, it depends on the reference frame used for its evaluation.

3.2. Mechanical material system

3.2.1. Dynamic properties of a material system

A mechanical material system will be constructed, as for any thermodynamic

system, by decomposition into

sub-systems which are points (or nearly points) in

separate equilibriums (here at uniform velocity). The sub-systems interact amongst

themselves according to the principle of action and reaction which results from the

extensive nature of momentum. This quantity and the kinetic energy associated with

the movement for the whole system of points are additive:

¦¦

Epp

[3.8]

The conservative nature of extensive quantities entails that total momentum

remains constant in an isolated system. The velocity, which is the corresponding

intensive variable, is of course not defined for the complete system if this one is not

in a uniform state.

Quantity

is called the

total linear momentum

momentum

of the system.

also define the

total angular momentum

angular momentum

at a point O

the relation:



pOM

Introducing the inertia center of the material system, and using formula [3.1],

relation [3.8] can be written:

VmP

108 Fundamentals of Fluid Mechanics and Transport Phenomena

Internal actions between components of the material system balance one another

two by two like all internal actions. Let us separate the forces acting on the particle

into external forces

iext

and internal forces

int

representing interactions

between

and the other material particles of the system. Applying equation [3.2]

gives:

niFF

iiext

,.....2,1

int



[3.9]

The

vector equations [3.9] enable a detailed study of the mechanical system.

By taking their sum, we obtain a vector equation which eliminates the internal forces

and describes the effect of external action on the sum of the quantities of particle

acceleration

dtpdm

iii

in the system, which is called

dynamic

resultant

dtPdm

iextG

[3.10]

Equations [3.10] state that

the

dynamic resultant

dtPd

is equal to the sum of

the external forces

. Internal forces do not participate and the momentum of an

isolated system remains constant.

We proceed in similar fashion for the moments of the internal forces, which

cancel one another out, two by two; the moment

at a given point in the ensemble

of forces, naturally reduces to the moment of the external forces. The sum of the

moments of the quantities of acceleration

dtpd

at O, also called

dynamic moment

at a point

is equal to the sum

ext

of the moments of the external forces

acting on the points M

and considered at the same point

We know that in taking moments, either at a fixed point O, or at the inertia

center of the system, the dynamic moment

is equal to the time derivative of the

total angular moment

, this last moment being the sum of the momentum

moments:

iext

[3.11]

Physics of Energetic Systems in Flow 109

The conservation of linear momentum for an isolated system is thus a

consequence of the properties of internal forces.

Two particular vectors

and

define an entity which replaces the detailed

distribution of localized momentums only in the case of rigid solids. The reader

should refer to texts on mechanics for a further study [AME 58].

3.2.2. Kinetic energy of a material system

3.2.2.1.

Kinetic energy theorem

Kinetic energy theorem [3.7] is applied for each particle of the system. For the

material system it can be obtained by taking the sum of all the kinetic energy

equations corresponding to the particles

(obtained by taking the scalar product of

each equation [3.9] with

mecf

iic

PP 

int

[3.12]

with:



iif

intint

, the

power of the internal forces

;



iextimec

the power of the external forces

(mechanical power

provided to the mechanical system from the exterior).

The power of the internal forces is not generally zero.

3.2.2.2.

The power of internal forces

The power of internal forces is independent of the reference frame used for its

evaluation.

In order to show this, it suffices to regroup the internal forces by couples of

opposed forces

and

interacting between the points

and

. The work

of these forces is:



jiijijijijijijij

MMFMMFMFMFW

 

110 Fundamentals of Fluid Mechanics and Transport Phenomena

The two vectors of the scalar product

are independent of the reference frame

chosen (Galilean or otherwise) and the scalar

takes on the same value in all

reference frames; the same is true for the total work done by the internal forces. As

time is identical in all reference frames, the power of the internal forces is thus

independent of the reference frame used.

Certain internal forces derive from a potential, such as Newtonian forces or

elastic forces; the same is not true for frictional forces.

3.2.2.3.

The power of external forces

Let us consider a case where the

external forces

and certain internal forces

derive from a potential U

, the other internal forces being designated by

int

Equation [3.12] can be written:



¦¦



ifi

FVMiU

int

[3.13]

We define the

mechanical energy

of the system by the relation:





Equation [3.13] can be written:

intf

[3.14]

The total mechanical energy of the isolated material system is not conserved

because the internal forces provide a non-zero power, except in certain particular

cases (rigid, solid, etc.).

Consider the following example: two particles of the same mass m are elastically

linked with friction; they constitute an oscillator where each of their opposed

elongations are centered around the inertia center G.

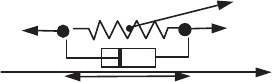
Physics of Energetic Systems in Flow 111

Figure 3.1. Isolated oscillator

We assume that there are no external forces. The kinetic energy of the whole is

the kinetic energy of the inertia center animated by the constant velocity V

, which

is increased by the kinetic energy of the oscillator in a reference frame related to the

inertia center G. The total mechanical energy can be obtained by adding the

potential energy of the oscillator. This decreases on account of the friction and is

transformed into heat, thus increasing the internal energy by heat addition. On the

other hand, the momentum of the ensemble has not changed.

The

power of the internal forces

depends only on the relative particle velocity

and

not on the chosen reference frame.

On account of the internal friction of the

system, it decays as well as the total mechanical energy of the system.

3.2.3. Mechanical system in thermodynamic equilibrium: the rigid solid

We will now examine how motion intervenes in thermostatics and

thermodynamics. Consider a material system, assumed to be in movement and

isolated, in other words not surrounded by any other material system which exerts an

action on it; it will finish by being “rigidified”: the relative movements of its

different constituents disappear under the effect of internal dissipative forces

(viscous damping or internal friction, exchange of momentum and collisions

between the particles comprising the system, etc.). In other terms, the relative

distances between the different material particles making up the system remain

constant. The mechanical system in thermodynamic equilibrium has become a

rigid

system

in which there are no longer any entropy sources associated with friction.

The system is in a state of thermostatic equilibrium if its other extensive quantities,

defining its internal state, are no longer susceptible to change.

We obtain the same final state for a material system placed in a force field

derived from a potential. The fluids contained in such a material system are thus in

hydrostatic equilibrium. We have already discussed, in section 2.2.1.2, the restrictive

conditions necessary for the existence of such a situation. However, if the external

force field does not derive from a potential, the exterior will always be able to

112 Fundamentals of Fluid Mechanics and Transport Phenomena

communicate an energy to compensate the friction to the fluid (by an

electromagnetic action in a conducting fluid, for example).

The rigid solid thus plays an important role from the point of view of

thermostatics, since it is the ultimate state (thermostatic equilibrium) towards which

all isolated mechanical systems will tend. It is furthermore what is observed for a

gaseous or liquid mass enclosed in a container which is not subject to any external

action; the same is true for all collections of solids (a pile of sand, etc.), including

solar bodies: the moon no longer rotates, always showing the same side to the Earth;

the daily rotation of the Earth slows continually due to diverse dissipative effects

(mostly tidal movements of the oceans, which lead to a dissipation of energy on

account of a gravitational Earth-sun and Earth-moon interactions).

We know that the momenta of a rigid solid are characterized by linear

momentum and angular momentum, which are constant for an isolated rigid solid.

Recall that its motion is not characterized by an instantaneous constant velocity

vector of rotation; (this motion is a Poinsot motion around its inertia center (see texts

on mechanics [AME 58])).

3.2.4. The open mechanical system

3.2.4.1.

Introduction

We can also perform a balance for an open material system whose momentum

varies because of an input of matter (for example a water bomber collecting water)

or an output of matter (the propulsion of a rocket). In fluid mechanics, the balances

of extensive quantities, including momentum, are performed for open systems.

However, the physical conservation laws for extensive quantities are applied to a

given material quantity, i.e. to closed systems. The balance equations for open

systems must obviously take account of the change of definition in the system where

the balance is performed (section 1.1.4.2), i.e. take into account the input or output

of extensive quantities associated with the input or loss of matter.

3.2.4.2.

Momentum of a rocket

As an example, consider the vertical motion of a rocket in a gravitational field.

Its mass

m(t)

decreases with the ejection of a constant mass flow of gas



at a velocity U with respect to the rocket.

Let

m(t)

be the rocket mass at instant

. We consider a fixed reference frame Oz

and perform an elementary momentum balance between time

and

t + dt

on the

mass

comprised by the rocket at time