Петросян Л.А. и др. Теория игр

Подождите немного. Документ загружается.

ГЛАВА II

БЕСКОНЕЧНЫЕ АНТАГОНИСТИЧЕСКИЕ ИГРЫ

§ 1. БЕСКОНЕЧНЫЕ ИГРЫ

1.1. В этой главе рассматриваются антагонистические игры,

которые отличаются от матричных тем, что в них один или оба

игрока имеют бесконечное (счетное или континуум) множество

стратегий. С теоретико-игровой точки зрения это отличие малосу-

щественно, поскольку игра остается антагонистической и проблема

состоит в использовании более сложного аналитического аппарата

исследования.

Таким образом, будем исследовать общие антагонистические

игры, т. е. системы вида

Г=(Х, Y, Н), (1.1)

где X

—

произвольные бесконечные множества, элементы кото-

рых являются стратегиями игроков 1 и 2 соответственно,

а Н: Хх.

Y-*R

— функция выигрыша игрока 1. Напомним, что

правила антагонистической игры изложены в п. 1.1 гл. 1. Выигрыш

игрока 2 в ситуации (х, у) равен

[—

Щх, у)], хеХ, yeY (игра

антагонистическая). В этой главе будем рассматривать такие игры,

у которых функция Н ограничена.

1.2. Пример 1.

(Одновременная игра преследования на плоскости.)

Пусть Si и S

— множества на плоскости. Игра Г заключается

в следующем. Пусть 1 выбирает некоторую точку

xeS

а игрок

2 — точку

yeS

При совершении выбора игроки 1 и 2 не имеют

информации о действиях противника, поэтому подобный выбор

удобно интерпретировать как одновременный. Точки

xeS

yeS

являются в этом случае стратегиями игроков 1 и 2 соответственно.

Таким образом, множества стратегий игроков совпадают с множе-

ствами S

и S

на плоскости.

Целью игрока 2 является минимизация расстояния между ним

и вторым игроком (игрок / преследует противоположную цель).

Поэтому под выигрышем Щх, у) игрока 1 в этой игре будем

понимать евклидово расстояние р(х, у) между точками xeSi

, т. е. Щх, у)=р(х, у), xeS

yeS

. Выигрыш игрока

полага-

ем равным выигрышу игрока 1, взятому с обратным знаком (игра

антагонистическая).

Пример 2. (Поиск на отрезке.) Простейшей игрой поиска с бес-

конечным числом стратегий является следующая игра.

Игрок 2 (прячущийся) выбирает точку у

[0,

1], а игрок 1 (ищу-

щий) выбирает одновременно и независимо точку хе[0, 1]. Точка

у считается «обнаруженной», если

\х—у\^1,

где

0</<1.

В этом

случае игрок 1 выигрывает величину +

во всех остальных случаях

его выигрыш полагается равным 0. Игра антагонистическая.

Таким образом, функция выигрыша имеет вид

fl, если |дс-.И</,

Н(х,у)

[О — в противном случае.

Выигрыш игрока 2 полагается равным

[—Н(х,

у)].

Пример 3.

(Поиск

на

сфере.)

Пусть в R

задана сфера С радиуса

Игрок 1 (ищущий) выбирает систему из точек x

, .... х,еС,

а игрок 2 — одну точку у е

С.

Выборы точек осуществляются игро-

ками одновременно и независимо друг от друга. Игрок 2 считается

обнаруженным, если точка уеС оказывается в r-окрестности одной

из точек

Xj,

j=\, ..., s. Здесь под г-окрестностью точки Xj будем

понимать сферический сегмент с вершиной в точке Xj и радиусом

основания г (рис. 2). В дальнейшем r-окрестность точки х

}

будем

обозначать через S(x

r).

Целью игрока 1 является обнаружение игрока

Игрок 2 пресле-

дует противоположную цель.

соответствии с этим положим выиг-

рыш игрока 1 равным

(l, если

уеМ

(

'У)

{

(О — в противном случае,

где x=(x

.... x

) и M

=\J S(xp r). Выигрыш игрока 2 полагается

равным

[—Н(х,

у)].

Пример

(Шумная дуэль.)

Каждому из двух дуэлянтов разреша-

ется выстрелить только один раз. Предполагается, что оба они

имеют «шумные» пистолеты, так что каждый знает, когда выстре-

лил его противник. Предполагается также, что функция меткости

Pi(x) (вероятность попадания при стрельбе в момент времени х)

игрока 1 определена на

[0,1],

непрерывна, монотонно возрастает по

(0)=0,Pi(l)=

Аналогично, точность выстрела игрока 2 опи-

сывается функцией р

(у) на [0, 1], где/>

(0) = 0,

(1)=1-

Если игрок

1 поражает игрока 2, то первый получает выигрыш +1; если игрок

2 поражает игрока /, то игрок 1 получает

—1,

если оба игрока

стреляют одновременно и с одинаковым результатом (успешным

или нет), то выигрыш игрока 1 равен 0.

Структура информации в этой игре (тот факт, что оружие шум-

ное) принимается во внимание при составлении функции вьшгрыша

Н(х, у). Если х<у, то вероятность того, что игрок / поразит

противника, равна р

(х) и выигрыш игрока / равен 1 р^х); вероят-

ность того, что игрок 1 промахнется, равна

\—р

(х).

Если игрок

2 еще не стрелял и знает, что игрок 1 больше не может выстрелить,

то игрок 2 будет увеличивать свои шансы на успех, ожидая, пока

у не станет равным 1. Таким образом, если игрок 1 промахнется

в момент х, то он наверняка будет поражен игроком 2, если х<у,

следовательно,

Щх, у)=/>

(х) + (-1)[1-/>

(х)], х<у.

Аналогично имеем

Щх.

У)=Рг<У)

-РгШ

•

*>У

Щх. у)=Р

(х)[1-р

(у)]+р

(у)[\-р

(х)](-1), х=у.

Таким образом, функция выигрыша Щх, у) в игре равна

Рис.2

Г2р

(х)-1,

х<у,

Щх,У)=<р

(х)-р

(у).х~у.

Ll-2p

(y),

x>y,

гдехе[0,

1],

уе[0, I].

Пример 5. (Бесшумная дуэль.) Снова

каждому из дуэлянтов разрешается вы-

стрелить только один раз, но в этом слу-

чае ни один из дуэлянтов не может опре-

делить, выстрелил его противник или нет.

Предположим для простоты, что фун-

кции меткости заданы следующим обра-

зом:

(x)=p

(x) =

Тогда функция выиг-

рыша, описывающая игру, имеет вид

х—

(1—

х)у, если х<у,

Н(х,у)=\о, если х=у,

.—

у+(1—

у)х, если х>у,

где хе[0,

1],

уе[0, I]. Построение функции выигрыша Щх, у) в этой

игре производится так же, как и в примере 4, за исключением того,

что в данном случае ни один из игроков не может определить

момента выстрела противника, если только этот выстрел не оказал-

ся успешным.

Пример 6. (Поиск

«шумного» объекта.)

Рассматривается задача

поиска «шумного» объекта (игрок 2) подвижным средством об-

наружения (игрок

1).

Дальность действия

1(х,

у) средства обнаруже-

ния в зависимости от скоростей хв[х

, xj и уе\у

, у J игроков

1 и 2 соответственно имеет вид

где

1(у) =

Р(у-Уо),

(11-1о)1(У1-Уо),

li=bi), 1

=Ъо)- Поло-

жительные числа

считаются заданными. Таким

образом,

У)= •

(Vi-^o)

(*i-*o)

В качестве функции выигрыша Щх,

у)

игрока

понимается произ-

водительность поиска,

т. е.

просмотренная площадь

единицу

времени

Н(х,

y)=2xl(x,

у).

Выигрыш игрока

полагаем равным

[—Н(х,

у)].

Таким образом, получаем игру

функцией выигрыша

b>i-y)+li(y-yo)

(*i-*)

Н(х, у)=2х

(У1-Уо) (Xi-x

)

тяе

хе[х

Ху],

уе\у

уД.

13.

заключение отметим специальный класс антагонистичес-

ких игр,

которых

Х=

У=[0, 1]. В этих играх ситуации суть пары

чисел

(х, у), где х, уе[0, 1]. Эти

пары задают точки единичного

квадрата. Поэтому такие игры называются играми

на

единичном

квадрате.

Класс игр на единичном квадрате во многом характеризу-

ет бесконечные антагонистические игры

поэтому является базо-

вым при исследовании бесконечных игр. В частности, примеры 2,

S — примеры игр

на

единичном квадрате. Пример

также игра

на

единичном квадрате, если положить х

=у

=0, x

СИТУАЦИЯ 8-РАВНОВЕСИЯ, 6-СЕДЛОВЫЕ ТОЧКИ

И 6-ОПТИМАЛЬНЫЕ СТРАТЕГИИ

2.1.

Как и во

всякой антагонистической игре

Г=(Х, Y, Н),

в бесконечной игре принципом оптимального поведения игроков

является принцип равновесия. Оптимальной (равновесной) является

такая ситуация (х*, у*), для которой выполняются неравенства

Щх,

у*)

< Щх*,

у*)

< Щх*,

у) (2.1)

при всех

хеХ, yeY.

Этот принцип реализуется

игре

Г в том

и только

том случае, когда

v = v = v,

«=max

inf

Щх, у),

(2.2)

* У

«=min sup H(x,

у),

т.

е.

внешние экстремумы максимина

минимакса достигаются

и нижнее значение игры v равно верхнему значению v. Такая ан-

тагонистическая игра Г называется вполне

определенной,

а число

v — значением игры (см. п. 3.4 гл. I).

Для матричных игр существование и равенство максимина ми-

нимаксу было доказано в классе смешанных стратегий (см. § 6 гл.

I),

поэтому решение игры заключалось в нахождении их общего

значения v и тех стратегий х*. у*, на которых достигаются внешние

экстремумы в (2.2).

Для бесконечных игр существование внешних экстремумов

в (2.2), вообще говоря, не обязательно.

2.2.

Пример 7. Пусть, каждый из игроков 1 а 2 выбирает

число из открытого интервала (0, 1), после чего игрок 1 получает

выигрыш, равный сумме выбранных чисел. Таким образом, по-

лучаем игру на открытом единичном квадрате с функцией вы-

игрыша Н(х, у) игрока 1

Щх, у)=х+у, хе(0, 1), уеф, 1). (2.3)

Здесь ситуация (1, 0) была бы равновесной, если бы 1 и 0 входили

в число стратегий игроков, а значение игры

было бы v

дейст-

вительности внешние экстремумы в (2.2) не достигаются, а верхнее

и нижнее значения игры равны между собой. Поэтому »=1и игрок

выбирая число 1-е, е>0, достаточно близкое к 1, всегда может

получить выигрыш, достаточно близкий к значению игры. С другой

стороны, игрок 2, выбирая число е>0 достаточно малым (близким

к 0), может гарантировать, что его проигрыш будет сколь угодно

близким к значению игры.

23.

Определение.

Ситуация

(х„ у,) в

антагонистической

игре

Г=(Х, Y, Н)

называется ситуацией

е-равновесия,

если для любых

стратегий

хеХ и yeY

игроков

1 и 2

соответственно выполняется

неравенство

Н(х, у.)-в^Н(х„ у.)^Н(х„ у) + Е. (2.4)

Точка (х„ у,), для которой имеет место (2.4), называется е-

седловой

точкой,

стратегии

х, и у, —

е-оптимальными

стратеги-

ями

игроков

1 и 2

соответственно.

Полезно сравнить определения ситуации равновесия (2.1) и е-

равновесия

(2.4).

Если отклонение от оптимальной стратегии приво-

дит лишь к уменьшению выигрыша этого игрока, то отклонение от

е-оптимальной стратегии может привести к его увеличению, но не

более чем на е.

Так, ситуация (1-е, е),

0<е<1,

является е-равновесной в приме-

ре 7, а стратегии х,=

—е,

у,=Е — е-оптимальными стратегиями

игроков 1 и 2 соответственно.

2.4. Заметим, что для двух стратегически эквивалентных игр

Г=(Х Y, Н) и r=(Z, Y, Н), где Н'

рН+а, /?>0, справедливы

следующие результаты. Если

(х

}>„)

— ситуация е-равновесия в игре

Г, то она является ситуацией (/?е)-равновесия в игре Г' (ср. с леммой

о масштабе

3 гл. I).

2.5.

Основное свойство е-оптимальных стратегий дает следу-

ющая теорема.

Теорема. Для того чтобы supinfH(x,y) =

х у

= inf sapH(x,y)=v< +

оо,

необходимо

достаточно,

чтобы

для лю-

у *

бого

е>0

существовали

е-оптимальные

стратегии х„

у,

игроков 1

и 2,

при

этом

lim

Щх„,

)=v.

(2.5)

в-»0

Доказательство. Необходимость. Пусть игра Г имеет ко-

нечное значение v. Для любого е>0 выберем стратегию у, из

условия

sup Н(х, у,)- е/2 <й (2.6)

хеХ

и стратегию х, из условия

infH(x

,y) + e/2>v. (2.7)

yeY

Из (2.2), (2.6), (2.7) получаем неравенство

Н(х,

у.)

- в/2 ^ v < Щх„ у) + в/2 (2.8)

для всех стратегий х, у. Следовательно,

\H(x

,yJ-v\^B/2. (2.9)

Из неравенств (2.8), (2.9) следуют соотношения (2.4), (2.5).

Достаточность. Если для любого числа е>0 выполняются

неравенства (2.4), то

sup inf Н(х, у)=inf sup H(x, y) = v<

+ ao

х у ух

«=inf sup H(x, j>)<sup H(x,

j>„)

<#(*.,

у,)

+ е^

у х

< inf

Н(х„

у) + 2е ^

sup

inf Щх, у) +

2е=v+2e.

(2.10)

у х у ~

Отсюда заключаем, что

ю<ю,

но согласно лемме п. 2.2 гл. I справед-

ливо противоположное неравенство. Таким образом, остается до-

казать, что значение игры Г конечно. Возьмем такую последовате-

льность

{£„},

что lim £„=0. Пусть

е{в„},

£*

„е{£

}, где т — любое

Л-.00

фиксированное натуральное число. Имеем

(

'к+т>

У'к)+

к+т>Щх,

к+т

Уе

к+т

)>Щх

Вк

У.

к+т

)-В

к+т

(*«*.

J4+J

+.Ь>Н(х.

)>H(x

tk+m

Вк

)-г

Таким образом, \Н(х,

у,

)-Н(х

$к+т

ек+т

)\^е

+г

к+т

кт

Так как

lim Shn = 0 при любом фиксированном значении т, то существует

к->аа

конечный предел lim H(x

, у

). Из соотношения (2.10) получаем

«-•о

неравенство

\Н(х„

у,)—v\^s,

следовательно, v = lim H{x

, y

). Teope-

«-.0

ма доказана.

2.6.

Для иллюстрации приведенных в этом параграфе определе-

ний рассмотрим подробно пример

п. 1.2.

Пример 8. Предположим, что множества S

и S

представляют

собой замкнутые круги с радиусами ^ и R

fi?

<i?

). Найдем

нижнее значение игры

«=max min p(x, у).

xeS

yeS

Пусть

XQGS^

Тогда min p(x

, у) достигается в точке у

пересече-

ния прямой, проходящей через центр О

круга S

и точку х

с границей круга S

. Очевидно, что величина min p(x

, у) достигает

максимального значения в точке

MeS

являющейся точкой пересе-

Рис.

чения линий центров ОО

(рис. 3) с границей круга S

наиболее

удаленной от точки О

Таким образом, v

M\ —

Для вычисления верхнего значения игры

t5=min max р(х, у)

рассмотрим два случая.

Случай

Центр О круга S

принадлежит множеству S

(рис. 4).

Для каждого y

точка х

, доставляющая max р(х, у

), строится

xeS

следующим образом.

Пусть Хо и х§ — точки пересечения прямой О{у

с границей

круга S

a xl — точка пересечения прямой Оу

с границей круга S

наиболее удаленная от точки у

. Тогда х

определяется из условия

р(х

,у

)=т&х pfx'o.yj.

По построению, для всех у

е S

max p(x, y

)=p(x

Уо)^^.

Однако при

получаем

max p(x, 0)=R

xeS

поэтому

min max p(x, у) =v=R

yeS

xeS

Непосредственно видно, что, поскольку

OeS

в случае

1 v=R

^\O

M\—R

=v. При этом равенство возможно лишь при

условии, что О принадлежит границе множества S

Таким образом, если в случае

точка О не принадлежит границе

множества S

, то значения игры и ситуации равновесия не существу-

ет. Если же точка О принадлежит границе множества S

, то суще-

ствует ситуация равновесия, при этом оптимальная стратегия игро-

ка 1 заключается в выборе точки М, лежащей на пересечении линии

центров ОО

с границей множества S

и наиболее удаленной от

точки О

. Оптимальная стратегия игрока 2 заключается в выборе

точки

yeS

совпадающей с центром О круга S

. Значение игры при

этом равно v=v=v =

—

Случай 2. Центр круга

ОфБ

Этот случай рассматривается как

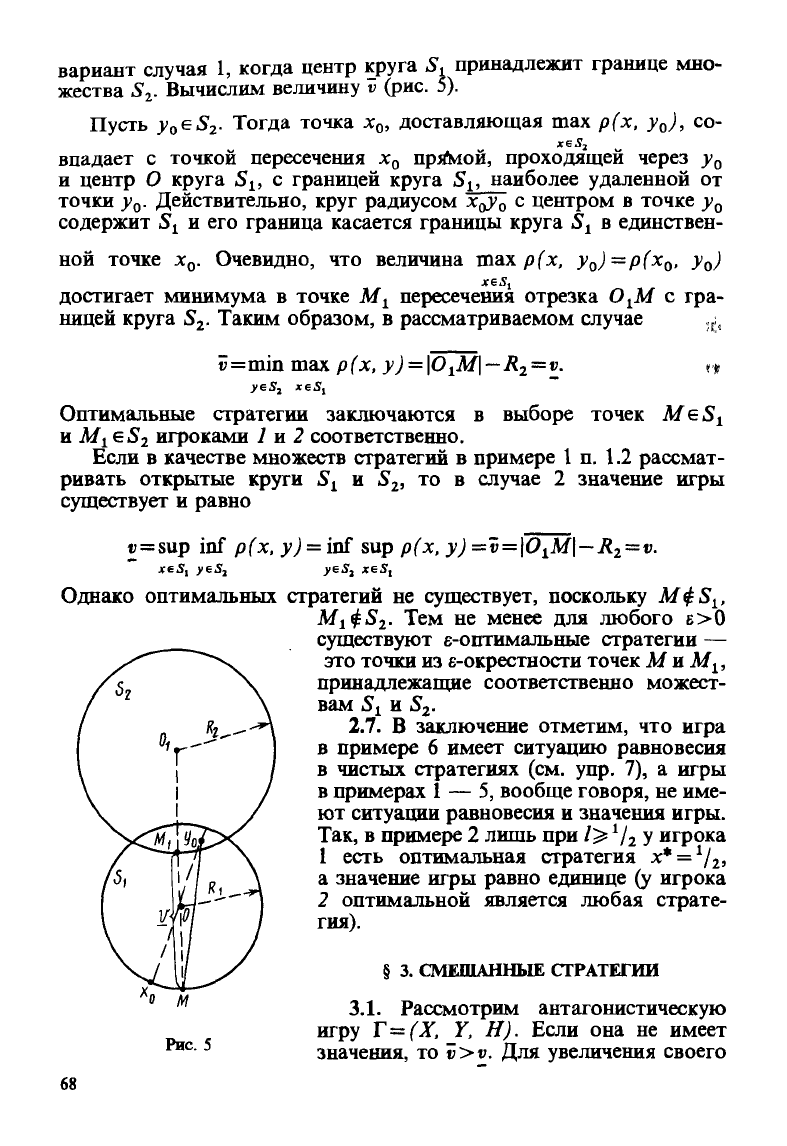
вариант случая 1, когда центр круга S. принадлежит границе мно-

жества S

. Вычислим величину v (рис. 5).

Пусть y

. Тогда точка х

, доставляющая max p(x, у

), со-

дсе5

впадает с точкой пересечения л:

прямой, проходящей через у

и центр О круга S

с границей круга S

наиболее удаленной от

точки у

. Действительно, круг радиусом

ХоУ

с центром в точке у

содержит 5

и его граница касается границы круга S^ в единствен-

ной точке х

. Очевидно, что величина max р(х, у

)=р(х

, у

)

дсеЯ,

достигает минимума в точке М

пересечения отрезка О^М с гра-

ницей круга S

. Таким образом, в рассматриваемом случае ,,;,

v=minmax p(x, y)

M\—R

=v.

Оптимальные стратегии заключаются в выборе точек MeSi

и M

игроками 1 и 2 соответственно.

Если в качестве множеств стратегий в примере 1 п. 1.2 рассмат-

ривать открытые круги 5

и S

, то в случае 2 значение игры

существует и равно

« = sup inf p(x, y) = iaf sup p(x, у) =v

M\ —

= v.

xeS

yeSj yeS,

xeS

Однако оптимальных стратегий не существует, поскольку МфБ

фБ

. Тем не менее для любого Б>0

существуют е-оптимальные стратегии —

это точки из е-окрестности точек М и M

принадлежащие соответственно можест-

вам 5

и S

2.7.

В заключение отметим, что игра

в примере 6 имеет ситуацию равновесия

в чистых стратегиях (см. упр. 7), а игры

в примерах

— 5, вообще говоря, не име-

ют ситуации равновесия и значения игры.

Так, в примере 2 лишь при /^

у игрока

1 есть оптимальная стратегия

х*

а значение игры равно единице (у игрока

2 оптимальной является любая страте-

гия).

§ 3. СМЕШАННЫЕ СТРАТЕГИИ

3.1.

Рассмотрим антагонистическую

игру Т=(Х, Y, Н). Если она не имеет

значения, то v>v. Для увеличения своего

гарантированного выигрыша в таких случаях каждому игроку, как

уже отмечалось в § 4 гл. I, важно знать намерение противника.

И хотя правила игры не представляют такой возможности, при

достаточно частом повторении игры

одним и тем

же

противником

можно статистически оценить возможность выбора той или иной

стратегии и поступить определенным образом. Как же должен

поступить игрок, не желающий, чтобы его намерение было рас-

крыто? Единственным разумным способом в этом случае является

выбор стратегии случайным образом, в соответствии с определен-

ным случайным механизмом, т. е. необходимо использовать сме-

шанные стратегии.

Дадим формальное определение смешанной стратегии для бес-

конечной игры.

3.2. Пусть х — некоторая а-алгебра подмножеств множества

X (включающая в себя одноточечные множества хеХ) и v — о-

алгебра подмножеств Y (yev, если yeY). Обозначим через

и У

множества всех вероятностных мер на ег-алгебрах х и v соот-

ветственно, и пусть функция Н измерима относительно <т-алгебры

Рассмотрим интеграл

K(li, v) = [ [н(х, y)dn(x)dv(y),

fieX,

ve ?, (3.1)

X Y

представляющий собой математическое ожидание выигрыша Н(х,

у) по мерам ц, v [85].

Определение.

Смешанным расширением

игры Г=(Х, Y, Н)

называется антагонистическая

игра в

нормальной

форме с множе-

ствами стратегий

X, Y и

функцией выигрышей

К(ц, \), т. е. игра

Г=(Х,?,К).

Поведение игроков в смешанном расширении игры Г можно

интерпретировать следующим образом. Игроки выбирают незави-

симо друг от друга меры цеХ и veY. В соответствии с этими

мерами они реализуют (например, с помощью таблицы случайных

чисел) случайный выбор стратегий хеХ и ye Y. После этого игрок

J получает выигрыш Н(х, у). Стратегии цеХ, veY называются

смешанными,

а хеХ, yeY

— чистыми стратегиями

в игре Г.

Введение смешанного расширения бесконечной игры требует определенных пояс-

нений. Множества 2

Т зависят от

того,

на каких (7-алгебрах

рассматриваются

вероятностные меры.

случае матричных игр (множества X

Y конечны) в смешан-

ном расширении игроки выбирали свои стратегии согласно вероятностным рас-

пределениям на множествах X и Y. Бели X

—

бесконечное множество и мы будем

поступать так же, как в конечном случае, то необходимо рассматривать меры, для

которых измеримы все подмножества бесконечного множества X. Однако таких мер

сравнительно

мало:

это меры, сосредоточенные на не более чем счетных множествах

точек. Используя только такие меры, игроки обедняют свои возможности (и далеко

не всегда могут гарантировать существование ситуации равновесия в смешанных

стратегиях). Поэтому используют менее обширные ^-алгебры, на которых определя-