Pelliccione M., Lu T.-M. Evolution of Thin Film Morphology: Modeling and Simulations

Подождите немного. Документ загружается.

3.1 General Characteristics 31

To make the connection between a self-aﬃne surface and a fractal, we

present a general introduction of fractal behavior. We can deﬁne a fractal for

our purposes as follows. If we are interested in ﬁnding the area of an object

in two dimensions, we can cover the object with small patches of linear size

l and count how many patches it takes to fully cover the object. If we found

that it takes N patches to cover the object, the area of the object would be

the number of patches used times the area of each patch, which would be

A = Nl

. (3.5)

We can do the same thing in one and three dimensions, and denoting this

embedding Euclidean dimension by d, the “area” would satisfy

A = Nl

, (3.6)

where “area” in one dimension is length, and “area” in three dimensions is

volume. Because we are dealing mainly in two dimensions, we continue with

the concept of area. If we repeat this procedure with diﬀerent size patches by

changing l, we will ﬁnd that the number of patches we use to cover the surface

is related to the size of the patch as

N(l) ∼ l

−D

, (3.7)

where D is the fractal dimension of the surface. For ordinary surfaces, the

fractal dimension D is equal to the embedding Euclidean dimension d because

the area does not depend on the size of the coverings used to measure it. For

example, in two dimensions, a square of side length L can be covered with

smaller squares of side length l<L. The number of smaller squares N(l)

required to cover the large square satisﬁes N(l)l

= L

, which implies that

N(l) ∼ l

−2

, and the Euclidean dimension is equal to the fractal dimension.

A fractal is a surface where the surface area one measures depends on the

size l of patches used to measure it. The area of the square in the previous

example did not change when the patch size changed; it remained constant

at L

. However, there are surfaces where the area measured depends on the

length scale used to measure it, and self-aﬃne surfaces belong to this class of

surfaces.

To show that self-aﬃne surfaces behave as fractals, we can write the surface

area of a thin ﬁlm described by the height proﬁle h(x)as

A =





1+|∇h(x)|

dx. (3.8)

However, for a self-aﬃne surface that obeys (3.1), if l is the size of the patch

being used to measure the surface area, then

|∇h(x)|≈

h(x + l) − h(x)

∼

∼ l

α−1

. (3.9)

32 3 Self-Aﬃne Surfaces

Because 0 ≤ α ≤ 1, if l is small, then l

α−1

will be very large, and the argument

of the integral for the surface area can be approximated as

A ≈



|∇h(x)|dx ∼



α−1

dx ∼ l

α−1

, (3.10)

where the integral



dx does not depend on l. From (3.6) and (3.7), this gives

A ∼ l

α−1

∼ l

−D

, (3.11)

which implies that D = d +1− α. Therefore, for a surface with α =1,the

fractal dimension and embedding Euclidean dimension are equal. However,

if α<1, the surface area measured depends on the size of the patch used

to measure it. From (3.10), the area depends on the size l of the patch as

A ∼ l

α−1

, so the smaller the size of the patch, the larger the measured area!

The most commonly cited real-world example of this phenomenon is the mea-

surement of the length of a coastline. If you measure the length of the east

coast of the United States with a ruler on a map, you will measure a much

smaller distance than if you walked the east coast with a ruler, measuring the

coastline along the way. The smaller the device, or “patch”, you use to mea-

sure the length of the coastline, the larger the length you will measure because

larger measuring devices miss the detailed structure of the coastline that ﬁner

measuring devices catch. This behavior is why the deﬁnition of the surface

slope in Sect. 2.6 diverges when α = 1. The derivative of the height proﬁle

is not well deﬁned in a continuum sense because the value of the derivative

depends on the length scale used to measure it. In other words, the limit

lim

l→0

h(x + l) − h(x)

, (3.12)

that is used to deﬁne the derivative, behaves as l

α−1

, which becomes inﬁnite

if α<1. As previously discussed, there is a cutoﬀ length scale a beneath

which the surface is no longer self-aﬃne, so the divergence of the derivative is

simply a result of discussing surface statistics in the limit as a → 0, which does

not hold for realistic surfaces. However, when applying continuum statistics

such as the autocorrelation function and height–height correlation function

to self-aﬃne surfaces, the continuum approximation can be used to obtain a

value for the local slope m, and the deﬁnition of the local slope m in (3.1) is

discussed in Sect. 3.3.

3.2 Lateral Correlation Functions

When the surface height proﬁle obeys (3.3), the correlation functions have

similar scaling properties. For small r, substituting (3.1) into the deﬁnition of

the height–height correlation function from (2.9) yields

3.2 Lateral Correlation Functions 33

H(r)

H(r) ~ r

2®

r ~ »

H(r) ~ 2w

Fig. 3.2. Representative height–height correlation function obtained from a simu-

lated self-aﬃne surface. The plot is on a log–log scale, which gives the height–height

correlation function a linear behavior for small r with slope 2α.

H(r)=



|h(x + r) − h(x)|



∼



|(mr)



∼ (mr)

2α

. (3.13)

It follows that the height–height correlation function behaves as

H(r) ∝



(mr)

2α

,r ξ,

,r ξ.

(3.14)

For a self-aﬃne surface, the height–height correlation function H(r) can be

expressed in the scaling form

H(r)=2w





, (3.15)

where the function f behaves as

f(x)=



2α

,x 1,

1,x 1.

(3.16)

This behavior is seen in Fig. 3.2, which depicts a representative height–height

correlation function for a self-aﬃne surface. Note that the height–height cor-

relation function for small r behavesasapowerlaw.

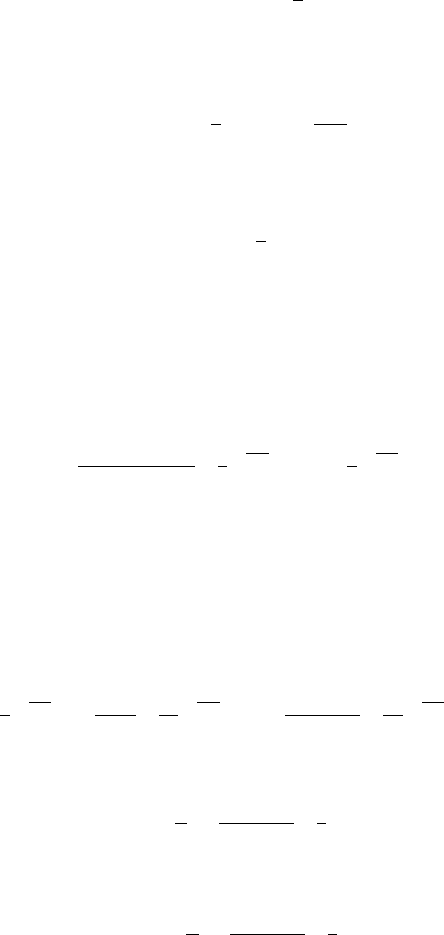
34 3 Self-Aﬃne Surfaces

Several analytic forms for the height–height correlation have been proposed

that satisfy the requirements for a self-aﬃne surface given in (3.14). For an

isotropic self-aﬃne surface, Sinha et al. [142] proposed the functional form

H(r)=2w



1 − exp



−





2α



. (3.17)

This form satisﬁes (3.14) because an expansion of the exponential for r  ξ

gives

H(r) ≈ 2w



1 −



1 −





2α



≈

2α

∼ r

2α

From (2.10), this implies that the autocorrelation function R(r)canbeex-

pressed as

R(r)=exp



−





2α



. (3.18)

We refer to this model as the exponential correlation model. Unfortunately,

using the exponential correlation model for R(r) does not work as α → 0be-

cause the autocorrelation function becomes constant when α = 0, which does

not reﬂect the required behavior of the function for a self-aﬃne surface. To

remedy this, a more complicated autocorrelation function has been proposed

[118] called the K -correlation model,

R(r)=

α−1

Γ(α +1)



√

2α





√

2α



, (3.19)

where Γ(x) is the gamma function and K

(x)istheα-order modiﬁed Bessel

function of the second kind. The gamma function and modiﬁed Bessel function

of the second kind are discussed in App. A.

Let us verify that the K -correlation model satisﬁes the properties required

of the height–height correlation function of a self-aﬃne surface given in (3.14).

From Sect. A.1.3, for r  ξ and 0 <α<1, the modiﬁed Bessel function of

the second kind behaves as



√

2α



∼

Γ(α)



2ξ

√

2α



−α

−

Γ(1 − α)

2α



2ξ

√

2α



Using this result, the autocorrelation function behaves as

R(r) ≈ 1 −





Γ(1 − α)

Γ(1 + α)





2α

It follows that the height–height correlation function behaves as

H(r) ≈ 2w



1 −



1 −





Γ(1 − α)

Γ(1 + α)





2α



∼ r

2α

3.2 Lateral Correlation Functions 35

(a)

(c)

x =r/»

-100

-50

® =0.01

Exponential Model

K-Correlation Model

x =r/»

-4

-2

(d)

(b)

x =r/»

® =0.75

x =r/»

-1

R(x)

® =1.00

-1

R(x)

® =0.25

R(x)

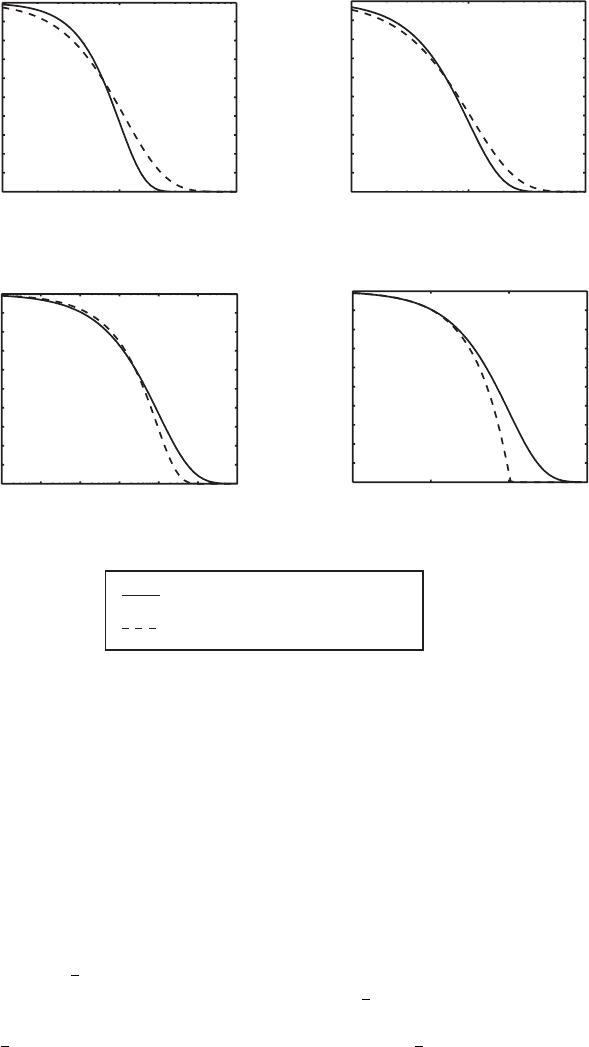
Fig. 3.3. Comparison of two proposed forms of the autocorrelation function for

a self-aﬃne surface given in (3.18), the exponential model, and (3.19), the K -

correlation model. Each plot has a diﬀerent value of α,(a) α =1.00, (b) α =0.75,

In addition, because K

(x) has an exponentially decaying behavior for large

x, H(r) ≈ 2w

for r  ξ. Therefore, (3.19) is a valid autocorrelation function

for a self-aﬃne surface. The advantage of this form of the autocorrelation

function is that it possesses an analytic Fourier transform, and thus its PSD

can be expressed in terms of elementary functions.

A comparison of the exponential correlation model given in (3.18) and

the K -correlation model in (3.19) is pictured in Fig. 3.3 for various values

of α.Forα>

,theK -correlation model approaches zero more gradually

than does the exponential model, and for α<

,theK -correlation model

approaches zero more abruptly than the exponential model. A crossover occurs

at α =

because the two models are equal when α =

, which follows from

36 3 Self-Aﬃne Surfaces

the representation of the modiﬁed Bessel function of the second kind

1/2

(x)=



−x

and the value of the gamma function, Γ





√

π/2. Keep in mind that the

exponential model and K -correlation model are only models for the correlation

functions, and any height–height correlation function that satisﬁes (3.14) may

be considered as a model [119, 120].

3.3 Local Slope

In the previous section, it was shown that the small r behavior of the height–

height correlation function is

H(r) ∼ (mr)

2α

, for r  ξ, (3.20)

which depends on the local slope m. Motivated by this behavior, we can deﬁne

the local slope as

2α

≡



−2α

H(r)



r=0

=2w



−2α

(1 − R(r))



r=0

, (3.21)

where (2.10) was used to relate the height–height correlation function to the

autocorrelation function. By dimensional analysis, we can deduce from this

expression that the local slope behaves as

m ∼

1/α

, (3.22)

because the height–height correlation function has units of w

, and is mul-

tiplied by a distance to the power −2α. Using (3.21), if the autocorrelation

function R(r) ≈ 1 − cr

2α

for small r, the local slope m is given by

m =(2w

1/(2α)

. (3.23)

With this result, the exponential model from (3.18) gives a local slope of

m =

√

1/α

, (3.24)

whereas the K -correlation model in (3.19) gives a local slope of

m =

√

1/α





Γ(1 − α)

Γ(1 + α)



1/(2α)

. (3.25)

Note that the local slope in both cases behaves as (3.22).

In Sect. 2.6, the RMS surface slope  of a surface was given as

3.4 Power Spectral Density Function 37





|∇h(x)|



. (3.26)

From the deﬁnition of a self-aﬃne surface given in (3.1), this equation can be

expressed as



∼ lim

r→0





h(x + r) − h(x)





∼ lim

r→0



|(mr)



∼ lim

r→0

2α

2α−2

. (3.27)

If α<1, the deﬁnition of the slope as  in (3.26) will diverge. From the

discussion of the behavior of  in Sect. 2.6, it follows that

2α

∼ lim

r→0

2−2α



∼−w



2−2α

∇

R(r)



r=0

. (3.28)

This expression relates the local slope m to the surface slope . One can also

take this expression as a deﬁnition of the local slope m, which may diﬀer by a

constant factor from (3.21). If the surface is isotropic in 2+1 dimensions, this

expression becomes

2α

∼−w



2−2α





R(r)



r=0

. (3.29)

This expression is consistent with (3.21) in 2+1 dimensions by adding a factor

of 2α

2α

= −

2α



2−2α





R(r)



r=0

, (3.30)

which can be shown by substituting the form R(r) ≈ 1 −cr

2α

, and comparing

to (3.23).

3.4 Power Spectral Density Function

The PSD of a self-aﬃne surface can be quantiﬁed by its asymptotic behavior,

as was discussed for the height–height correlation function in Sect. 3.2. The

PSD can be expressed as

P (k)=

(2π)



R(r)e

ik·r

dr, (3.31)

where k = |k| and r = |r| for an isotropic surface. Using one of Green’s

identities over the closed volume Σ, which is a generalization of integration

by parts in arbitrary dimensions,

38 3 Self-Aﬃne Surfaces



ψ(r)∇

φ(r)dr =



∂Σ

ψ(r)

∂φ(r)

∂n

dS −



∇ψ(r) ·∇φ(r)dr.

If we take ψ(r)=R(r)andφ(r)=−k

−2

ik·r

, this expression becomes



R(r)e

ik·r

dr =



∂Σ

R(r)

∂

∂n



−

ik·r



dS +



∇R(r) ·



ike

ik·r



dr.

In the limit of an inﬁnite domain, R(r) → 0 and the surface integral vanishes,

which gives for the behavior of the PSD,

P (k) ∼ w



∇R(r)e

ik·r

dr.

The presence of the autocorrelation function in this expression separates the

integral into two regimes, r ≤ ξ and r>ξ. Because R(r) is signiﬁcant only

for r ≤ ξ, we can approximate this integral as

P (k) ∼ w



∇R(r)e

ik·r

d−1

dr. (3.32)

The volume element in d dimensions dr is proportional to r

d−1

dr. In a rough

approximation, for large k ·r, the exponential oscillates much faster than the

rest of the integrand, which has the eﬀect of averaging the integral out to

zero for large k · r. Thus, the integral is cut oﬀ when k · r ∼ kr ≈ 1, and

the integration is signiﬁcant only over the domain r ∈ [0,k

−1

]. In the regime

where k  ξ

−1

, the domain [0,k

−1

] cuts oﬀ the domain of integration in

(3.32), which gives



k  ξ

−1



∼ w



−1

∇R(r)r

d−1

dr.

If we change to the dimensionless variable x = rξ

−1

, this integral becomes



k  ξ

−1



∼ w

kξ



(kξ)

−1

∇R(x)x

d−1

dx.

To obtain this form, recall that the gradient also introduces a factor of ξ,

∇

R(r)=ξ

−1

∇

R(x). For a self-aﬃne surface, ∇R(x) ∼∇H(x) ≈ x

2α−1

ˆx

when x  1. The PSD then behaves as



k  ξ

−1



∼

kξ



(kξ)

−1

2α+d−2

∼

kξ



2α+d−1



(kξ)

−1

∼ w

(kξ)

−2α−d

. (3.33)

3.5 Dynamic Scaling 39

For small k, k  ξ

−1

, we can no longer use (3.32) because of the factor of k

−1

in front of the integral and we go back to (3.31). The exponential restricts the

domain to r ∈ [0,k

−1

], however, this is less restrictive than r ∈ [0,ξ] for small

k,whichgives



k  ξ

−1



∼ w



R(r)r

d−1

dr ∼ w

. (3.34)

This result is independent of k, and the behavior of ξ can be found through

dimensional analysis; the autocorrelation function is dimensionless, and the

integral has dimensions of length to the power d. We can summarize these

results by expressing the PSD of a self-aﬃne surface in a scaling form,

P (k)=w

g(kξ), (3.35)

where

g(x) ∝



1,x 1,

−2α−d

,x 1.

(3.36)

Using the form of the autocorrelation function given by the K -correlation

model in (3.19), the PSD of a self-aﬃne surface in 2+1 dimensions can be

modeled as

P (k)=

2π



2α



1+α

. (3.37)

The mathematics of calculating this form of the PSD are given in Sect. A.4.2.

The asymptotic behavior of the PSD is given by, for k  ξ

−1

P (k) ≈

2π



2α



1+α

∝ k

−2−2α

. (3.38)

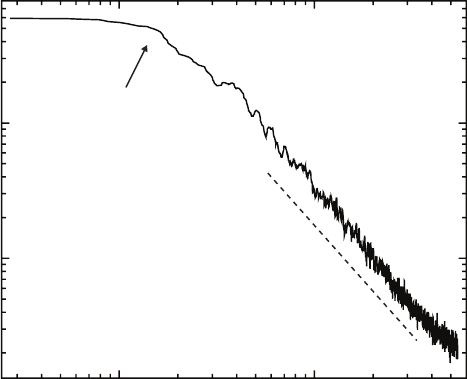
This behavior is seen in Fig. 3.4. Note that the PSD has no characteristic

peak, which allows for the scaling deﬁnition of a self-aﬃne surface [187]. A

characteristic peak in the PSD implies that there is a characteristic length

scale on the surface that will change upon rescaling, breaking the scaling

behavior of the surface. Because self-aﬃne surfaces have no such peak in their

PSD, the scaling deﬁnition holds.

3.5 Dynamic Scaling

A surface proﬁle is said to exhibit dynamic scaling if the surface height proﬁle

can be scaled in time. For a self-aﬃne surface, this gives [8, 40, 41, 104]

h(x, t) ∼ ε

−α

h(εx, ε

t), (3.39)

40 3 Self-Aﬃne Surfaces

P(k)

P(k) ~ k

-2®-2

k ~ »

-1

Fig. 3.4. Representative power spectral density function (PSD) obtained from a

simulated self-aﬃne surface in 2+1 dimensions (d = 2). The PSD spectrum exhibits

no characteristic peak.

where z is the dynamic exponent. The 1+1 dimensional form of the height

proﬁle has been used for simplicity, the same concept can be extended to

2+1 dimensions. If this scaling in time holds, increasing the time by a factor

ε increases the horizontal length scale by a factor ε

1/z

. Thus, the lateral

correlation length, which is a function of the horizontal correlations on the

surface, must evolve as

ξ(t) ∼ t

1/z

. (3.40)

Similarly, increasing the time by a factor ε changes the vertical length scale

by a factor ε

α/z

. The interface width is a function of the vertical height proﬁle

of the surface, therefore the interface width must evolve as

w(t) ∼ t

α/z

. (3.41)

Dynamic scaling predicts an interesting behavior for the time evolution of the

surface. All parameters that measure the surface are related to one another,

because the surface proﬁle scales as a whole in time. In particular, since the

surface grows on a substrate of ﬁnite linear size L, there is a natural bound on

the growth of the lateral correlation length because surface heights cannot be

correlated beyond the size of the substrate L. This implies that there exists a

crossover time t

where the lateral correlation length saturates, given by