Pelliccione M., Lu T.-M. Evolution of Thin Film Morphology: Modeling and Simulations
Подождите немного. Документ загружается.

This page intentionally blank

Part I
Description of Thin Film Morphology

2
Surface Statistics
Mathematically, rough surfaces can be described by a surface height profile
h(x,t), where h denotes the surface height with respect to the substrate at a
position x on the surface at time t. The functional form of h(x,t) implies that
there is only one surface height at position x, which may not hold for surfaces
with overhangs. In the discussion that follows, the surface height profile is
assumed to be a single-valued function.
To define the various statistics used to characterize rough surfaces, it is
convenient to define the concept of an average in this context. The average of
a function f(x,t), denoted as f(x,t), is defined as
f(x,t)≡
f(x,t)dx
dx
, (2.1)
where the domain of integration is the domain of the d-dimensional substrate,
and the vector x is d-dimensional. Surface growth is commonly referred to
as taking place in “d+1” dimensions, which means that the substrate is
d-dimensional, and the growth takes place in one extra dimension. For exam-
ple, growth on a two-dimensional substrate occurs in three dimensions because
the vertical growth of the surface occurs normal to the substrate. Growth in
2+1 dimensions is the most common experimentally as depositions usually
occur on a planar substrate. As such, we concentrate our discussion primarily
on 2+1 dimensions, although theoretical results are given for a general dimen-
sion d. It is noted that the general mathematical definition of average includes
a probability density function P (x,t) in the integrand. However, because all
surface heights are to be weighted equally, P (x,t) is constant in the domain
of integration and zero outside the domain, which is consistent with (2.1).
Also, if the domain is discrete rather than continuous, the integral can be
replaced by a discrete summation of all surface points. Measuring statistics
from a discrete surface is discussed in Sect. 2.9.
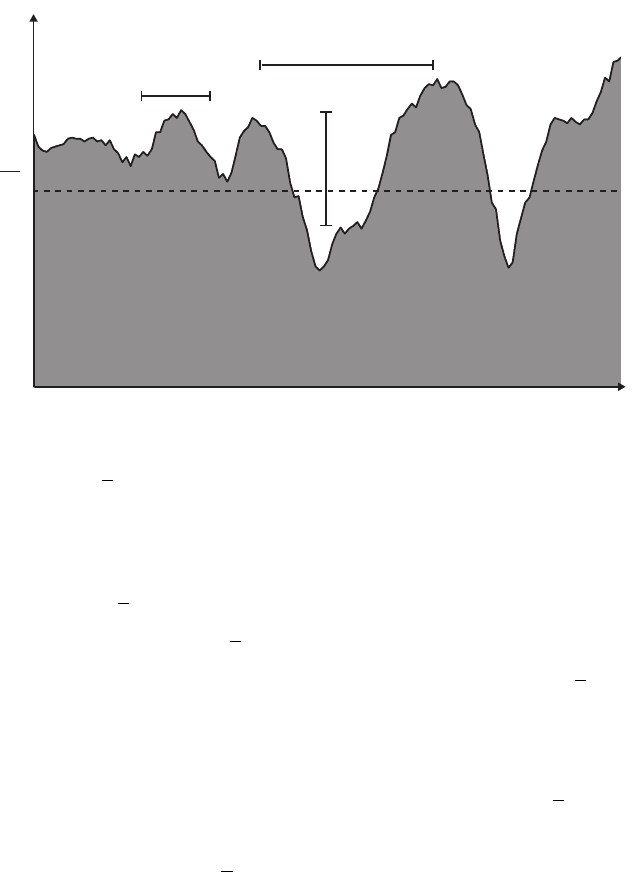
14 2 Surface Statistics
h(x)
x
h
w
»
¸
Fig. 2.1. Illustration of statistics used to describe rough surfaces. The definitions of
the mean height
h, interface width w, lateral correlation length ξ, and wavelength
λ are given in this chapter.
2.1 Mean Height
The mean height h of a surface profile is defined as
h(t) ≡h(x,t). (2.2)
It is very common to redefine the surface height profile such that
h =0
by choosing a suitable reference height. This is helpful when concentrating
on surface height fluctuations because any artificial effect introduced by the
mean height is removed. In the definitions that follow, the mean height is
taken to be equal to zero at all times. To obtain the definition for a surface
with a nonzero mean height, simply replace h(x,t)with(h(x,t) −
h). If the
reference height remains constant in time with respect to the substrate, and
if the flux of particles deposited on the surface is uniform in time, the mean
height will be linear in time,
h ∼ t, because the mean height is proportional
to the total number of particles deposited on the surface.
2.2 Interface Width
The most common statistic used to describe the roughness of a surface is the
standard deviation w of the surface heights, also called the interface width or
root-mean-square (RMS) roughness. The interface width is defined as

2.3 Autocorrelation Function 15
w(t) ≡
[h(x,t)]
2
. (2.3)
Larger values of the interface width indicate a rougher surface. It is common
to observe a power-law behavior for the interface width in deposition time,
w(t) ∼ t
β
, (2.4)
where β is referred to as the growth exponent. This characteristic behavior
of the interface width is the basis for dynamic scaling theory, which has been
widely used to describe the dynamic properties of thin films.
2.3 Autocorrelation Function
Statistics such as the mean height and interface width measure the vertical
properties of a surface and do not reflect correlations between different lat-
eral positions on the surface. To accomplish this, the autocorrelation function
R(r,t) is introduced, which measures the correlation of surface heights sepa-
rated laterally by the vector r. The autocorrelation function is defined as
R(r,t) ≡ w
−2
h(x,t)h(x + r,t). (2.5)
If the statistical behavior of a surface does not depend on the specific orienta-
tion of the surface, the surface is said to be isotropic, and the autocorrelation
function depends only on |r|. Thus, a new variable r = |r| can be introduced
to express the autocorrelation function as R(r, t). Surfaces that do not possess
this symmetry are called anistropic surfaces, whose treatment is not discussed
here. The interested reader may find more information about anistropic sur-
faces in [187].
General properties of the autocorrelation function can be deduced from
its definition. When r =0,R(0,t) = 1, using the definition of interface width
to evaluate the average. In addition, when r is large, surface heights become
uncorrelated. Because xy = xy if x and y are uncorrelated variables, for
large r,
R(r, t) → w
−2
h(x,t)h(x + r,t)∼w
−2
h
2
∼ 0, (2.6)
as the mean height
h is taken to be zero at all times by the choice of ref-
erence height. It follows that R(r, t) is a decreasing function of r, and how
fast R(r, t) decreases is a measure of the lateral correlation of surface heights.
For self-affine thin film surfaces, the autocorrelation function is often found
to have an exponentially decreasing behavior, which naturally satisfies the
above properties. Mounded thin film surfaces also exhibit a decreasing au-
tocorrelation function in general, but the autocorrelation function may also
exhibit oscillations as a result of the presence of mounds. Figure 2.2a shows the
characteristic behavior of the autocorrelation function of a self-affine rough
surface.

16 2 Surface Statistics
r
R(r)
1
»
0
e
-1
(a) (b)
0
2w
2
H(r)
r
Fig. 2.2. Plot of the general behavior of the (a) autocorrelation function and (b)
height–height correlation function for a self-affine rough surface. From (2.10), the
height–height correlation function is simply an inversion and vertical translation of
the autocorrelation function.
2.4 Lateral Correlation Length
Motivated by the properties of the autocorrelation function, the lateral cor-
relation length ξ is defined as the value of r at which R(r, t) decreases to 1/e
of its original value,
R(ξ, t) ≡ e
−1
. (2.7)
It follows that two surface heights are significantly correlated on average if
their lateral separation is less than the lateral correlation length ξ.Insome
contexts, continuum models for the autocorrelation function are used to de-
fine the correlation length that may differ from this definition. Regardless of
the specific definition, the correlation length must be measured in a consis-
tent manner to be meaningful. The time-dependent behavior of the lateral
correlation length is often found to be a power law,
ξ(t) ∼ t
1/z
, (2.8)
where z is referred to as the dynamic exponent.
2.5 Height–Height Correlation Function
A similar correlation function commonly used in scaling arguments is the
height–height correlation function H(r,t) defined as
H(r,t) ≡
(h(x + r,t) − h(x,t))
2
. (2.9)
The properties of H(r,t) can be inferred from the properties of the autocor-
relation function from the relation

2.6 Root-Mean-Square (RMS) Surface Slope 17
H(r,t)=
(h(x + r,t) − h(x,t))
2
=
[h(x + r,t)]
2
+
[h(x,t)]
2
− 2 h(x + r,t)h(x,t)
=2w
2
− 2
w
2
R(r,t)
=2w
2
[1 − R(r,t)] . (2.10)
From the properties of the autocorrelation function R(r,t), it follows that
H(0,t)=0andH(r, t) ∼ 2w
2
for r ξ. This behavior is seen in Fig. 2.2b.
As with the autocorrelation function, the height–height correlation function
is a function of r = |r| only for isotropic surfaces, which allows the height–
height correlation function to be expressed as H(r, t). The usefulness of this
new correlation function is in the behavior of the function for small r.For
most thin film surfaces, the height–height correlation function behaves as a
powerlawforsmallr, which obeys certain scaling properties as discussed in
Sect. 2.8.1.
2.6 Root-Mean-Square (RMS) Surface Slope
The root-mean-square surface slope is defined as
≡
|∇h(x,t)|
2
. (2.11)
Using integration by parts, (2.11) can be represented as
2
=
∇h(x) ·∇h(x)dx
=
h(x)
∂h(x)
∂n
dS −
h(x)∇
2
h(x)dx.
If the mean is taken to be zero at all times and the surface is isotropic, the
surface integral will average out to zero over a sufficiently large domain. If the
surface integral can be neglected, we find
2
= −
h(x)∇
2
h(x)dx
= −
h(x)
∇
2
r
h(x + r)
r=0
dx
= −∇
2
r
h(x)h(x + r)dx
r=0
= −w
2
∇
2
r
R(r = 0). (2.12)
In 1+1 dimensions, if the autocorrelation function is a function of r = |r| only,
this relation becomes

18 2 Surface Statistics
2
= −w
2
d
2
R(r)
dr
2
r=0
. (2.13)
In 2+1 dimensions, if the autocorrelation function is a function of r = |r| only,
this relation becomes
2
= −w
2
d
2
dr
2
+
1
r
d
dr
R(r)
r=0
. (2.14)
Applying this formula to a self-affine surface may lead to a divergence. The
local slope m can be introduced to remedy this problem; further discussion is
giveninSect.3.3.
2.7 Power Spectral Density Function
The lateral correlation length represents the short-range lateral behavior of a
surface, but beyond the lateral correlation length, even though surface heights
are not significantly correlated, they may exhibit a periodic behavior on a
length scale larger than the lateral correlation length. In order to deter-
mine this long-range behavior, the power spectral density function (PSD),
also known as the structure function, is used. The PSD is related to a d-
dimensional Fourier transform of the surface heights, defined in reciprocal
space as
P (k,t) ≡
1
(2π)
d
h(x,t)e
−ik·x
2
. (2.15)
To avoid confusion, we note that some authors use the variable q instead of k
in the definition of the PSD. To obtain an alternate representation of P (k,t),
expand (2.15) to give
P (k,t)=
1
(2π)
d
h(x,t)e
−ik·x
dx
h(x
,t)e
ik·x
dx
=
1
(2π)
d
h(x,t)h(x
,t)e
−ik·(x−x
)
dxdx
=
1
(2π)
d
h(r,t)h(r + r
,t)e
ik·r
drdr
=
1
(2π)
d
h(r,t)h(r + r
,t)dr
e
ik·r
dr
,
where the change of variables x = r and x
= r + r
was used and the
integration is over the entire domain of r and r
. Taking advantage of the
definition of the autocorrelation function from (2.5),
P (k,t)=
w
2
(2π)
d
R(r,t)e
ik·r
dr. (2.16)
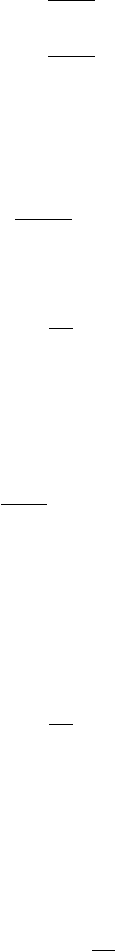
2.7 Power Spectral Density Function 19
The power spectral density function is a Fourier transform of the autocorre-
lation function. Using this definition, the total “area” in k-space enclosed by
the PSD is equal to w
2
,
P (k,t)dk =
w
2
(2π)
d
R(r,t)dr
e
ik·r
dk
=
w
2
(2π)
d
R(r,t)dr
(2π)
d
δ
d
(r)
= w
2
R(0,t)=w
2
, (2.17)
because R(0,t) = 1 by definition. The PSD can also be expressed in terms of
the height–height correlation function as
P (k,t)=
1
2(2π)
d
2w
2
− H(r,t)
e
ik·r
dr. (2.18)
To find the PSD of a 1+1 dimensional surface, take d = 1 and express the
PSD as
P (k, t)=
w
2
π
∞
0
R(r, t) cos(kr)dr, (2.19)
which follows because R(r) is even. To find the PSD of an isotropic 2+1
dimensional surface, take d =2andk · r = kr cos θ in polar coordinates.
For isotropic surfaces, P (k,t) depends only on k = |k|, so the PSD can be
expressed as P (k, t). The PSD can then be written as
P (k, t)=
w
2
(2π)
2
2π
0
∞
0
R(r, t)e
ikr cos θ
rdrdθ.
The angular integral can be evaluated to give
2π
0
e
ikr cos θ
dθ =2πJ
0
(kr),
where J
0
(x) is the zeroth-order Bessel function as discussed in Sect. A.1.1. It
follows that
P (k, t)=
w
2
2π
∞
0
R(r, t)rJ
0
(kr)dr, (2.20)
for an isotropic 2+1 dimensional surface. This form can be simplified by the
definition of a Hankel transform H,
H{R(r, t)}≡
∞
0
R(r, t)rJ
0
(kr)dr, (2.21)
which is discussed in Sect. A.3. The PSD then becomes
P (k, t)=
w
2
2π
H{R(r, t)}. (2.22)
20 2 Surface Statistics
If the PSD spectrum exhibits a characteristic peak at a wavenumber k
m
,
the surface possesses a long-range periodic behavior and is said to exhibit
wavelength selection at a wavelength
λ ≡ 2πk
−1
m
. (2.23)
Surfaces that exhibit wavelength selection are said to be mounded. If the PSD
exhibits a peak, the peak position k
m
generally has a power-law behavior in
time,
k
m
(t) ∼ t
−p
, (2.24)
where p is referred to as the wavelength exponent. Representative plots of the
PSD for different types of surfaces can be found in Fig. 3.4 on p. 40 and Fig.
4.5 on p. 54. In Fig. 3.4, the surface does not exhibit wavelength selection
because the PSD has no characteristic peak, whereas in Fig. 4.5 a peak is
clearly seen, which indicates that the surface is mounded.
2.8 Scaling
The concept of scaling is a powerful tool that allows for a considerable simplifi-
cation of the description of thin film rough surfaces. Scaling is often described
in terms of a scaling function that describes certain aspects of a rough surface.
There are two main types of scaling functions in this context: functions that
are invariant under scale transformations and functions that do not change
their characteristic behavior in time. These scaling concepts are very similar,
and are often both referred to simply as scaling. However, there are some key
differences in the behavior of these types of scaling and the physical results
they imply.
2.8.1 Self-Affine Scaling
Let a function f(x
1
,x
2
,...,x
n
) be a function of n variables x
i
, for example,
the surface height profile of a rough surface at some time t
0
. The function f
is said to exhibit self-affine scaling [100] if, for some function g(ε
1
,ε
2
,...,ε
n
),
f(ε
1
x
1
,ε
2
x
2
,...,ε
n
x
n
)=g(ε
1
,ε
2
,...,ε
n
)f(x
1
,x
2
,...,x
n
). (2.25)
This definition implies that if the variable x
i
has been rescaled by a factor ε
i
,
the resulting function is a constant factor multiplied by the original function.
Note that this notion of scaling is a property of the function f only, and is
in no means related to the behavior of f at other times t. From (2.25), for a
single-variable function f(x),
f(abx)=g(ab)f(x);
f(abx)=g(a)f(bx)
= g(a)g(b)f(x).
