Pecharsky V.K., Zavalij P.Y. Fundamentals of Powder Diffraction and Structural Characterization of Materials
Подождите немного. Документ загружается.


Fundamentals of Powder Diffraction and Structural Characterization
xxiii
easy to navigate. All web links, found in the book, are included on the CD
and can be followed
by
simply clicking on them. Every link is current as of
January 2003. The compact disk is accessible using both Mac's and PC's,
and potential incompatibility problems have been avoided by using portable
document, HTML, and ASCII formats.
Many people have helped in a variety of ways in making this book. Our
appreciation and respect goes to all authors of books, monographs, research
articles,
websites and computer programs cited and used as examples
throughout this text. We are indebted to our colleagues, Professor Karl
Gschneidner, Jr. from Iowa State University, Professor Scott R.J. Oliver
from SUNY at Binghamton, Professor Alexander
Tishin from Moscow State
University, Dr. Aaron Holm from Iowa State University, and Dr. Alexandra
(Sasha) Pecharsky from Iowa State University, who read the entire
manuscript and whose helpful advice and friendly criticism made this book
better. It also underwent a common sense test thanks to Lubov Zavalij and
Vitalij Pecharsky, Jr. Some of the experimental data and samples used as the
examples have been provided by Dr. Lev Akselrud from L'viv State
University, Dr. Oksana Zaharko from Paul Scherrer Institute, Dr. Iver
Anderson, Dr. Matthew Kramer, and Dr. John Snyder (all from Ames
Laboratory, Iowa State University), and we are grateful to all of them for
their willingness to share the results of their unpublished work. Special
thanks are in order to Professor Karl Gschneidner, Jr. (Iowa State
University) and Professor
M.
Stanley Whittingham (SUNY at Binghamton),
whose perpetual attention and encouragement during our work on this book
have been invaluable. Finally yet importantly, we extend our gratitude to our
spouses, Alexandra (Sasha) Pecharsky and Lubov Zavalij, and to our
children, Vitalij Pecharsky, Jr., Nadya Pecharsky, Christina Zavalij, Solomia
Zavalij, and Marta Zavalij, who handled our virtual absence for countless
evenings and weekends with exceptional patience and understanding.
Vitalij
K.
Pecharsky
Ames, Iowa
January 2003
Peter
Y.
Zavalij
Binghamton, New York
January 2003

Chapter
1
FUNDAMENTALS OF CRYSTALLINE STATE
Introduction
The concepts of crystalline state and symmetry are just about
synonymous today, although the general sense of symmetry is much older
than the idea of symmetrical arrangement of atoms in the structures of
crystalline solids. Following Webster's dictionary,' symmetry is the "beauty
of form arising from balanced proportions", and to be symmetrical is to have
the "correspondence in size, shape and relative position or parts on opposite
sides of a dividing line or median plane or about a center or axis".
Humans constantly deal with symmetry, often without even noticing its
significance in daily life. For instance, our exposure to symmetry begins
every morning with a glimpse in a mirror, and it ends every night when we
fall asleep in a bed with balanced proportions.
In
addition to the fact that
intuitive perception of symmetry is familiar to almost everyone, it has
multiple applications in science and engineering.
A
much more
comprehensive and formal description of symmetry, when compared to that
found in dictionaries is, therefore, necessary.
In
this chapter, we consider basic concepts of crystallographic symmetry,
which are essential to the understanding of how atoms and molecules are
arranged in space and how they form crystalline solids. Furthermore, the
detailed knowledge of crystallographic symmetry is important to appreciate
both the capabilities and limitations of powder diffraction techniques when
they are applied to the characterization of the crystal structure of solids. We
begin with the well-established notions of the three-dimensional periodicity
'
Webster's Seventh New Collegiate Dictionary, G.
&
C.
Merriam Company Publishers,
Springfield,
MA,
USA
(1963).

2
Chapter
1
of crystal lattices and conventional crystallographic symmetry, and consider
the properties and interactions of both finite and infinite symmetry elements,
including an examination of both point and space groups.'
In
addition to the
direct crystallographic space, i.e. the physical space which is used to
represent crystal structures, we will also describe the so-called reciprocal
space, which is used to represent diffraction from crystalline solids.
The entirely formal algebraic treatment of crystallographic symmetry,
which is usually omitted in most texts, will be introduced and briefly
discussed since both the modern crystallography and powder diffraction are
for the most part computerized. Furthermore, the algebraic description of
crystallographic symmetry makes the subject complete. The chapter ends
with a brief introduction to a non-conventional crystallographic symmetry,
which has been a poignant subject in crystallography since the discovery of
perfectly ordered but clearly aperiodic crystals.
Without a doubt, it is impossible to include each and every detail about
crystallographic symmetry in this chapter, which is a part of the book about
powder diffraction. We hope, however, that after the main concepts
introduced here are understood, the reader will be ready to take on a much
more comprehensive description of crystallographic symmetry,
e.g. that
found in the International Tables for Cry~tallography.~
1.2
Crystalline state
Matter usually exists in one of the three basic states: gaseous, liquid, or
solid. At fixed temperature and pressure, only one of the states is typically
stable for any given substance, except for certain combinations of these
thermodynamic variables, where two or all three states may co-exist in
equilibrium. By decreasing temperature
and/or increasing pressure, a gas
may be condensed into a liquid and then into a solid, although in some cases
gas
e
solid transitions occur without formation of a liquid phase. The most
Finite symmetry elements and point groups are employed to describe relationships among
parts of finite objects, such as geometrical figures or shapes of natural or synthetic
crystals. Finite and infinite symmetry elements combined and space groups establish
symmetrical relationships among components of infinite objects,
e.g. two-dimensional
wall patterns or three-dimensional arrangements of atoms or molecules in structures of
crystals. Although the division of symmetry elements on finite and infinite is not in
common use, we will employ this terminology both for convenience and to emphasize the
nature of the objects (finite and infinite, respectively) they describe. Finite elements are
also known as non-translational, and the infinite ones as translational symmetry.
International Tables for Crystallography, vol. A, Fifth revised edition, Theo Hahn, Ed.
(2002); vol.
B,
Second edition,
U.
Shmueli, Ed. (2001); vol. C, Second edition, A.J.C.
Wilson and
E.
Prince, Eds. (1999). All volumes are published for the International Union
of Crystallography by Kluwer Academic Publishers,
Boston/Dordrecht/London.

Fundamentals
of
crystalline state
3
fundamental differences between gases, liquids and solids are summarized in
Table
1.1.
Gases are formed by weakly interacting, nearly isolated particles
-
atoms
or molecules. Interatomic or intermolecular distances continuously change
and as a result, gases have no fixed shape or volume and gaseous matter
occupies all available space. As far as macroscopic properties of a gas are
concerned, they remain identical in any direction because its structure, more
precisely, the absence of long- or short-range order, is isotropic.
When attraction among atoms or molecules becomes strong enough to
keep them in the immediate vicinity of each other, gas condenses into a
liquid. Since chemical bonding between particles in a liquid remains
relatively weak, thermal energy is sufficient to continuously move molecules
around and away from their nearest neighbors. When a molecule in a liquid
is removed from the assembly of nearest neighbors, another molecule
immediately occupies its place, thus preserving only short-range order.
Hence, particles in a liquid are not linked together permanently, and liquids
have specific volume but no fixed shape. Structures of liquids and, therefore,
their properties remain isotropic on a macroscopic scale.
When attractive forces among particles become so strong that they cannot
easily move away from one another, matter becomes solid. Solids have both
shape and volume. Although particles in a solid can be distributed randomly
in space, an ordered and repetitive pattern is more likely, as it corresponds to
a lower energy state when compared with a random spatial distribution of
strongly interacting atoms or molecules. The appearance of long-range order
brings about structural anisotropy and macroscopic properties of crystalline
solids become directionally dependent,
i.e. anisotropic.' It is important to
recognize that not all solids are crystalline or ordered. For example, glass has
both shape and volume but it also has a high degree of disorder, and
therefore, is classified as an amorphous solid. Lack of long-range order
makes macroscopic properties of amorphous solids isotropic.
Table
I. I.
Basic characteristics of the three states of matter.
State of matter Fixed volume Fixed shape Order Properties
Gas No No None Isotropica
Liquid Yes No short-rangeb Isotropic
Solid (amorphous) Yes Yes short-rangeb Isotropic
Solid (crystalline) Yes Yes ~ong-rangeb AnisotropicC
a
A system has same properties in all directions.
Short-range order is over a few atoms. Long-range order extends over
-lo3
to
-loz0
atoms.
A system has different properties in different directions.
'
This statement is true for single crystals, where atomic-scale anisotropy is preserved on a
macroscopic scale. Properties of polycrystals, i.e. solids that consist of a large number of
randomly oriented single crystalline grains, remain isotropic.

4
Chapter
I
One of the most distinct properties of the crystalline state is, therefore,
the presence of long-range order, or in other words, a regular and in the
simplest case periodic repetition of atoms or molecules in space.
In
theory,
periodic crystals are infinite, but in practice, their periodicity extends over a
distance from
-lo3 to -lo2' atomic or molecular dimensions, which occurs
because any crystal necessarily has a number of defects and may contain
impurities without losing its crystallinity. Furthermore, a crystal is always
finite regardless of its size.
Since our surroundings are three-dimensional, we tend to assume that
crystals are formed by periodic arrangements of atoms or molecules in three
dimensions. However, many crystals are periodic only in two, or even in one
dimension, and some do not have periodic structure at all,
e.g. solids with
incomrnensurately modulated structures, certain polymers, and quasicrystals.
Materials may assume states that are intermediate between those of a
crystalline solid and a liquid, and they are called liquid crystals. Hence, in
real crystals, periodicity
and/or order extends over a shorter or longer range,
which is a function of the nature of the material and conditions under which
it was crystallized. Structures of real crystals, e.g. imperfections, distortions,
defects and impurities, are subjects of separate disciplines, and symmetry
concepts considered below assume an ideal crystal' with perfect periodicity.'
1.3
Crystal lattice and crystal structure
Periodic structure of an ideal crystal is best described by a lattice.
In
a
lattice, all elementary parallelepipeds, i.e. unit cells, are equal in their shape
and content. If the distribution of atoms in one unit cell is known, the whole
crystal can be constructed by simply propagating (translating or shifting) this
unit cell along one, two or three directions independently.
An
example of a
simple two-dimensional lattice is shown in
Figure
I. I.
Each unit cell, one of
which is shaded, is the parallelogram delineated by solid lines, and every
unit cell contains one hypothetical molecule that consists of three atoms: one
large, one medium, and one small. The structure of this molecule, including
bond lengths and bond angle, remains identical throughout the whole lattice.
Diffraction by an ideal mosaic crystal is best described by a kinematical theory of
diffraction, whereas diffraction by an ideal crystal is dynamical and can be described by a
much more complex theory of dynamical diffraction. The latter is used in electron
diffraction, where kinematical theory does not apply. X-ray diffraction by an ideal mosaic
crystal is kinematical, and therefore, this relatively simple theory is used in this book. The
word "mosaic" describes a crystal that consists of many small, ideally ordered blocks,
which are slightly misaligned with respect to one another. "Ideal mosaic" means that all
blocks have the same size and degree of misalignment with respect to other mosaic blocks.
'
Most of this chapter is dedicated to conventional crystallographic symmetry, where three-
dimensional periodicity is implicitly assumed.
Fundamentals
of
crystalline state
5
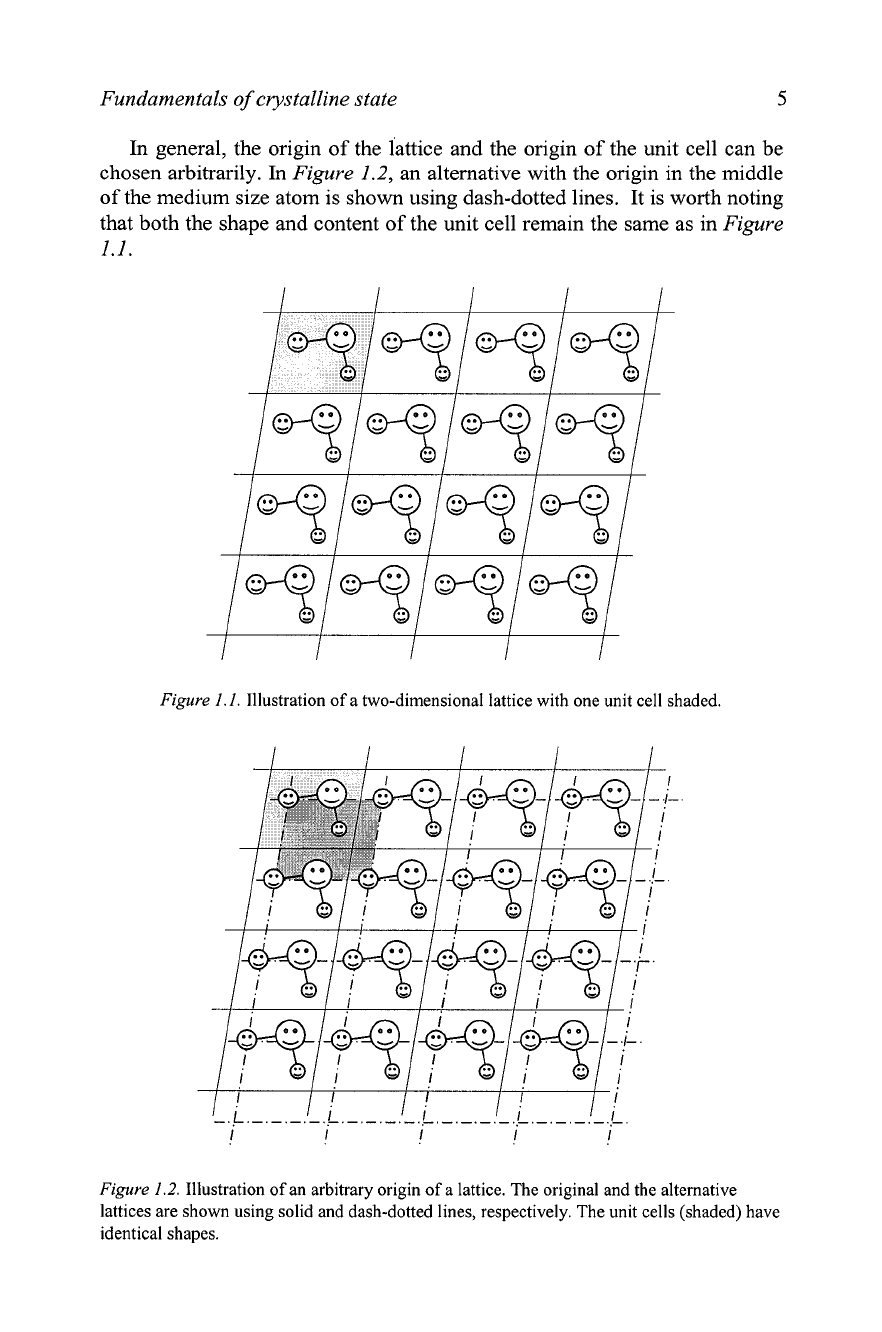
In general, the origin of the lattice and the origin of the unit cell can be
chosen arbitrarily. In
Figure
1.2,
an alternative with the origin in the middle
of the medium size atom is shown using dash-dotted lines. It is worth noting
that both the shape and content of the unit cell remain the same as in
Figure
1.1.
Figure
I. I.
Illustration of a two-dimensional lattice with one unit cell shaded.
Figure
1.2.
Illustration of an arbitrary origin of a lattice. The original and the alternative
lattices are shown using solid and dash-dotted lines, respectively. The unit cells (shaded) have
identical shapes.
Chapter
I
Figure
1.3.
Illustration of an arbitrary unit cell of a lattice. The original and the alternative
lattices are shown using solid and dash-dotted lines, respectively. The unit cells (shaded) have
different shapes but their areas (volumes in three dimensions) remain identical.
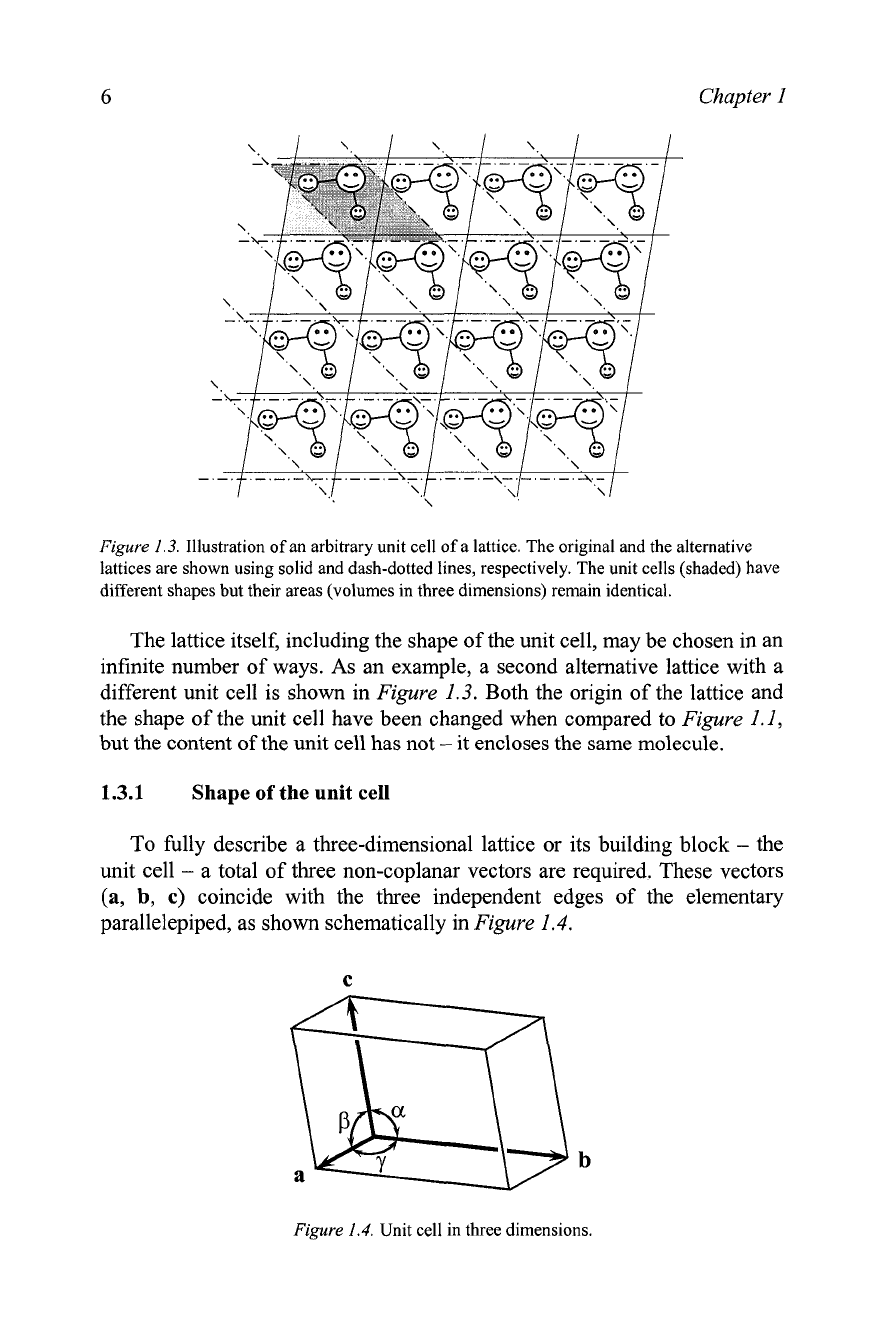
The lattice itself, including the shape of the unit cell, may be chosen in an
infinite number of ways. As an example, a second alternative lattice with a
different unit cell is shown in
Figure
1.3. Both the origin of the lattice and
the shape of the unit cell have been changed when compared to
Figure
1.1,
but the content of the unit cell has not
-
it encloses the same molecule.
1.3.1
Shape
of
the unit cell
To fully describe a three-dimensional lattice or its building block
-
the
unit cell
-
a total of three non-coplanar vectors are required. These vectors
(a,
b,
c)
coincide with the three independent edges of the elementary
parallelepiped, as shown schematically in
Figure
1.4.
Figure
1.4.
Unit cell in three dimensions.

Fundamentals
of
crystalline state
7
Therefore, any point in a three-dimensional lattice can be described by a
vector,
q,
defined in
Eq.
1.1,
where
u,
v,
and
w
are integer numbers
The three basis vectors (a, b, c) and all derived vectors (q) represent
translations in the lattice. They translate the unit cell, including every atom
and/or molecule located inside the unit cell, in three dimensions, thus filling
the entire space of a crystal. The unit cell can be completely described by
specifying a total of six scalar quantities, which are called the unit cell
dimensions or lattice parameters. These are (see also Figure
1.4):
The first three parameters (a, b and c) represent the lengths of the unit
cell edges, and the last three
(a,
p
and y) represent the angles between them.
Thus,
a
is the angle between b and c,
P
is the angle between a and c, and y is
the angle between a and b.
Unit cell dimensions are usually quoted in angstroms (A, where 1
=
10-lo m
=
cm), nanometers (nm, 1 nm
=
m), or picometers (pm,
1
pm
=
10''~ m) for the lengths of the unit cell edges, and in degrees
(")
for the
angles between basis vectors. To differentiate between basis vectors (a, b,
c),
which appear in bold, the lengths of the unit cell edges (a, b, c) always
appear in italic.
1.3.2
Content of the unit
cell
To completely describe the crystal structure, it is not enough to
characterize only the geometry of the unit cell. One also needs to establish
the distribution of atoms in the unit cell and in the lattice. The latter is done
simply by translating each point in space using Eq. 1.1. Hence, the three
non-coplanar vectors
a,
b and c form a basis of the coordinate system with
three non-coplanar axes
X,
Y
and Z, which is called the crystallographic
coordinate system or the crystallographic basis. The coordinates of a point
inside the unit cell, i.e. the coordinate triplets x,
y,
z, are expressed in
fractions of the unit cell edge lengths and they vary from 0 to 1 along the
corresponding vectors (a, b or c). Thus, the coordinates of the origin of the
unit cell are always 0, 0, 0
(x
=
0,
y
=
0 and
z
=
O), and for the ends of X-,
Y-, and Z-axes, they are 1,0, 0; 0, 1, 0 and 0, 0,
1,
respectively. Again, using
capital italic X,
Y
and Z, we will always refer to crystallographic axes
coinciding with a, b and c, respectively, while small italic x,
y
and z will be
used to specify the corresponding fractional coordinates along
X,
Y
and Z.

Chapter
1
Figure
1.5.
Illustration of the content of the unit cell. The coordinates of the center of each
atom are given as doublets, i.e.
xl, yl; x2, yz
and
x3, y3.
In three dimensions, they become
triplets, i.e.
xi,
yi,
zi.
An
example of the unit cell in two dimensions and its content in terms of
coordinates of all atoms is shown in
Figure
1.5.
Here, the three atoms
("large", "medium", and "small") have coordinates x,,
y,;
x2,
y2
and x3,
y3,
respectively. Strictly speaking, the content of the unit cell should be
described by specifying other relevant atomic parameters in addition to the
position of each atom in the unit cell. These include types of atoms
(i.e. their
chemical symbols or sequential numbers in a periodic table instead of "big",
"medium" and "small"), site occupancy and individual displacement
parameters. All of these terms will be defined and explained later in this
book.
1.3.3
Asymmetric part
of
the unit cell
It is important to realize that the case shown in
Figure
1.5
is rarely
observed in reality. Usually, unit cell contains more than one molecule or a
group of atoms that are converted into each other by simple geometrical
transformations, which are called symmetry operations. There may be as
many as
192
transformations total in some highly symmetric unit cells. One
example is shown in
Figure
1.6,
where each unit cell contains two molecules
that are converted into one another by
180'
rotation around imaginary lines,
which are perpendicular to the plane of the figure. The location of one of
these lines (rotation axes) is indicated using small filled ellipse. The original
molecule, chosen arbitrary, is white, while the derived molecule is shaded.
The independent part of the unit cell (e.g. the upper right half of the unit
cell separated by a dash-dotted line and shaded in
Figure
1.6)
is called the
asymmetric unit. It is the only part of the unit cell, for which the
specification of atomic positions and other atomic parameters are required.

Fundamentals
of
crystalline state
9
The entire content of the unit cell can be established from its asymmetric
unit using the combination of symmetry operations present in the unit cell.
Here, this operation is a rotation by
180'
around the line perpendicular to the
plane of the projection at the center of the unit cell. It is worth noting that
the rotation axis shown in the upper left comer of
Figure
1.6
is not the only
axis present in this crystal lattice
-
identical axes are found at the beginning
and in the middle of every unit cell edge as shown in one of the neighboring
ce1ls.l
Symmetry operations, therefore, can be visualized by means of certain
symmetry elements represented by various graphical objects. There are four
so-called simple symmetry elements: a point to visualize inversion, a line for
rotation, a plane for reflection and the already mentioned translation is also a
simple symmetry element, which can be visualized as a vector. Simple
symmetry elements may be combined with one another producing complex
symmetry elements that include roto-inversion axes, screw axes and glide
planes.
Figure
1.6.
Asymmetric unit (shaded) containing an independent molecule, which is clear.
Shaded molecules are related to clear molecules in each unit cell
via
rotation by
180"
around
the lines perpendicular to the plane of the projection at the center of each unit cell. All
rotation axes are shown in a neighboring cell.
'
The appearance of additional rotation axes in each unit cell is the result of the
simultaneous presence of both rotational and translational symmetry, which interact with
one another (see sections
1.6
and
1.13.3,
below).
